采用VSG 策略的MMC 阻抗建模及并網穩定性分析

孫 杰，尹太元，王 躍，劉 普，王曉雷，樂 波

（1.西安交通大學電氣工程學院，西安 710049；2.鄭州輕工業大學電氣與信息工程學院，鄭州 450000；3.中原工學院電子信息學院，鄭州 450007；4.國網經濟技術研究院有限公司，北京 102209）

模塊化多電平換流器MMC（modular multi-level converter）由于其模塊化、開關頻率低、輸出電壓波形畸變小等優點，逐漸成為柔性直流輸電系統中廣泛采用的換流器[1-3]。近年來，分布式能源大規模并網，電網的慣性和調節能力隨著分布式能源的高滲透率而降低[4]，虛擬同步發電機VSG（virtual syn-chronous generator）控制技術由于具有類似同步發電機的調頻和調壓能力，并能夠為系統提供一定的慣性和阻尼支撐等優點，為解決新能源大規模并網所帶來的穩定性問題提供了新的解決方案，逐漸得到國內外學者的高度重視和廣泛研究[5-6]。

基于端口阻抗的穩定性分析法是目前被學術界和工業界廣泛采用的穩定性分析方法，多個柔直工程均采用了此方法，并且其準確性和有效性也得到了充分的驗證[7-9]。目前采用VSG 控制策略的并網逆變器的阻抗建模多集中在兩電平換流器，文獻[10-11]研究了電壓型VSG 和電流型VSG 的小信號阻抗建模及其與弱電網的交互穩定性。而MMC 由于內部動態特性復雜，在子模塊電容電壓和橋臂電流中含有很多諧波，且不同諧波之間存在復雜的耦合關系[12-15]，相較于VSC 的阻抗建模要復雜得多，且其阻抗模型跟VSC 有較大差別。文獻[16]首次基于諧波線性化的建模方法建立了包含環流抑制和鎖相環的單電流環MMC 整流器的阻抗模型。文獻[17]基于諧波狀態空間法建立了MMC 交流側阻抗，分析了級聯系統的穩定性。文獻[18]對具有完整控制環路的MMC-HVDC 系統進行了序阻抗建模并進行了穩定性分析。

但是上述文獻均未涉及VSG 控制策略下的MMC 阻抗建模，其端口阻抗特性尚不明確，也鮮有基于阻抗分析法對采用VSG 控制策略的MMC 進行并網穩定性研究，而由于VSG 控制策略的MMC在接入弱電網時對電網具有慣性和阻尼支撐的優點，未來在柔直領域中有廣闊的應用前景，因而十分有必要建立其阻抗模型，并研究其與弱電網交互時的穩定性問題，這對基于MMC 拓撲在不同控制模式下的阻抗模型和在柔直工程中的穩定性研究是一項重要補充，能夠為其并網安全運行提供理論依據，并對其參數設計提供理論指導。

本文首先研究MMC 的VSG 控制策略，然后基于諧波線性化方法詳細推導VSG 控制策略下的MMC 阻抗模型，并進行驗證。然后根據得到的MMC 阻抗伯德圖，分析其阻抗特性，研究VSG 控制參數對MMC 阻抗特性的影響以及VSG 控制策略下MMC 的阻抗靈敏度。再結合電網阻抗特性，并根據奈奎斯特穩定判據分析在弱電網條件下VSG控制策略下MMC 的并網穩定性。最后通過實驗驗證上述穩定性分析的正確性，本文研究結果可為采用VSG 控制策略的MMC 并網系統的控制和穩定性分析以及穩定性優化提供參考。

1 MMC 拓撲及其VSG 控制策略

MMC 的結構框圖如圖1 所示。其由6 個三相橋臂組成，每相上下2 個橋臂完全相同，每個橋臂由N 個半橋子模塊和1 個橋臂電感L 組成，L 的等效寄生電感為rL。圖1 中，vj（j=a，b，c）為MMC 交流端口電壓，ij（j=a，b，c）為MMC 交流端口電流，iju（j=a，b，c）為流過三相上橋臂的電流，ijl（j=a，b，c）為流過三相下橋臂的電流，Udc為MMC 直流側電壓。通過控制橋臂子模塊投入的數量改變交流端口電壓，橋臂電感L 可以抑制相間環流并減少內部電流的諧波含量。

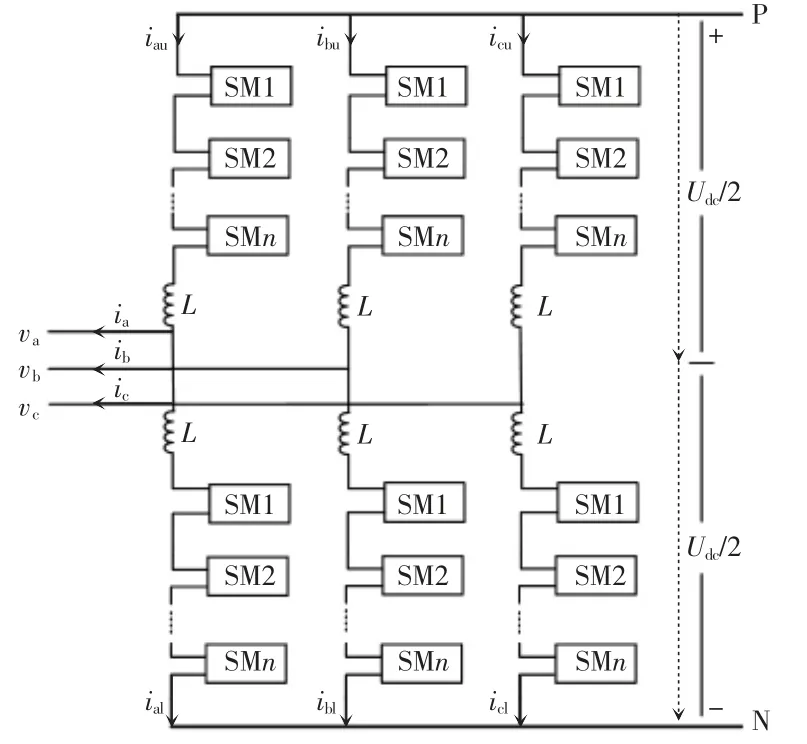
圖1 MMC 的結構框圖Fig.1 Structural diagram of MMC

圖2 為包含環流抑制環節的VSG 控制框圖，包括功率計算部分、功率控制部分和環流抑制部分。功率計算部分及功率控制部分主要是為了模擬同步發電機的特性，其又分為有功-頻率控制和無功-電壓控制。有功-頻率控制主要是為了模擬同步發電機的一次調頻特性和轉子慣性；無功-電壓控制是為了模擬電壓調節特性。

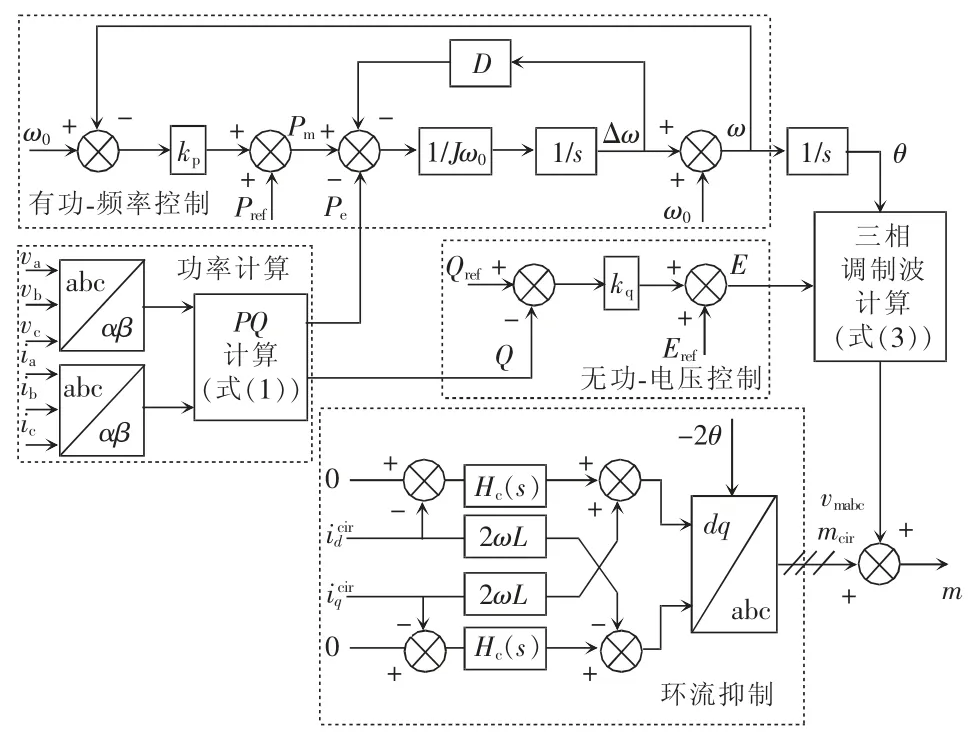
圖2 VSG 控制框圖Fig.2 Block diagram of VSG control

VSG 輸出有功功率Pe和輸出無功功率Q 由瞬時功率理論計算，其計算公式為

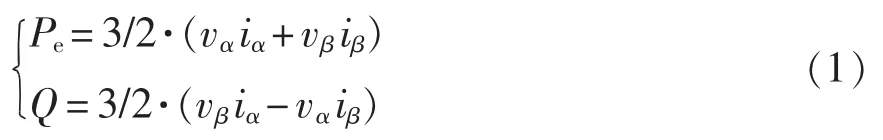
式中：vα、vβ為由三相輸出電壓經Clark 變換得到的輸出電壓；iα、iβ為由三相輸出電流經Clark 變換得到的輸出電流。

VSG 有功控制器的數學方程為

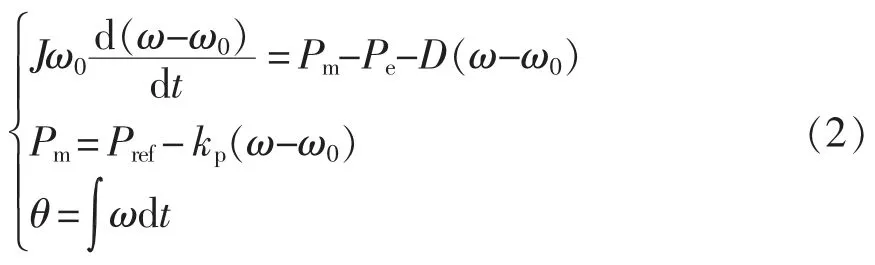
式中：J 為虛擬轉動慣量；ω0為電網的額定角頻率；ω 為VSG 有功控制環路的輸出角頻率；Pm為虛擬機械功率；Pe為電磁功率；D 為阻尼系數；Pref為有功功率指令；kp為有功-頻率下垂系數；θ 為VSG 輸出角度。

VSG 無功控制器的數學方程為

式中：E 為虛擬內電勢的峰值；Eref為內電勢峰值指令；Qref為無功功率指令；Q 為輸出無功功率；kq為無功-電壓下垂系數。

VSG 的有功-頻率控制器和無功-電壓控制器的輸出共同決定其產生的調制波，數學方程為

式中，vma、vmb、vmc為VSG 生成的調制波。

環流抑制控制器生成的調制波為mcir，將其與vmabc疊加，即可得到MMC 的調制波信號m。

2 VSG 控制策略的MMC 阻抗建模

諧波線性化是一種獲取換流器阻抗的簡便方法，其應用范圍比較廣。相比于傳統dq 坐標系中的建模，諧波線性化的穩態運行軌跡可以包含任意數量的諧波，計算出來的阻抗有清晰的物理解釋并可以直接測量[19]。下面基于諧波線性化思想對基于VSG控制策略下的MMC 進行阻抗建模。

2.1 MMC 電氣系統小信號模型

基于諧波線性化的阻抗建模首先需要在MMC交流側注入頻率為fp的擾動電壓，以a 相為例，加入擾動電壓之后的a 相端口電壓va（t）為

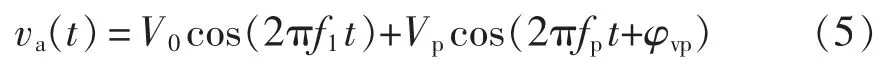
式中：V0為a 相電網電壓的幅值；f1為a 相電網電壓的頻率；Vp為在MMC 交流端口注入的擾動電壓幅值；φvp為其初相位，對于b 相和c 相，只須根據注入擾動信號的正負序將相位在a 相相位的基礎上超前或滯后2π/3 即可。

MMC 由于子模塊數目很多，等效開關頻率極高，可以認為所有子模塊電容電壓始終保持均衡[20]，根據MMC 的對稱性，以a 相上橋臂為例，可以得到MMC 的功率級小信號模型[16]為

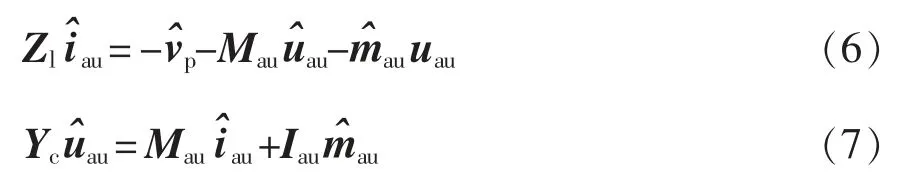
對于給定頻率為fp的電壓擾動將會導致系統產生一系列頻率為fp±kf1（k=1，2，…，n）的小信號諧波分量，雖然理論上會產生無限多頻次的諧波，但這些諧波的幅值會隨著k 的增加而減小[21-22]，考慮數學運算的復雜性和阻抗建模精度的要求，通常只須考慮3 次以內的諧波即可,表1 給出了各頻次諧波正負序和差模共模的信息[16]。

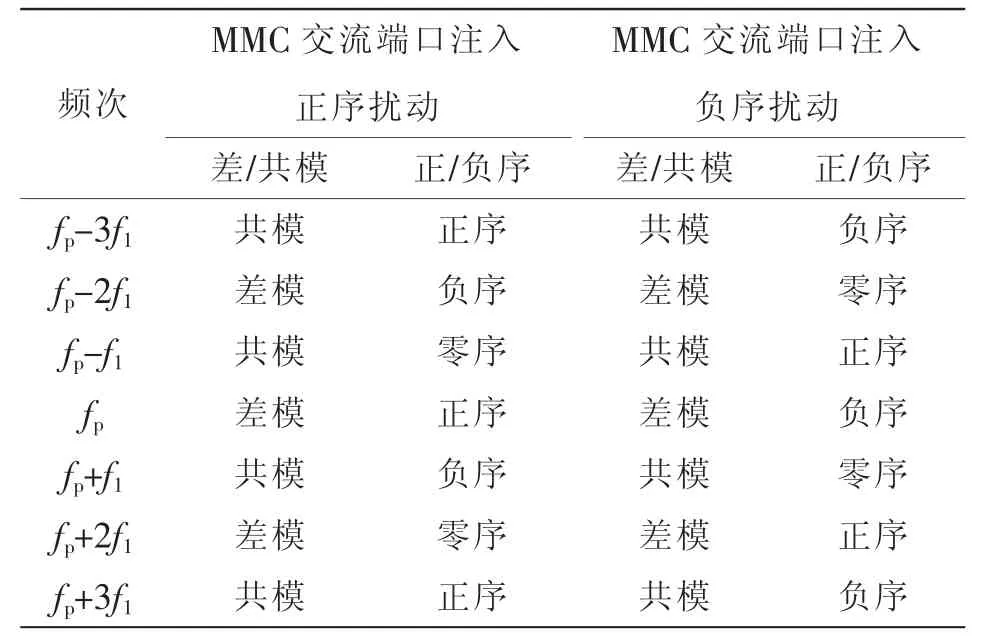
表1 小信號諧波之間的關系Tab.1 Relationship among small-signal harmonics

2.2 MMC 控制部分的小信號模型

根據式（6）和式（7）可以看出，Iau、uau和Mau是穩態量，可以從MMC 輸出功率計算得到，可以消掉，此時如果能用和表示，那么就可以通過計算和的比值進而得到MMC 的阻抗。下面對MMC 交流端口注入正序小擾動電壓時的阻抗進行詳細推導，MMC 交流端口注入負序電壓擾動時的推導過程與正序時類似，本文不再贅述。

在MMC 交流端口注入fp頻次的擾動電壓，所產生的小信號電流響應中只有差模量會流到交流端口，根據表1 中的正負序和差模共模關系，對于正序電壓擾動而言，其產生的差模量的頻次分別為fp和fp-2f1頻次，分別為差模正序信號和差模負序信號，其三相表達式為

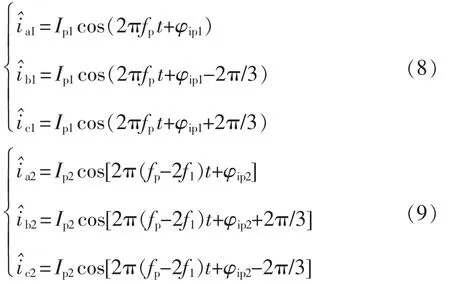
對式（8）和式（9）進行Clark 變換，將小擾動電壓和2 個頻次的小信號電流轉換到αβ 坐標系下，Clark變換矩陣Tαβ和變換后小信號電壓、電流分別為

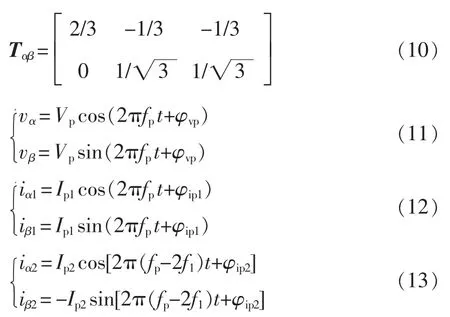
設V0和I0為穩態電壓和電流的幅值，Vα和Vβ為αβ 坐標系下MMC 的穩態電壓，Iα和Iβ為αβ 坐標系下MMC 的穩態電流，表達式分別為

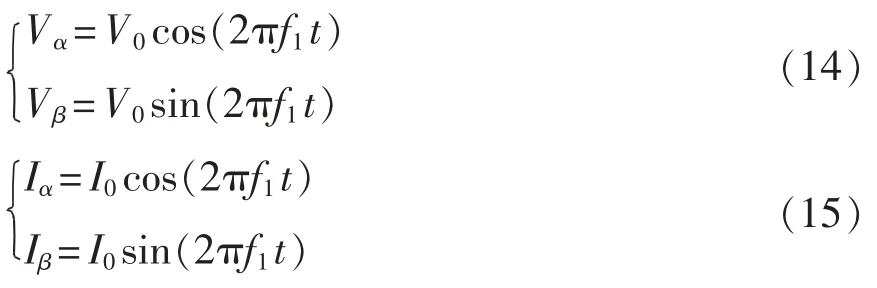
對于VSG 功率控制環路，無功控制環的輸出電壓可視為定值[23]，根據式（1）可以得到小信號形式的有功功率為

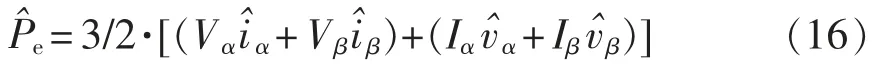
由式（16）可以看出，小信號有功功率中包含小信號電壓和2 個頻次小信號電流的影響，因此小信號有功功率可以分為3 部分，其中，對于fp頻次電流部分為

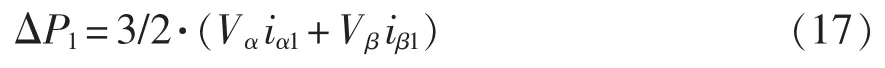
對于fp-2f1頻次電流部分為

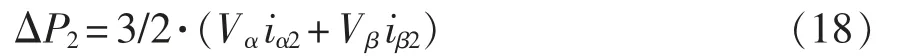
對于fp頻次電壓部分為

由圖2 所示的VSG 控制框圖可得VSG 控制部分的傳遞函數M（s）為

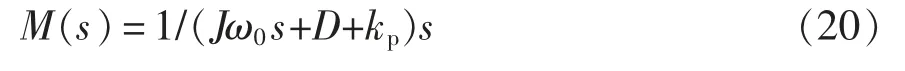
M（s）代表了從電磁功率Pe經有功-頻率控制環節得到頻率后，再積分成角度θ 的傳遞函數。

燃氣企業因為受到自身特性的影響，在開展財務信息化建設工作時，根據需要可以將不同地點、區域具有共性較強的、重復率高的、易于標準化和流程化的財務業務或職能從分、子公司中剝離出來，之后將其融合到信息平臺中，實現信息傳遞和共享。只有這樣，才能將規模效應以及協同效應充分發揮，減少財務運行成本，提升財務運營效率以及服務質量，從而降低財務運行風險，給燃氣企業的健康發展營造良好的條件。

VSG 控制環路輸出的小信號相角為

此時在VSG 輸出的三相調制波相角中引入了相角擾動Δθ。假設沒有擾動時的相角為θ0，則有

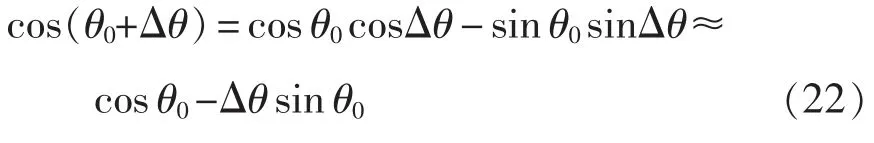
將式（21）、式（22）代入式（4）中并忽略大信號項，可以得到VSG 控制環路生成的小信號調制波為

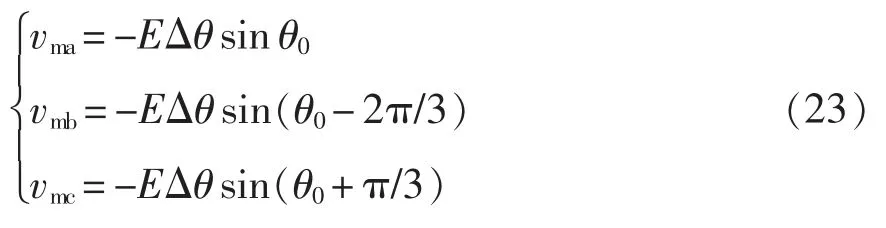
綜上并利用三角函數積化和差化簡，由fp頻次電流所影響產生的a 相小信號調制波為

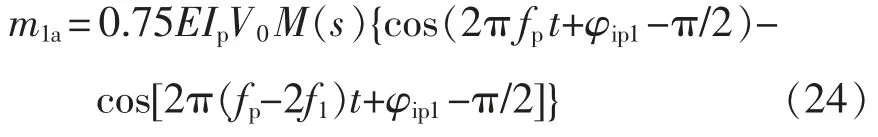
結合式（8）和式（24）可以看出，fp頻次的小信號電流在調制波中產生fp和fp-2f1兩個頻次的諧波，且與原來的小信號電流相比均有π/2 的相位延遲。因此，fp頻次的小信號電流對VSG 控制環路生成調制波的系數矩陣表示為

同理，fp-2f1頻次的小信號電流對VSG 控制環路生成調制波的系數矩陣表示為

其中

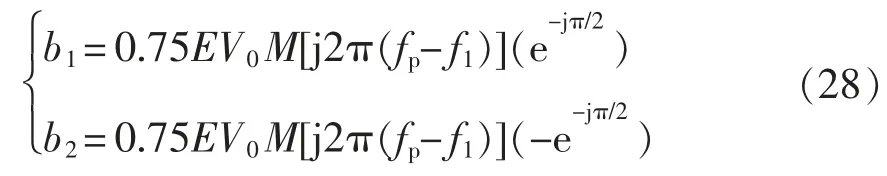
因此，VSG 控制環路中小信號電流對調制波的系數矩陣表示為

fp頻次的小信號電壓對VSG 控制回路生成調制波的系數矩陣表示為

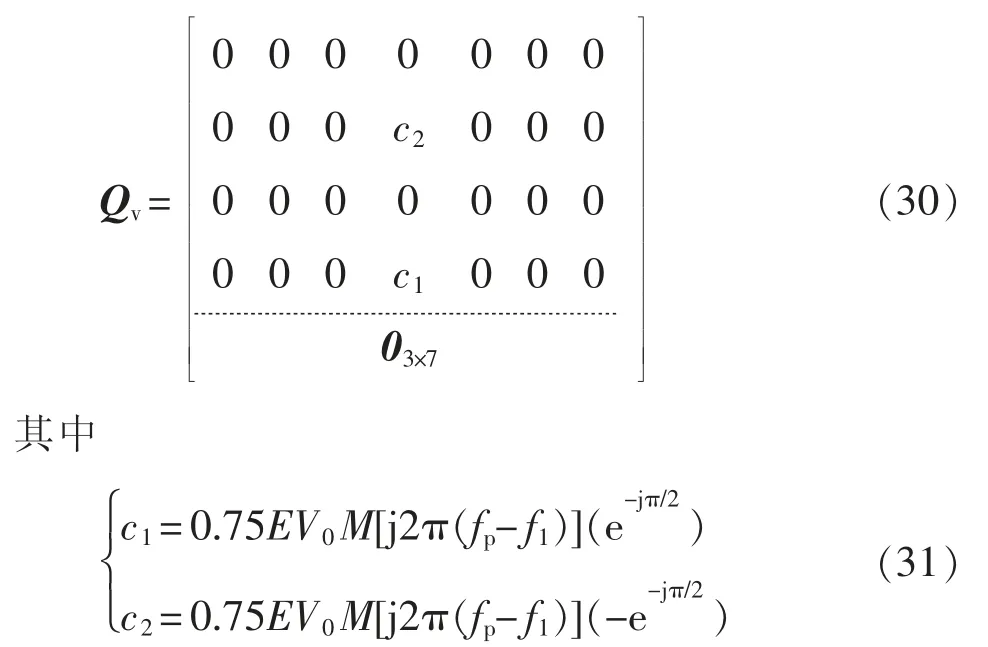
環流抑制環對調制波的系數矩陣可以表示為[10]

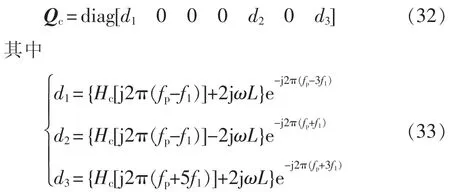
式中，Hc為環流抑制環的傳遞函數。

2.3 MMC 阻抗模型的仿真驗證

各控制環路調制波的影響可以表示為

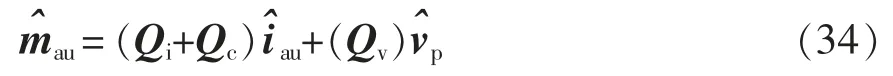
將式（34）代入式（6）和式（7），可得到小擾動電壓與橋臂小信號電流的關系為

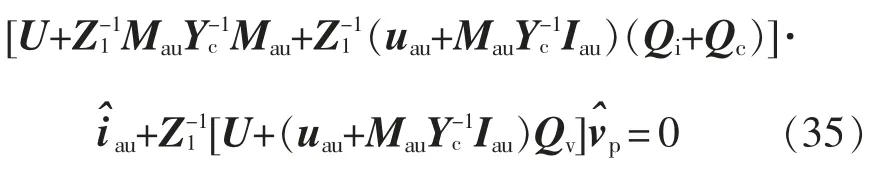
式中，U 為7 階單位矩陣。

由此可得小擾動電壓與橋臂小信號電流的7階導納矩陣為

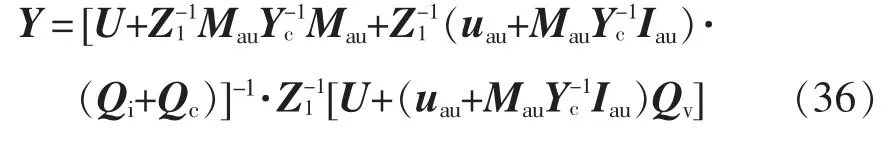
由于fp頻次的相電流是橋臂電流的2 倍[16]，因此MMC 在fp頻次的阻抗模型為

為了驗證上述建立阻抗模型的正確性，在Matlab/Simulink 中搭建仿真模型，模型參數如表2所示，通過頻率掃描法獲取仿真阻抗幅頻特性和相頻特性并與阻抗模型的解析值進行對比驗證。

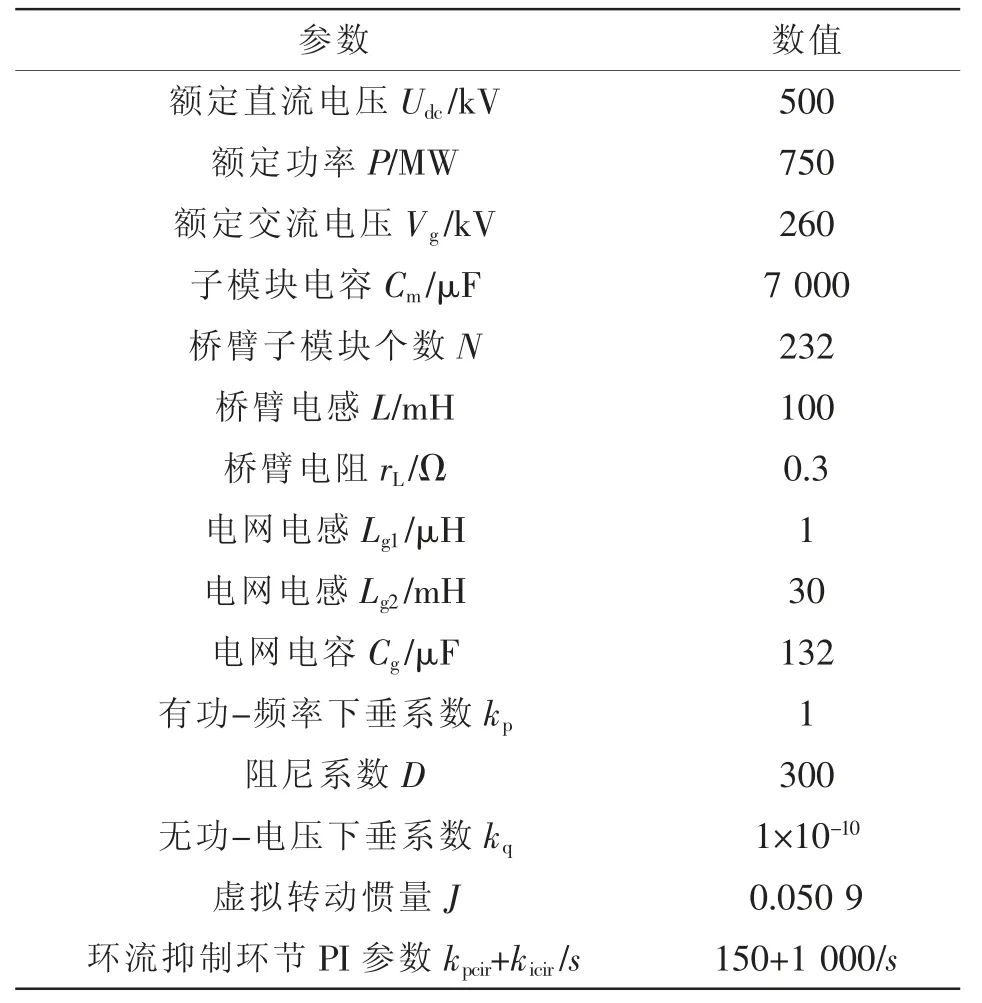
表2 MMC 的系統和控制參數Tab.2 System and control parameters of MMC

MMC 阻抗模型掃頻值與解析值對比結果如圖3 所示。由圖3 可見，解析值與掃頻值吻合，驗證了上述所建立阻抗模型的正確性。

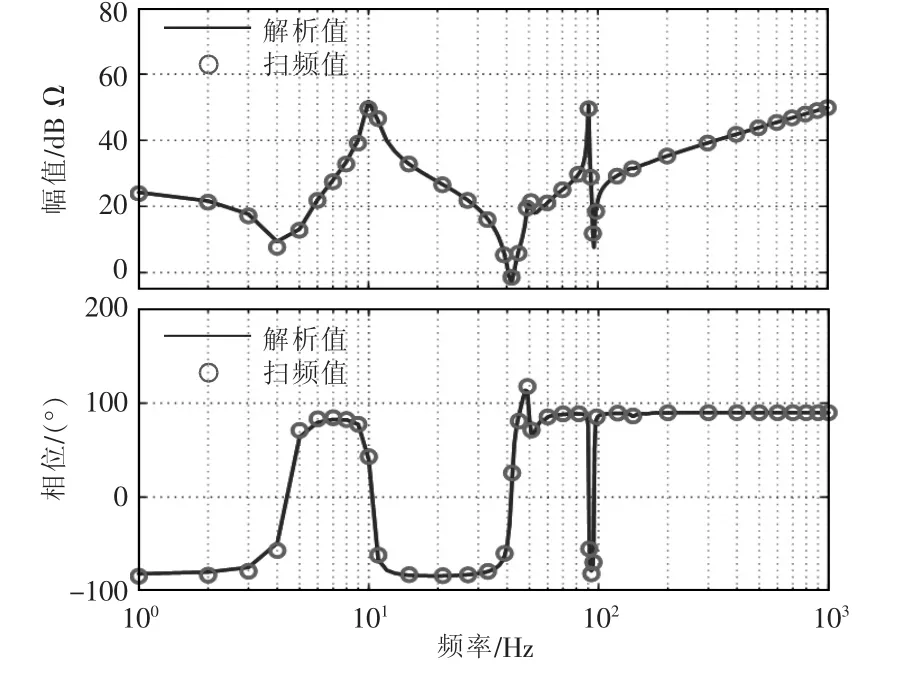
圖3 MMC 阻抗掃頻值與解析值對比結果Fig.3 Results of comparison between frequency scanning and analytical values of MMC impedance

3 MMC 并網穩定性分析

3.1 VSG 控制參數對MMC 阻抗的影響

3.1.1 控制參數對阻抗曲線的影響

有功-頻率下垂系數kp對MMC 阻抗的影響如圖4 所示，對比3 組參數（kp=1，10，100）得到的阻抗曲線，kp增大會使50 Hz 附近的2 個阻抗尖峰變小，而其他頻段的阻抗特性幾乎沒有變化，說明kp的改變對其他頻段的阻抗特性影響不大。

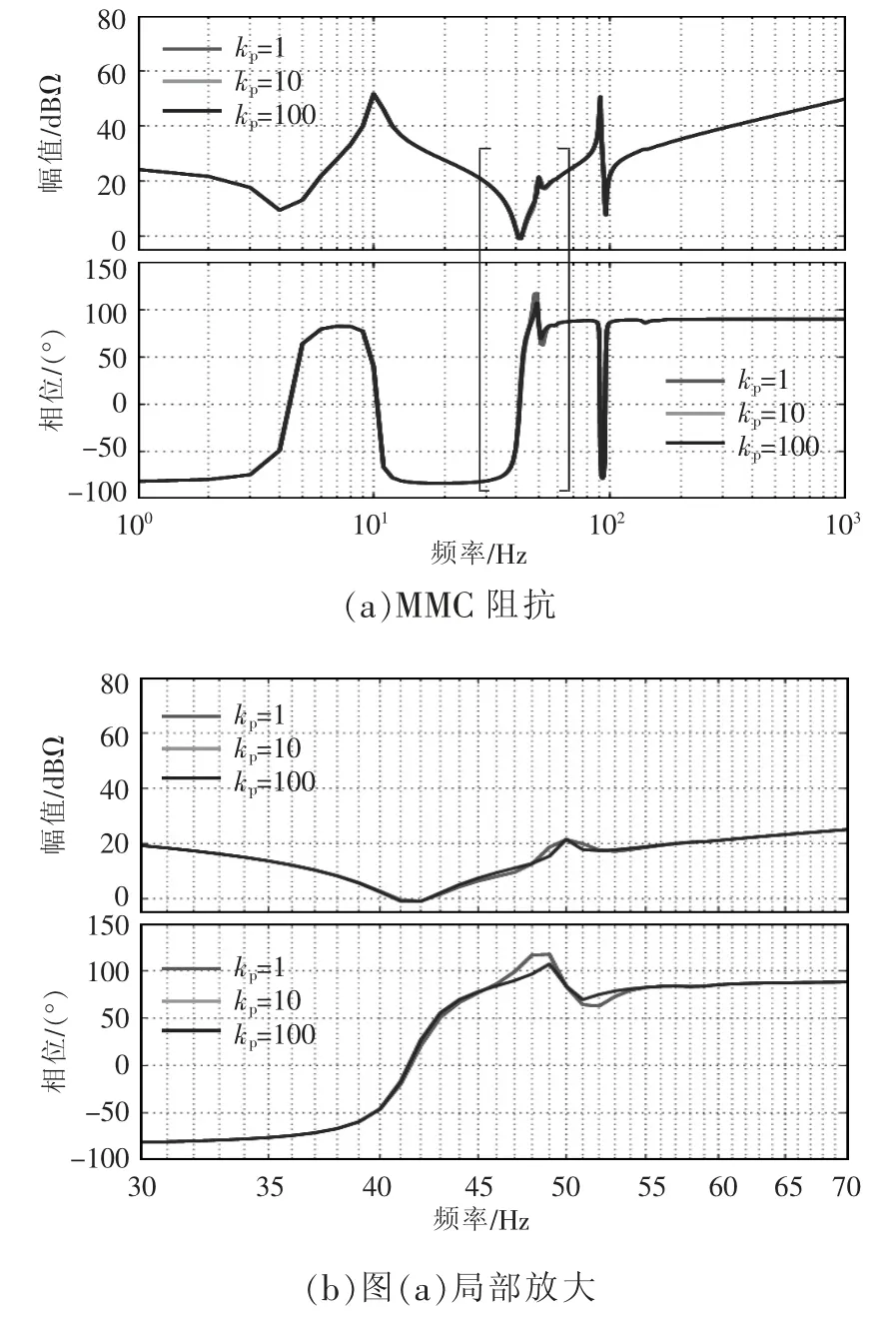
圖4 kp=1、10、100 時的MMC 阻抗Fig.4 Impedance of MMC when kp equals 1,10 and 100,respectively

阻尼系數D 對MMC 阻抗的影響如圖5 所示，從3 組不同的參數（D=200，300，400）得到的阻抗曲線可以看出，阻尼系數對MMC 阻抗的影響主要在45～55 Hz，阻尼系數越大，50 Hz 附近的2 個尖峰越小，系統阻尼越強。而其他頻段的阻抗特性幾乎沒有變化，說明D 的改變對其他頻段的阻抗特性影響不大。

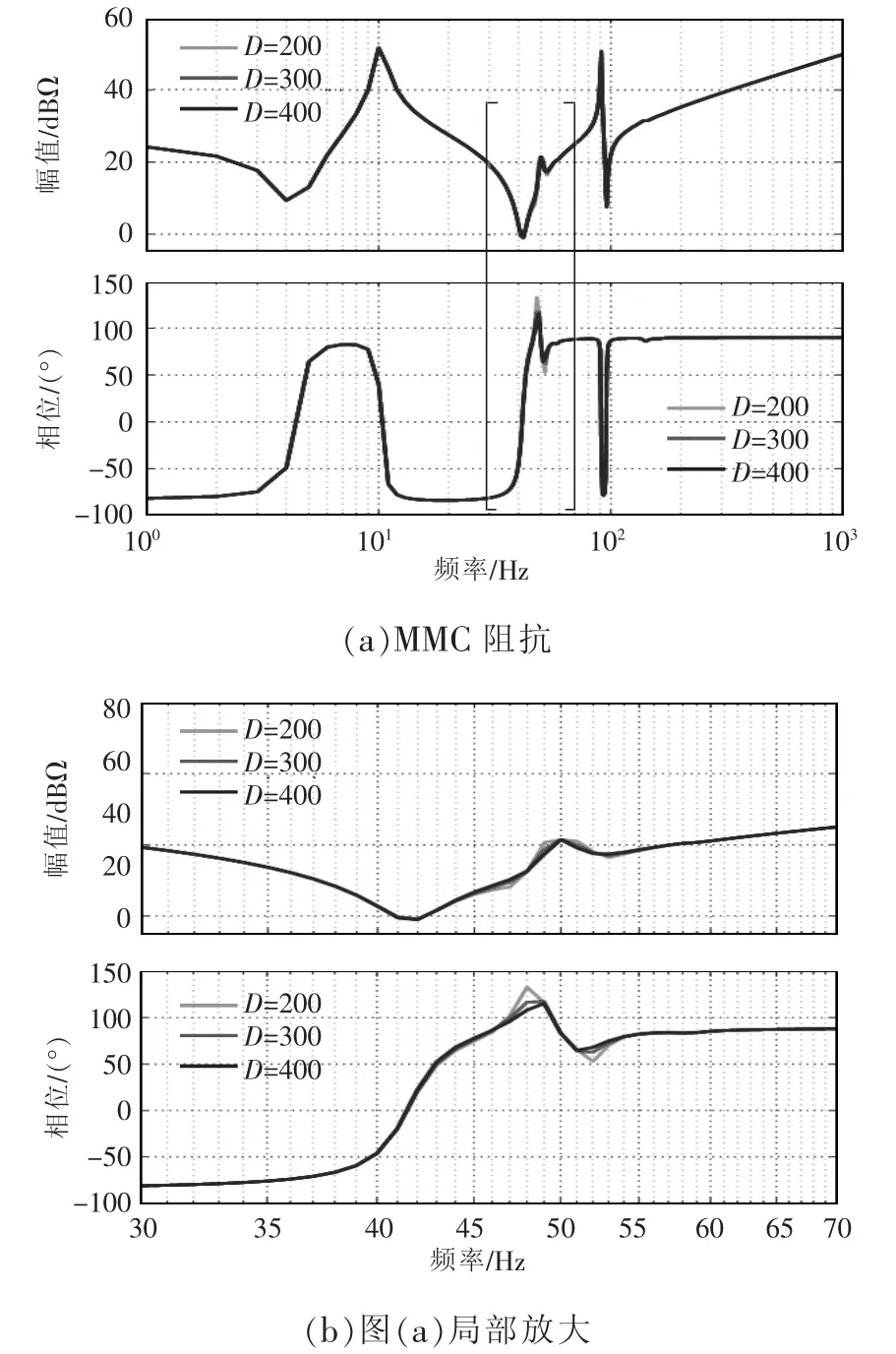
圖5 D=200、300、400 時的MMC 阻抗Fig.5 Impedance of MMC when D equals 200,300 and 400,respectively

虛擬轉動慣量J 對MMC 阻抗的影響如圖6 所示，從3 組不同的參數（J=0.025 4,0.050 9,0.102 0）得到的阻抗曲線可以看出，虛擬轉動慣量對MMC阻抗的影響主要在40～55 Hz。而其他頻段的阻抗特性幾乎沒有變化，說明J 的改變對其他頻段的阻抗特性影響不大。

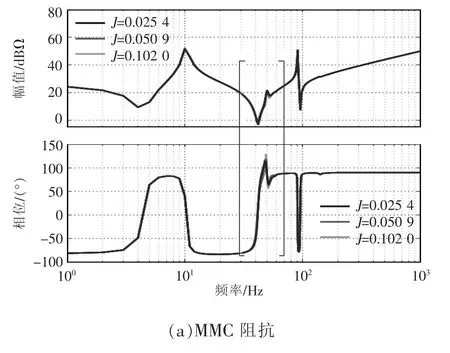
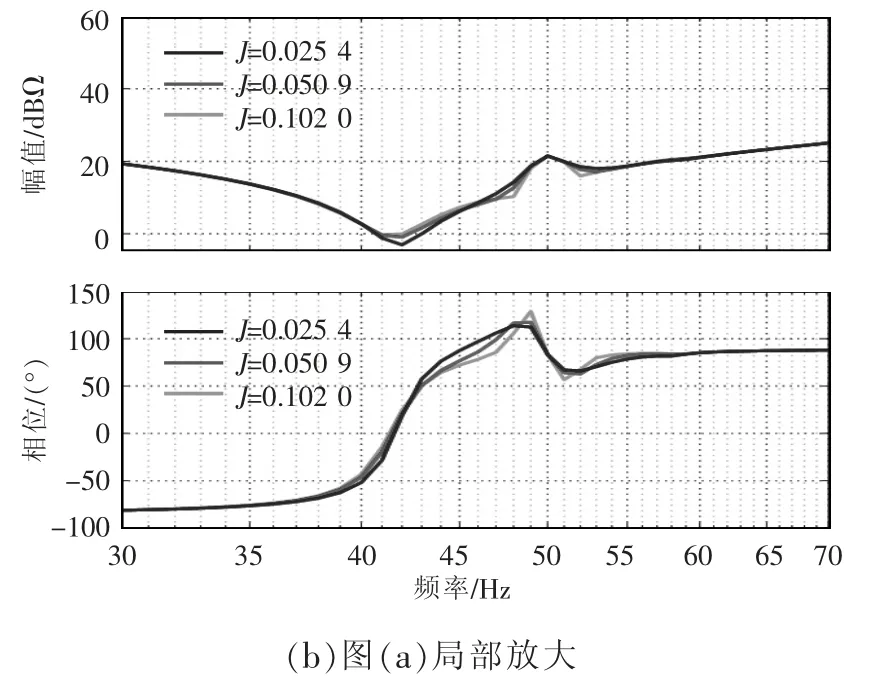
圖6 J=0.025 4、0.050 9、0.102 0 時的MMC 阻抗Fig.6 Impedance of MMC when J equals 0.025 4,0.050 9 and 0.102 0,respectively

3.1.2 控制參數的阻抗靈敏度分析

控制參數的阻抗靈敏度能夠反映當控制器不同控制參數變化時對換流器端口阻抗特性的影響大小，當一個控制參數在某個頻段得到的靈敏度值越大，說明該控制參數在該頻段對換流器阻抗特性的影響越大，也即阻抗特性在此頻段對該參數的變化越敏感；反之，當一個控制參數在某個頻段得到的靈敏度值越小時，說明該控制參數在該頻段對換流器阻抗特性的影響越小，也即阻抗特性在此頻段對該參數的變化越不敏感。控制參數的阻抗靈敏度包括阻抗幅值靈敏度和阻抗相角靈敏度，定義為

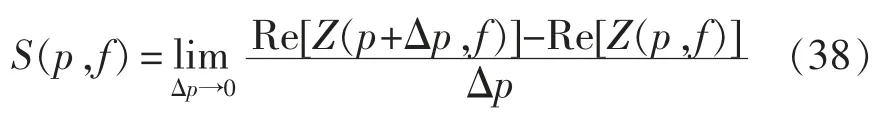
式中：p 為原本控制參數；Δp 為控制參數變化量；S為控制參數阻抗靈敏度。

有功-頻率下垂系數kp的阻抗靈敏度如圖7 所示，可見，在頻率為47、49、51 Hz 時幅值靈敏度曲線較高，說明在這3 個頻率附近的阻抗幅值對kp的變化比較敏感，而1～36 Hz、60～1 000 Hz 頻段的阻抗幅值靈敏度曲線幾乎與橫軸重合，說明在這些頻段kp的變化不會使阻抗幅值產生明顯變化；在頻率為42、48、52 Hz 時相角靈敏度較高，說明在這3 個頻率附近的阻抗相角對kp的變化比較敏感；而1～40 Hz、54～1 000 Hz 頻段的阻抗相角靈敏度曲線幾乎與橫軸重合，說明在這些頻段kp的變化不會使阻抗相角產生明顯變化。上述分析與kp變化時阻抗曲線發生變化的頻段一致。

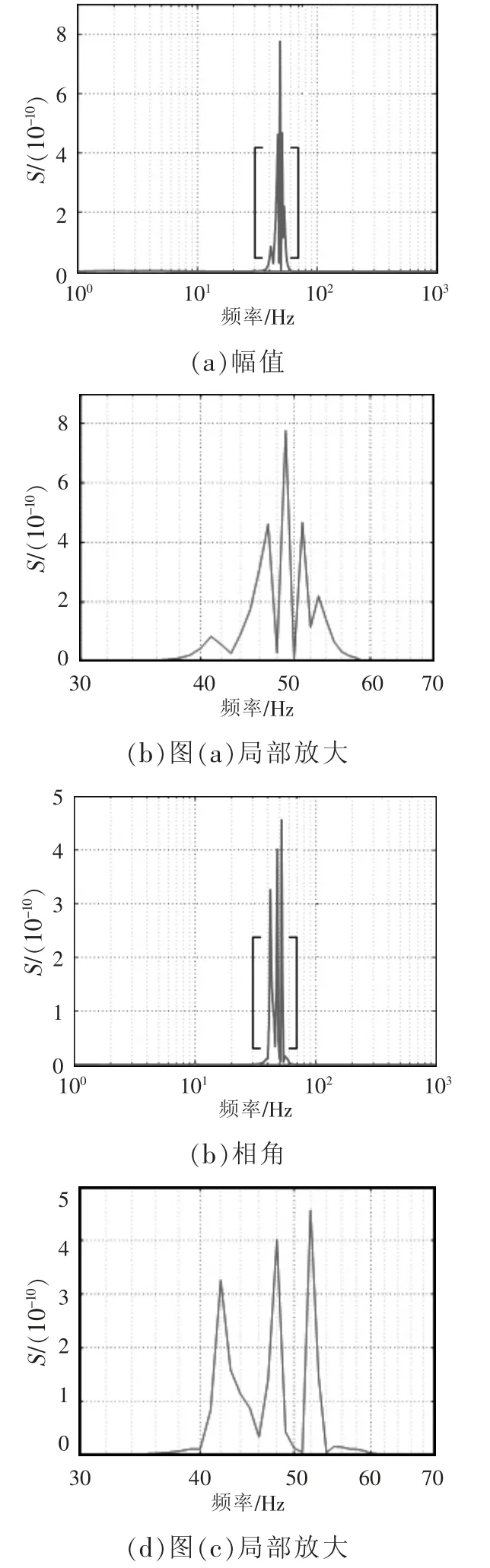
圖7 kp 的阻抗靈敏度Fig.7 Impedance sensitivity of kp

阻尼系數D 的阻抗靈敏度如圖8 所示，在頻率為47、49、51 Hz 時幅值靈敏度曲線較高，說明在這3 個頻率附近的阻抗幅值對D 的變化比較敏感；而1～36 Hz、60～1 000 Hz 頻段的阻抗幅值靈敏度曲線幾乎與橫軸重合，說明在這些頻段D 變化來使阻抗幅值明顯變化；相角靈敏度在頻率為42、48、52 Hz時較高，說明在這3 個頻率附近的阻抗相角對D 變化比較敏感；而1～40 Hz、54～1 000 Hz 頻段的阻抗相角靈敏度曲線幾乎與橫軸重合，說明在這些頻段D 變化來使阻抗相角明顯變化。上述分析與D 變化時阻抗曲線發生變化的頻段一致。

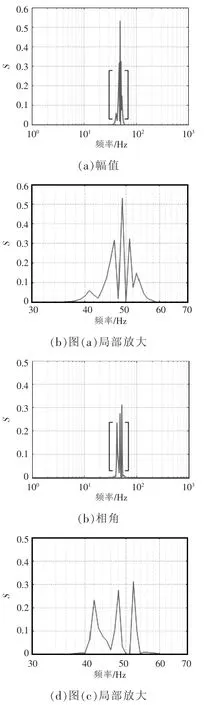
圖8 D 的阻抗靈敏度Fig.8 Impedance sensitivity of D

虛擬轉動慣量J 的阻抗靈敏度如圖9 所示，幅值靈敏度曲線在頻率為43、48、52 Hz 時較高，說明在這3 個頻率附近的阻抗幅值對J 的變化比較敏感；而1～30 Hz、70～1 000 Hz 頻段的阻抗幅值靈敏度曲線幾乎與橫軸重合，說明在這些頻段J 的變化不會使阻抗幅值產生明顯變化；相角靈敏度在頻率為41、47 Hz 時較高，說明在這2 個頻率附近的阻抗相角對J 的變化比較敏感；而1～30 Hz、60～1 000 Hz 頻段的阻抗相角靈敏度曲線幾乎與橫軸重合，說明在這些頻段J 的變化不會使阻抗相角產生明顯變化。上述分析與J 變化時阻抗曲線發生變化的頻段一致。

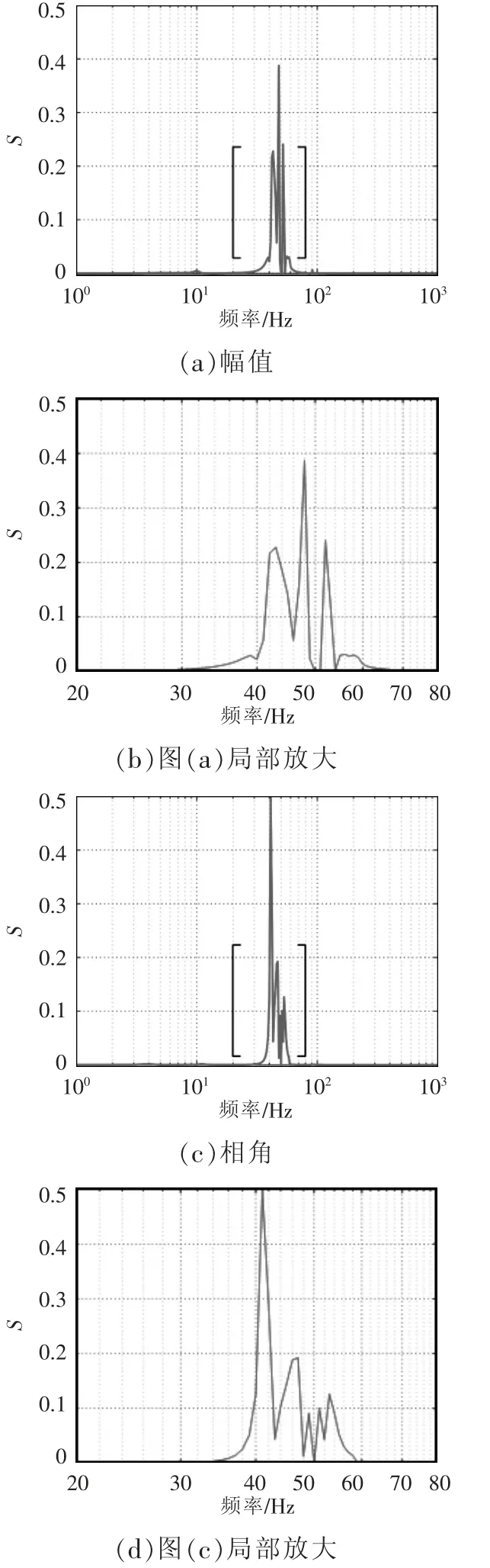
圖9 J 的阻抗靈敏度Fig.9 Impedance sensitivity of J

3.2 穩定性分析

圖10 為MMC 并網系統示意，MMC 和電網參數見表2。輸電線路和變壓器阻抗等效為電網阻抗，包括等效電網電感Lg1、Lg2和等效電網電容Cg。基于VSG 控制策略的MMC 可以視為電壓源，此時MMC 并網系統的簡化拓撲如圖11 所示。

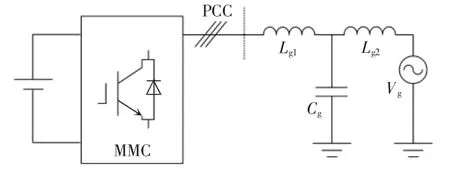
圖10 MMC 并網系統示意Fig.10 Schematic of grid-connected MMC system

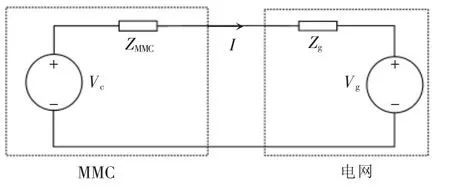
圖11 MMC 并網系統簡化拓撲Fig.11 Simplified topology of grid-connected MMC system

在圖11 中，流過傳輸線路電流I 為

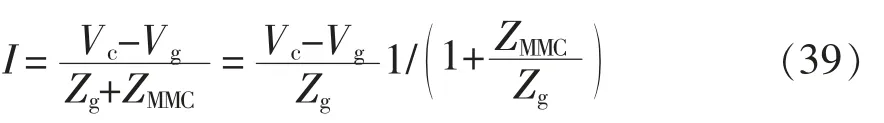
式中：Vc為VSG 策略下MMC 的等效電壓源；Vg為電網電壓；Zg為電網阻抗；ZMMC為MMC 交流端口小信號阻抗。在式（39）中，Vc和Vg是穩態量，而Zg是無源阻抗，因此（Vc-Vg）/Zg也是穩態量。此時系統穩定性取決于1/[1+（ZMMC/Zg）]。根據奈奎斯特穩定判據[10]，當MMC 和電網都是獨立穩定的條件下，通過阻抗比ZMMC/Zg即可判斷系統的穩定性。在MMC 與電網的阻抗交點圖中，若MMC 與電網阻抗幅值交點對應的相角裕度較大，則系統是穩定的，若相角裕度很小，則系統將在該頻率附近振蕩，若相角裕度小于等于0°，則系統將發生振蕩并發散。

圖12 為MMC 阻抗與電網的阻抗伯德圖。二者的幅頻曲線在頻率為32、89、92 和110 Hz 有交點，穩定裕度分別為11.1°、3.0°、165.8°和0.1°，其中，在110 Hz 穩定裕度很小，系統在110 Hz 附近將會振蕩。

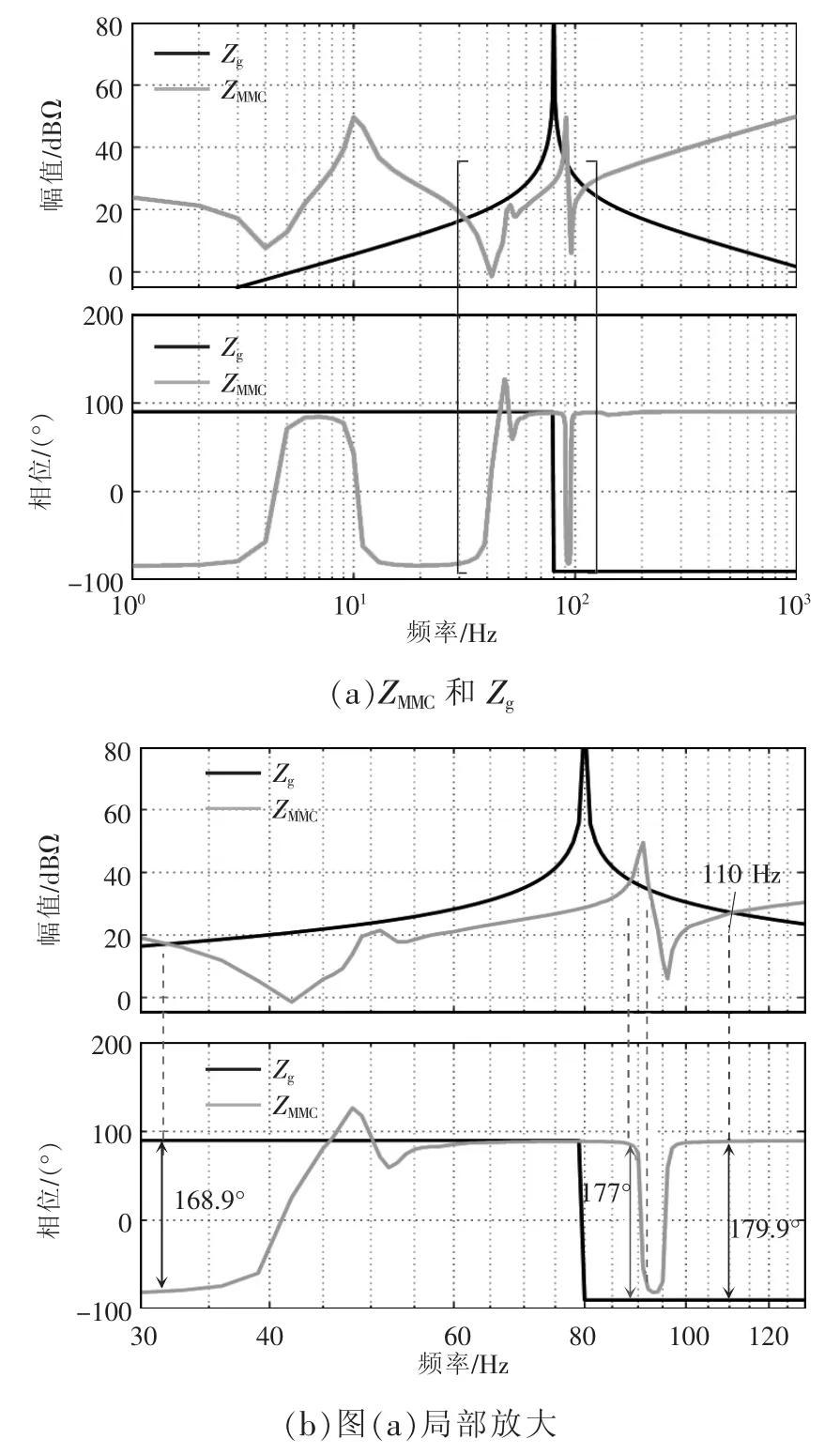
圖12 MMC 并網系統中MMC 阻抗與交流電網阻抗Fig.12 MMC impedance and AC grid impedance in grid-connected MMC system

3.3 實驗驗證

通過硬件在環實驗驗證上述分析。硬件在環實驗系統如圖13 所示，主要由主計算機、目標機、DSP、I/O 卡和示波器等組成。首先在主計算機上用Matalab/Simulink 的工程模式進行編譯，將代碼下載到目標機中進行實時仿真（步長為25 μs）。目標機通過與其連接的多功能I/O 卡（型號Humusoft MF 624）與DSP 進行通信。包含環流抑制控制環節的VSG 控制策略在DSP（型號TMS320F28335）中單獨運行，目標機中的實時模型生成的電壓和電流信號通過嵌入在目標機器中的多功能I/O 卡適當放大并輸出。利用示波器實時監測和記錄目標機提供的電壓和電流波形。PCC 點a 相電流實驗波形如圖14 所示。

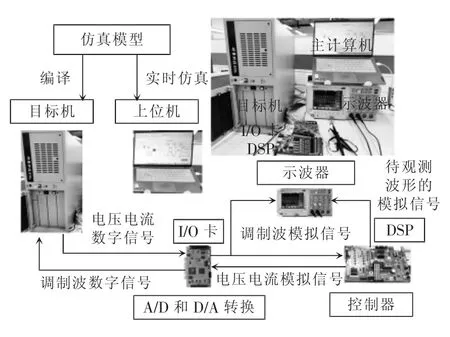
圖13 硬件在環實驗平臺示意Fig.13 Schematic of hardware-in-the-loop experimental platform

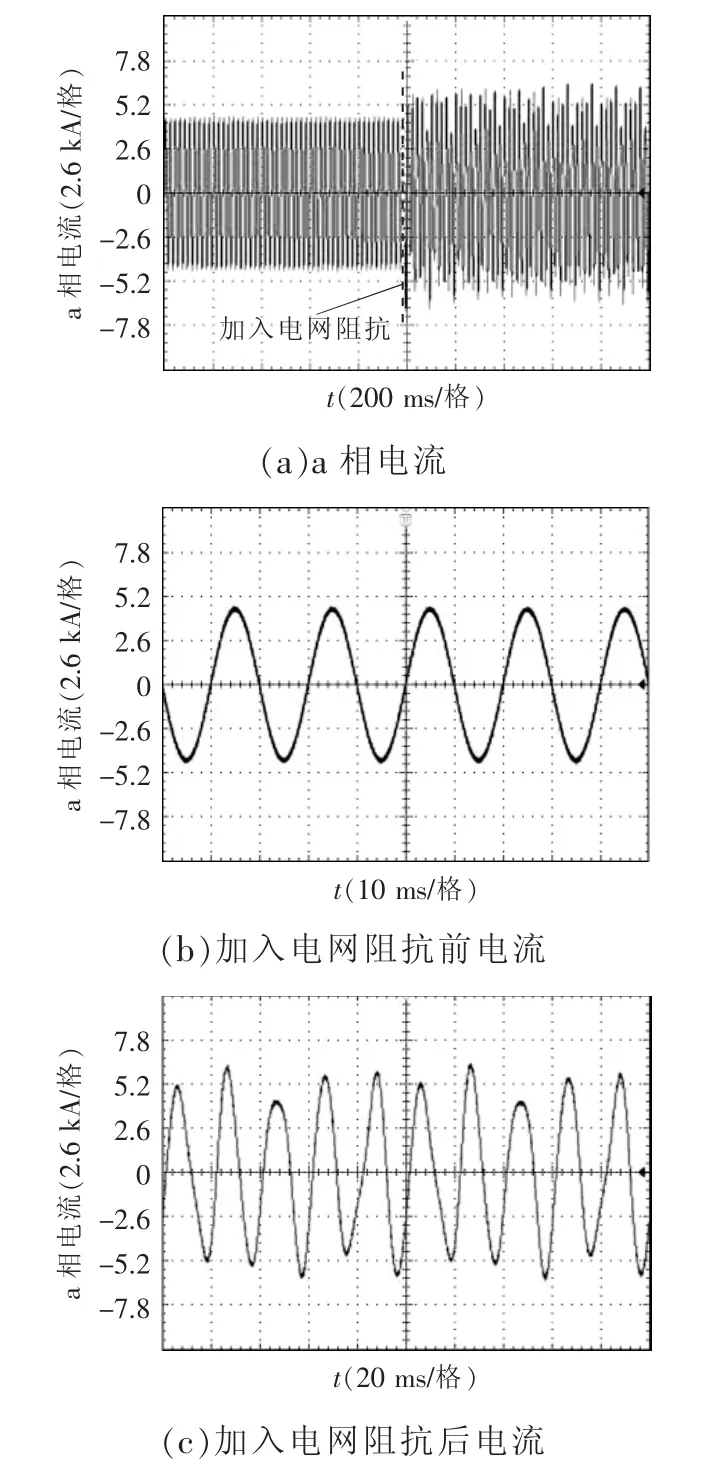
圖14 PCC 點a 相電流實驗波形Fig.14 Experimental waveforms of PCC current in phase a

由圖14 可以看出，加入電網阻抗前，系統運行穩定，當2 s 加入電網阻抗后，PCC 點電流出現振蕩，說明此時系統不穩定，對PCC 點a 相電流進行FFT 分析，結果如圖15 所示。從頻譜圖可以看出，PCC 點a 相電流在110 Hz 處諧波含量大，這與圖12 阻抗交點伯德圖的分析結果一致，說明上述穩定性分析是正確的。

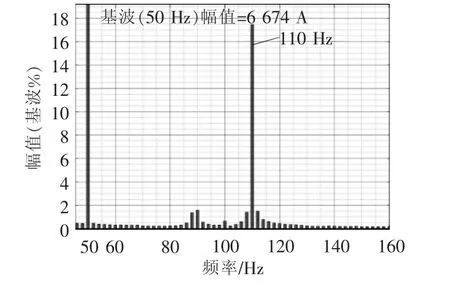
圖15 PCC 點a 相電流諧波頻譜Fig.15 Harmonic spectrum of PCC current in phase a

4 結論

（1）基于VSG 控制策略的MMC 的阻抗特性在低頻段較為復雜，在容性和感性多次變化，高頻段主要呈感性。

（2）VSG 控制參數中的虛擬轉動慣量和阻尼系數對50 Hz 附近的MMC 阻抗有影響，有功-下垂系數較大時對50 Hz 附近的MMC 阻抗有比較明顯的影響。

（3）當電網等效阻抗在高頻段呈容性時，可能會與MMC 阻抗存在諧振點，導致MMC 并網系統在中高頻段出現諧振現象。