筏式海水養殖設施在波浪作用下的水彈性分析

張光明，儲 備，張 堯，張新曙

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240；2. 高新船舶與深海開發裝備協同創新中心，上海 200240；3. 自然資源部海洋減災中心，北京 100194)

近年來，水產品逐漸成為人類獲取優質蛋白質的重要來源。據聯合國糧農組織2020 年報告：世界魚類產量在2018年已經達到1.8億t，其中0.3億t來自海洋水產養殖，而中國貢獻了35%的魚類產量[1]。海水養殖主要分為筏式養殖和深水網箱養殖，筏式養殖設施廣泛分布在我國福建和浙江沿海地區，筏式養殖的產量占海水養殖總產量的33%。

根據相關文獻描述[2]，柬埔寨很早就采用了漁業網箱養殖方式，至今已經經過160多年的發展。挪威的深海養殖技術在世界上處于領先地位，其深水網箱的結構型式多樣，主要包括可移動框構型、環型、張力腿型[3]深水網箱。而美國海上養殖設施中應用更多的是剛性更強的網箱，例如錨拉式或者崇碟型的網箱以及碟型樣式的養殖網箱[4]。大概在20世紀70年代我國才開始使用近海類型網箱養殖，這種類型的構造比較簡易，抵抗風浪的能力比較弱。到20世紀80年代開始進行抗風浪類型的網箱研究，但是成果不多，自從90年代末期引進了挪威產的養殖網箱，我國在該領域的研究才開始進入迅速發展時期[5]。不同于深水網箱，筏式養殖設施主要分布在我國近海，在我國海水養殖業中占據著重要的位置。如圖1所示，在福建省連江縣的木制筏式設施在臺風作用下中遭受嚴重破壞。然而目前對該設施的破壞機理分析較少，其破壞產生的主要原因尚不明確。

圖1 損壞的傳統木制筏式設施(2019年8月拍攝于福建省連江縣)Fig. 1 The damaged traditional wooden raft facilities (The photo is taken in Lianjiang, Fujian Province in August 2019)

對浮筏結構和深海網箱結構的研究有許多相似性，譬如結構都涉及水彈性問題且都有錨繩系統。Fredriksson等[6]開發利用有限元方法來研究高密度聚乙烯(high density polyethylene，簡稱HDPE)材料構成的網箱結構承載能力。吳常文等[7]對深水網箱抗風浪流性能進行驗證試驗，發現風力主要影響扶欄系統,流速主要影響網具系統,而波浪對網箱整體結構均有明顯影響。曾啟東等[8]建立了網衣與其在波浪中的三維數值模型，來研究波浪經過網衣后的變化規律，通過與物理模型試驗結果的對比驗證了該方法的可行性。對于浮筏養殖設施來說，水彈性問題和系泊系統是整個結構系統安全性的重要影響因素。

目前，對筏式養殖設施動力響應的研究并不充分，而涉及該結構水彈性問題的研究則更少。筏式養殖設施與浮橋結構有一定的相似性，對于一座浮橋的研究通常需要包括對水彈性進行有關的分析。對簡化的浮橋結構模型，Viuff等[9]提出了其在非規則波中計算分析的方法。Fu等[10]在三維勢流理論和有限元方法的基礎上，提出了浮橋在非規則波中的水彈性響應數值模型。Viuff等[11]先分別用AQWA和WADAM進行浮筒的水動力系數求解，然后分別施加到SIMO-RIFLEX和OrcaFlex兩個海洋工程應用軟件建立的模型中，來對比研究浮橋的水彈性動力響應，分析了不同商業軟件對浮橋問題研究的誤差和可行性。文中所研究的筏式養殖設施如圖2所示，縱橫交錯的筏式養殖設施相對于長線型的浮橋結構更加復雜。Chu 等[12]對與文中相同的筏式養殖設施在規則波與非規則波下的水彈性響應以及錨泊系統非線性的影響進行了研究。而文中則基于實際應用中的兩種常見筏式養殖設施(木制浮筏與HDPE型浮筏)，研究走板材料(浮筏剛度)對其抗風浪性能的影響。

由于走板材料的不同，浮筏在波浪中的破壞程度也會不同。首先利用勢流面元軟件WAMIT對浮子的水動力系數進行求解，基于海洋工程動力分析軟件OrcaFlex對使用不同走板材料的浮筏結構在波浪中的水彈性響應進行數值模擬和分析，比較了兩類不同走板材料結構上的水動力載荷。

1 數值計算模型

1.1 浮筏結構動力響應方程

筏式養殖設施可以看作一個有一定彈性的梁單元系統，而這個梁單元系統是由多個提供浮力的剛性浮子連接在線單元的走板上組成的。利用OrcaFlex軟件[13]對筏式養殖設施進行建模計算，其計算模型如圖2所示，浮子采用的是6自由度浮體(6D buoy)，可看成一個剛體，且可提供所需浮力。通過在浮子上設置附加質量系數和阻力系數來分別考慮慣性力和黏性力的影響。該浮筏結構不考慮波浪二階力的影響。水深為10 m，錨繩在4個方向分別布置2根，總共8根，每個方向的2根錨繩一端連接最靠近結構角點處的浮子，另一端固定在海底，錨繩連接點的水平距離為50 m，錨繩總長為52 m。

圖2 筏式養殖設施模型示意Fig. 2 Sketch of the whole structure modelled in OrcaFlex

理論上求解筏式養殖設施結構的時歷運動響應需要利用卡明斯方程，如式(1)所示：

(1)

由于浮子尺寸很小，而且根據Chu等[12]的結果，浮子的附加質量系數在所關心的波浪周期內變化不大，波浪阻尼系數相對于附加質量系數很小。因此，忽略式(1)中的延遲函數項，采用Morison公式求解浮子在波浪中水動力。

(2)

其中，ρ表示流體密度；Ad表示浮子截面積；U，af分別表示浮子中心處流體速度與加速度；CD表示浮子在波浪中的拖曳力系數。從而，整個浮筏結構運動方程可以簡化為:

(3)

1.2 附加質量計算

浮子的附加質量系數通過勢流軟件WAMIT[14]求解得到。WAMIT是MIT的Newman教授團隊開發的軟件，它通過基于頻域的面元模型來求解浮體的輻射繞射問題。圖3(a)表示單個浮子模型和主尺度，浮子長度為0.9 m，直徑為0.65 m，設計吃水d為0.2 m，oxyz為浮子局部坐標系，x方向為軸向，y方向為法向，z方向垂直向上；圖3(b)表示單個浮子在WAMIT中的面元模型；圖3(c)中定義了波浪的入射方向，全局坐標系OXYZ，浪向角β，該坐標系與圖2(b)中的坐標系重合。

圖3 浮子的主尺度、面元模型及坐標系Fig. 3 The principal dimensions, panel model of the buoy and the incident wave directions

單個浮子可以看成浮于海面的水平圓柱，在WAMIT中采用高階面元法來求解浮子的水動力系數。基于勢流理論，速度勢Φ需滿足拉普拉斯方程：

?2Φ=0

(4)

總的速度勢Φ可以寫為：

Φ=Re(φeiωt)ω

(5)

其中，φ為空間速度勢，Re表示取實部，ω是物體運動頻率，t表示時間。空間速度勢的自由面條件為：

φz-Kφ=0，z=0

(6)

其中，K=ω2/g表示無限水深波數。入射波速度勢定義為：

(7)

其中，k表示有限水深入射波的波數，為ω2/g=ktanhkH的實根，A表示入射波的波幅，H為水深。

將空間速度勢φ分解成輻射勢φR和繞射勢φD兩部分：

φ=φR+φD

(8)

(9)

φD=φ0+φs

(10)

其中，ξj是浮體6自由度運動的幅值，φj表示相應的輻射勢，j=1,2，……，6。速度勢φs表示當浮體固定時由入射波引起的散射速度勢，而入射波速度勢和散射波速度勢合成了繞射勢φD。輻射勢需在無窮遠處滿足輻射條件。輻射勢和繞射勢的物面分別如下：

φjn=nj

(11)

φDn=0

(12)

其中，向量n為物面的法向量，n=(n1,n2,n3)，x=(x,y,z)，x×n=(n4,n5,n6)。

浮體附加質量和波浪阻尼系數可通過式(13)計算：

(13)

其中，Sb表示平均濕表面。附加質量和波浪阻尼系數的無量綱形式為：

(14)

其中，p=3對應i,j=1,2,3;p=4對應i(j)=1,2,3,j(i)=4,5,6;p=5對應i,j=4,5,6。

在對浮子水動力系數進行網格收斂性分析時，設置了3組不同尺度的面元模型，面元尺寸分別為0.20 m，0.10 m和0.05 m。圖4表示浮子無因次橫蕩附加質量隨周期的變化，如圖所示網格大小為0.10 m時結果已收斂，后續采用0.10 m的網格計算附加質量。

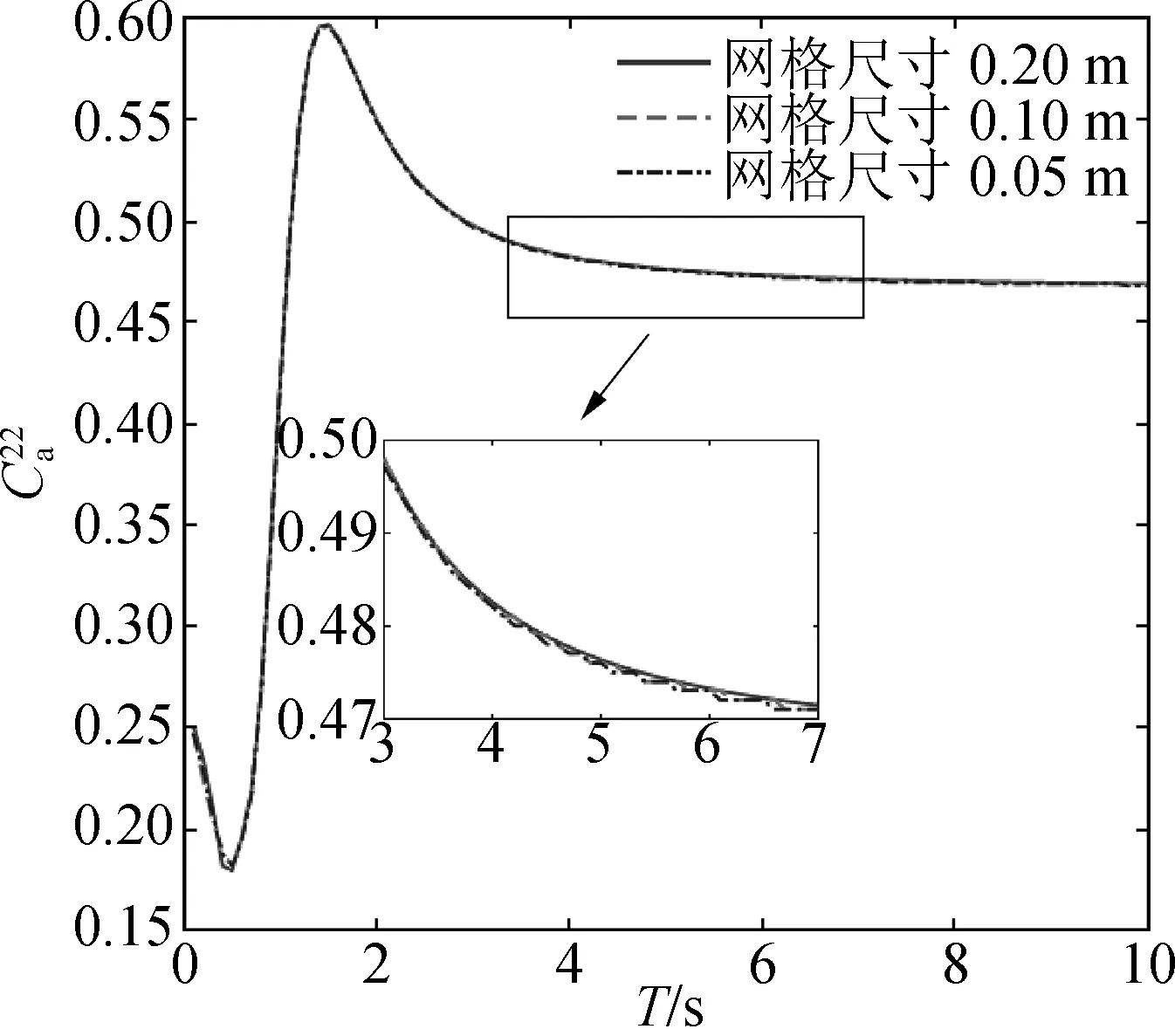
圖4 浮子橫向附加質量系數隨周期的變化Fig. 4 The added mass of the buoy in sway with respect to wave periods

1.3 阻力系數計算

浮子所受的黏性力對其動力響應有較大影響。計算浮子在波浪中的阻力系數時需要注意以下兩點：流體運動的周期性和自由面的影響。由于自由面的影響，浮子的阻力系數可能與Sarpkaya等[15]的浸沒圓柱在振蕩流中的阻力系數不同。依據挪威船級社規范DNV-RP-C205[16]里建議的方法，當浮子的運動幅值比結構的特征尺度大時，結構在靜水中的搖蕩阻尼系數可以用作結構在波浪中的阻力系數。因此，浮筏設施的浮子阻力系數可以通過浮子在縱蕩方向的阻尼系數來估算。令浮子在縱蕩方向進行強迫振動x(t)=X0cos(2πt/T)，X0表示振蕩運動的幅值，T是振蕩的周期。使用商業軟件STAR-CCM+[17]計算浮子的阻力系數。選擇求解雷諾平均N-S方程(RANS)并采用k-ω SST湍流模型，用流體體積方法(volume of fluid，簡稱VOF)來捕捉自由液面。

對浮子在橫蕩方向和縱蕩方向的受力時歷曲線進行傅里葉變換可以得到其所在對應方向的阻力系數。利用莫里森方程擬合得到浮子的阻力系數，作用在浮子上的縱向力可以表示為：

(15)

式中：V是浮子的體積，Ax是浮子在x方向的濕表面投影面積。在計算模擬中經過3個振動周期后，浮子的附加質量系數Ca和阻力系數CD趨于平穩。當各系數達到穩定后，對其取平均值，得到浮子在軸向和徑向的阻力系數分別為0.58和0.23。這兩個系數是后續在OrcaFlex中計算的設置系數。

2 結果分析

2.1 浮筏計算參數設置

浮筏設施各組成部分的類型和參數如表1所示，為了對比不同材料剛度對浮筏結構響應的影響，對連接走板設置了3種不同的材料剛度，HDPE材料和木材走板(WOOD)，以及設置了一半木板剛度的走板(HWOOD)，其剛度參數見表2。走板的截面形狀如圖5所示。表1中走板的直徑為軟件OrcaFlex中視圖的直徑，計算載荷是利用截面形狀的參數來后處理的。連接浮子可以傳遞相交走板的載荷，其體積和質量可以忽略。每兩個浮子間的連接走板長度多數為0.78 m，只有浮筏內部Y方向為1.08 m。

表1 浮筏設施組成部分的建模類型和參數Tab. 1 The parameters of components of the floating raft

表2 不同走板的材料及其對應參數Tab. 2 The parameters of different plates

比較不同走板材料對浮筏結構動力響應的影響。設置了不同的非規則波條件如表3所示。非規則波采用Jonswap波浪譜，其中參數參見Isherwood等[18]研究中的取值，波浪過零周期Tz從5～9 s每間隔0.5 s取值，有效波高2 m，浪向角0°。每組計算模擬筏式養殖設施在非規則波中1 h的結構動力響應時歷。

圖5 走板橫截面模型示意Fig. 5 The sketch of the cross section of the plate

表3 非規則波參數Tab. 3 The parameters of the irregular waves

2.2 不同走板剛度的浮筏結構動力響應

錨繩所受到的張力過大導致的錨繩斷裂和走板上受力超過其承受極限而導致的破壞是浮筏結構在波浪中損壞失效的兩種主要形式。計算不僅需要考慮錨繩所受到的張力影響，也要考慮連接走板上所受的力和力矩的影響。由軟件可以計算得到拉力，剪力，彎矩和扭矩等值，然后根據經驗公式[19]來估算走板截面上的正應力和剪應力：

(16)

式中：σpl和τpl分別為走板橫截面上的正應力和剪應力；FTpl，FSpl，Mpl和TSpl分別為其橫截面上的拉力，剪力，彎矩和扭矩；h0為走板高度，b0為寬度，d0為其壁厚，如圖5中所示；Ap和Iyy分別表示其橫截面積和橫截面在y軸方向的慣性矩。走板橫截面正應力是由其橫截面上所受到的拉力和彎矩合成的最大應力，剪應力是由其所受到的剪力和扭矩合成的最大應力。

圖6表示不同材料剛度的浮筏結構其錨繩和走板上載荷的均方差(STD)隨波浪過零周期的變化，均方差能夠反映結構上的載荷在時歷曲線中的總體變化情況。從圖6中可以很直觀地看到兩種不同材料對浮筏結構響應所帶來的影響，HDPE走板材料下的錨繩張力和走板上的拉力、剪力、彎矩以及扭矩的均方差明顯小于另外兩種木材走板的計算結果。隨著波浪周期的增大，各走板材料下錨繩的張力、走板截面上的剪力和扭矩先增大隨后減小，這些載荷的均方差在波浪周期6 s左右達到最大值。而走板截面上拉力和彎矩隨著波浪周期的增大逐漸變小，在短波條件下(Tz=5 s)拉力和彎矩有最大值。如圖6(d)所示，從載荷均方差的相對大小可以看出，材料剛度對結構響應中走板截面上的彎矩影響最顯著。而從材料的特性可知，木板的剛度最大，而木板制成的浮筏在實際海況中最容易破壞，這說明在實際海況中，所用的材料對走板截面上的彎矩承受能力有很大的影響，從而很可能對結構的安全性能產生很大的影響。

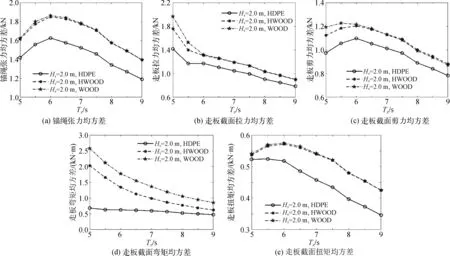
圖6 錨繩和走板上載荷的均方差隨波浪周期的變化Fig. 6 The STD of the loads of the structure in irregular waves with respect to Tz

根據式(16)可得到走板截面的正應力與剪應力。圖7中展示了不同非規則波下走板截面的正應力和剪應力的均方差。圖7(a)和(b)中，木質走板下的應力明顯比HDPE材料走板下的應力要大。圖7(a)中所示同一波浪條件下，走板剛度越大其截面所受正應力的均方差越大。另外，走板截面所受的正應力明顯大于其所受剪應力。所以走板材料剛度越小時，走板上所受到的彎矩越小，則其正應力也越小，結構越不容易破壞。由于HDPE材料具有很好的柔性而木板很硬幾乎是剛體，所以當浮筏受到波浪載荷時，柔性材料可以很好緩解結構受力不均所帶來的彎矩過大問題，而木板則產生很大的彎矩，結果表明木制結構浮筏可能更容易遭受破壞。

圖7 走板截面的應力均方差隨波浪周期的變化Fig. 7 The STD of the stress of the plates in irregular waves with respect to Tz

圖8展示了非規則波下浮筏結構中心處的水平位移和垂直位移均方差隨波浪周期的變化。從圖8中可以看出，走板材料的不同，結構的位移也會有差異，木制走板材料的水平位移比HDPE大，前者垂向位移比后者小。隨著波浪周期的增大，結構中心的水平位移先增大后減小，在波浪周期6.5 s左右，水平位移均方差有最大值，垂向位移幾乎隨著波浪周期的增大而增大。結構的水平位移總體要比垂向位移大許多，幾乎是2倍關系。結構在波浪中的水平位移越大導致錨繩所受的張力也越大，浮筏結構走板截面上的各受力和力矩以及應力也越大，結構越容易破壞。HDPE材料制成的走板浮筏結構不僅在水平位移上要比木板小得多，其錨繩所受的張力、木板上所受的力和力矩以及應力也更小。在同等的破壞強度下，綜合來看采用剛度更小、更具有柔性的HDPE材料作為浮筏走板材料更加安全可靠。從以往臺風影響下近海浮筏漁排受損情況來看，HDPE材料制成的浮筏比傳統木板制成的浮筏漁排更能抵抗風浪，這也和文中的結果一致。

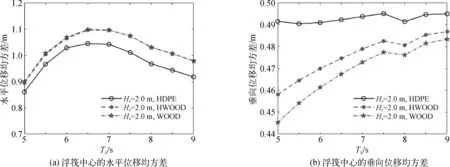
圖8 浮筏中心的位移均方差隨波浪周期的變化Fig. 8 The STD of the motion of the structure in irregular waves with respect to Tz

2.3 浮筏動力響應的極值估計

根據Faltinsen[20]的研究，海洋平臺等結構物在隨機海況中的響應極值可以通過經驗估算得到大概值，前提是這個值的數學統計結果有足夠長的時歷曲線結果，且這個統計結果要滿足瑞利分布，最可能出現的最大值估計(MPM)可以通過式(17)估算：

(17)

式中：σm(X)表示變量X的均方差，td表示監測的持續時間，Tz表示波浪的過零周期。

由前面的分析可知，浮筏結構在波浪周期為6 s時所受載荷比較大，因此對波高為2 m，波浪周期為6 s，浪向角為0°的浮筏位移進行最大值估計分析。為了方便表示，文中定義M1=|MAX′-MEAN|，M2為式(17)所求，Errorm=(M2-M1)/M1。其中MEAN表示時歷曲線的平均值，MAX′表示離平均值最遠的值，M1表示時歷曲線中離平均值最遠距離的絕對值，M2表示變量的最大值估計MPM，Errorm表示最大值估計M2與M1誤差百分比。

圖9為浮筏中心處位移的時歷曲線，不同材料剛度的走板位移時歷曲線沒有表現出很大的差異。圖10表示浮筏中心位移的功率譜，水平位移功率譜的最大值約為垂向的5倍，說明水平方向的能量更大，而木板WOOD材料的功率譜值比HDPE材料的值更大，反映出在同樣海況下木板結構的水平位移會比HDPE的大。圖11是浮筏中心處位移的直方圖分布情況，直方圖中使用木板情況下浮筏中心位移絕對值大于2 m的N(X)數量比使用HDPE情況下的更多，這些結果反映了和功率譜一致的規律，即木板材料剛度下結構出現較大水平位移的可能性更大。根據公式(17)的最大值估計與時歷曲線的最大值進行統計分析得到表4中的結果。表4中結果表明HDPE材料下的時歷曲線中位移最大值小于木板的情況。垂向位移的最大值估計MPM結果與實際最大值的誤差約為1%，水平位移的最大值估計結果誤差在16%左右，這是由錨繩系統的非線性特性導致的。

圖9 非規則波下浮筏中心的位移時歷曲線(Tz=6 s)Fig. 9 The time history curves of the structural motion (Tz=6 s)

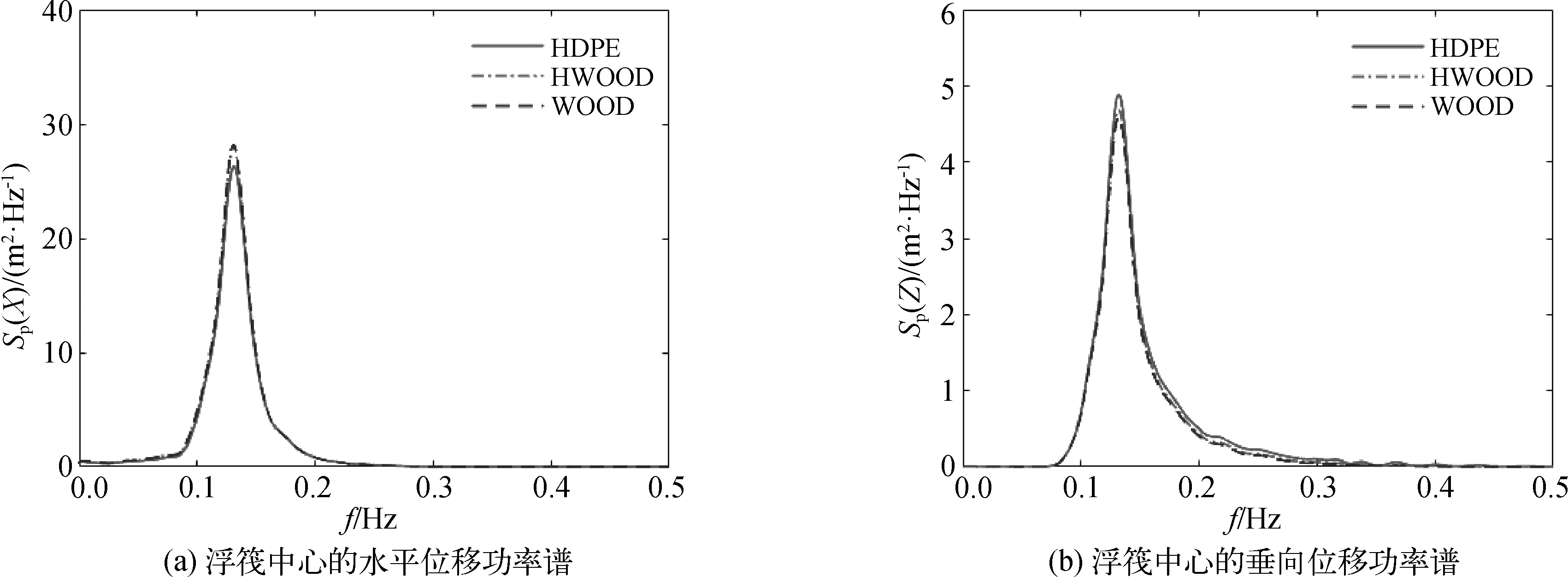
圖10 非規則波下浮筏中心的位移功率譜(Tz=6 s)Fig. 10 The power spectrum of the structural motion (Tz=6 s)

圖11 非規則波下浮筏中心的位移分布直方圖(Tz=6 s)Fig. 11 The histogram of the structural motion(Tz=6 s)

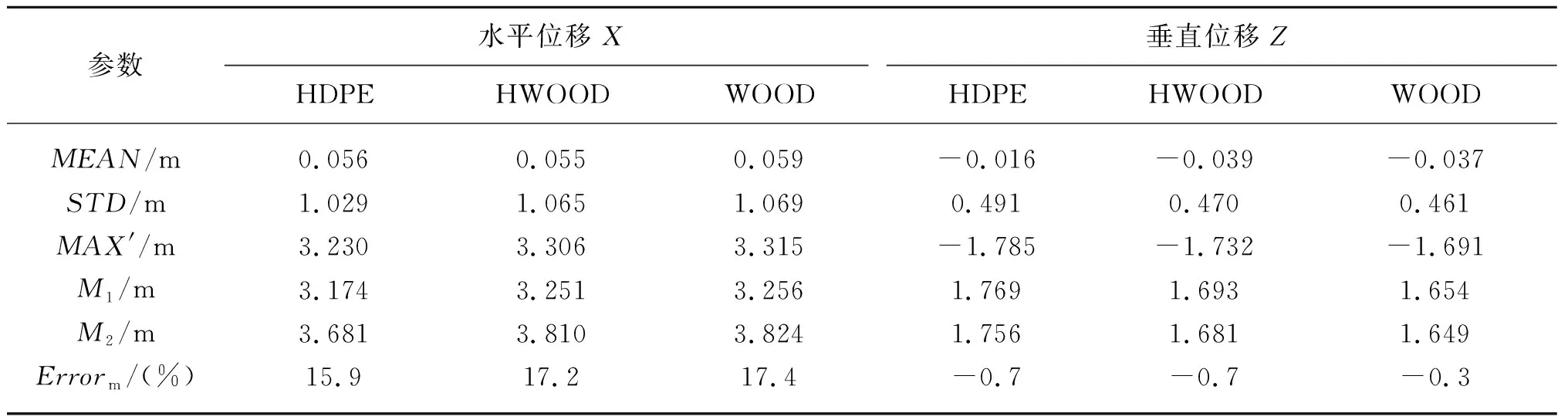
表4 非規則波中不同走板材料的結構位移統計分析Tab. 4 The structural motion in the irregular waves with different plate materials

3 結 語

對非規則波下采用不同走板材料浮筏設施的水彈性響應進行了計算和比較。利用WAMIT計算了浮子的附加質量系數，利用CFD軟件計算了浮子的阻力系數，然后使用OrcaFlex對采用HDPE和木板兩種不同走板材料的3種不同剛度浮筏結構進行了動力響應計算，得出如下結論：

1) 隨著波浪周期的增大，不同材料剛度下錨繩的張力、走板截面上的剪力和扭矩先增大隨后減小，波浪周期Tz在6 s左右這些載荷的均方差達到最大值。而走板截面上拉力和彎矩隨著波浪周期的增大逐漸變小，在短波條件下拉力和彎矩有最大值；材料剛度對走板截面上的彎矩影響最大。

2) 同一波浪條件下，走板剛度越大其截面所受正應力的均方差越大，且正應力明顯大于剪應力，走板材料剛度越小時走板上受到的彎矩越小，則其正應力也越小，這表明當浮筏在波浪中運動時，柔性材料可以很好緩解結構受力不均所帶來的彎矩過大問題。

3) 相同波浪條件下，當走板采用木板材料時浮筏結構的水平運動最大幅值比使用HDPE材料的大，結構在波浪中的水平運動最大幅值越大則錨繩所受的張力也越大，結構走板截面上的各受力和力矩以及應力也越大，結構也越容易破壞。

4) 垂向位移的最大值估計MPM結果與直接模擬最大值的誤差約為1%，水平位移的最大值估計結果誤差約為16%。綜合來看，在同等的材料破壞強度下，采用剛度更小、更具有柔性的HDPE作為浮筏的走板材料可能更加安全可靠。