砂土地基中箱筒型防波堤基礎穩定性試驗研究與機理分析
周 超,寇海磊, 2,閆正余,刁聞宙,周 楠,陳 琦
(1. 中國海洋大學 工程學院,山東 青島 266100; 2. 青島理工大學 藍色經濟區工程建設與安全協同創新中心,山東 青島 266033)
隨著經濟與港口建設的發展,我國近海防波堤結構基礎需要面對的地質條件及風、浪、流等荷載條件更加復雜,傳統重力式防波堤基礎已經不能滿足近海海洋結構物的正常使用,基礎失穩的狀況時有發生[1-2]。近些年來吸力式箱筒型防波堤基礎,具有安全可靠性高、能耗少、安裝作業方便等優勢,應用越來越廣泛[3]。
作為一種新型基礎結構,吸力式箱筒型防波堤受力機理更為復雜。喻志發等[4]依據現場工程實測數據,通過預埋鋼筋計和實時測試對箱筒型防波堤基礎筒、連接墻、蓋板等進行受力分析,為設計優化提供了依據;Guan等[5]依據筒型防波堤基礎的現場監測數據,揭示了基礎周圍土體應力、孔隙水壓力隨時間周期性變化的規律;Yan等[6]通過室內模型試驗對筒型防波堤基礎豎向承載力及筒砂相互作用機理進行了研究,指出基礎失穩以整體剪切破壞為主;彭增亮[7]針對箱筒型防波堤基礎建立了氣浮穩定計算分析方法,表明箱筒型防波堤基礎氣浮托運在技術上是可行的;吳鳳亮等[8]通過PLAXIS有限元軟件對箱筒型防波堤基礎用線彈性模擬,地基土用摩爾—庫倫和蠕變模型模擬,并考慮結構和地基土之間的界面接觸對其沉降變形進行分析,表明采用箱筒型防波堤基礎能夠有效減少預留沉降量;李元音等[9]采用有限元分析法、數值極限平衡分析法和簡化極限平衡分析法對箱筒型防波堤基礎斷面穩定性進行計算,表明即使不打設迎浪側和背浪側的砂樁斷面也是穩定的,為結構優化提供了基礎;李武等[10]利用物理模型試驗和數值模擬相結合的方式,探討了基礎埋深、土體摩擦角、彈性模量、黏聚力等因素對桶式防波堤基礎穩定性的影響,指出增大摩擦角、黏聚力、基礎埋深對承載力的提高有顯著作用;蔣敏敏等[11]利用離心模型試驗得到箱筒型防波堤基礎在水平靜荷載作用下處于極限狀態時的位移和土體中超靜孔壓響應,表明荷載達到約3倍設計值時達到極限狀態,防波堤發生向港側水平位移及傾斜,并且荷載作用下港側基礎周圍孔壓增大,海側周圍孔壓降低,而且港側筒內超靜孔壓始終大于筒外超靜孔壓;王元戰等[12]利用數值模擬對不同波浪荷載作用下箱筒型防波堤基礎上土壓力大小以及環向分布進行分析并建立了不同土壓力之間的簡便計算方法,為箱筒型防波堤基礎穩定性驗算提供了基本依據;茅加峰等[13]利用離心模型試驗對箱筒型防波堤進行擬靜力水平加載,認為在水平荷載大于某一臨界值后,荷載位移曲線出現類似屈服的現象,背浪側和迎浪側地基中分別出現正和負超靜孔壓,而箱筒型防波堤的主要破壞模式是過度傾斜而失穩;李斌等[14]和肖忠等[15]基于極限平衡法分析了不同結構尺寸對箱筒型防波堤基礎穩定性的影響,表明筒高變化對抗滑移穩定性影響最大,傾覆極限狀態時轉動點位置無量綱化l/L在0.5附近;舒曉武等[16]對箱筒型防波堤基礎結構進行受力分析及抗滑移、抗傾覆、地基承載力穩定性計算,得到結構尺寸與穩定性的關系,合理優化結構尺度。上述研究雖然對箱筒型防波堤基礎的受力機理及穩定性進行了研究,但對其荷載作用下轉動點變化及其對穩定性的影響研究相對較少。
通過室內模型試驗及理論分析,對水平靜荷載、循環荷載作用下的箱筒型防波堤基礎轉動中心變化進行了研究。在此基礎上,根據極限平衡理論對箱筒型防波堤基礎抗滑移、抗傾覆等穩定特性進行分析,為箱筒型防波堤基礎的理論研究提供依據。
1 試驗設置
1.1 試驗裝置
室內模型試驗在一個由數據采集系統、模型箱以及荷載施加系統3部分組成的試驗裝置上進行,如圖1所示。模型箱使用一個圓柱形不銹鋼罐槽,直徑800 mm,高1 000 mm。室內模型試驗所采用的是福建標準砂,粒徑為0.25 mm。試驗砂床的制備方法是采用砂雨法將干砂以250 mm的落距均勻的撒在模型箱內,其中每灑落50 mm左右的砂層進行一次平整,如此反復將砂床高度鋪到800 mm左右進行靜置7 d,最終砂床的高度為800 mm。靜置完成之后取模型箱內砂樣進行土工試驗,確定砂床的最大干密度ρdmax、最小干密度ρdmin、內摩擦角θ、相對密度Dr等參數,具體參數見表1。試驗過程中,箱筒型防波堤基礎通過連接桿與作動機器相連進行豎向貫入、水平靜載荷和循環加載試驗。作動機器包括伺服電機、控制器、齒輪變速箱和測壓元件。模型基礎的力和位移均通過安裝在加載桿底部的壓力傳感器和位移傳感器測得,其中壓力傳感器的量程為50 kN,精度為0.01 kN,位移傳感器的量程為1.0 m,精度為0.001 m。伺服電機速度范圍為0.0~40.0 mm/min。

表1 砂樣相關物理參數Tab. 1 Related physical parameters of sand samples
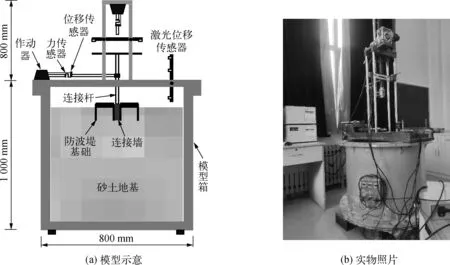
圖1 模型裝置Fig. 1 Model installation diagram
1.2 基礎模型
試驗中采用的箱筒型防波堤基礎模型由4個相同的不銹鋼圓筒、4個連接鋼板以及1個上部蓋板組成,如圖2所示。單個不銹鋼圓筒高H0為90 mm,外徑D0為120 mm,壁厚T0為2 mm,上部蓋板厚度T1為5 mm,連接墻厚度T2為5 mm。不銹鋼圓筒之間通過連接板相連,圓筒與連接板之間通過螺絲固定,上部蓋板與連接板之間也通過螺絲固定。為方便模型試驗加載,在不銹鋼圓筒頂部通過螺絲固定頂帽,用一個5 mm厚的十字鋼板通過螺栓把加載桿與模型基礎連接起來。
1.3 試驗方案
模型試驗按照天津港防波堤工程中箱筒型防波堤基礎方案設計,模型比尺為1∶100,波浪周期為8.1 s。試驗采用40.0 mm/min的恒定速度貫入砂土地基,最終貫入深度約為68.29 mm,貫入力為1.51 kN。為避免砂土擾動對試驗結果的影響,每次試驗結束后均對砂床采用砂雨法重新制備。貫入結束靜置24 h后進行水平靜載荷試驗,依據文獻[17]試驗采用分級加載方式進行,試驗共分10級進行加載,每級加載力大小為0.14 kN,加載速度為6 mm/min,水平位移無明顯變化時即可進行下一級加載。水平靜載荷試驗過程中,所施加水平力與水平位移分別由力傳感器及LVDT位移傳感器測得。
根據文獻[18]確定水平循環加載過程中所施加循環力大小。采用荷載循環比ζc、ζb來描述循環荷載特性:
ζc=Hmin/Hmax
(1)
ζb=Hmax/Hus
(2)
式中:Hmin為循環過程中施加荷載的最小值;Hmax為循環過程中施加荷載的最大值;Hus為水平靜載荷試驗確定的水平極限承載力;ζc的值介于-1(雙向循環)到1(靜力加載)之間;ζb表示循環施加荷載大小。試驗中,選取ζb=0.5以及ζb=1.0進行雙向循環加載試驗以模擬正常工況、極端工況。試驗循環次數為50次,加載速度為6 mm/min,循環加載示意如圖3所示。循環加載過程中利用激光位移傳感器對加載過程中的轉角進行監測(圖1(a))。采用激光位移傳感器量程為1 000 mm,精度為0.000 1 mm。

圖3 循環加載示意Fig. 3 Schematic diagram of cycle loading
2 結果與討論
2.1 水平承載特性
試驗水平靜載荷曲線如圖4所示,據此可判定箱筒型防波堤基礎在水平荷載作用下的極限承載力。文獻[19]建議的4種筒型防波堤基礎的失穩破壞準則為:1) 極限承載力判別標準;2) 基于荷載位移曲線出現較明顯拐點作為穩定判別標準;3) 基于允許變位的判別標準;4) 將筒底脫離臨界點作為穩定性判別標準。文中采用基于荷載位移曲線出現較明顯拐點作為穩定判別標準來確定箱筒型防波堤基礎的水平極限承載力,如圖4所示,在水平力達到0.08 kN 時出現明顯拐點,可以確定在模型試驗中箱筒型防波堤基礎的水平極限承載力為0.08 kN。為方便敘述,定義箱筒型防波堤基礎水平極限承載力Pmax=0.08 kN。
文獻[20-21]認為吸力式基礎在水平靜荷載作用下的承載性狀可以由荷載位移曲線來反映,并且將其分為準彈性階段、塑性階段、破壞階段。如圖4所示,水平靜載荷曲線分成3個階段:準彈性階段內,基礎位移很小,最大水平位移約占筒徑的0.5%左右,基礎位移形式以水平滑動為主,基礎破壞形式以滑移破壞為主,此時主要考慮基礎是否滿足抗滑移穩定性的要求;塑性階段內,基礎位移逐漸增大,最大水平位移約占筒徑的5%左右,基礎位移形式是水平滑動和轉動的組合,基礎破壞形式要綜合考慮滑移破壞和傾覆破壞;破壞階段內,基礎水平位移迅速增加,具體表現為在力變化不大的情況下,水平位移急速增加,此階段內,基礎位移形式以轉動為主,基礎破壞形式以傾覆破壞為主。
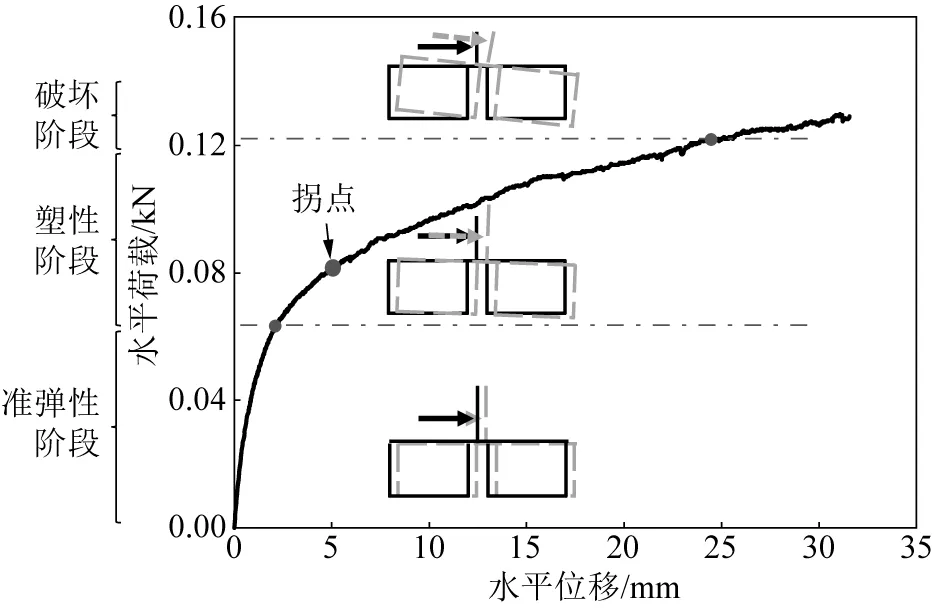
圖4 水平靜載荷曲線Fig. 4 Horizontal static load curve
2.2 循環承載特性
水平循環荷載過程中,最初的10次循環對樁基動力響應具有重要影響[22]。試驗循環位移無量綱化與循環次數的曲線如圖5所示,在0.04 kN(ζb=0.5)循環荷載作用下,前10次累積位移ymax/D為0.005 9,占循環累計位移的96.70%,而后40次循環累計位移ymax/D僅為0.000 2,占循環累計位移的3.30%;0.08 kN(ζb=1.0)循環荷載作用下,前10次累積位移ymax/D為0.087 1,占循環累計位移的91.88%,而后40次循環累計位移ymax/D僅為0.007 7,占循環累計位移的8.12%。造成這種現象的主要原因是剛開始砂土之間內摩擦不能馬上抵抗外力干擾,砂土顆粒間進行重新分布,砂土發生剪脹,以剪切變形為主從而導致前10次循環的累計變形位移較大;10次循環過后,砂土顆粒之間的重新排列已基本完成,在循環荷載作用下,砂土逐漸緊密,砂土發生剪縮,累計循環位移變小。
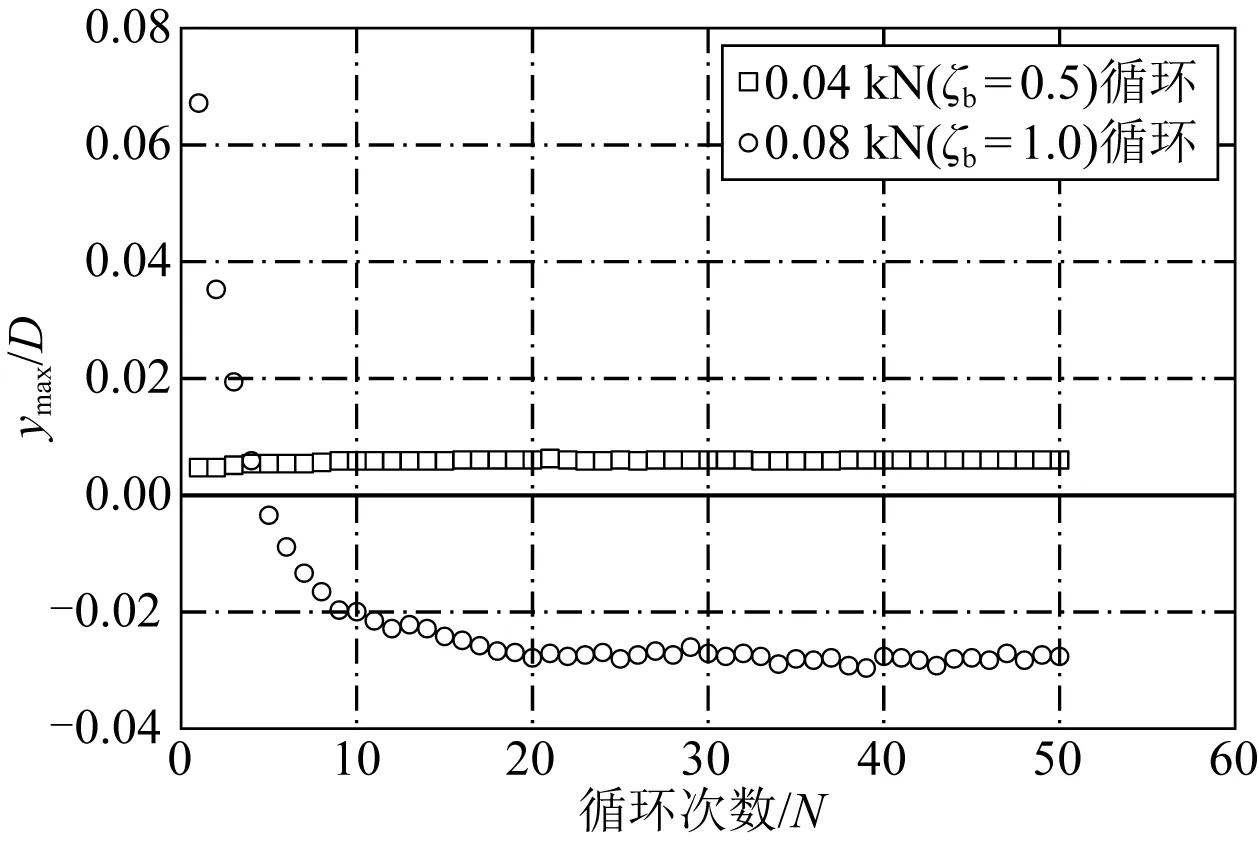
圖5 位移無量綱化與循環次數曲線Fig. 5 Dimensionless displacement and cycle number curve
2.3 轉動特性分析
根據激光位移傳感器數據,可計算防波堤基礎轉角及轉動中心位置,計算簡圖如圖6所示。
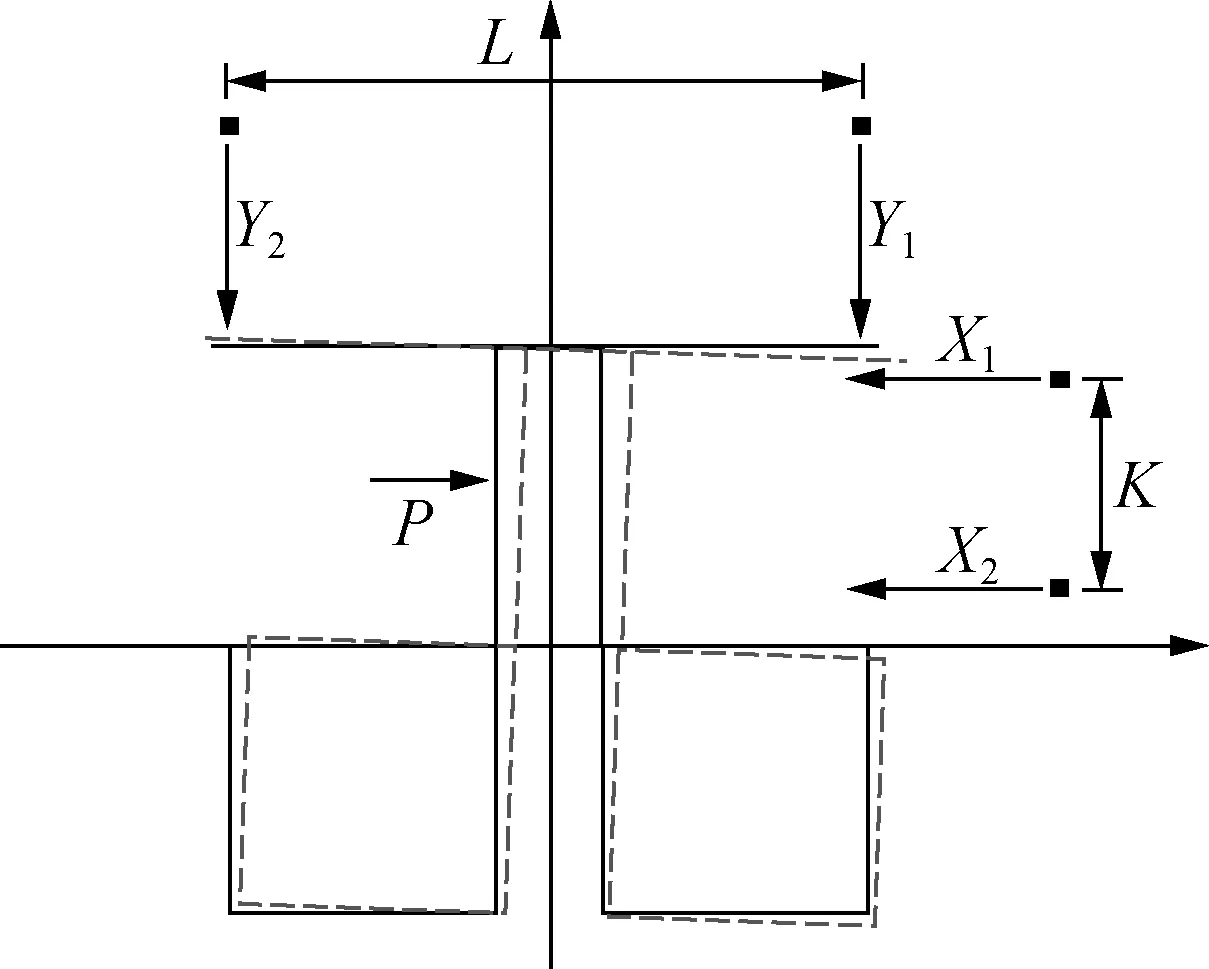
圖6 轉動角度計算簡圖Fig. 6 Simplified diagram of rotation angle calculation
轉動角度為:
ψ=arctan[(X1-X2)/K]
(3)
轉動中心為:
y=X1/tanψ-X0
(4)
x=L/2-Y1L/(Y1+Y2)
(5)
其中,X1、X2、Y1、Y2為激光位移傳感器讀數差值,為正值;X0為激光1到筒底的距離;H0為筒高;K為豎向激光1、2之間的距離;L為箱筒型防波堤基礎的整體長度;x為轉動中心距離筒中心的距離;y為距離筒底面的距離,底面以上取正值。
根據式(3)~(5),可得出水平靜載荷作用下防波堤基礎處于極限狀態時的轉角ψ=0.61°,轉動中心O的位置為x=44.55 mm,y=57.52 mm,即處于極限狀態時轉動中心位于筒底以下。正常使用狀態下,即水平力PN=0.04 kN 時,ψ=0.11°,轉動中心O的位置為x=64.80 mm,y=8.70 mm,轉動中心同樣位于筒底以下,這與文獻[19, 23]描述一致。與沉入式圓筒防波堤不同,箱筒型防波堤基礎并不是繞著泥面以下、筒底以上某點轉動,而是繞著基礎筒底以下的某點發生轉動,主要是因為箱筒型防波堤基礎是一種寬淺式的薄壁筒型結構物,其水平尺寸一般大于其入土深度。
根據式(3)~(5),可得出50次循環過程中每個循環位移最大值時,箱筒型防波堤基礎轉動中心的位置,如圖7所示。在0.04 kN(ζb=0.5)循環荷載作用下,轉動中心的位置向右斜下方發展,但是變化幅度不是很大。由圖4可知,砂土基本處于彈性階段,砂土顆粒的重分布很快完成使得循環基本達到穩定狀態;而在0.08 kN(ζb=1.0)循環荷載作用下,轉動中心先是向下發展然后又向上發展。分析可知,砂土處于塑性階段,砂土顆粒重分布更加劇烈,循環需要達到穩定所以轉動中心向下發展。隨著循環次數的增加箱筒型防波堤基礎逐漸被向上拉起,導致轉動中心向上移動。
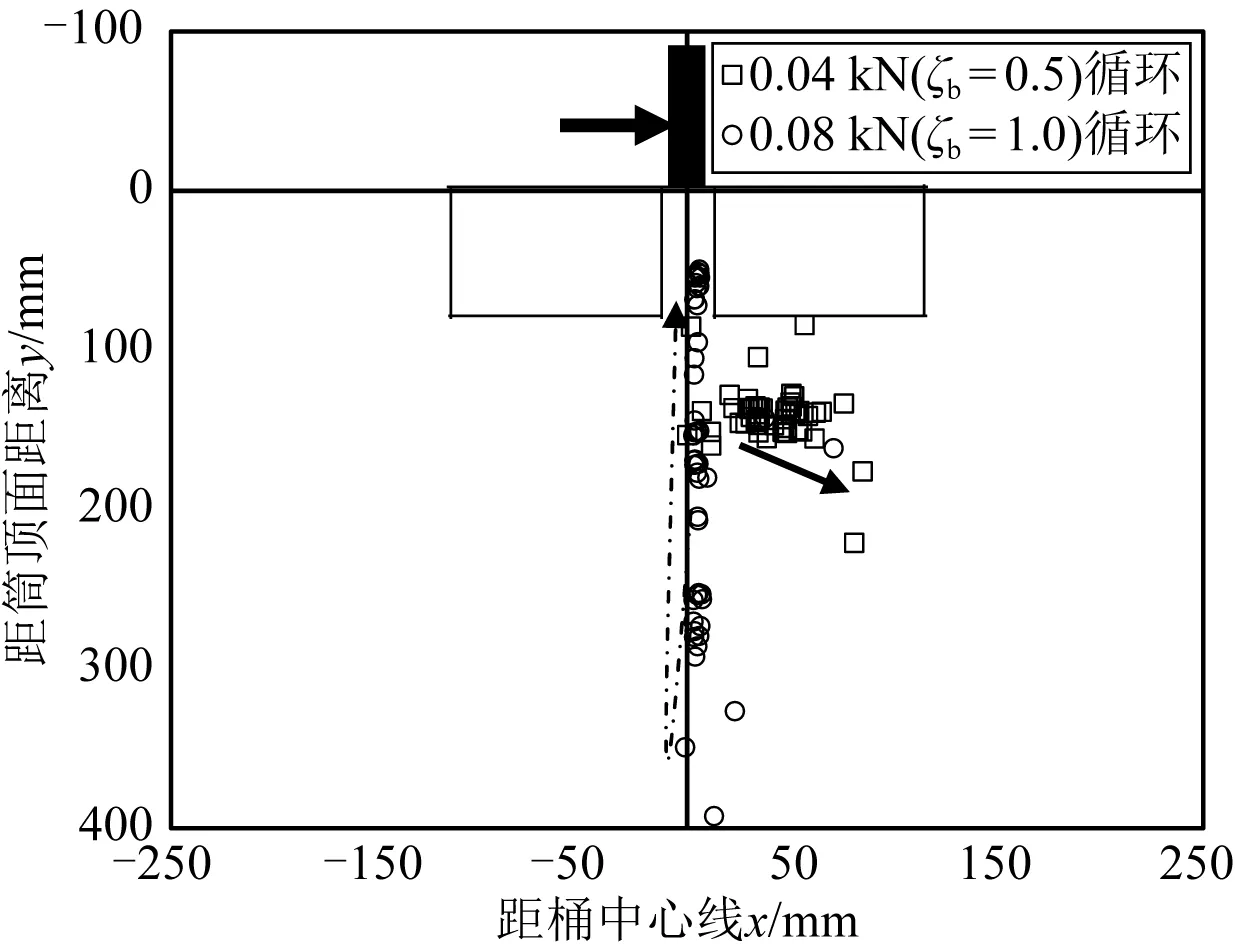
圖7 轉動中心與箱筒型基礎的位置關系Fig. 7 The positional relationship between the center of rotation and the box-type foundation
2.4 箱筒型基礎穩定性分析
文獻[19, 23]指出箱筒型防波堤基礎是屬于寬淺式的薄壁筒型結構物,其極限狀態下的運動模式不同于傳統的重力式結構,箱筒型防波堤基礎在處于極限平衡狀態時,轉動中心位于筒底以下某點處,而傳統重力式結構認為轉動中心處于結構的前腳趾處。以箱筒型防波堤基礎為研究對象,建立極限平衡分析模型,如圖8所示。需要說明的是,循環加載過程中土體實際是一直隨著循環次數變化的。為計算簡便,未考慮因循環次數增加導致土體狀態變化的特性。
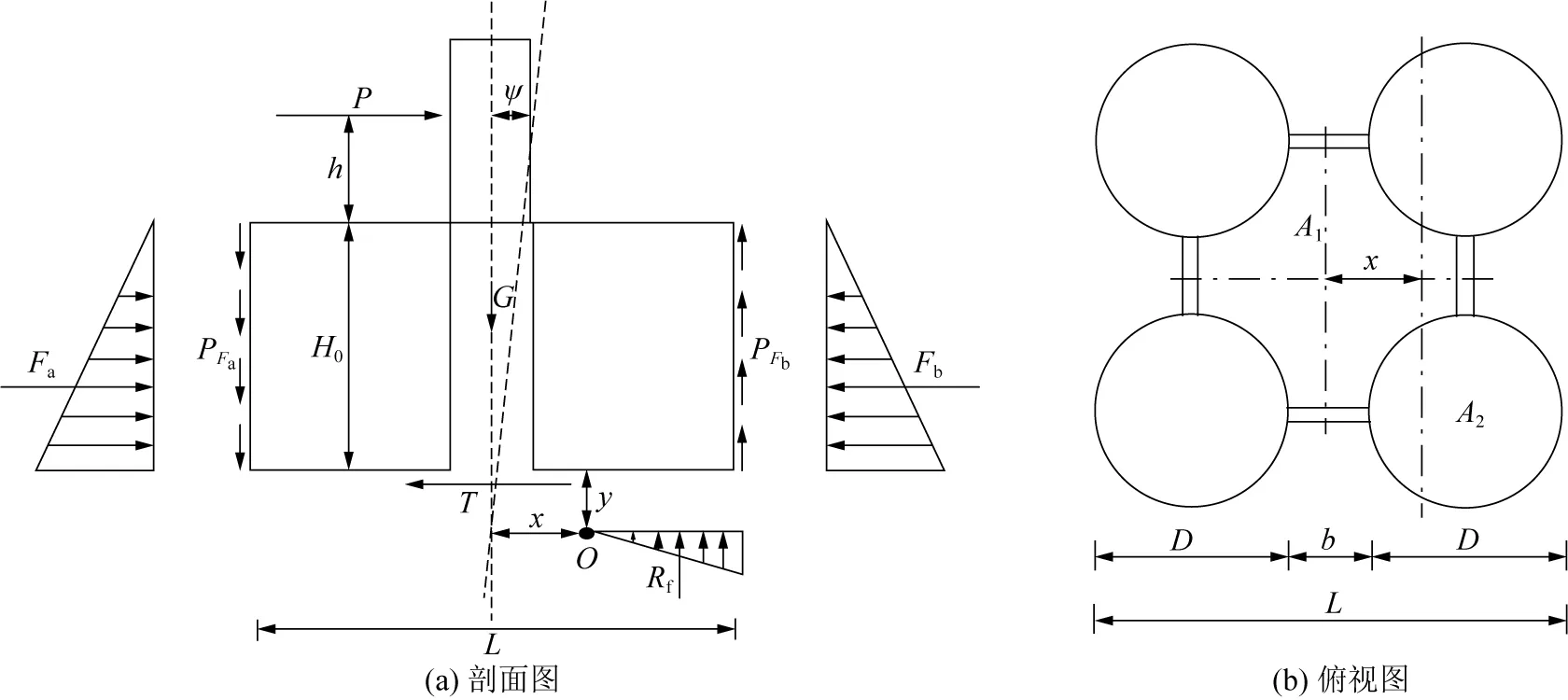
圖8 穩定性計算簡圖Fig. 8 Stability calculation diagram
作用在箱筒型防波堤基礎上的力可分為外加荷載、土壓力、結構自重、內外壁摩擦阻力、底部剪切力以及頂蓋和筒底受到的土反力。各個力對極限狀態時箱筒型防波堤的作用分析如下。
外力P對轉動點O的力矩MP為:
MP=P(h+H0+y)
(6)
式中:h為外力P到筒頂面的距離,H0為筒高,y為轉動點距離筒底的距離,取正值。
箱筒型防波堤基礎的自重所產生重力為G,為計算方便假設重心處于箱筒型防波堤幾何中心處,則重力G對轉動點O的力矩MG為:
MG=G[x-(H0/2+y)tanψ]
(7)
式中:x為轉動中心到筒中軸線的距離,其他符號意義同上。
假設砂土地基是均勻的,作用在箱筒型防波堤基礎上的任意一點處土壓力符合朗肯土壓力定律,則箱筒型防波堤基礎所受的主、被動土壓力合力Fa、Fb為:
Fa=1/2LηγH02Ka
(8)
Fb=1/2LηγH02Kb
(9)
式中:L為整體筒長,η為折減系數,根據文獻[12]中箱筒型防波堤土壓力性狀分析結果,建議η取值為0.6,γ為土的重度,Ka、Kb為朗肯主、被動土壓力系數。則主、被動土壓力Fa、Fb對轉動點O的力矩MFa、MFb為:
MFa=Fa(H0/3+y)
(10)
MFb=Fb(H0/3+y)
(11)
由于轉動中心位于筒底以下,則底部剪切力T的方向與外力P的加載方向相反,底部剪切力T對轉動點O的力矩MT為:
T=γH0tanψA1
(12)
MT=Ty
(13)
式中:A1為整個箱筒型防波堤基礎底面面積,其他符號意義同上。
箱筒型防波堤基礎的上部蓋板、筒底部和連接墻底部承受地基反力,結合試驗箱筒型防波堤基礎運動趨勢以及外力P的加載方向,當箱筒型防波堤基礎處于極限狀態時,因為轉動點左側土體已經與基礎上部蓋板分離,而土體與基礎只能受壓不受拉,所以只有轉動點O右側的蓋板、筒底部和連接墻底部受到地基反力,地基反力Rf對轉動點O的力矩MRf為:
Rf=1/2KV(L/2-x)tanψA2
(14)
MRf=2/3Rf(L/2-x)
(15)
式中:KV為豎向基床系數,根據文獻[24],砂土地基中建議取規范的下限值5 MN/m3,A2為轉動點右側底部面積,其他符號意義同上。
結合箱筒型防波堤基礎的運動模式,可知主動土壓力區摩擦力豎直向下,被動土壓力區的摩擦力豎直向上,主動、被動土壓力區的摩擦力PFa、PFb對轉動點O的力矩MPFa、MPFb為:
PFa=Fatanφ
(16)
PFb=Fbtanφ
(17)
MPFa=PFa(L/2+x)
(18)
MPFb=PFb(L/2-x)
(19)
式中:φ為砂土與樁界面摩擦角,其他符號意義同上。
箱筒型防波堤基礎在處于極限平衡狀態時應該滿足水平、豎向和彎矩平衡。
水平平衡方程為:
P+Fa-Fb-T=0
(20)
豎向平衡方程為:
G+PFa-PFb-Rf=0
(21)
彎矩平衡方程為:
MP+MFa-MG-MFb-MT-MRf-MPFa-MPFb=0
(22)
基于式(20)、(22)計算抗滑移抗系數K1為:
K1=(Fb+T)/(P+Fa)
(23)
抗傾覆系數K2為:
K2=(MG+MFb+MT+MRf+MPFa+MPFb)/(MP+MFa)
=[(G-2/3Rf+PFa-PFb)x+(Fb+T-Gtanψ)y+(FbH0/3+2/3RfL/2+PFaL/2+PFbL/2-
GH0tanψ/2)]/[(Fa+P)y+(Ph+PH0+FaH0/3)]
(24)
式中:x、y可由式(4)、(5)計算得出。
箱筒型防波堤基礎的穩定性設計應該是以K1、K2中較小值為依據。當K1>K2時,箱筒型防波堤基礎首先發生滑移破壞;當K1 表2 穩定系數與循環次數的關系Tab. 2 The relationship between the stability coefficient and the number of cycles 通過箱筒型防波堤基礎室內模型試驗,對箱筒型防波堤基礎轉動中心、水平循環累計位移、抗滑移抗傾覆穩定性進行研究,得出以下結論: 1) 通過荷載位移曲線出現明顯拐點確定箱筒型防波堤基礎極限承載力為0.08 kN,并且荷載位移曲線可以分為準彈性階段、塑性階段、破壞階段,相應的基礎運動模式為水平滑動為主、水平滑動和轉動、轉動為主。 2) 箱筒型防波堤基礎在受到ζb=0.5、ζb=1.0水平循環荷載作用時,以前10次累計位移最為明顯,分別占總循環累計位移的96.70%、91.88%,這是因為土體發生剪脹,土顆粒重新排列;而后40次循環累計位移不明顯,分別占總循環累計位移的3.30%、8.12%,是因為此時土體發生剪縮,土顆粒之間致密化。 3) 箱筒型防波堤基礎是一種寬淺式基礎,其轉動中心位于筒底以下某點處,在循環荷載作用下的轉動中心是變化的,為保持其穩定性,轉動中心有向下運動的趨勢。 4) 箱筒型防波堤基礎以ζb=0.5水平循環荷載作用時,穩定系數K1、K2均大于1,即說明在循環過程中穩定性良好不易發生滑移與傾覆破壞;在以ζb=1.0水平循環荷載作用時,穩定系數K1、K2均小于1并且K1大于K2,即說明在循環過程中基礎會首先發生滑移破壞進而發生嚴重的傾覆破壞。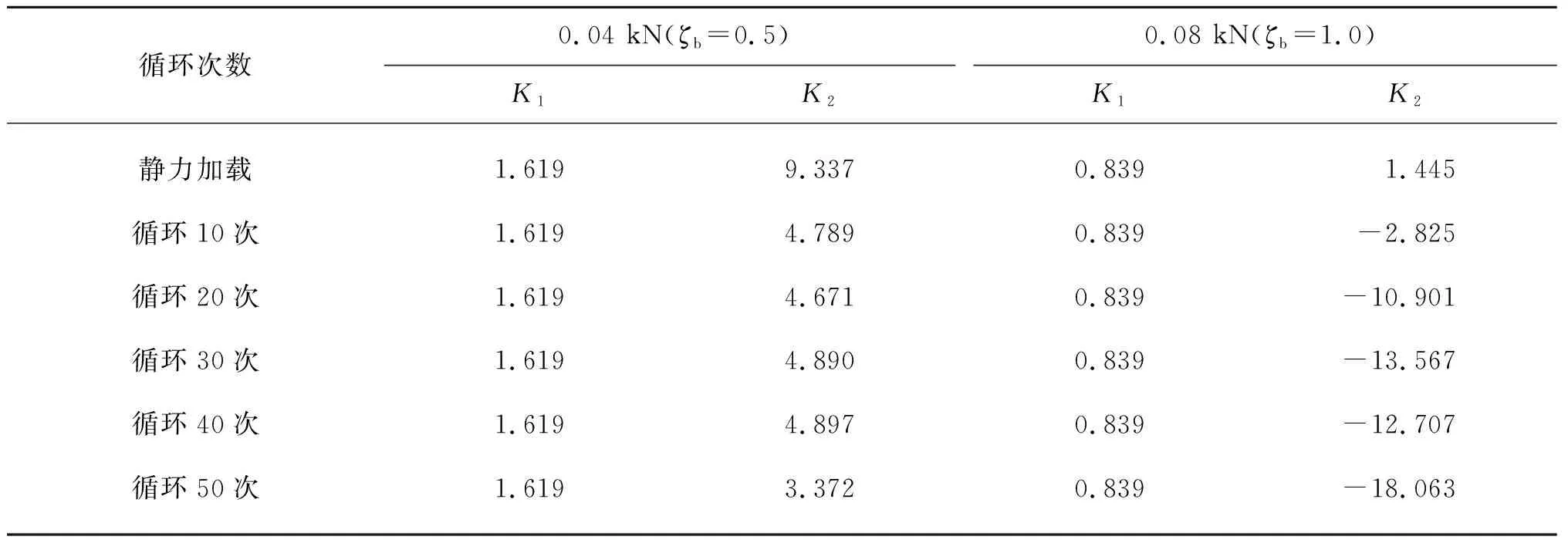
3 結 語

