基于時變內力加權指標的大型冷卻塔等效靜風荷載

趙林 陳旭 展艷艷 葛耀君

摘要： 等效靜風荷載是對動態風荷載和結構慣性力的擬靜力化等價荷載模式，涵蓋結構預期動力響應包絡值，屬結構設計中的荷載效應簡化分析環節。在大跨空間結構抗風設計中，等效準則選取與荷載模式識別是將復雜動力問題轉化為擬靜力問題的關鍵步驟。目前等效靜風荷載的評價準則眾多，不同準則下的等效模式差異明顯，缺少統一的共識性標準。為了體現不同風致內力響應對結構安全的綜合影響，將評價準則由單一的荷載或內力層面拓展到多種內力加權組合層面。對于鋼筋混凝土空間結構，該準則以物理概念清晰的配筋率作為表現形式，并融入結構動力響應時變特征。以某大型冷卻塔為例，在脈動風壓加載條件下進行時域分析得到風致結構動力響應時程，根據時變內力加權組合計算結構動態配筋率;從單一內力和內力加權兩個層面評價現行規范等效靜風荷載的抗風安全冗余度;以配筋包絡線為等效目標，反演獲得了兼顧多種內力加權組合的等效靜風荷載分布模式，闡明了相關算法和等效策略的合理性和工程適用性。

關鍵詞： 大跨空間結構; 風荷載; 大型冷卻塔; 時變內力加權組合; 動態配筋包絡

中圖分類號： TU393.3; TU312+.1 文獻標志碼： A 文章編號： 1004-4523（2021）05-0922-12

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.005

1 背 景

風荷載為引起結構動力響應的隨機動態荷載。結構風致響應分析時常把風荷載人為地劃分為平均分量和脈動分量，并分別考慮其對結構的作用。針對冷卻塔這類高聳薄壁空間結構，國內外學者通過現場實測[1?2]和風洞試驗[3?4]研究了表面平均風壓和脈動風壓分布規律及其對結構響應的影響[5?6]。實際工程應用中為簡化分析計算過程[7]，引入了等效靜風荷載概念，即在平均風壓的基礎上進行放大或修正以考慮荷載脈動引起的風振效應，從而將動力問題轉化為靜力問題。該策略也是世界各國制定以冷卻塔為代表的大跨空間結構風荷載規范條款的重要依據[8?9]。

等效靜風荷載理論研究中最具代表性的為Davenport[10]于1967年提出的GLF（Gust Loading Factor）方法以及Kasperski等[11]于1992年提出的LRC（Load Response Correlation）方法。其中，基于GLF法的等效靜風荷載被編入包括中國在內的許多國家的建筑結構設計規范[12]，LRC法亦被澳大利亞等一些國家的規范所采用[13]。后續學者在此基礎上不斷改進，針對不同結構類型提出了風荷載作用下與等效目標匹配的等效靜風荷載模型（詳見表1）[10?11，14?20]。上述等效靜風荷載模型的等效目標眾多，如薄膜力、位移、彎矩等，當結構存在多個控制目標時難以同時考慮或滿足。為解決此類多目標等效問題，Katsumura等[16]首次提出了全局等效風荷載理論，等效靜風荷載模型逐漸從僅關注特定部位極值響應的單目標等效向包絡所有單元結構效應極值的多目標等效的趨勢發展。

等效靜風荷載分布模式與等效目標評價準則息息相關，不同評價準則各有適用性且難于同時兼顧，具體表現為：同一結構不同構件的控制內力不同，相同構件不同加載條件下的控制內力也不同，難以評價不同準則的優劣;結構的整體強度、剛度和穩定性由不同響應共同決定，以單一結構響應為目標建立的等效靜風荷載分布模式難以兼顧整體最不利情況;而多目標全局等效靜風理論更多地體現為數學意義上的統一擬合優化策略，無法明確氣動力等效分布模式的物理意義。針對上述問題，本文提出基于時變內力加權組合的等效靜風荷載評價準則;與以往單一的評價準則相比，該準則是風荷載作用下結構所有內力指標的匯總和深化，能考慮不同內力對結構安全的綜合貢獻，而不拘泥于追求對某一特定響應的等效。實際工程應用中鋼筋混凝土結構的內力加權組合可體現為配筋量，鋼結構的內力加權組合可體現為構件截面尺寸，這種對應關系為該評價準則的實際應用奠定了基礎。Zhao等[20?22]已結合此概念進行了群塔干擾條件僅考慮冷卻塔平均風壓作用下靜態內力加權的等效風荷載研究，初步證明了其有效性和可行性。本文將在此基礎上，進行動態風壓作用下的動力效應分析，探究動力響應條件下的風荷載等效模式。與前人研究的主要區別為：不再將動態風壓拆分為平均部分和脈動部分，即不再根據平均風壓和風振系數計算風致響應;而是將動態風壓作用下結構效應時域分析的概念進一步推廣到結構配筋響應層面。該過程綜合了靜、動態荷載分布模式和結構效應綜合貢獻，避免了現有規范中基于特定效應的風振系數簡化近似處理方式，物理概念更加明確。

在上述思路的指導下，以某大型冷卻塔為實例，確定如下研究方案（如圖1所示）：實施剛體模型測壓風洞試驗，獲得塔筒內、外表面動態風壓時程;加載脈動風荷載，進行結構動力響應有限元分析，獲得結構內力響應時程;根據時變內力加權組合進行結構強度設計，得到動態配筋時程和配筋包絡曲線;從單一內力和不同內力加權組合等多個角度，評價現行規范二維風壓分布模式的抗風安全冗余度及不同評價指標的適用性;以配筋包絡曲線為等效目標，根據風洞試驗風壓系數均值和標準差，提出新的等效靜風荷載分布模式，并驗證其有效性。

2 概念說明

2.1 內力加權組合與結構配筋

內力加權組合反映了不同內力對結構安全的綜合影響，由于不同類別的內力具有不同的物理意義和單位，很難通過數值大小直接評價其在結構安全中的地位，也不能簡單通過數值加權組合體現之間的共同作用。鋼筋混凝土結構中的配筋設計為實現內力的合理加權組合及確定物理意義清晰的量化指標提供了參考依據，內力加權組合系數并非取自經驗參數組合，而是借助半理論半經驗的結構配筋計算實現;量化指標不是直接加權組合后的數值大小，而是構件的配筋量。通過這種方式，將不同單位、不同物理意義的內力轉換成能夠直接量化比較的配筋率。

根據《混凝土結構設計規范》GB 50010?2010[23]，結構構件的配筋面積由材料特性（）、單元尺寸（）和內力大小（）共同決定。對于鋼筋混凝土超大型冷卻塔，風荷載是塔筒結構設計的控制荷載，塔筒配筋設計分別在環向和子午向的內、外表面進行，共有四類配筋（如圖2所示），即子午向外側鋼筋（MO）、子午向內側鋼筋（MI）、環向外側鋼筋（CO）和環向內側鋼筋（CI）。動態風壓作用下，內力隨時間變化，對應地可以得到隨時間變化的配筋結果

上述塔筒殼體單元從內力到配筋過程可按照《混凝土結構設計規范》GB 50010?2010[23]中的偏心受力構件配筋，求解配筋率的主要公式如下：

式中 為符合大偏心受壓單元的軸力，為符合小偏心受壓單元的軸力，為單元所受彎矩，為選用混凝土的抗壓強度，為截面寬度，計算中長度取1 m，與分別為受拉與受壓鋼筋的強度設計值，則為考慮鋼筋沒有到達強度設計值時的應力，為截面受壓區有效高度，根據不同位置處壁厚換算得到，為鋼材的彈性模量，為鋼材的極限應變，為相對受壓區高度，為單元外側的配筋量，為單元內側的配筋量，將計算所得每延米范圍內的配筋面積定義為單元配筋量，單元配筋量按不同方向內外側共有四種類型，即環向外側、環向內側、子午向外側、子午向內側。

由于風向的不確定性以及冷卻塔塔筒結構的旋轉對稱特性，實際設計時同一高度處僅取一組配筋結果用于所有環向構件，形成沿塔筒高度方向變化的四類配筋包絡線。該設計過程涵蓋塔筒單元配筋動態時程的兩次包絡環節：

第一次是時間配筋包絡，即針對計算時間段內的每個塔筒單元分別取具有一定概率保證率的配筋極值，獲得空間三維時間配筋包絡面，該極值可以簡化為均值+峰值因子×均方根，高斯過程下當峰值因子取3.5，可獲得具有99.5%概率保證率的極值[24]，如下式

式中 為單元的配筋包絡值，為單元配筋量在時程上的均值，為單元配筋量在時程上均方差，為時程參數，為環向角度參數，為高度項參數，為峰值因子，取3.5。

第二次為空間配筋包絡，即針對時間配筋包絡面在塔筒同一高度取最大值，得到沿高度變化空間配筋包絡線，如下式

式中 為將各風向角下結果沿環向取極值的過程函數，本文以單塔為例，考慮結構和荷載的對稱性，僅需單一風向角。

下文內力和配筋包絡線均建立在此方法基礎上。

2.2 規范風壓分布

冷卻塔結構設計規范《火力發電廠水工設計規范》（DL/T5339?2018[25]，后文簡稱《水工規范》）中采用“靜態風壓×風振系數”考慮風對結構的作用，對應的塔筒外表面等效靜風荷載定義如下

式中 為作用在塔筒外表面等效風荷載標準值;為風振系數，B類地貌取1.9;為群塔干擾系數，單塔取1;為風壓高度變化系數;為基本風壓;為子午向高度;為環向角度;為平均風壓體型系數，外表面平均風壓分布如下式所示

式中 為項數，無肋雙曲冷卻塔取7;為系數，無肋塔?取值分別為-0.4426，0.2451，0.6752，0.5356，0.0615，-0.1384，0.0014，0.0650。

塔筒內表面風壓沿環向和子午向均勻分布，等效靜風荷載定義如下：

式中 為內吸力標準值;為內吸力系數，取-0.5;為塔頂風壓設計值;為塔頂標高處風壓高度變化系數;與外壓相同，為基本風壓。

下文研究的單塔等效靜風荷載采用無量綱風壓形式，對應式（8）與（10）中考慮風振效應的內、外表面風壓體型系數的合量。

3 風洞試驗及有限元分析

3.1 風洞試驗

原型冷卻塔結構高185 m，塔頂直徑82.5 m，喉部高度156.8 m，喉部直徑79.2 m，通風口離地高度27.5 m，塔筒底部直徑126.8 m，通風筒殼體沿高度指數變厚，喉部最小壁厚0.25 m，下環梁最大壁厚1.75 m，塔筒由48對直徑為1.8m的X型柱支撐，塔筒直徑和壁厚沿高度分布如圖3所示。

綜合考慮結構尺寸、風洞試驗段大小、阻塞率和雷諾數效應模擬等因素，冷卻塔剛性測壓模型幾何縮尺比為1∶300，對應的風洞阻塞率為0.7%<5%。模型內、外表面沿高度方向分別布置4層和12層測壓點，每層均勻布置36個測點，共計布置12×36=432個外壓測點，4×36=144個內壓測點（如圖4所示）。冷卻塔這類圓截面結構表面繞流特性對雷諾數效應非常敏感，本文通過控制風速和改變模型表面粗糙度相結合的方法實現亞臨界雷諾數下模擬高超臨界鈍體繞流特征[26]。其中，通過在塔筒外壁粘貼不同層數的粗糙紙帶來調節模型表面粗糙度，每層粗糙紙帶寬10 mm，厚0.1 mm。雷諾數模擬標準為《水工規范》[25]建議的原型冷卻塔外表面平均風壓實測曲線和Zhao[2]等基于大型冷卻塔實測的脈動風壓分布曲線。當冷卻塔外表面粘貼4層紙帶時，雷諾數效應模擬效果最好，補償后的塔筒外壓系數均值和脈動值分布如圖5所示。

剛體模型測壓風洞試驗在同濟大學土木工程防災國家重點實驗室TJ?3大氣邊界層風洞中進行，該風洞為閉口回流式矩形截面風洞，試驗段寬15 m、高2 m、長14 m，風速調節范圍為0?17.6 m/s。試驗中利用尖劈和粗糙元模擬B類地貌風場，風速比為1∶5，模擬的平均風剖面、紊流度和順風向風譜與規范吻合良好[12]（如圖6所示）。

3.2 有限元分析

冷卻塔建模時塔筒離散為空間殼Shell63單元，X型支柱和環基采用空間梁Beam188單元[27]，支柱底與環基剛性連接。塔筒沿高度劃分為55層，從塔底到塔頂依次編號L1?L55，第53和54層分別為塔頂剛性環的裙板和豎板，每層沿環向均勻劃分96個單元，支柱劃分為96個單元，環基劃分為144個單元;塔筒和支柱采用C40混凝土，環基采用C30混凝土;建模效果和結構動力特性如圖7和表2所示。

為了研究風荷載作用下的結構響應，加載的風荷載分別來源于風洞試驗的動態風壓時程和《水工規范》 [25]定義的B類地貌下無肋雙曲等效靜風荷載（見式（2）?（5）），設計基本風速均取50 m/s。動態風壓時域分析中，使用本征正交分解法（POD法）[28]將塔筒內、外表面風壓測點拓展至與有限元模型對應的56×96個節點。圖8以塔筒中部第20層單元（L20）迎風駐點的子午向軸力和子午向外側配筋為例，展示結構內力時程、配筋時程和對應的概率包絡值，其中的配筋率最小值由規范[23]最小配筋率控制。

4 等效準則

4.1 單一風致內力準則

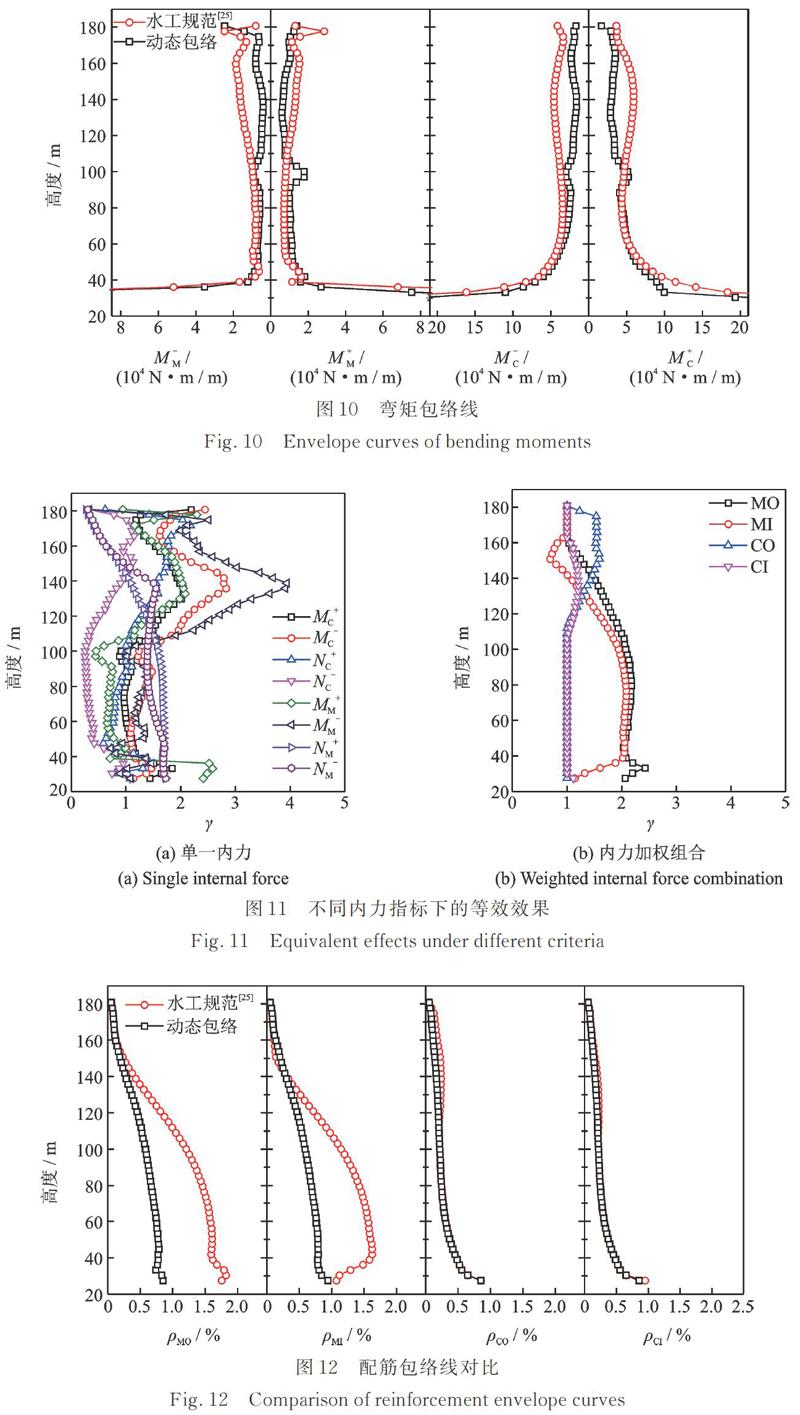
風致內力是目前等效靜風荷載等效效果評價的主要依據，分別選取子午向軸力、環向軸力、子午向彎矩和環向彎矩的包絡曲線對比規范風壓[25]和動態風壓對不同內力的等效效果（如圖9?10所示）;其中，規范風壓下的內力包絡線取同一高度環向所有單元內力分析的極值，動態風壓下的內力包絡線則根據3.1節的方法確定。為量化兩者差異，定義等效比例系數如下

式中 為等效比例系數，即規范風壓和試驗動態風壓下的響應包絡的比值。和分別為規范風壓和試驗動態風壓下響應包絡值。

由于動態包絡值源于脈動風荷載動力配筋計算，規避了風振系數這類簡化處理，更接近真實情況，因此作為比較的參照標準;說明規范等效靜風荷載存在一定的冗余度;說明規范等效靜風荷載不能保證結構的安全;說明等效效果較好，同時兼顧結構經濟性和安全性。

圖9和10分別給出了兩種風壓模式下軸力和彎矩響應包絡隨塔筒高度的變化。對于風荷載作用下的主要控制內力——子午向軸力：塔筒喉部以下，規范風壓在塔筒中下部可以完全涵蓋動態風壓包絡值，并存在一定冗余，最大值冗余度為70%;塔筒喉部以上，規范值不能完全包絡動力分析結果，但二者差異較小。對于數值較小的環向軸力：環向壓力在喉部以下，規范值小于動力包絡值，在喉部以上規范值與動力包絡值差異較小;環向拉力在喉部以下，兩類風壓模式下的結果較為接近，在喉部以上規范值有冗余。對于子午向和環向彎矩和，兩類風壓模式下的計算結果在塔筒中下部差異較小，在喉部附近規范值具有較高的冗余度。由單一內力的等效比例系數可見（如圖11（a）所示）：不同種類內力之間，甚至是同種類別不同方向的內力之間，比例系數沒有確定的分布規律，這反映出冷卻塔結構風致響應的復雜性，以不同類型內力為標準建立的等效靜風荷載模式將存在較大差異;內力層面相對無序的分布規律也證明了尋找同時滿足所有內力等效的多目標等效風荷載分布模式是極其困難的。圖11（b）給出的基于內力加權組合的等效比例系數分布規律簡潔明了，這為下一步的等效荷載分布模式研究提供了便利，尤其在喉部區域附近，四個指標的差異顯著，應重點關注。

4.2 內力加權組合準則

圖12對比了基于試驗風荷載動力分析獲得的時變加權內力的配筋包絡值與規范等效靜風荷載作用下的塔筒配筋值，可以看出：對于環向內、外側配筋和，兩種風壓分布模式下的結果非常接近，差別主要體現在喉部附近，這是由于冷卻塔沿環向配筋量較少，多數情況下由最小配筋率控制，風荷載模式差異不會引起配筋量的顯著變化。兩種風壓模式結果的差異主要表現在子午向配筋和，規范值在塔筒中下部大于動態包絡值，存在過高的安全儲備，最大冗余度可超過50%;但在喉部附近，規范風荷載作用下的子午向內側配筋數量不足，存在安全風險隱患。

5 等效靜風荷載

5.1 改進算法理論

由上節可知，無論是以單一內力作為等效目標，還是以內力加權組合作為等效準則，目前水工規范[25]中等效靜風荷載整體安全儲備過高，但在塔筒喉部等局部薄弱位置又存在安全隱患，有必要提出新的等效靜風荷載分布模式來兼顧結構安全性和經濟性。由于以單一風致內力為目標的等效效果差異顯著，導致基于不同種類內力作為等效準則的風荷載分布模式可能存在較大差異;而基于內力加權組合的配筋包絡作為等效模式物理意義明確，分布規律簡潔明了、趨勢性強，故將其作為本節的等效目標。

風荷載作用下結構動力響應極值可以表示如下

式中 為設計動力響應極值，為響應空間線性無關的一組基向量，為組合系數向量，為由組成的矩陣，也稱為標準響應，可表示為如下形式

式中 即為作用在結構上的等效靜風荷載向量，該向量是荷載矩陣中每一列荷載向量的線性組合。

本文等效靜風荷載模式的反演以風洞試驗的動態風壓為基礎，將荷載的平均值和標準差作為荷載矩陣的基向量進行線性組合，整個過程包含等效風壓系數基線確定以及塔筒高度調整系數選取兩個環節。

5.2 風壓模式反演

（1）等效風壓系數基線確定：對塔筒不同高度處風壓系數平均值和標準差的極值和組成的曲線集合取上、下包絡線Line1和Line2;分別在0°?90°及270°?360°的正壓區（Zone1）選用Line1，在90°?270°負壓區（Zone2）選用Line2;3段曲線相連，得到組合曲線。由于單塔風壓分布的對稱性，圖13僅給出了0°?180°結果，180°?360°結果根據對稱原則鏡像;采用下式所示三角級數多項式對上述曲線組合進行擬合得到等效風壓系數基線，擬合系數如表3所示。

（2）塔筒高度調整系數選取：由于塔筒不同高度安全冗余情況不同，沿塔筒高度取不同調整系數對等效風壓系數基線進行放大或縮小

式中 為調整后的等效風壓系數，為塔筒高度調整系數，為沿塔筒子午向高度。

本例中，塔筒上部1/3以上高度，調整系數取1.2，塔筒下部2/3以下高度取0.8。如下式所示

式中 為塔筒總高度。

沿高度方向調整后的等效風壓分布曲線與規范風壓相比具有以下特點：沿子午向分段變化，沿環向平緩變化;正壓極值增大，負壓極值減小，如圖14所示。

5.3 等效效果對比

圖15給出了本文提出的等效靜風荷載、規范等效靜風荷載和風洞試驗動態風壓作用下的子午向和環向內、外側，，，四類配筋的包絡值;并以動態包絡作為精確解，對比了本文等效靜風荷載和規范等效靜風荷載的等效效果如圖16所示。圖16中，γMO，γMI，γCO和γCI分別表示子午向外側、子午向內側、環向外側、環向內側配筋包絡的等效比例系數。可以看出：本文提出的等效風荷載分布模式能夠顯著降低塔筒子午向配筋量，尤其是塔筒中下部，顯著改善了結構抗風安全冗余度;環向配筋在大多數塔筒位置仍由最小配筋率控制，風壓分布模式的改變未對其造成明顯的影響;但在喉部附近子午向配筋無法實現包絡（圖16中處于陰影區域的點），說明了塔筒喉部是冷卻塔研究、設計和建造中重點關注的部位，必要條件下應需采取局部加強措施。

圖17對比了3種風荷載分布模式下四類配筋用量和鋼筋總用量。其中，本文提出的等效靜風荷載所需鋼筋總量與動態包絡結果非常接近，但相比規范風壓鋼筋總用量減小約33%，顯著提高了經濟性。由于文中僅考慮了風荷載作用效應，并且只統計了上部塔筒結構，該值約為實際工程的1/3。

6 結 論

通過剛體模型測壓風洞試驗、結構有限元計算和動態配筋設計，分析了風荷載作用下的鋼筋混凝土冷卻塔單元內力和內力加權組合的分布規律;評價規范等效風荷載模式在單一內力層面和內力加權組合層面的等效效果和抗風安全冗余度;提出基于配筋包絡指標的等效靜風荷載分布模式，并對其等效效果進行驗證。主要結論如下：

（1）同一等效靜風荷載模式在不同內力指標下的等效評價效果差異顯著，而基于時變內力加權指標的等效效果更具統一、簡潔的分布規律;

（2）內力加權指標能夠考慮不同內力對結構安全的綜合影響且與實際工程應用緊密結合，推薦為等效風荷載的評價指標;

（3）從結構配筋的角度，現行水工規范的等效靜風荷載存在較高的冗余度，主要表現在塔筒中下部，并在塔筒喉部位置附近存在安全儲備不足的隱患;

（4）基于內力加權指標的等效風荷載分布模式以風洞試驗風壓系數均值和標準差為基礎，能夠較好地擬合塔筒配筋包絡曲線，與規范風壓模式相比，兼顧了抗風安全性和結構經濟性。

本文以單塔工況為例梳理了相關概念和方法，群塔干擾工況時等效靜風荷載分析流程不變，僅需根據干擾下的風壓分布模式調整等效風壓系數基線以及改變沿塔高的調整系數，后續將對復雜群塔組合工況開展更廣泛的研究，驗證提出的等效靜風荷載模式的適用性。

參考文獻：

[1] Pirner M. Wind pressure fluctuations on a cooling tower[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1982， 10（3）： 343-360.

[2] Zhao L， Ge Y J， Kareem A. Fluctuating wind pressure distribution around full-scale cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2017， 165：34?45.

[3] 李鵬飛， 趙 林， 葛耀君，等. 超大型冷卻塔風荷載特性風洞試驗研究[J]. 工程力學， 2008， 25（6）： 60-67.

Li P F， Zhao L， Ge Y J， et al. Wind tunnel investigation on wind load characteristics for super large cooling towers[J]. Engineering Mechanics， 2008， 25（6）： 60-67.

[4] Armit J. Wind loading on cooling towers[J]. Journal of the Structural Division， 1980， 106（3）： 623-641.

[5] Kasperski M， Niemann H J. On the correlation of dynamic wind loads and structural response of natural-draught cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1988， 30（1-3）： 67-75.

[6] Sollenberger N J， Billington D P， Scanlan R H. Wind loading and response of cooling towers[J]. Journal of the Structural Division， 1980， 106（3）： 601-621.

[7] Davenport A G. How can we simplify and generalize wind loads？[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1995， 54（94）： 657-669.

[8] VGB-R610ue. VGB-Guideline： Structural design of cooling tower-technical guideline for the structural design， computation and execution of cooling tower[S]. Essen： BTR Bautechnik bei Kühltürmen， 2005.

[9] BS4485. Code of practice for structural design and construction[S]. London： British Standard Institution， 1996.

[10] Davenport A G. Gust loading factors[J]. Journal of the Structural Division， 1967， 93（ST3）： 11-34.

[11] Kasperski M， Niemann H J. The L.R.C. （load-response-correlation）?method a general method of estimating unfavourable wind load distributions for linear and non-linear structural behaviour[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1992， 43（1-3）： 1753-1763.

[12] 中華人民共和國住房與城鄉建設部.GB 50009-2012， 建筑結構荷載規范[S]. 北京： 中國建筑工業出版社， 2012.

MOHURD. GB50009-2012， Load code for the design of building structures[S]. Beijing： China Architecture & Building Press， 2012.

[13] Australia Standard. Amendment 1 to AS/NZS 1170.2：2002 - Structural Design Actions - Part 2： Wind Actions[S]， 2002.

[14] Holmes J D. Effective static load distributions in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2002， 90（2）： 91-109.

[15] Kareem A， Zhou Y. Gust loading factor—Past， present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2003， 91（12）： 1301-1328.

[16] Katsumura A， Tamura Y， Nakamura O. Universal wind load distribution simultaneously reproducing largest load effects in all subject members on large-span cantilevered roof[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2007， 95（9-11）： 1145-1165.

[17] Ke S T， Ge Y J， Zhao L， et al. A new methodology for analysis of equivalent static wind loads on super-large cooling towers[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2012， 111： 30-39.

[18] Blaise N， Deno?l V. Principal static wind loads[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2013， 113： 29-39.

[19] Yang Q， Chen B， Wu Y， et al. Wind-induced response and equivalent static wind load of long-span roof structures by combined Ritz-proper orthogonal decomposition method[J]. Journal of Structural Engineering， 2013， 139（6）： 997-1008.

[20] Zhao L， Zhan Y Y， Ge Y J. Wind-induced equivalent static interference criteria and its effects on cooling towers with complex arrangements[J]. Engineering Structures， 2018， 172： 141-153.

[21] Yu M， Zhao L， Zhan Y Y， et al. Wind-resistant design and safety evaluation of cooling towers by reinforcement area criterion[J]. Engineering Structures， 2019， 193： 281-294.

[22] Zhao L， Chen X， Ge Y J. Investigations of adverse wind loads on a large cooling tower for the six-tower combination[J]. Applied Thermal Engineering， 2016， 105： 988-999.

[23] 中華人民共和國住房與城鄉建設部. GB 50010-2010， 混凝土結構設計規范[S]. 北京： 中國建筑工業出版社， 2010.

MHOURD. GB50010-2010， Code for design of concrete structures[S]. Beijing： China Architecture & Building Press， 2010.

[24] 張相庭. 結構風壓與風振計算[M]. 上海： 同濟大學出版社， 1985.

Zhang X T. Structural Wind Pressure and Calculation of Wind-Induced Vibration[M]. Shanghai： Tongji University Press， 1985.

[25] 電力規劃設計總院. DL/T 5339-2018， 火力發電廠水工設計規范[S]. 北京： 中國計劃出版社， 2018.

China Electric Power Planning & Engineering Institute. DL/T 5339-2018， Code for hydraulic design of fossil fired power plant[S]. Beijing： China Planning Press， 2018.

[26] Kareem A， Cheng C M. Pressure and force fluctuations on isolated roughed cylinders of finite height in boundary layer flows[J]. Journal of Fluids and Structures， 1999， 13（7）： 907-993.

[27] 王新敏， 李義強， 許宏偉. Ansys結構分析單元與應用[M]. 北京： 人民交通出版社， 2011.

Wang X M， Li Y Q， Xu H W. Ansys Structural Analysis Element and Application[M]. Beijing： China Communication Press， 2011.

[28] Tamura Y， Ueda H， Kikuchi H， et al. Proper orthogonal decomposition study of approach wind-building pressure correlation[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1997， 72： 421-431.

作者簡介： 趙 林（1974-），男， 教授，博士生導師。電話：（021）65984882;E-mail：zhaolin@tongji.edu.cn

通訊作者： 陳 旭（1988-），男，講師。電話：（021）57125281;E-mail：chenxu@shnu.edu.cn