相關熵和雙譜分析齒輪故障診斷研究

李輝 郝如江

摘要： 相關熵為高斯、非高斯噪聲處理的一種有效方法，針對強高斯噪聲和非高斯噪聲干擾下齒輪故障診斷問題，提出了一種基于相關熵和雙譜的齒輪故障診斷方法。該方法綜合利用高斯核函數和不完全Cholesky分解算法計算信號的相關熵，然后再計算相關熵的雙譜，根據相關熵的雙譜特征識別齒輪故障。通過不完全Cholesky分解算法計算信號的相關熵，不僅大大壓縮了數據量，突出了齒輪故障特征，而且提高了計算效率。通過仿真和齒輪磨損故障振動信號分析結果表明：強背景噪聲會造成傳統雙譜故障診斷方法失效，而基于相關熵和雙譜分析的齒輪故障診斷方法，能在強噪聲干擾背景中提取齒輪的故障特征準確識別齒輪故障，其性能優于傳統雙譜和小波變換域雙譜，為一種有效的齒輪故障診斷方法。

關鍵詞： 故障診斷; 齒輪; 信號處理; 相關熵; 雙譜

中圖分類號： TH165+.3; TH132.41; TN911.72 文獻標志碼： A 文章編號： 1004-4523（2021）05-1076-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.022

引 言

齒輪是機械傳動中最重要、最常用的零件之一，齒輪的健康狀態是保證機械傳動正常運行的重要因素，因此，基于振動信號的齒輪狀態監測是一個廣泛研究的課題[1?2]。當齒輪出現表面點蝕、齒根裂紋、斷齒等故障時，使得振動信號產生復雜的幅值、相位調制現象，不僅具有非線性、非高斯信號特征，而且往往包含大量的背景噪聲，將齒輪故障特征淹沒，這些因素加大了齒輪故障診斷的難度。振動信號的非線性、非高斯特征使傳統基于信號二階統計量的方法，如相關分析、功率譜分析等性能衰退，甚至失效[3?4]。基于信號高階統計量的信號處理方法，如雙譜[5?6]、切片雙譜[7]、倒雙譜[8]、循環雙譜[9?11]、高階譜[12]分析等則在非線性、非高斯信號處理方面有著獨特優勢，已廣泛應用于齒輪故障特征識別，取得了良好效果。鄭海波等[13]研究了汽車變速箱齒輪振動信號的雙譜和雙相干譜特征，并利用BP神經網絡成功將齒輪正常信號、磨損信號和斷齒信號進行了分類。周雁冰等[14]針對裂紋故障導致齒輪振動信號非高斯性變化的特點，提出了基于雙譜熵的齒輪裂紋故障特征提取方法。程軍圣等[15]綜合利用基于B樣條的局部特征尺度分解方法和雙譜分析識別齒輪裂紋故障。李學軍等[16]綜合利用聚類分析和雙譜技術實現了對齒輪正常、齒面點蝕、斷齒的模式識別與故障診斷。

齒輪故障振動信號呈周期性重復沖擊和復雜調制的特點，具有明顯的非平穩、非線性、非高斯特點。雙譜是分析高斯信號的有力工具，理論上能完全抑制高斯噪聲，但對非高斯類噪聲卻無能為力，信號中存在非高斯噪聲會對雙譜造成干擾。因而在強非高斯噪聲背景下，基于傳統雙譜的齒輪故障特征提取方法難以取得理想效果。相關熵是處理非高斯噪聲的有效方法，已在雷達和通信信號檢測、信號濾波、波達方向估計和時延估計等方面得到應用和驗證，取得了良好效果[17?19]。盡管相關熵方法在通信領域的應用已經展開，但在機電設備故障診斷領域的應用還未涉及。本文針對傳統雙譜難以有效處理強非高斯噪聲干擾的問題，綜合利用相關熵和雙譜的優點，提出了基于相關熵和雙譜的齒輪故障診斷方法。該方法綜合利用高斯核函數和不完全Cholesky分解算法計算信號的相關熵，然后再計算相關熵的雙譜，根據相關熵的雙譜特征識別齒輪故障，并利用仿真信號和齒輪故障實驗信號驗證了該方法的有效性和可靠性。

1 基礎理論

1.1 相關熵

2006年，美國佛羅里達大學Principe教授研究團隊，在綜合利用再生核和信息理論學習（IDL）方法的基礎上，首次提出了相關熵（Correntropy）的概念[17]。

對于任意兩個隨機變量，它們的互相關熵（廣義相關函數）可定義為

式（4）是相關熵的漸進無偏估計，因為由式（3）表示的高斯核函數是正定的Mercer核函數，因此由式（4）表示的相關熵是一個正定的對稱函數。

若直接利用式（4）計算相關熵，需要先計算核矩陣（以下簡寫為核矩陣），核矩陣是一個的半正定對稱矩陣，當較大時，計算核矩陣不僅計算效率低，而且占用計算機內存很大。因此，本文利用不完全Cholesky分解（Incomplete Cholesky Decomposition， ICD）算法計算信號的相關熵。

1.2 不完全Cholesky分解

根據矩陣Cholesky分解理論，任何的正定對稱矩陣，均可表示為

式中 是一個的下三角矩陣。

在實際數據處理中，當核矩陣的特征值下降很快時，則可以用一個（）的下三角矩陣逼近，即

式中 是一個任意小的整數，是合適的矩陣范數。

式（6）稱為矩陣的不完全Cholesky分解。當時，將大大減小計算量。在實際應用時，可以不必求出核矩陣的所有元素，再利用式（6）計算，而是采用貪婪算法逐步計算，具體算法可參考文獻[20]，其空間復雜性為，時間復雜性為，因此，當時，利用不完全Cholesky分解計算相關熵，將大大提高計算速度，降低計算機內存占用量。

1.3 基于歸一化能量的矩陣降維

在下三角矩陣中，的各列向量按矩陣的特征值大小降序排列。為進一步降低數據的復雜性，剔除噪聲影響，突出齒輪故障特征，本文通過歸一化能量方法進一步剔除冗余的列向量。下三角矩陣每一列向量的歸一化能量可表示為

設置閾值為，在下三角矩陣中刪除的列，這樣下三角矩陣的列數將縮減為，進一步降低了數據冗余度，壓縮了數據量，突出了齒輪故障特征。

1.4 雙譜估計

假設是零均值的平穩隨機過程，其三階累積量可表示為

從式（9）可以看出雙譜是變量和的函數。

根據雙譜的性質，若平穩隨機過程和統計獨立，則隨機過程+的雙譜為+。因此，使用雙譜分析可以有效抑制齒輪故障振動信號中的高斯噪聲，有效突出齒輪轉頻及其諧波、齒輪嚙合頻率及其諧波等非高斯成分。

雙譜估計有直接法和間接法兩種，本文采用直接法計算信號的雙譜[8]。

2 基于相關熵和雙譜分析的齒輪故障診斷步驟

①根據式（2）和式（6）計算信號核矩陣的不完全Cholesky分解，求出下三角矩陣;

②根據式（7）將下三角矩陣的列數縮減為;

③根據式（5）計算核矩陣;

④根據式（4）計算信號相關熵;

⑤根據式（8）和（9）計算相關熵的雙譜;

⑥根據雙譜的頻譜結構識別齒輪故障。

3 仿真驗證

齒面點蝕、剝落和裂紋是齒輪中的典型故障，伴隨著這些故障的產生，齒輪箱的嚙合振動也隨之發生變化，故障齒輪的轉頻對嚙合振動的調制作用也會逐步加強，導致調制邊頻帶的數量增加和形狀的改變，因此，齒輪故障診斷通常以齒輪某階嚙合頻率附近的窄帶信號為研究對象，根據齒輪調制邊頻帶的變化情況，識別齒輪的健康狀態。其振動信號模型可表示為[1]

式中 為齒輪的第m階嚙合頻率;為第階嚙合頻率諧波分量的初相位;為第階嚙合頻率諧波分量的幅值調制函數

式中 為幅值調制指數，即幅值調制函數的第階分量的幅值;為幅值調制函數的第階分量的初相位;為齒輪軸的轉動頻率。為第階嚙合頻率諧波分量的相位調制函數，且

式中 為調制指數，即相位調制函數的第階分量的幅值;為相位調制函數的第階分量的初相位。

根據以上分析可知，故障齒輪的激勵信號往往表現為齒輪回轉頻率對嚙合頻率及其倍頻的調制，在譜圖上形成以嚙合頻率為中心、等間隔分布的邊頻帶。一般情況下，齒輪箱中發生故障齒輪的軸頻在調制成分中所占的比例較大。

某階嚙合頻率附近的窄帶信號為單一調制頻率、調幅和調頻共存的復雜調制信號，為驗證上述分析，依據式（10）模擬齒輪嚙合頻率附近的窄帶信號，假設只含有齒輪第1階嚙合頻率，調制頻率為軸頻及其2，3倍頻。將式（10）簡化為

式中 為零均值高斯噪聲;為脈沖噪聲。取 Hz， Hz，信號采樣點數，信號采樣頻率 Hz，通過該齒輪仿真信號，驗證提出方法的有效性。

圖1（a）和圖1（b）分別為仿真信號的時域波形和FFT，可以清晰看到信號在頻域內圍繞齒輪嚙合頻率形成邊頻帶簇，邊頻帶的間隔為齒輪軸的轉頻。

圖2為仿真信號相關熵（）的雙譜，從圖2中的雙頻平面內可以清晰看到在，以及等6條直線的交點處，圍繞齒輪嚙合頻率形成邊頻帶簇，邊頻帶的間隔為齒輪軸的轉頻。為了能清晰識別邊頻帶簇，圖3給出了在附近的局部放大圖，從圖3可以看出：以為中心，分布著齒輪軸的1階、2階邊頻帶，這種頻譜特征表明了齒輪的故障特征，與理論分析一致。

在仿真信號中加入零均值高斯噪聲，信噪比為 dB，之后再隨機加入幾個幅值不同的脈沖信號，以模擬非高斯脈沖噪聲，圖4（a）和圖4（b）分別為仿真信號的時域波形和FFT，由于仿真信號完全被強噪聲淹沒，因此從圖4（a）已完全看不出信號幅值的變化規律，從圖4（b）也不能識別齒輪的嚙合頻率及其邊頻帶。

根據第2節介紹的步驟，計算仿真信號的相關熵（）及其雙譜。仿真信號的相關熵如圖5所示，從圖5可以看出相關熵的時域波形呈現出幅值調制的特征，圖4（a）中幅值較大的脈沖噪聲已被完全抑制，相關熵只保留了信號中的周期成分。仿真信號相關熵的雙譜如圖6和圖7所示，從圖6和7可以看出，在強高斯噪聲和非高斯噪聲的影響下，基于相關熵的雙譜仍然能夠識別齒輪的故障特征，圖2中的點狀邊頻帶譜峰變成圖6中的直線分布，，以及等6條頻譜線兩側的邊頻帶呈直線分布，清晰可見，在這6條頻譜線兩側圍繞齒輪嚙合頻率形成邊頻帶簇譜線，邊頻帶譜線的間隔為齒輪軸的轉頻。圖8給出了在附近的局部放大圖，從圖8可以清晰看出：以為中心，分布著齒輪軸的1階、2階邊頻帶，由此可見，盡管在強噪聲干擾下，基于相關熵的雙譜仍然能準確提取齒輪的故障特征。

為凸顯相關熵的降噪能力，將相關熵雙譜與傳統雙譜和基于小波閾值降噪雙譜[6]進行對比。圖9和10給出了利用直接法計算的仿真信號的雙譜，圖11和12為采用小波閾值降噪后信號的雙譜，從圖9?10和圖11?12可以看出，仿真信號的雙譜和小波閾值降噪后雙譜已完全被強噪聲淹沒，完全不能分辨齒輪的嚙合頻率及其邊頻帶簇。對比圖7和圖10，12，圖7中相關熵的雙譜噪聲方差較小，而圖10，12中噪聲方差依然很大。可見盡管雙譜對高斯噪聲具有一定的抑制能力，但當信號中含有很強的高斯噪聲和非高斯噪聲時，雙譜也難以有效提取齒輪的故障特征。而小波閾值降噪方法在處理強噪聲干擾時，也難以取得理想的效果。

通過上述仿真信號可知：由于相關熵能有效抑制高斯噪聲和非高斯脈沖噪聲，因此基于相關熵的雙譜分析具有從強高斯噪聲和非高斯噪聲背景中提取齒輪故障特征的能力，基于相關熵的雙譜分析為高斯、非高斯噪聲的處理提供了一種嶄新的魯棒性解決方法。

4 齒輪故障診斷

齒輪箱振動信號采集系統可參考文獻[21]，齒輪箱輸入軸齒輪齒數=28，輸出軸齒輪齒數為，用人工方法將輸出軸齒輪上某一齒的嚙合線附近磨掉約0.4 mm，以模擬齒輪單齒磨損故障。實驗時采樣點數為2048，采樣頻率為16384 Hz，電機轉速為1473 r/min，因此輸入軸回轉頻率 Hz，輸出軸回轉頻率為 Hz， 齒輪1階嚙合頻率為 Hz。

圖13為齒輪箱輸出軸齒輪單個齒面磨損時齒輪箱箱體振動信號的時域圖及其FFT，從頻譜圖中能清晰看到齒輪1階、2階和3階嚙合頻率，但嚙合頻率兩側邊頻帶信息模糊。在圖13（b）中，齒輪的2階嚙合頻率呈現出最大的譜峰，表明齒輪箱2階嚙合頻率具有最大的振動能量。

為了驗證基于相關熵的雙譜分析在齒輪故障診斷中的有效性，根據本文提出的方法，計算齒輪磨損故障信號的相關熵的雙譜。圖14為根據式（6）計算信號核矩陣的不完全Cholesky分解求出的下三角矩陣各列的歸一化能量，矩陣的列數為82，從圖14可以看出，有些列向量的能量很小。因此，根據式（7）將下三角矩陣的列數縮減為32，由于降低了數據冗余度，壓縮了數據量，不僅提高了相關熵計算的速度，而且降低了噪聲影響，突出了齒輪故障特征。

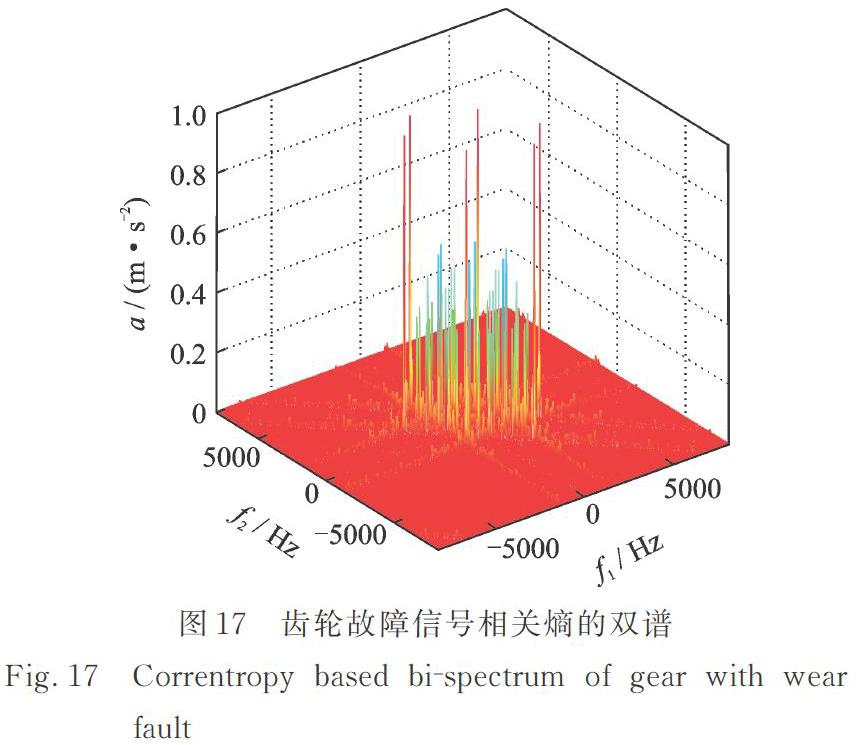
圖15為齒輪故障振動信號的相關熵，從圖15可以看出相關熵的時域波形呈現出明顯的調制特征，說明相關熵能有效提取信號中的周期成分。圖16和17為齒輪故障振動信號相關熵的雙譜，從圖16和17可以看出，雙譜圖中的譜峰呈離散點狀分布，幾乎沒有受到噪聲的影響，基于相關熵的雙譜能夠準確顯示齒輪的故障特征，以及等10條直線的交點處，圍繞齒輪嚙合頻率及其倍頻形成邊頻帶簇，邊頻帶的間隔為齒輪軸的轉頻。尤其在，和等位置附近具有顯著的邊頻帶譜峰，這種頻譜特征表明了齒輪的故障特征，同時也說明齒輪箱的2階嚙合頻率具有最大的振動能量，與圖13（b）FFT頻譜圖的計算結果一致。

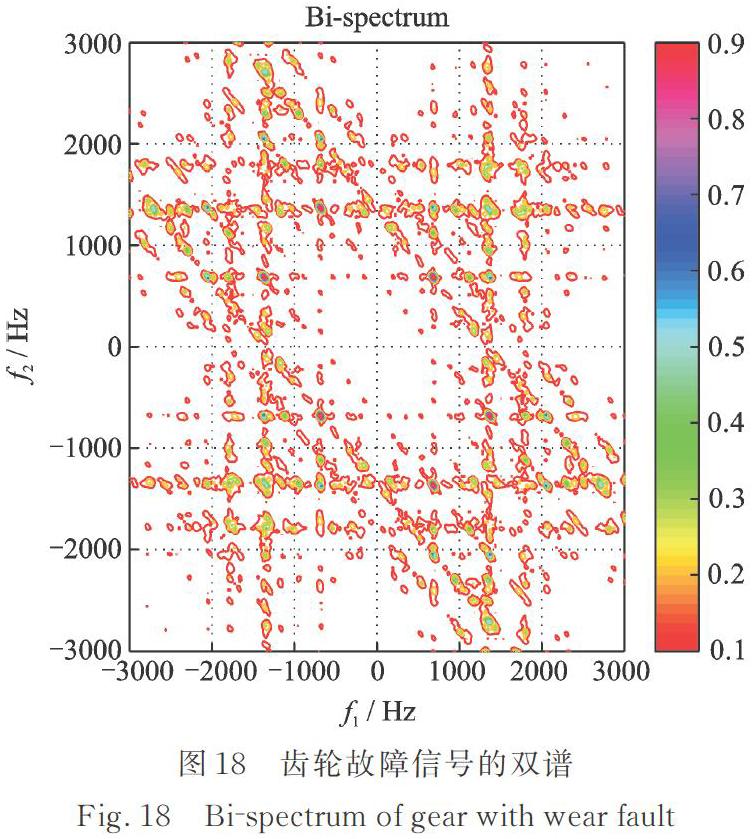
為了進行對比，驗證本文提出方法的有效性，圖18和19給出了利用直接法計算的齒輪故障振動信號的雙譜，圖20和21為采用小波閾值降噪后信號的雙譜[6]。從圖18?19和圖20?21可以看出，在和等位置出現顯著的譜峰，表明齒輪1階嚙合頻率和2階嚙合頻率具有很強的非線性耦合，但齒輪故障振動信號的雙譜和小波閾值降噪后的雙譜已完全被強噪聲淹沒，難以準確分辨齒輪嚙合頻率附近的邊頻帶，因而不能準確提取齒輪的故障特征。

通過上述分析可以看出：相關熵具有抑制高斯噪聲和非高斯噪聲的能力，能有效提取齒輪故障信號中的周期沖擊成分;基于相關熵的雙譜綜合利用了相關熵和雙譜的優點，能有效處理非線性、非高斯信號，具有很強的從強噪聲背景中提取齒輪故障特征的能力，因而基于相關熵的雙譜技術能有效提取齒輪故障的邊頻帶，能在雙頻平面內很清晰地刻畫齒輪的故障特征，提高了齒輪故障診斷的可靠性和準確性，為從強噪聲環境中提取齒輪故障特征的有效方法。

5 結 論

雙譜具有很強的消噪能力，理論上可以抑制高斯噪聲，但卻不能有效抑制非高斯噪聲的干擾。相關熵不僅能有效抑制高斯噪聲，而且能有效抑制非高斯噪聲，因此，相關熵為高斯、非高斯噪聲的處理提供了一種嶄新的魯棒性解決方法。綜合利用了相關熵和雙譜的優點，提出了基于相關熵雙譜分析的齒輪故障診斷方法，并利用ICD對核矩陣進行降維，壓縮了數據量，突出了齒輪故障特征，提高了計算速度。仿真和齒輪磨損故障實驗結果表明：基于相關熵的雙譜分析技術，能有效提取淹沒在強噪聲環境中的微弱信號，提高了信噪比，為一種齒輪故障診斷的有效方法。

參考文獻：

[1] 丁 康，李巍華，朱小勇.齒輪及齒輪箱故障診斷實用技術[M].北京：機械工業出版社，2005：1-4.

Ding Kang， Li Weihua， Zhu Xiaoyong. Practical Technology of Gear and Gear Box Fault Diagnosis[M].Beijing： China Machine Press， 2005： 1-4.

[2] 楊江天，陳家驥，曾子平. 雙譜分析及其在機械診斷中的應用[J]. 中國機械工程， 2000， 11（4）： 424-426.

Yang Jiangtian， Chen Jiaji， Zeng Ziping. Bispectral analysis and its application in machinery diagnosis[J]. China Mechanical Engineering， 2000， 11（4）： 424-426.

[3] Bouillaut L， Sidahmed M. Cyclostationary approach and bilinear approach： Comparison， applications to early diagnosis for helicopter gearbox and classification method based on HOCS[J]. Mechanical Systems & Signal Processing， 2001， 15（5）： 923-943.

[4] Antoniadis I， Glossiotis G. Cyclostationary analysis of rolling-element bearing vibration signals[J]. Journal of Sound and Vibration， 2001， 248（5）： 829-845.

[5] 熊良才，史鐵林，楊叔子.基于雙譜分析的齒輪故障診斷研究[J].華中科技大學學報，1999，27（3）：6-8.

Xiong Liangcai， Shi Tielin， Yang Shuzi. A method for extracting mechanical faults features based on higher-order statistics[J]. Journal of Huazhong University of Science and & Technology， 1999， 27（3）： 6-8.

[6] 李軍偉，韓 捷，李志農， 等.小波變換域雙譜分析及其在滾動軸承故障診斷中的應用[J].振動與沖擊，2006，25（5）：92-95.

Li Junwei， Han Jie， Li Zhinong， et al. Bispectrum analysis in the wavelet transform domain and its application to the fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock， 2006， 25（5）： 92-95.

[7] 唐貴基，王曉龍. 基于局部均值分解和切片雙譜的滾動軸承故障診斷研究[J].振動與沖擊，2013， 32（24）： 83-88.

Tang Guiji， Wang Xiaolong. Fault diagnosis of roller bearings based on local mean decomposition and slice bispectrum [J]. Journal of Vibration and Shock， 2013， 32（24）： 83-88.

[8] 李 輝，鄭海起，唐力偉.基于倒雙譜分析的軸承故障診斷研究[J].振動、測試與診斷，2010，30（4）： 353-356.

Li Hui， Zheng Haiqi， Tang Liwei. Application of bi-cepstrum technique to bearing fault detection[J]. Journal of Vibration Measurement & Diagnosis， 2010， 30（4）： 353-356.

[9] Raad A， Sidahmed M. Gear fault diagnosis using cyclic bispectrum[J]. IFAC Proceedings Volumes， 2002， 35（1）： 431-436.

[10] 朱忠奎，孔凡讓，王建平，等.循環雙譜及其在齒輪箱故障識別中的應用研究[J].振動工程學報，2004， 17（2）：224–227.

Zhu Zhongkui， Kong Fanrang， Wang Jianping， et al. Study on the applications of cyclic bispectrum in gearbox fault diagnosis[J]. Journal of Vibration Engineering， 2004， 17（2）： 224-227.

[11] 周 宇，陳 進，董廣明，等.基于循環雙譜的滾動軸承故障診斷[J].振動與沖擊， 2012， 31（9）： 78-81.

Zhou Yu， Chen Jin， Dong Guangming， et al. Fault diagnosis of rolling element bearing based on cyclic bispectrum[J]. Journal of Vibration and Shock， 2012， 31（9）： 78-81.

[12] 陳 進，姜 鳴. 高階循環統計量理論在機械故障診斷中的應用[J]. 振動工程學報， 2001， 14（2）： 125-134.

Chen Jin， Jiang Ming. The state-of-art of the application of the higher-order cyclostationary statistics in mechanical fault diagnosis[J]. Journal of Vibration Engineering， 2001， 14（2）： 125-134.

[13] 鄭海波，陳心昭，李志遠.基于雙譜的齒輪故障特征提取與識別[J].振動工程學報，2002，15（3）： 354-358.

Zheng Haibo， Chen Xinzhao， Li Zhiyuan. Bispectrum based gear fault feature extraction and diagnosis[J]. Journal of Vibration Engineering， 2002， 15（3）： 354-358.

[14] 周雁冰，柳亦兵，李 宏，等.基于雙譜熵的齒輪裂紋故障特征提取[J]. 中國機械工程， 2013，24（2）： 190-194.

Zhou Yanbing， Liu Yibing， Li Hong， et al. Fault feature extraction for gear crack based on bispectral entropy[J]. China Mechanical Engineering， 2013， 24（2）： 190-194.

[15] 程軍圣，李海龍，楊 宇. 基于BLCD和雙譜的齒輪故障診斷方法[J].振動與沖擊， 2013， 32（8）： 31-34.

Cheng Junsheng， Li Hailong， Yang Yu. A gear fault diagnosis method based on BLCD and wavelet domain bispectrum[J]. Journal of Vibration and Shock， 2013， 32（8）： 31-34.

[16] 李學軍，蔣玲莉，楊大煉， 等.基于雙譜分布區域的齒輪聚類分析與故障診斷[J].振動工程學報， 2011，24（3）： 304-308.

Li Xuejun， Jiang Lingli， Yang Dalian， et al. Cluster analysis and fault diagnosis for gear based on bispectrum distribution[J]. Journal of Vibration Engineering， 2011，24（3）： 304-308.

[17] Santamaria I， Pokharel P P， Principe J C. Generalized correlation function： Definition， properties， and application to blind equalization[J]. IEEE Transactions on Signal Processing， 2006， 54（6）： 2187-2197.

[18] Liu W， Pokharel P P， Principe J C. Correntropy： Properties and applications in non-Gaussian signal processing [J]. IEEE Transactions on Signal Processing， 2007， 55（11）： 5286-5298.

[19] Gunduz A， Principe J C. Correntropy as a novel measure for nonlinearity tests[J]. Signal Processing， 2009， 89（1）： 14-23.

[20] Bach F R， Jordan M I. Predictive low rank decomposition for kernel methods[C]. Machine Learning， Proceedings of the Twenty-Second International Conference （ICML 2005）， Bonn， Germany， August 7-11， 2005.

[21] Li Hui， Zhang Yuping， Zheng Haiqi. Wear detection in gear system using Hilbert-Huang transform[J]. Journal of Mechanical Science and Technology， 2006， 20（11）： 1781-1789.

作者簡介： 李 輝（1968-），男，博士，教授。電話： 15931170851; E-mail： huili68@163.com