Fermat型偏微差分方程解的存在性及形式

汪 楠，徐洪焱，劉 林

(1.江西醫(yī)學(xué)高等專(zhuān)科學(xué)校醫(yī)學(xué)影像系，江西 上饒 334001;2.上饒師范學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，江西 上饒 334001)

1 引言及主要結(jié)果

文章假定讀者熟悉Nevanlinna值分布理論，我們將采用Nevanlinna理論的基本符號(hào)[1-3]。隨著Nevanlinna理論在差分領(lǐng)域的快速發(fā)展，許多學(xué)者在差分方程等方面獲得了一系列重要且有趣的結(jié)果(見(jiàn)文獻(xiàn)[4-9])。2012年間，劉凱，楊連中等[7-9]討論了幾類(lèi)Fermat型復(fù)域微分、差分方程

f′(z)2+f(z+c)2=1

(1.1)

f(z)2+f(z+c)2=1

(1.2)

f(z)2+f′(z)2=1

(1.3)

其中c∈為非零常數(shù)，他們得到:方程(1.1)的有限級(jí)超越整函數(shù)解必為f(z)=sin(z±Bi)，其中c=2kπ或c=(2k+1)π，B∈，k∈N；方程(1.2)的有限級(jí)超越整函數(shù)解必為f(z)=sin(Az+B)，其中，k∈N；方程(1.3)的有限級(jí)超越整函數(shù)解為f(z)=sin(z+c)，c∈。

2018年，Xu-Cao[10-11]利用多復(fù)變Nevanlinna值分布理論以及差分模擬結(jié)果，討論了多變量Fermat型偏微-差分方程解的性質(zhì)，將劉凱等人的結(jié)果推廣到多變量情形。

定理A[10-11]設(shè)c=(c1，c2)∈2，則偏微差分方程

的任意有限級(jí)超越整函數(shù)解具有形式f(z1，z2)=sin(A1z1+A2z2+B)，其中A1，A2，B為常數(shù)，滿(mǎn)足A1eiA1c1=1，特別地，若c1=0，則f(z1，z2)=sin(z1+A2z2+B)。

定理B[10]設(shè)c∈n{0}。那么Fermat型偏微差分方程

f(z)2+f(z+c)2=1

(1.4)

的解具有

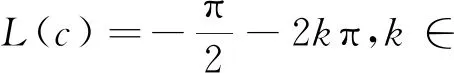
由于涉及多變量差分Nevanlinna理論[12-13]起步較晚，有關(guān)復(fù)域偏微分與差分方程的文獻(xiàn)并不多，關(guān)于Fermat型偏微差分方程的還有許多問(wèn)題有待研究。本文將針對(duì)此問(wèn)題，進(jìn)一步討論Fermat型偏微差分方程解的存在性條件及其形式，獲得結(jié)果如下：

定理1.1設(shè)c=(c1，c2)∈2-{(0，0)}，若f(z1，z2)為方程

(1.5)

的有限級(jí)超越整函數(shù)解，則f(z1，z2)具有形如

這里L(fēng)(z)=μ1z1+μ2z2;a1，a2≠0且L(c)=μ1c1+μ2c2，μ1，μ2，b∈滿(mǎn)足以下情況之一:

以下例子顯示方程(1.5)解的存在性。

例1.1若

則f(z1，z2)為方程(1.5)的有限級(jí)超越整函數(shù)解，其中μ1=0，μ2=2，b∈，。

例1.2若

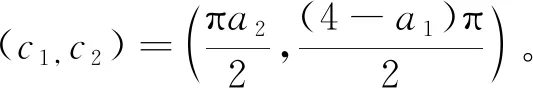
則易知f(z1，z2)為方程(1.5)的有限級(jí)超越整函數(shù)解。

若方程(1.5)同時(shí)包含兩類(lèi)偏微分以及差分，那么

定理1.2設(shè)c=(c1，c2)∈2{(0，0)}，s=c2z1-c1z2。若f(z1，z2)為方程

(1.6)

的有限級(jí)超越整函數(shù)解，則f(z1，z2)具有

這里a1≠0，a2，a3不同時(shí)為零，L(z)=μ1z1+μ2z2，H(s)是關(guān)于s的多項(xiàng)式且L(c)=μ1c1+μ2c2，μ1，μ2，b∈滿(mǎn)足以下情況之一:

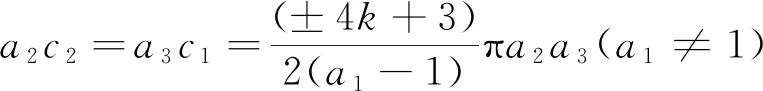
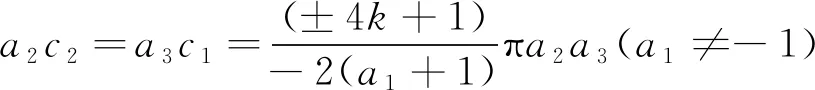
(ⅱ) 若a2c2≠a3c1，則H(s)≡0且

或

下列例子說(shuō)明方程(1.6)解的存在性與形式的準(zhǔn)確性。

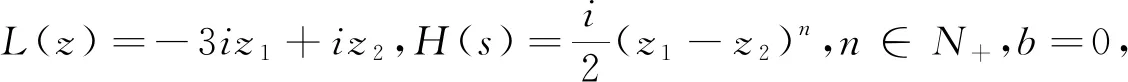
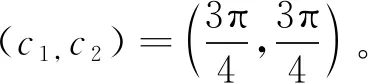
例1.7令L(z)=iz1-iz2，H(s)≡0，b=0，則

例1.8令L(z)=-iz1-iz2，H(s)≡0，b=0，a1=1，a2=a3=1，則

2 引理

文章須用到以下引理。

引理2.1[14-15]若F為n上的整函數(shù)，F(xiàn)(0)≠0，ρ(nF)=ρ<∞，則存在函數(shù)fF與gF∈n，滿(mǎn)足F(z)=fF(z)egF(z)，特別地，當(dāng)n=1時(shí)，fF是魏爾斯特拉斯函數(shù)。

注2.1這里ρ(nF)是零點(diǎn)計(jì)數(shù)F的階數(shù)。

引理2.2[3]若g與h是復(fù)平面的整函數(shù)，且g(h)是有限級(jí)整函數(shù)，則存在以下兩種情況：

(ⅰ)h為多項(xiàng)式，g為有限級(jí)整函數(shù)；

(ⅱ)h為非多項(xiàng)式的有限級(jí)整函數(shù)，g為零級(jí)超越整函數(shù)。

引理2.3[16]設(shè)fj(≠0)，j=1，2，3是m上的亞純函數(shù)，f1非常數(shù)。如果f1+f2+f3=1以及

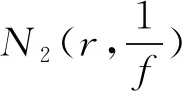
3 定理1.1的證明

設(shè)f(z)為方程(1.5)的有限級(jí)超越整函數(shù)解，重寫(xiě)方程(1.5)為

(3.1)

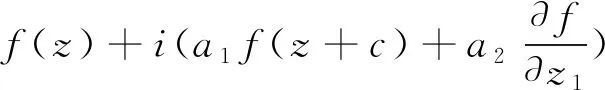
于是

(3.2)

(3.3)

將(3.2)代入(3.3)，得

(3.4)

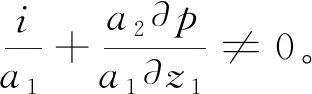
(3.5)

由(3.4)，(3.5)，得

(3.6)

根據(jù)(3.5)，(3.6)，可知e2[p(z+c)-p(z)]=-1，可得

p(z)=L(z)+H(s)+b，e2L(c)=-1

這里L(fēng)是一個(gè)線(xiàn)性函數(shù)，形如L(z)=μ1z1+μ2z2，H(s)是關(guān)于s的多項(xiàng)式，其中s=c2z1-c1z2，μ1，μ2，b∈。

另一方面，由(3.5)，(3.6)知

即

由(3.5)或(3.6)，知

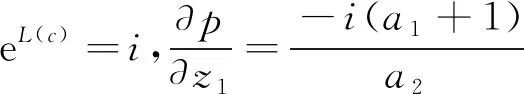
那么

如果c2=0，即H(s)=H(-c1z2)，又因?yàn)閑2[p(z+c)-p(z)]=-1，則degsH≤1。

如果c2≠0，易知H(s)是關(guān)于s的多項(xiàng)式且degsH≤1。因此，L(z)+H(s)+b是關(guān)于z1，z2的線(xiàn)性，不妨設(shè)μ1z1+μ2z2+b，μ1，μ2，b∈。結(jié)合(3.5)與(3.6)，則

這里L(fēng)(z)=μ1z1+μ2z2，且L(c)，μ1，μ2，b∈滿(mǎn)足

于是，定理1.1得證。

4 定理1.2的證明

假設(shè)f(z)是方程(1.6)的解，類(lèi)似上述證明，存在非常數(shù)多項(xiàng)式p(z)，使得

(4.1)

(4.2)

由(4.1)與(4.2)得

e2[p(z+c)-p(z)]=-1

于是p(z)=L(z)+H(s)+b，這里L(fēng)是線(xiàn)性函數(shù)，形如L(z)=μ1z1+μ2z2，H(s)是關(guān)于s的多項(xiàng)式，其中s=c2z1-c1z2，μ1，μ2，b∈，且e2L(c)=-1。

另一方面，由(4.1)，(4.2)得

再根據(jù)上述所知p(z)=L(z)+H(s)+b，有

(4.3)

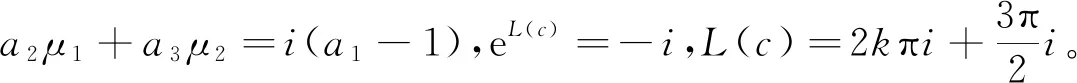
若a1=1，a2μ1+a3μ2=0，則L(c)=0，eL(c)=1，這與上述e2L(c)=-1矛盾。

這里k∈Z。

若a1=-1，a2μ1+a3μ2=0，則L(c)=0，eL(c)=1，這與上述e2L(c)=-1矛盾。

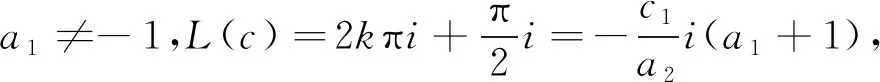
或

綜上，定理1.2證畢。