Winkler地基上矩形薄板的振動響應分析

鄭雙星，高芳清,2，丁凱文

（1.西南交通大學 力學與工程學院，成都 610031；2.西南交通大學 應用力學與結構安全四川省重點實驗室，成都 610031）

分析彈性地基上矩形薄板振動響應問題可以采用能量變分法[1-2]、有限元法[3-6]、樣條元法[7-10]。另外，顏可珍[11]通過級數展開法和Laplace-Fourier 變換方法得到了薄板在半波正弦沖擊荷載作用下位移和應力的解析解。袁松等[12]運用接觸力學的理論對Winkler地基模型落石沖擊力計算方法進行了研究。吳波[13]用曲厚板單元分析法對彈性地基上不規則厚板的簡載應力進行了求解。

對于地基上板類結構常采用Winkler地基建模，該模型形式簡單、參數設定簡潔，為工程界普遍接受而得到廣泛應用。本文通過Winkler 地基模型反映地基-薄板結構相互作用關系，通過彈性組件的設定來模擬矩形薄板邊界約束類別[14]，采用Li 等[15-16]提出的改進的傅里葉級數方法來表示橫向位移，通過數值計算，求得Winkler地基上矩形薄板的振動響應曲線，并通過和有限元結果進行對比，表明本文方法精度較高。此外，該方法收斂速度也比較快。

1 理論模型

1.1 改進傅里葉級數解

對于彈性約束邊界條件下單一矩形板結構來說，其橫向位移函數可以采用二維改進傅里葉級數形式表示，即在標準二維傅里葉余弦級數基礎上增加輔助函數與單傅里葉余弦級數的乘積[17-18]；通過輔助函數的引入，可以解決傳統的傅里葉級數的導數在邊界處潛在的不連續性問題，同時還可以改善級數的收斂性。

橫向位移函數用二維改進傅里葉級形式表示為

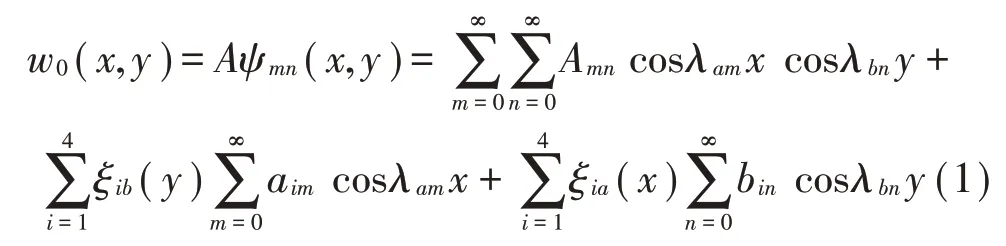
式中：A和aim、bin分別為橫向位移函數w0(x,y)中二維傅里葉級數和輔助級數的未知系數向量，λam=mπ/a，λbn=nπ/b，向量A、ψmn(x,y)的形式以及x相關的輔助函數ξia(x)可表示為：

將式(4)至式(7)中a和x分別替換為b和y即可得到輔助函數ξib(y)的表達式。

1.2 計算模型建立

計算模型如圖1所示。基于Winkler地基模型，在垂直于x-y平面方向采用均勻分布的豎向彈簧模擬地基作用，該豎向彈簧相互獨立且互不影響；采用系列橫向彈簧和扭轉彈簧組件來模擬矩形薄板邊界(kx0、kxa和Kx0、Kxa分別為x=0和x=a邊界上的橫向彈簧剛度和扭轉彈簧剛度，ky0、kyb和Ky0、Kyb分別為y=0和y=b邊界上的橫向彈簧剛度和扭轉彈簧剛度)；f(x，y，t)為施加于薄板上（x0，y0）位置處的簡諧橫向集中力。

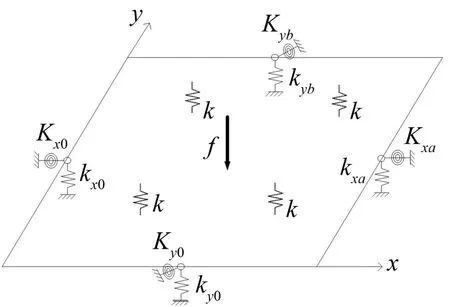
圖1 受簡諧橫向集中力作用Winkler地基上矩形薄板模型

具有彈性邊約束和結構阻尼的板振動控制微分方程式為：

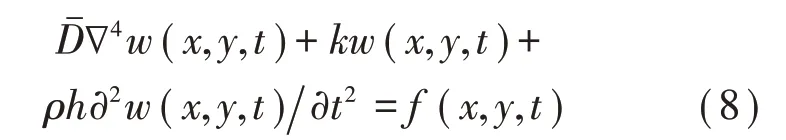
簡諧橫向集中力（幅值為）可表示為：

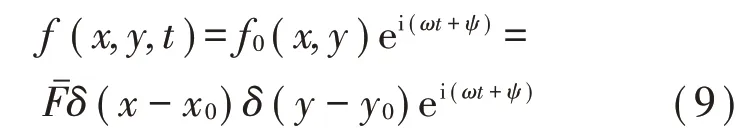
此時，橫向位移可以寫為：

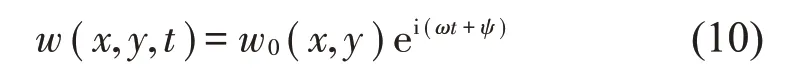
將式（9）、式（10）代入式（8），可以得到：

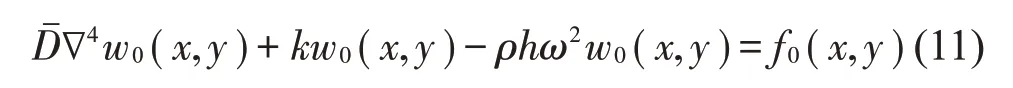
本文采用能量法求解振動方程式（11）。

在外部荷載作用下Winkler 地基上矩形板結構拉格朗日函數表示為：

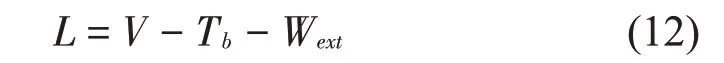
式中：V為Winkler地基上矩形薄板的總勢能，Tb為該結構的總動能，Wext為外力的勢能的負值。

系統中存儲的總勢能V可表示為：

式中：Vf為Winkler 地基的變形勢能，Vb為彎曲應變能，Vs為邊界彈簧的彈性勢能，其具體表達式可以參見文獻[19]。

Wex可以表示為：

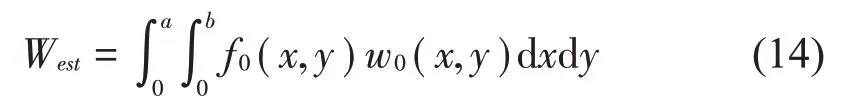
將式(1)代入拉格朗日函數式(11)中，然后用瑞利-里茲方法對該拉格朗日函數求極值，可以得到一個線性方程組，將其用矩陣表達式表示為：

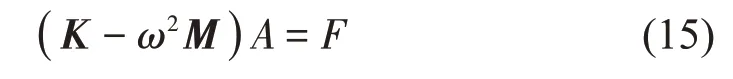
式中：K、M分別為Winkler 地基上矩形薄板系統的剛度矩陣和質量矩陣，其取值只與系統的結構特征地基參數和邊界條件有關。

F為橫向集中力作用向量，即：

任意激勵頻率ω下矩形板結構振動響應的傅里葉系數向量A可由式（15）直接得到：

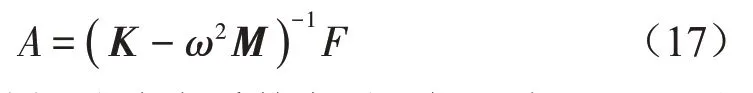
將求得的振動響應系數向量A代入式（1），再通過式（10）即可得到該激勵下矩形薄板結構在任意時刻的橫向位移。

對于簡諧振動，在計算出結構振動位移響應之后，結構振動速度可以由v=jωw直接獲得，根據得到結果的實部與虛部，即可求得速度的幅值與相位。

向量F取為零向量，即可進行模態分析，求得固有頻率。

2 數值計算與分析

給定如下參數：板長a=1.0 m，寬b=1.0 m，厚h=0.008 m，密度ρ=7 800 kg/m3，彈性模量E=2×1011N/m2，泊松比μ=0.3，地基基床系數k=5.5×107N/m3，阻尼系數η=0.02。為表述簡潔，下文中用F表示自由邊界條件（橫向彈簧剛度設置為0，扭轉彈簧剛度系數設置為0），S表示簡支邊界條件（橫向彈簧剛度設置為1010N/m，扭轉彈簧剛度系數設置為0），C表示固支邊界條件（橫向彈簧剛度設置為1010N/m，扭轉彈簧剛度系數設置為1010N?m/rad）。ANSYS 有限元模型中采用shell63 單元，網格劃分尺寸為0.01 m×0.01 m。

表1 給出了截斷值M、N取值為6 時Winkler 地基上不同邊界條件下矩形薄板前6階固有頻率與有限元結果對比。從表中可以看出，無論取何種邊界條件，兩種方法所求出的固有頻率都非常接近。

表1 Winkler地基上不同邊界矩形薄板的固有頻率/Hz

在以下分析中，所有邊界條件均取為簡支。

表2給出了四邊簡支條件下基于本文方法及有限元法所得500 Hz以下的固有頻率。

表2 Winkler地基上四邊簡支矩形薄板的固有頻率/Hz

將幅值為1 N的簡諧橫向集中力施加于板中心位置（0.5 m，0.5 m），并在0～500 Hz 頻率范圍內進行正弦掃描，同時對該作用點和（0.8 m，0.8 m）位置處的振動速度幅值進行觀測。此外，為了驗證本文方法的可靠性，采用ANSYS有限元方法對相同問題進行了計算，并與程序計算結果進行對比，如圖2所示。

將幅值為1 N 的簡諧橫向集中力施加于板（0.8 m，0.8 m）位置處，并在0～500 Hz 頻率范圍內進行正弦掃描，同時對該作用點和（0.5 m，0.5 m）位置處振動速度幅值進行觀測，將本文方法所得結果與有限元方法所得結果對比，如圖3所示。

如圖2至圖3所示，藍色實線為本文方法計算結果（Current），紅色虛線為有限元分析（Finite Element Analysis，圖中采用符號“FEA”）計算結果，可以發現，在頻率較高時兩者存在一定偏差，而在低頻帶范圍內吻合很好，驗證了本文方法能夠預測Winkler地基上板結構的響應幅值。

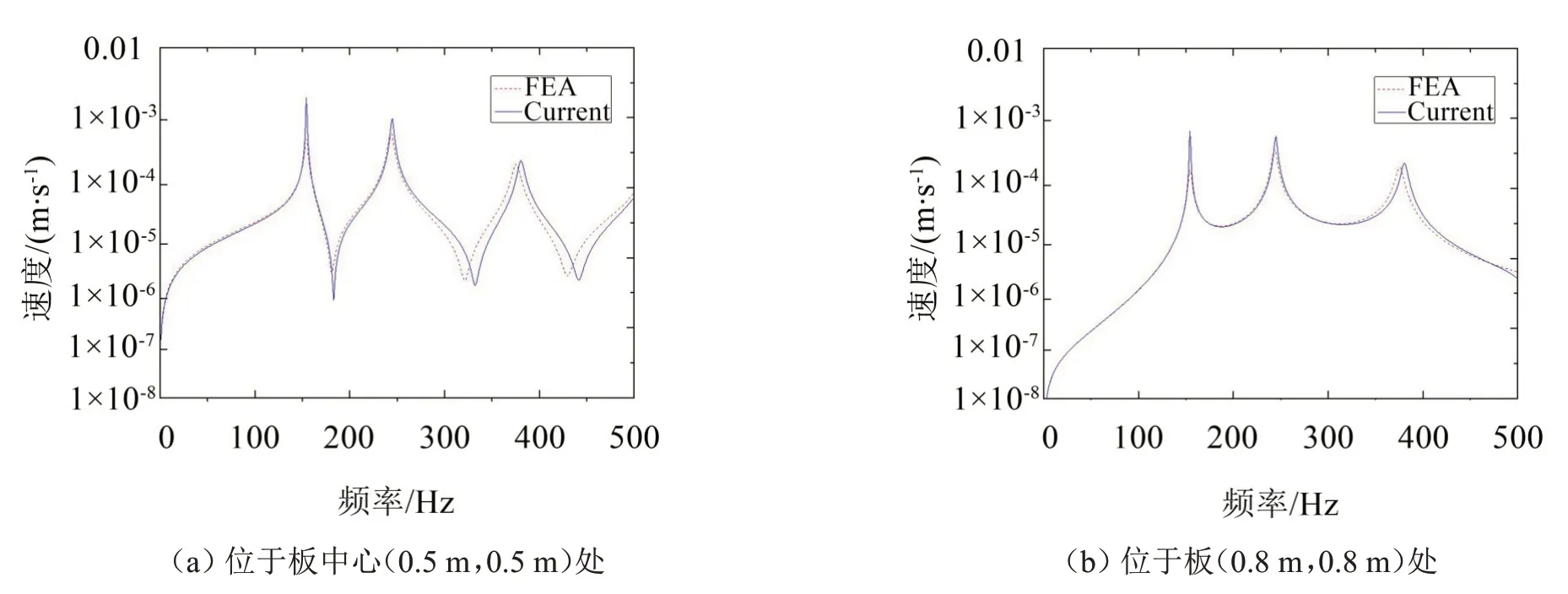
圖2 施加于板中心位置（0.5 m，0.5 m）處橫向集中力作用下不同位置振動速度的幅值

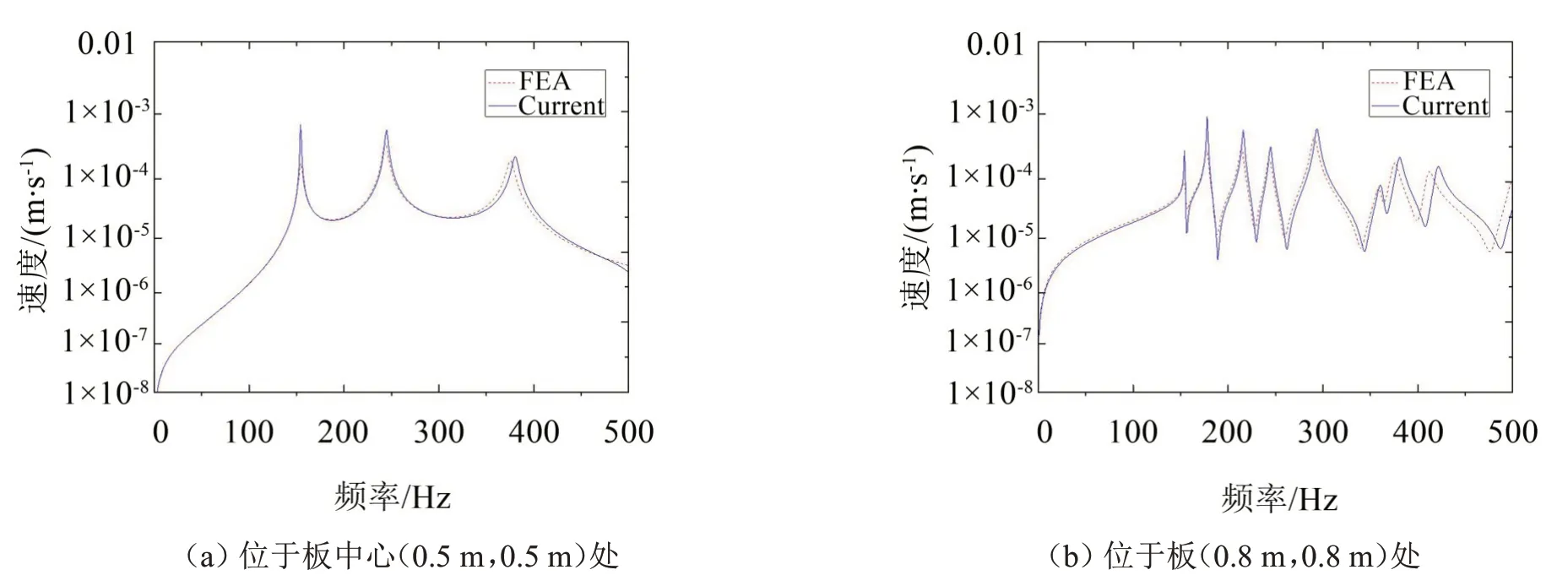
圖3 施加于板（0.8 m，0.8 m）處橫向集中力作用下不同位置振動速度的幅值

另外，對比圖2 至圖3 可以發現，在中心點處激勵時，有較少的結構模態被激起；在非中心點處激勵時，在中心點處有較少的結構模態被激起，在非中心點處有較多的結構模態被激起。出現上述特點是因為矩形薄板結構模態分布本身具有明顯對稱性，其中有些模態節線過中心點，因此在中心點處有更少的結構模態被激起。

將幅值為1 N、初相位ψ=arctan(4/3)的簡諧橫向集中力施加于板（0.8 m，0.8 m）位置處，在0～500 Hz頻率范圍內進行正弦掃描，同時對該作用點和（0.5 m，0.5 m）位置處振動速度的相位進行觀測，將本文方法所得結果與與有限元方法所得結果對比，如圖4所示。

如圖4 所示，藍色實線為本文方法計算結果（Current），紅色虛線為有限元分析計算結果，可以發現，在較高頻率和相位極值點兩者存在一定偏差，兩種結果在低頻帶范圍內吻合較好，驗證了本文方法能夠在一定程度上預測Winkler 地基上板結構響應的相位。

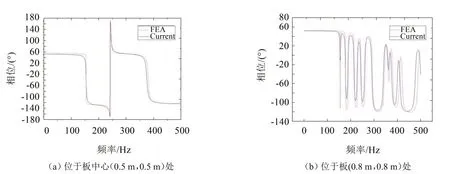
圖4 施加于板（0.8 m，0.8 m）處橫向集中力作用下不同位置振動速度的相位

3 結語

本文將改進傅里葉級數法運用到Winkler 地基上薄板的振動響應分析上，得到了響應的幅值與相位，并與有限元結果進行了對比，得到以下結論：

（1）在截斷值M=N=6 時，基于本文方法所得固有頻率結果已有較高精度，表明改進傅里葉級數法中假設的位移函數在求解域中足夠光滑，且收斂速度快；

（2）在數值算例中給出了四邊簡支彈性地基上板結構的振動響應（幅值與相位），通過與有限元方法的結果比較，驗證了本文方法的可行性和準確性；

（3）在中心點處激勵，同時在中點處求解響應，共振峰數目減少。而在非中心點激勵同時在非中心點處求解響應，會有最多的共振峰值。