基于模糊自抗擾的風電場儲能虛擬慣量控制

崔海林 ，李泰 ，潘榮睿

（1.江蘇科技大學電子信息學院，江蘇 鎮江 212003；2.江蘇大學電氣信息工程學院，江蘇 鎮江 212013；3.江蘇輝能電氣有限公司，江蘇 鎮江 212132；4.江蘇省常州技師學院，江蘇 常州 213032）

隨著新能源的發展，電力電子類設備并網增多，能夠支撐電網頻率的風電場慣性降低[1]。雙饋風力發電機通過變頻器與電網連接，使得轉速與電網頻率解耦，無法對系統頻率變化做出自動響應[2]。新的電網導則[3]要求，當頻率發生跌落時并網風電機組應當具備慣性支持功能。

虛擬慣量控制能夠在電網頻率跌落時，為電網提供慣量支持[4]。風電系統中旋轉設備和儲能（energy storage，ES）設備具有潛在慣性支持能力，文獻[5]利用轉子動能提供慣性支持，然而在風電機轉子轉速恢復時會引起電網頻率二次跌落；文獻[6]利用模糊控制的轉子轉速恢復器來進行轉子動能慣性控制，該方法難以適應變化的電網做出自適應參數控制；文獻[7]研究模糊控制器對儲能燃料電池荷電狀態的影響，然而風速的不確定性和系統的多個未知擾動，系統慣性、驅動力矩等參數變化范圍較大，難以抵抗未知參數擾動；文獻[8]利用擴張狀態觀測器來漸近估計電網頻率總擾動，然而需要整定的參數過多，影響了控制精度；文獻[9]采用主動自抗擾控制的最大功率跟蹤控制方法來補償轉子電流擾動，然而風電機組受功率擾動的同時仍受到轉子電流擾動的影響。基于此，在電網頻率波動的情況下提高系統的抗干擾能力是不可或缺的。

在最大風功率跟蹤情況下，受負荷波動和風速不確定的作用，為保證電網能實時提供電網頻率支撐，提出一種基于模糊自抗擾（fuzzy logic control auto disturbance rejection control，FLC-ADRC）的儲能慣量控制方法，針對自抗擾控制器內部參數不利于實際操作和整定，引進模糊規則，結合各自優勢，給出模糊自抗擾控制器算法，在Matlab/Simulink中進行系統建模與仿真。仿真結果證實了與采用模糊邏輯（fuzzy logic control，FLC）儲能慣量控制的方法相比，所提出的基于FLC-ADRC的儲能慣量控制方法響應速度快、魯棒性好、頻率穩定。

1 雙饋風電機組慣量控制方法

風電系統模型如圖1所示，該模型由雙饋風力發電機，轉子側、網側變流器以及電網等組成。

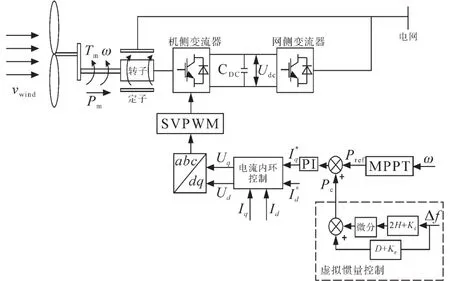
圖1 風電系統模型框圖Fig.1 Block diagram of wind power system model

1.1 雙饋風力發電機模型

雙饋風力發電機在同步坐標系下的數學模型[10]為

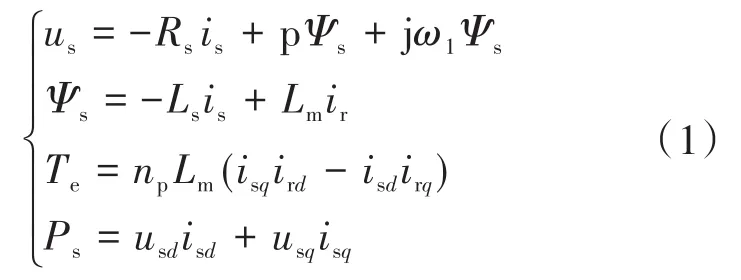
式中：Ψs，Ps，us，is，ir分別為定子磁鏈、定子有功功率、定子電壓、定子電流和轉子電流；p，Ls，Lm，ω1，Rs分別為微分算子、定子自感、定子互感、同步角速度、定子電阻；Te，np分別為電機電磁轉矩和電機極對數。

1.2 最大風能捕獲

風力機從葉片掃過面積中析取風能[11]為

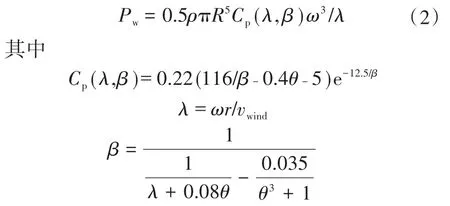
式中：Pw為風力機從風能中析取的機械功率；ρ為空氣密度；R為風機半徑；r為風機葉片長度；ω為系統實際角頻率；vwind為風速；Cp(λ,β)為功率系數，與槳距角θ和葉尖速比λ有關。

調整風機轉速可使Cp(λ,β)達到最優值，記為Cpmax(λ,β)，對應地，葉尖速比則為 λopt。此時風力機析取風能達到最大值，即Pwmax=koptω3，其中，kopt=0.5ρπR5Cpmax(λ,β)/λopt。

1.3 風電系統PD慣量控制

附加功率外環慣量控制結構如圖2所示。

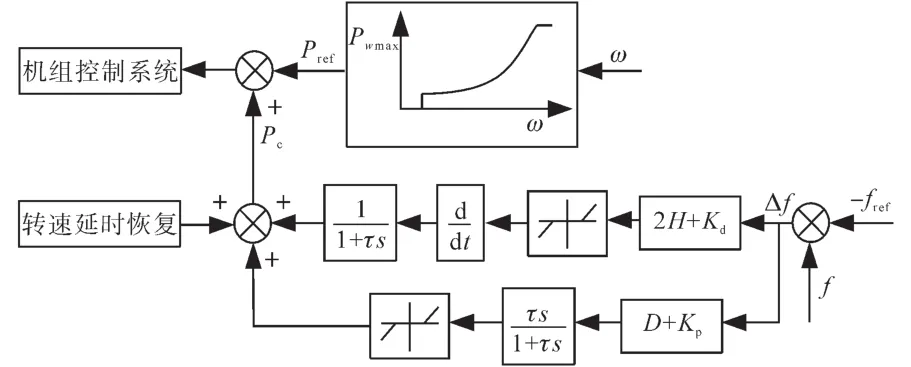
圖2 附加功率外環慣量控制結構圖Fig.2 Inertia control structure of additional power outer loop

引入頻率變化率dΔf/dt和頻率偏差Δf反饋調整轉矩輸出值，并簡化濾波器環節。死區環節只對較大的擾動產生作用，不影響風電機組的穩態運行，也不會降低發電量。

慣量響應目標有功功率如下式：

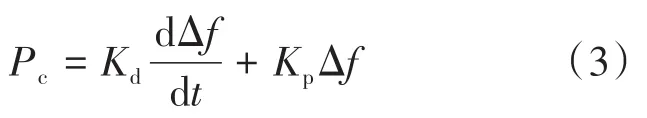
式中：Pc為慣量響應目標有功功率；Kd為微分參數；Kp為比例參數。

為了改善系統頻率的暫態性能，利用儲能系統模擬出的同步發電機慣性響應來增加電力系統的等效慣量。

電力系統的慣量響應[12]可表示為

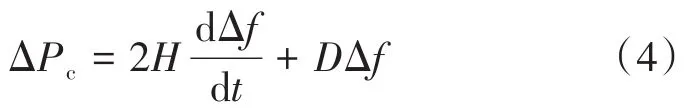
式中：H為虛擬慣量時間常數；D為阻尼。

考慮風電機組的慣量響應則為

2 模糊自抗擾儲能慣量控制

風電場系統結構如圖3所示。

圖3 風電場系統結構圖Fig.3 Wind farm system structure

2.1 模糊自抗擾控制器設計

設計的模糊自抗擾控制器如圖4所示。

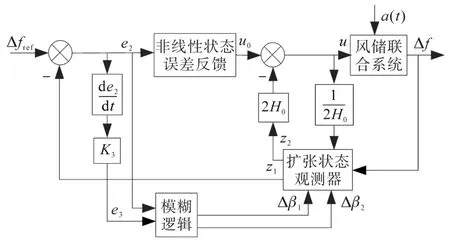
圖4 模糊自抗擾控制器結構框圖Fig.4 Structure diagram of FLC-ADRC

2.1.1 擴張狀態觀測器（ESO）

當電力系統發生負荷擾動后，標準一階系統形式的系統頻率動態響應[13]可表示為

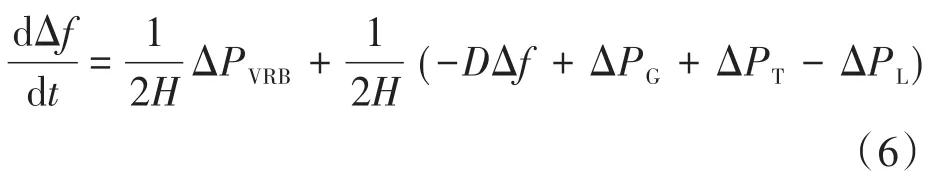
式中：PG為常規同步發電機提供的功率；PVRB為儲能虛擬慣量控制所產生的有功功率增量參考值；PT為相鄰系統間的交換功率；PL為系統有功負荷；ΔPG，ΔPVRB，ΔPT，ΔPL為相對應的增量。

若知H值的估計值為H0，則式（6）改寫成：

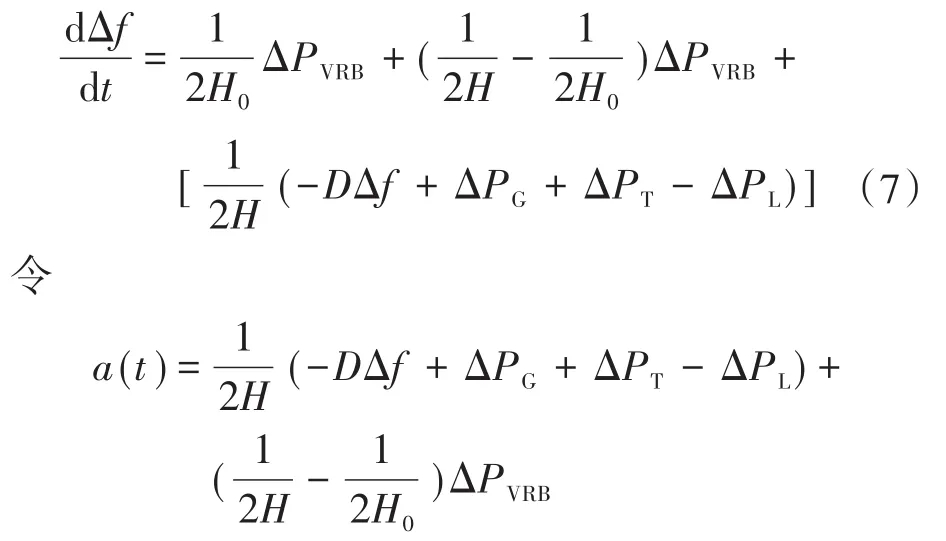
則式（7）可改寫成：

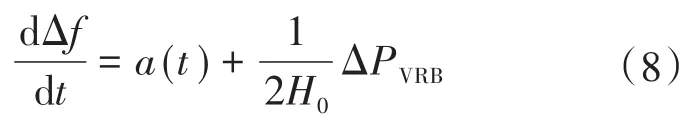
式中：a(t)為所有總有功不平衡（不包括儲能系統）對dΔf/dt的干擾。

為補償系統有功功率不平衡，可采用儲能虛擬慣量控制方法，對應地設計為

式中：KVRB為儲能系統慣量響應參與系數，其取值范圍為0≤KVRB≤1。

加入模擬同步發電機一次調頻的有功功率參考增量，則式（9）變為

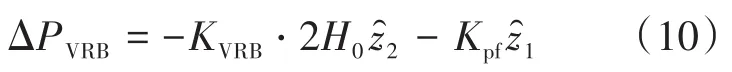
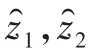
式（10）模擬了同步發電風機的慣量響應和一次調頻特性。

基于式（8），令狀態變量x=Δf，控制輸入u=ΔPVRB，系統未知總擾動為a(t)，則可得：

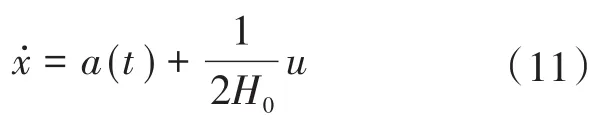
依據式（11）可用ESO來對狀態變量x和新的擴張狀態變量a(t)進行非線性估計。于是，令新的狀態變量 z1=x，z2=a(t)，輸出 y=z1=x，ESO可改進為

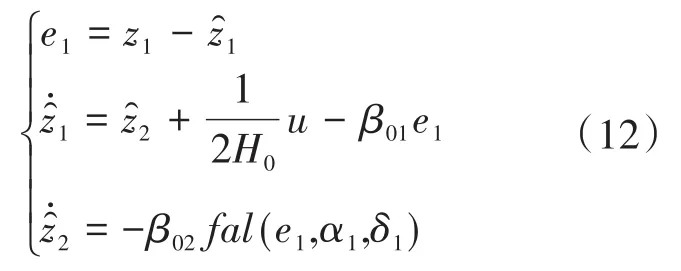
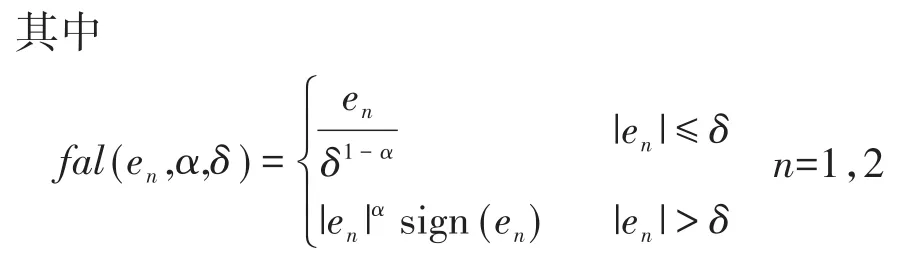
2.1.2 非線性狀態反饋控制器（NSEFL）

非線性狀態反饋控制器可表示為

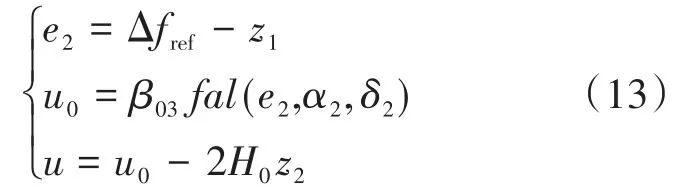
式中：β03為比例系數；u0為控制輸入。

2.2 模糊規則

由于自抗擾控制器的控制性能取決于控制器內部參數，于是，利用模糊規則，在線實時整定其內部參數，以實現自適應控制。將e2和e3（e2的變化率）作為模糊輸入變量，Δβ01，Δβ02分別為模糊輸出變量，利用模糊規則對參數β01，β02進行在線修改。在其各自論域上分別定義5個語言子集為{NB，NS，ZO，PS，PB}。這里取e2，e3的基本論域分別為{-0.2，-0.1，0，0.1，0.2}和{-0.02，-0.01，0，0.01，0.02}，Δβ01，Δβ02的論域為{-0.06，-0.03，0，0.03，0.06}，取K3＝0.000 1。模糊推理采用Mam?dani型，e2，e3的隸屬度函數為三角形（trimf），去模糊化算法采用面積重心法，得到如表1所示的模糊規則表，Δβ01,Δβ02隸屬度函數如圖5所示。

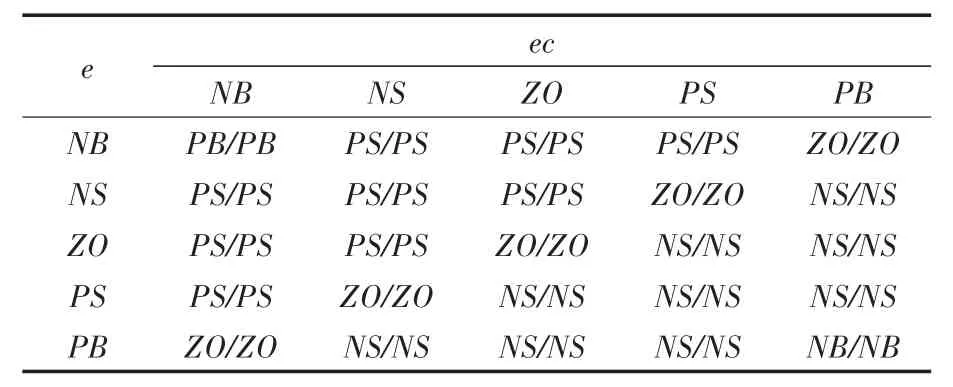
表1 Δβ01,Δβ02的模糊規則表Tab.1 Fuzzy rule table of Δβ01,Δβ02

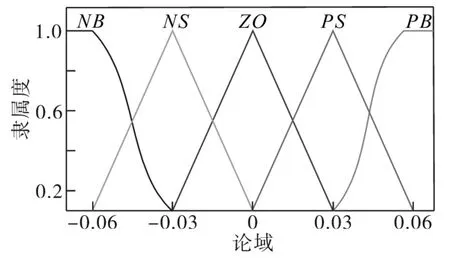
圖5 Δβ01,Δβ02隸屬龐函數Fig.5 Membership function of Δβ01,Δβ02

3 仿真分析

研究系統單線圖如圖6所示，雙饋風力發電系統的風電場由500臺單機容量為1.67MV?A的雙饋風機組成，并經過70 km輸電線接入母線1。三臺同步發電機SG1～SG3、原動機調速器、同步機勵磁調節器及輸電線路使用的模型及參數同文獻[14]。在Matlab/Simulink中建立仿真模型，設置在中風速情況下進行，中等風速仿真如圖7所示。

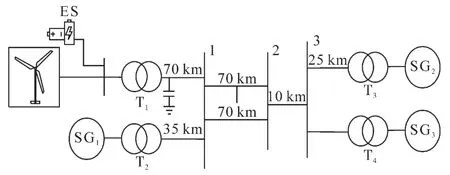
圖6 研究系統單線圖Fig.6 Single line diagram of research system

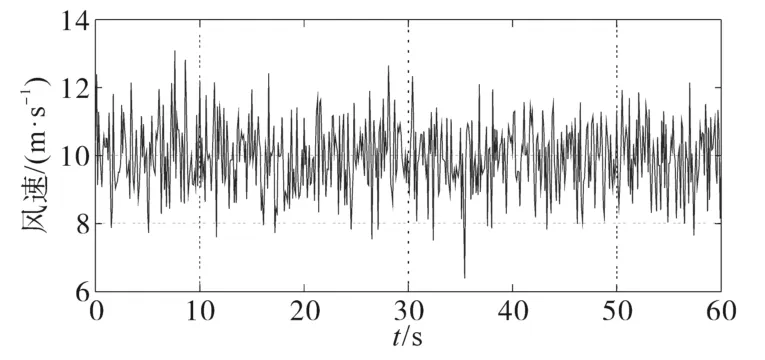
圖7 中等風速仿真結果圖Fig.7 Simulation results of medium wind speed

圖8所示為電網頻率仿真結果，圖9所示為有功功率仿真結果。

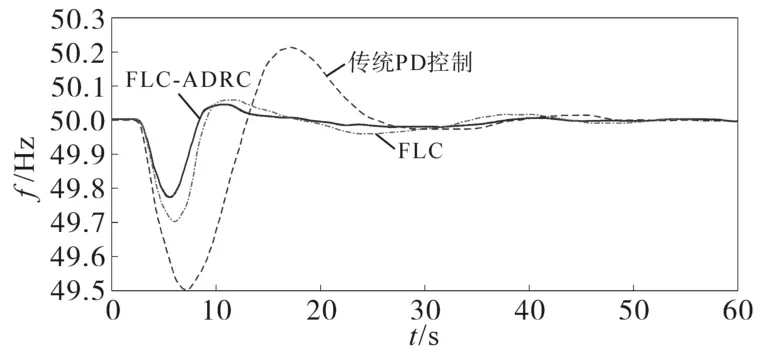
圖8 電網頻率仿真結果圖Fig.8 Simulation results of grid frequency

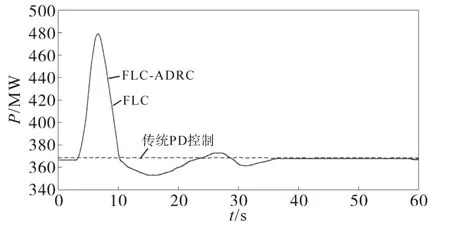
圖9 有功功率仿真結果圖Fig.9 Simulation results of active power

在圖8中，當第6 s負載突增時，傳統PD控制模式下，系統頻率由50 Hz下降到49.5 Hz；基于FLC和FLC-ADRC儲能慣量控制的系統頻率最低值分別下降到49.7 Hz和49.8 Hz，相對于傳統PD控制模式下分別提升了0.4%和0.6%。在圖9中，傳統PD控制模式下有功功率動態過程幾乎不變，而FLC和FLC-ADRC的動態響應相似。分析可知，FLC和FLC-ADRC的儲能慣量控制策略都給系統提供了有效的有功功率支撐，且基于FLC-ADRC儲能慣量控制的電網動態過程較采用FLC明顯改善。

圖10所示為轉子轉速仿真結果，圖11所示為ES輸出功率仿真結果。

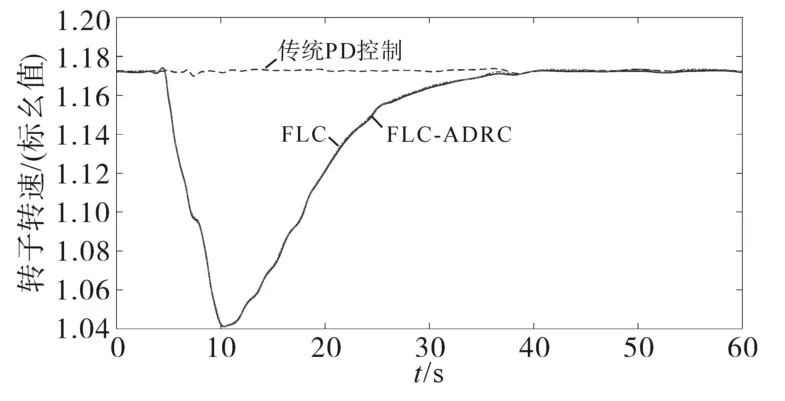
圖10 轉子轉速仿真結果圖Fig.10 Simulation results of rotor speed

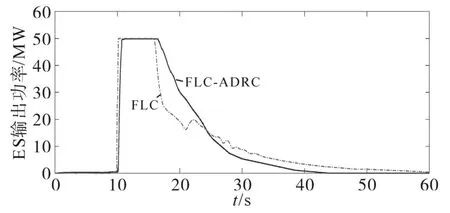
圖11 ES輸出功率仿真結果圖Fig.11 Simulation results of ES output power

在圖10中，傳統PD控制模式下轉子轉速幾乎不變，FLC和FLC-ADRC可通過DFIG轉子轉速降低來釋放動能，進而為頻率提供部分支撐。在圖11中，采用FLC-ADRC儲能慣量控制的ES在10.2 s投入使用，相較于FLC晚0.2 s，FLC的ES控制比FLC-ADRC更早投入使用，FLC中所需的能量大于FLC-ADRC中所需的。因此，FLCADRC儲能系統輸出功率時長相對FLC的時長縮短了。

4 結論

針對轉子與電網頻率解耦，雙饋風電機組無法對系統頻率提供有力支持，本文提出一種基于模糊自抗擾儲能慣量控制方法，在儲能慣量控制方法中引入自抗擾控制器，然而自抗擾控制器內部參數眾多，于是采用模糊規則智能調節擴張狀態觀測器參數，達到為風電場電網頻率提供有效支撐的目的。仿真表明，將模糊控制和自抗擾控制相結合，與模糊虛擬慣量控制方法相比，模糊自抗擾控制能提高系統的動態性能、魯棒性和抗干擾能力，提高電網頻率跟蹤精度。