基于最小熵約束的可解釋卷積神經網絡

石曉榮 倪 亮 王 健 郭宇航

北京控制與電子技術研究所，北京 100038

0 引 言

導彈探測直接影響導彈打擊目標的成功率。導彈武器系統上的光學探測方法必須具備高可靠性，才能保障導彈武器的成功打擊。卷積神經網絡近年來在圖像識別領域取得了較大突破，將卷積神經網絡應用于導彈武器系統有望提升目標探測打擊的成功率，提高武器裝備作戰效能。但是卷積神經網絡屬于“黑盒模型”，在可靠性上不能保證，難以直接應用于導彈武器系統。

當前卷積神經網絡(CNN)的解釋性方面的研究從思路方面可分為2類：1)通過將輸出的結果映射到輸入空間，來理解CNN的決策過程，獲取對于決策起到關鍵性作用的輸入區域；2)對CNN的中間層進行研究，了解CNN內部本身的解釋方式，通過中間層的一般規律解釋模型，不必與輸入之間存在特定的聯系。

在第1個方向中，開創性的工作之一就是 Selvaraju等人提出的Grad-cam方法[1]，使用了Deconvnet，該網絡通過輸入一個選定層的特征圖，重建出最大的激活單元，通過該方法找出對于該激活單元貢獻度最大的圖像區域。Olah等人[2]提出了一套工具箱，用于預訓練模型中卷積層編碼信息的可視化。LIME[3]選擇了一種更簡單的處理方式，通過線性模型在樣本局部對原模型進行擬合，分析對樣本分類貢獻度最大的圖像區域，從而給出模型的解釋。Zhang等人[4]提出通過圖結構來描述各卷積層之間的關系，解釋層級之間的語義信息。

在第2類方法中，主要的開創性工作之一是Mahendran等人[5]提出根據給出的CNN的中間層，對原圖進行重構，獲得CNN中每個類的理想樣本，通過梯度的方式從中間層生成了能讓分類分數最高的輸入樣本。Deep Generator Network[6]思路類似，通過給定的神經元，生成最具代表性的樣本。Network dissection[7]為了量化CNN隱層的可解釋性，將大量的圖片輸入網絡模型，挑選出中間層激活程度最高的圖片進行分析，將每個神經元當作一個檢測單元，或進一步作為語義分割單元。

另一方面，一些工作研究當前解釋方法的合理性。Sundararajan等人提出，當前大多數解釋方法違背了2條公理：靈敏度和實現不變性。針對這2條公理，他們提出integrated gradients方法用于解釋模型特征之間的相關性[8]。Kindermans等人同樣也在該方面有相關研究：他們分析了當前用于解釋多層神經網絡的方法，如DeConvNet[9]、Guided BackProp[10]和LRP[7]等，發現這些方法在理論上的不合理性，并提出了2種理論上更合理的用于解釋神經網絡的方法——PatternNet和Pattern Attribution[11]。

目前CNN解釋性方面主要的工作圍繞解釋常規的CNN模型的工作方式，由于CNN模型過于復雜，往往無法得到理想的解釋效果[12-14]。也有一些設計本身具備可解釋性的卷積神經網絡，譬如Gabor卷積核[15]，但是往往得到的識別模型性能損失較大。本文設計一種具有高可解釋性的卷積神經網絡，同時保證識別模型的性能不會有較大損失。本文利用最小熵約束，通過可解釋特征的評分來對識別模型給出解釋，模型有較高可解釋性，并且保證了模型的識別性能。

1 提出的方法

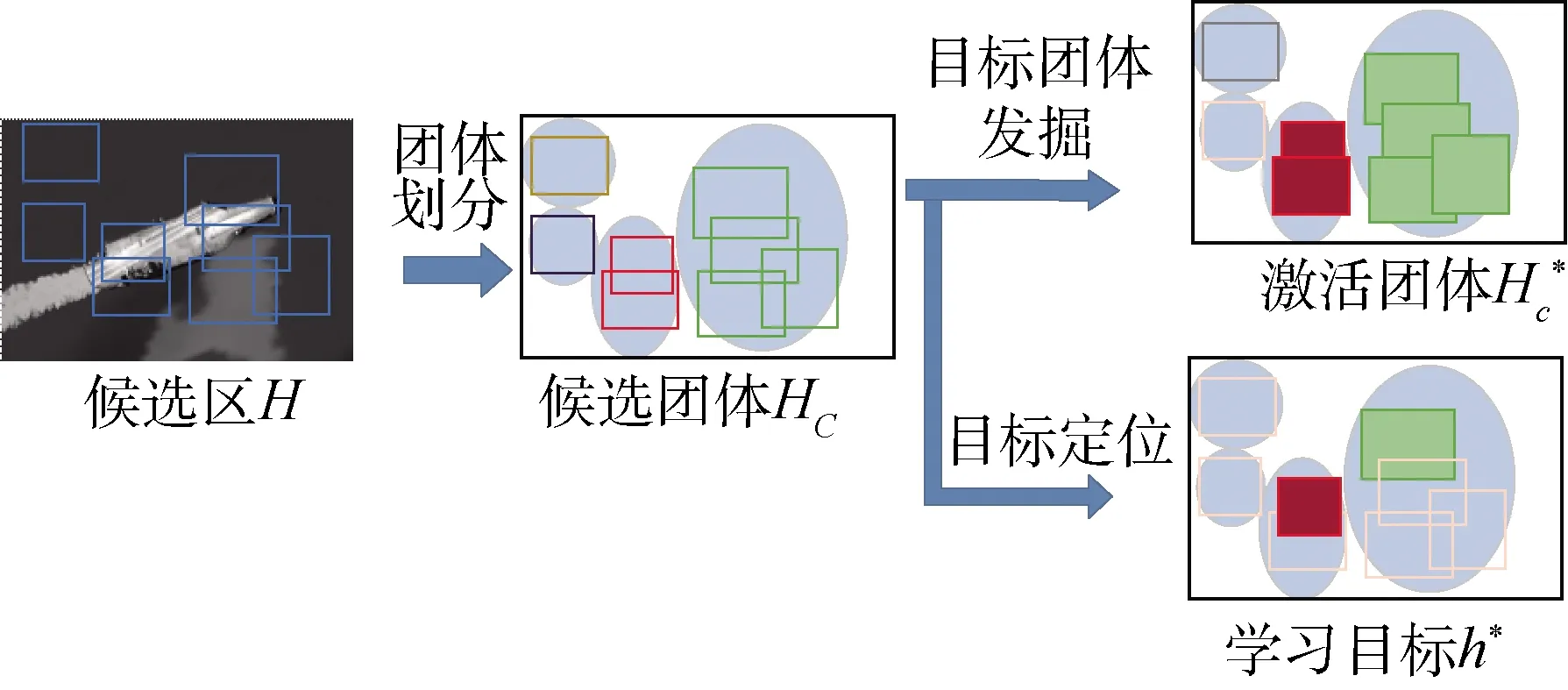
圖1 整體方法思路

本文提出的網絡模型，如圖2所示。h表示一個目標候選區，是一個隱變量。θ表示網絡參數。根據目標團體與目標的位置，聯合圖像標簽，基于全局最小熵與局部最小熵，計算候選區分類損失和目標檢測損失。目標的位置h*和網絡參數θ*，可定義為：

圖2 模型結構

(1)

其中，x代表一幅圖像，y代表x這個圖像里是否包含一個目標。E(x,y)(HC,θ)、E(x,y,HC)(h,θ)分別代表全局和局部的熵模型，α是權重。

根據圖像級分類損失、候選區分類損失、目標檢測損失，對網絡模型進行訓練。本方法模型提取的特征圖，目標區域與背景區域有較大差異，從而模型具有較高的可解釋性。

1.1 候選團體劃分

對輸入圖片使用ROI提取方法，獲得大量的目標候選區域，其中有些候選區域表示目標，有些候選區域表示噪聲，對候選區域進行聚類劃分，有助于可解釋網絡的設計。

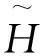
候選區團體可通過以下公式來表示：

(2)

C是候選區團體的數量(劃分團體的過程相當于一個聚類過程)。為了便于劃分，根據候選區的目標分數排序，然后按以下2個步驟進行迭代： 1)選擇得分最高但是還未屬于任何一個團體的候選區組成一個新的團體； 2)將與待觀察的團體中的任何一個候選區的重合面積超過一定閾值的候選區放入待觀察的團體里面去。

1.2 全局最小熵約束

在訓練過程中，要求這些團體以最小的隨機性進化。同時，還需要發現那些包含目標和目標部分區域的有區別的團體。這些團體可以通過激活真正的目標部分來微調網絡參數。為此，定義了一個全局最小熵模型：

(3)

p(y,HC;θ)是一個類別概率，它是根據團體HC的目標分數s(y,HC;θ)定義的：

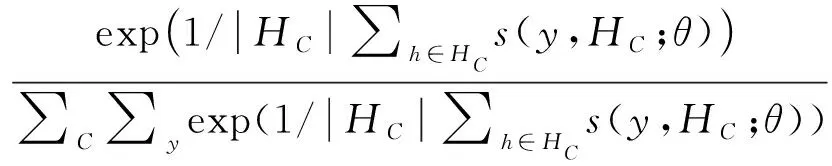
(4)

|HC|可以用來計算一個團體中候選區的數量。s(y,HC;θ)是目標團體分支中的最后一個全連接層輸出的候選區的分數。為了確保被發現的團體能夠最好地從圖像中區分出，我們進一步引進一個與分類相關的權重ωHC。基于候選區的目標類別概率與其圖像類別概率相關的知識，可定義全局最小熵為：

(5)

利用上述定義，我們在網絡頂部實現了一個目標團體分支，如圖2所示，并定義了一個學習網絡參數的損失函數:

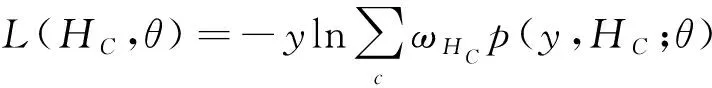
(6)

對數損失，即對數似然損失，是在概率估計上定義的。可用于評估分類器的概率輸出。對于二分類問題，設y∈{0,1}且p=Pr(y=1)，則對每個樣本的對數損失為：

Lln(y,p)=-lnPr(y|p)
=-(yln(p)+(1-y)ln(1-p))

(7)

對于有目標圖片，第2項為0，只有全局最小熵項優化。對于沒有目標圖片，第1項為0，第2項(圖像分類損失)優化。(從公式看，y=0時，loss的目標也是讓p最小，因為p代表一個候選區是某個類的概率，而當y≠0時，p代表不是某個類的概率)

1.3 局部最小熵約束

由全局最小熵模型發掘的團體可以使目標定位有良好的初始化，但同時也包含了隨機誤報，例如目標的部分區域和/或一些帶有背景的部分的局部目標。這由目標團體的學習目標導致，該學習目標用候選區區分有目標圖像和沒有目標的圖像，而沒有考慮如何精確地定位對象。所以提出一個局部的最小熵定位模型，用于精確定位目標。

(8)

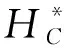
(9)

根據經驗通常讓α=0.6。

根據定義的偽目標和難負目標，目標檢測器的損失函數被定義為：

Ll=-lnf(h*,θ)

(10)

其中f(h*,θ)表示在目標定位分支當中目標檢測器的全連接層以及softmax層。

2 仿真校驗

本次實驗數據集選擇為視覺領域常用數據集PASCAL VOC 2007。本實驗中采用了VGG16作為模型主干網絡，該模型用于對圖片分類，通過深度堆積的卷積層，對圖片進行特征提取，再通過全連接層完成對圖片的分類。

另一方面，通過selective search[16]方法篩選出大量的候選區，再通過ROI Pooling[17]方法將框選出來的特征圖轉化為固定的尺寸，送入后續的全連接結構計算。按照上面提到的方法，獲得的特征圖送入2個分支：一個為全局的最小熵模型，將處理后的候選區送入2個全連接層，第1個全連接層預估每個候選區的類別概率，即判斷當前區域內包含物體的可能性，再在類別維度上進行softmax處理，將其轉化為概率值；另一個分支用于預測每個候選區內是否包含物體，獲得2個分支之后對其進行元素級別相乘，最終獲得的分值同時包含了物體的定位信息以及分類信息。再結合圖片的標簽計算交叉熵損失函數。

在局部最小熵的函數中，通過全局熵模型獲得的分值，定義“偽目標”的標簽，再根據該標簽訓練局部最小熵模型。

評測模型的分類性能，具體評測結果見表1。

表1 模型各類別分類準確率

文中使用的VGG16初始模型通過在ImageNet上預訓練完成后獲得，原VGG16模型在ImageNet上完成預訓練之后，在PASCAL VOC 2007上fine-tune后的分類結果為0.869。本文提出的方法得到的準確率為85%，雖有略微下降，但在可接受范圍之內。

在導彈武器系統對海打擊的應用中，艦船目標的探測識別起到至關重要的作用。使用本文提出的可解釋卷積神經網絡，在光學艦船仿真圖像上訓練模型。該模型在光學艦船仿真圖像上測試，艦船目標的識別率為95.2%。

在導彈對海打擊應用中，仿真艦船樣例如圖3所示，可解釋識別模型在給出分類預測的同時，還會給出圖片中各個區域對識別結果的貢獻度，如圖4所示。貢獻度最高的區域為艦島、船頭部分。根據貢獻度對各區域進行排序，便可以根據最小的區域獲得盡可能大的分類貢獻度。

圖3 仿真艦船測試樣例

圖4 不同圖片區域及對應貢獻度

3 結 論

針對導彈武器系統對光學探測算法高可靠性的要求，提出一種基于最小熵約束的可解釋卷積神經網絡，用于設計可解釋的對海光學探測的智能目標識別模型，為卷積神經網絡模型在導彈武器系統上的應用創造了條件。用傳統方法(連通域檢測、邊緣檢測等)找到圖片中存在的可解釋特征，用模型對可解釋特征進行評分、聚類，并通過這些特征對原模型訓練提供約束，在最終預測的同時，用評分解釋模型。實驗驗證表明，基于最小熵約束模型的可解釋網絡在對分類性能影響程度不大的情況下(使用VGG16分類網絡在PASCAL VOC2007數據集上分類準確率從87%下降到85%)，能夠給出合理的分類依據。在彈載條件下的光學艦船仿真圖像上，本方法可以獲得95.2%的準確率，根據不同區域的貢獻度，可判斷本方法具備可解釋性。