J-正則模與J-正則環

向躍明， 萬欣

（懷化學院數學與計算科學學院，湖南懷化418000）

1 引言

在本文中，R是有單位元的結合環，所有的模都是酉模.除非另外提到，M表示一個左R-模，M*=HomR（M，R）.映射都記在右邊.如果M是一個R-模，則M的根rad（M）為M的所有極大子模的交.若M沒有極大子模，則rad（M）=M.J（R）表示R的Jacobson根.我們用N＜M表示N是M的多余子模.對于通常的符號，請讀者參考文獻[1-3].

元素a∈R是（von Neumann）正則元[2]，如果存在元素x∈R使得a=xax.如果一個環R的每個元素都是正則的，那么它稱為正則環.類似于von Neumann正則環的元素定義，Zelmanowitz[4]稱R-模M正則，如果對任何x∈M存在α∈M*使得（xα）x=x.元素a∈R稱為半正則[5]，如果存在b∈R使得bab=b，并且ab∈J（R）.環R稱為半正則環，如果環R的每個元素都是半正則的.例子包括所有的正則環，半完全環和右連續環等.此外，Nicholson還引入了一類半正則模，用以推廣正則模和半完全模.一個R-模M的元素x稱為半正則的，如果存在α∈M*使得（xα）2=（xα）并且x-（xα）x∈rad（M）.其給出了這些模的一些刻畫，并證明了一個結構定理.在[6]中，如果R/J（R）是正則的，那么R就稱為J-正則的.這里證明了如果R是J-正則的，則：（1）R是右n-內射的當且僅當R的n-生成的多余右理想到R的任意同態可以擴張到R到R的同態；（2）R是右FP-內射環當且僅當R是右（J，R）-FP-內射，一些已知的結果得以改善.

設R是環，M是R-模.在本文的第二節，我們稱M的一個元素x為J-正則，如果存在α∈M*使得x-（xα）x∈rad（M）.如果模M的每個元素都是J-正則的，則稱其為J-正則模.這類模是半正則模和半局部模的推廣.我們討論了J-正則模的一些性質.第三節專門研究了J-正則環的一些性質.證明了環R是J-正則的當且僅當每一個左R-模是J-正則的.設M是有限生成的J-正則的投射模，我們證明了其自同態環EndR（M）也是J-正則的.在第四節中，我們研究環的幾個擴張，如Morita Context和群環.相應的結論成為推論.

2 J-正則模

定義2.1設M為R-模，rad（M）為M的根.元素x∈M叫做J-正則的，如果存在一個α∈M*使得x-（xα）x∈rad（M）.如果模M的每個元素都是J-正則的，則稱其為J-正則模.

根據定義，半正則模是J-正則模.

引理2.2設M為R-模，且x，y∈M.如果x是J-正則的，y∈rad（M），則x+y是J-正則的.

證明：由假設，存在一個α∈M*使得x-（xα）x∈rad（M）.于是

因此，x+y是J-正則的.

引理2.3設M為R-模，x∈M.如果α∈M*使得x-（xα）x是J-正則的，則x是J-正則的.

證明：因為x-（xα）x是J-正則的，則存在β∈M*使得

（x-（xα）x）-（x-（xα）x）β（x-（xα）x）∈rad（M）.

于是x-（xα+xβ-（xα）（xβ）-（（xα）x）β+（（（xα）x）β）（xα））x∈rad（M）.

令γ=α+β-α（xβ）-β（xα）+α（xβ）（xα）.容易驗證γ∈M*以及x-（xγ）x∈rad（M），這證明了x是J-正則的.

根據文獻[7]，M的一個子模N在M中有一個弱補L，如果N+L=M并且N∩L＜M.

定理2.4設R是環，M是R-模.如果rad（M）＜M，則下述等價.

（1）M是J-正則的；

（2）M/rad（M）是正則的；

（3）M的每個有限生成子模都有一個弱補；

（4）M的每個循環子模都有一個弱補.

證明：（3）?（4）是顯而易見的.為了方便，我們設∶=M/rad（M）.

（4）?（1）令x∈M.由假設，Rx有一個弱補，即存在一個子模L使得Rx+L=M并且Rx∩L＜M.因此，我們有（xα）x+y=x，這里α∈M*，y∈L.于是，x-（xα）x=y∈Rx∩L＜M，進而x-（xα）x∈rad（M）.這證明了M是J-正則的.

例2.5（1）沒有極大子模的模是J-正則模.

（2）若M/rad（M）是半單模，則M是半局部模[7].由上述定理，半局部模是J-正則的.

命題2.6如果M＝○i∈IMi是R-模的直和，則M是J-正則的當且僅當對于每個i∈I，Mi是J-正則的.

證明：必要性是顯而易見的.對于充分性只需證明兩個直和項的情況.因此令M=N○K.

考慮任意x+y∈M，這里x∈N，y∈K.因為N是J-正則的，選擇α∈M*使得x-（xα）x∈rad（N）?rad（M）.擴充α至M，Kα=0.于是（x+y）α=xα，進而（x+y）-（（x+y）α）（x+y）=（x-（xα）x）+（y-（xα）y）.

由假設，y-（xα）y在K中是J-正則的.注意到x-（xα）x∈rad（M），由引理2.2，（x+y）-（（x+y）α）（x+y）在M中是J-正則的.由引理2.3，x+y是J-正則的.

3 J-正則環

定義3.1如果R作為R-模是J-正則的，那么環R就是J-正則的，也就是說，對于R的每個元素x，存在y∈R使得x-xyx∈J（R）.根據定理2.4，環R是J-正則的當且僅當R/J（R）是正則的.

例3.2（1）環R稱為半正則的，如果R/J（R）是正則的，并且冪等元模J（R）提升.故半正則環是J-正則環.

（2）根據文獻[8]，如果R/J（R）是布爾環，則稱R為J-布爾環.因為布爾環是正則的，J-布爾環是J-正則的.

（3）如果R/J（R）是半單環，則環R是半局部的.那么半局部環就是J-正則的.

例3.3（1）令k=Z2，k〈x，y〉是非交換變量x，y的自由代數.設R=k〈x，y〉/yx是k〈x，y〉的商環.再令RΣ是R的泛局部化[9].于是RΣ/J（RΣ）≌k×k是布爾環.所以RΣ是J-布爾環，進而是J-正則的.然而，其冪等元并不模J（R）提升.因此RΣ不是半正則環.

下列結論是J-正則環的一些基本性質，其部分結論來源于文獻[6].環R稱為半本原環，如果J（R）=0.

引理3.4設是一個環.則下列結論成立.

（1）R是正則環當且僅當R是J-正則，半本原環.

（2）R是半正則環當且僅當R是J-正則環且冪等元模J（R）提升.

（3）J-正則環的同態像仍是J-正則環.

（4）環的直積R=∏i∈IRi是J-正則環當且僅當Ri是J-正則環.

（5）如果R是J-正則環，則eRe也是J-正則環，這里e2=e∈R.

（6）如果R是J-正則環，則Mn（R）也是J-正則環（n≥1）.

例3.5設R=Z2×Z4×Z8×…，則R是J-正則環但不是半局部環.

命題3.6設R是J-正則環，則：

（1）對R的任意理想I，J（R/I）=（J（R）+I）/I.

（2）如果f∶R→S是滿環同態，則（J（R））f=J（S）.

證明：（1）顯然（J（R）+I）/I?（R/I）.于是我們有

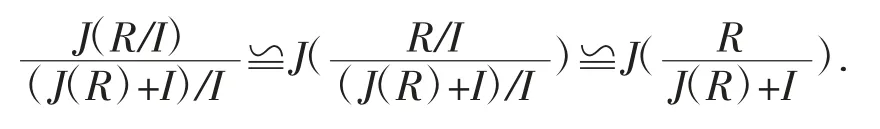
因為R/J（R）+I是正則環R/J（R）的商環，其也是正則環，故

于是，我們有J（R/I）=（J（R）+I）/I.

（2）是（1）的立即結論.

通常地，對任意同態f∶M→N，我們得到（rad（M））f?rad（Mf）.R-模M稱為good模[3]，如果（rad（M））f=rad（Mf）.由命題3.6，J-正則環是左good環.

命題3.7設I是R的理想，I∈J（R），則R是J-正則環當且僅當R/I是J-正則環.

證明：必要性由引理3.4（3）可得.現證充分性，假設R/I是J-正則環，我們有

因為J-正則環是正則的.于是，正則的即是J-正則環.

推論3.8設I是環R的詣零理想，則R是J-正則環當且僅當R/I是J-正則環.

命題3.9設I是環R的理想，則下述等價：

（1）R/I是J-正則環；

（2）對所有自然數n，R/In是J-正則環；

（3）對某些自然數n，R/In是J-正則環.

證明：（2）?（3）是顯然的.

（1）?（2）設R/I是J-正則環.易證明對任意自然數n，（I/In）n=0.注意到R/I≌（R/In）/（I/In），根據推論3.18，R/In是J-正則環.

（3）?（1）若對某些自然數n，R/In是J-正則環.我們定義映射φ∶R/In→R/I.容易證明其是定義良好的環同態.于是根據引理3.4，結論成立.

命題3.10對環R，下述等價：

（1）R是J-正則環；

（2）每個R-模是J-正則.

證明：（2）?（1）是平凡的.

（1）?（2）對任意R-模M，存在集合Λ和滿同態R（Λ）→M.因為

故有滿同態f∶（R/rad（R））（Λ）→M/rad（M）.根據假設和文獻[4]中定理2.8，（R/rad（R））（Λ）是正則的，進而M/rad（M）正則的.再根據定理2.4，M是J-正則的.

命題3.11設M是投射R-模.如果M是有限生成J-正則的，則自同態環EndR（M）是J-正則環.

證明：由假設，M/rad（M）是正則的且rad（M）＜M.根據文獻[3]中22.2，

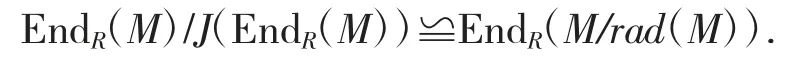
因為M/rad（M）是有限生成正則模，根據文獻[10]中的定理3.6，EndR（M/rad（M））是正則環.故EndR（M）/J（EndR（M））是正則的，進而EndR（M）是J-正則環.

現在，文獻[6]中的定理8可以作為我們結論的推論.

推論3.12設R是J-正則環，M是有限生成投射R-模，則自同態環EndR（M）是J-正則環.

4 環擴張

本節中，我們考慮J-正則環的一些擴張.

Morita Context包含二個環A，B，二個雙模AMB，BNA和一對雙模同態φ∶M○BN→A和ψ∶N○AM→B，滿足條件φ（m○n）m′=mψ（n○m′）和ψ（n○m）n′=nφ（m○n′），這里m，m′∈M，n，n′∈N.其例子包含所有2×2矩陣環和所有的上三角矩陣環.

命題4.1設是Morita Context，其中MN?J（A），NM?J（B）.則T是J-正則環當且僅當A，B都是J-正則環.

證明：由文獻[11]中的命題2.6，

注意到MN?J（A），NM?J（B），于是T/J（T）≌A/J（A）×B/J（B）.故T是J-正則環當且僅當A，B都是J-正則環.

推論4.2設R是環.上三角矩陣環Tn（R）（n∈N）是J-正則環當且僅當R是J-正則環.

設R是環，G是群，RG表示群環.我們有環同態ε∶RG→R，Σrgg→Σrg，叫做RG的增廣映射，其核記作△（RG），△（RG）={Σg∈Gag（1-g）∶1≠g，ag∈R}.容易驗證RG/△（RG）≌R.群G稱為局部有限的，如果G的任意有限生成子群是有限的.下列引理可以在文獻[12]中找到.

引理4.3設R是環，G是群.群環RG是正則環當且僅當是R正則的，G是局部有限的且G的任意有限子群的階在R中可逆.

注4.4上述結果不能推廣到半正則環.例如，設群G的階為3.由文獻[5]的例2.14的討論，群環RG不是半局部環.但是，對于J-正則環我們有如下一些結論.

命題4.5設R是環，G是群.如果下述條款成立

（1）R是J-正則環；

（2）G是局部有限群；

（3）G的任意有限子群的階在R中可逆.

則群環RG是J-正則環.

證明：為方便表示，記=R/J（R）.因為G是局部有限群，根據文獻[13]的引理4，J（R）G≌J（RG），故J（RG/J（R）G）=J（RG）/J（R）G.于是，我們有

因為G的任意有限子群的階在R中可逆，則G的任意有限子群的階在R中可逆.注意到仍是正則的，根據引理4.3，RG是正則的，因此RG/J（RG），故RG/J（RG）是正則的，即RG是J-正則環.

命題4.6設R是交換環，G是Abel群.如果群環RG是J-正則環，則

（1）R是J-正則環；

（2）G是局部有限群；

（3）G的任意有限子群的階在R中可逆.

證明：因為RG/△（RG）≌R，由引理3.4，R是J-正則環.類似地作為RG的同態像也是J-正則環.現設n是G的有限子群的階.對任意x?J（R），nx?J（R），故n不是的零因子.再根據文獻[14]中的定理6，J（G）=0G是正則環.再由引理4.3，（2）成立.最后因為n在中可逆，其在R中也是可逆的.命題得證.