復(fù)雜磁化下硅鋼片矢量磁致伸縮特性測(cè)量與模擬*

李 麗， 樊小鵬， 周永言， 張艷麗， 張殿海

(1. 廣東電網(wǎng)有限責(zé)任公司 電力科學(xué)研究院， 廣州 510082； 2. 沈陽(yáng)工業(yè)大學(xué) 電氣工程學(xué)院， 沈陽(yáng) 110870)

隨著人們環(huán)保意識(shí)日益增強(qiáng)，電機(jī)、變壓器等電工設(shè)備的振動(dòng)、噪聲污染等逐漸成為公眾關(guān)心的熱點(diǎn)問(wèn)題[1].電工設(shè)備產(chǎn)生的振動(dòng)噪聲從來(lái)源可分為氣動(dòng)噪聲、機(jī)械噪聲和電磁噪聲，其中電磁噪聲主要源自于繞組與周?chē)┐艌?chǎng)相互作用產(chǎn)生的洛倫茲力和鐵心硅鋼片在交變磁場(chǎng)作用下的磁致伸縮力[2-4].磁致伸縮是指鐵磁材料在被周期變化磁場(chǎng)磁化時(shí)，外形尺寸表現(xiàn)出微小的周期性的伸長(zhǎng)或收縮現(xiàn)象[5].大型電工設(shè)備鐵心尺寸很大，因此磁致伸縮效應(yīng)產(chǎn)生的振動(dòng)噪聲占比也較大.研究鐵心硅鋼片磁致伸縮特性的測(cè)量和建模方法對(duì)設(shè)計(jì)制造低振動(dòng)噪聲電工設(shè)備具有重要意義.

目前，針對(duì)硅鋼片磁致伸縮特性的測(cè)量主要基于應(yīng)變計(jì)測(cè)量法和激光測(cè)振測(cè)量法，這兩種方法在國(guó)際上都有使用，且各有優(yōu)缺點(diǎn).Gong等[6]采用激光測(cè)振法測(cè)量并分析不同交變磁化下硅鋼片磁致伸縮特性，激光測(cè)振法比應(yīng)變計(jì)法精度要高，但是所需要的測(cè)量系統(tǒng)也更加昂貴和復(fù)雜.Zhang等[7]則采用三軸應(yīng)變片對(duì)硅鋼片交變磁場(chǎng)磁化下的磁致伸縮特性進(jìn)行了實(shí)驗(yàn)測(cè)量研究.由于此方法可以同時(shí)采集三個(gè)不同方向上的磁致伸縮隨磁通密度的變化，根據(jù)材料力學(xué)相關(guān)原理可以得到主應(yīng)變的大小和方向，從而得到磁致伸縮特性為各向異性的結(jié)論.2014年，日本學(xué)者Enokizono教授團(tuán)隊(duì)同樣利用三軸應(yīng)變片法測(cè)量并分析了取向硅鋼片的矢量磁致伸縮特性[8]；張艷麗教授團(tuán)隊(duì)利用一套綜合磁特性測(cè)量設(shè)備，采用三軸應(yīng)變計(jì)作為應(yīng)變檢測(cè)傳感器，分別測(cè)量了硅鋼片交變磁化、旋轉(zhuǎn)磁化以及直流偏磁下的磁致伸縮特性[9-11].測(cè)量結(jié)果表明，取向和無(wú)取向硅鋼片的磁致伸縮均表現(xiàn)出各向異性特性，與磁特性相類(lèi)似，磁致伸縮特性具有矢量和滯后雙重特性.

為計(jì)及硅鋼片磁滯和頻率對(duì)磁致伸縮特性的影響，Zhu等[12]提出了基于神經(jīng)網(wǎng)絡(luò)的磁致伸縮模型，實(shí)驗(yàn)結(jié)果表明，磁致伸縮的滯后特性對(duì)計(jì)算結(jié)果有很大影響，在計(jì)算中應(yīng)予考慮.Wakabayashi等[13]在描述矢量磁特性的Enokizono & Soda模型基礎(chǔ)上，提出了描述矢量磁致伸縮特性E&S-W數(shù)學(xué)模型；李強(qiáng)[14]和周航[15]分別利用交變和旋轉(zhuǎn)磁化下磁致伸縮的測(cè)量數(shù)據(jù)建立了相應(yīng)的動(dòng)態(tài)矢量模型.綜上，國(guó)內(nèi)外學(xué)者在不同磁化情況下磁致伸縮特性模擬方面取得了豐富的研究成果，但是考慮非正弦磁化下的硅鋼片磁致伸縮模型的研究尚未開(kāi)展.

本文針對(duì)單片無(wú)取向硅鋼片在非正弦磁場(chǎng)磁化下的矢量磁致伸縮特性展開(kāi)測(cè)量和模擬方法的研究.基于現(xiàn)有磁致伸縮特性測(cè)量系統(tǒng)，測(cè)量并分析幾種典型高次諧波磁場(chǎng)對(duì)磁致伸縮特性的影響.從頻域角度推導(dǎo)出表征非正弦磁場(chǎng)磁化下的磁致伸縮特性動(dòng)態(tài)矢量數(shù)學(xué)模型，同時(shí)給出相應(yīng)的模型參數(shù)數(shù)據(jù)庫(kù)的建立方法，并驗(yàn)證了模型的有效性.

1 硅鋼片矢量磁致伸縮特性測(cè)量

1.1 測(cè)量方法

為了得到硅鋼片矢量磁致伸縮特性，本文采用基于三軸應(yīng)變花傳感器的磁致伸縮測(cè)量系統(tǒng)來(lái)獲取不同方向的磁致伸縮特性，整體測(cè)量系統(tǒng)組成如圖1所示.為簡(jiǎn)化實(shí)驗(yàn)測(cè)試平臺(tái)的搭建，同時(shí)考慮到測(cè)量結(jié)果的一致性，測(cè)量系統(tǒng)中的勵(lì)磁部分沿用實(shí)驗(yàn)室現(xiàn)有的德國(guó)Brockhaus硅鋼片單片磁特性測(cè)量系統(tǒng)，系統(tǒng)主機(jī)可以控制激勵(lì)形式，實(shí)現(xiàn)在被測(cè)樣片中產(chǎn)生疊加不同諧波的交變磁場(chǎng).勵(lì)磁繞組形成一個(gè)空間有限的內(nèi)腔，測(cè)量時(shí)將待測(cè)樣片置于內(nèi)腔內(nèi).本文采用的測(cè)量樣片牌號(hào)為B50A600無(wú)取向硅鋼片.

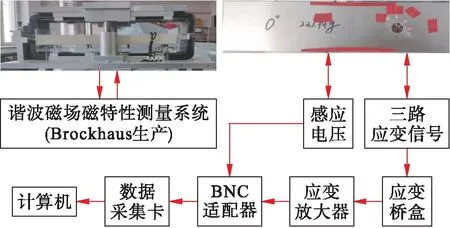
圖1 矢量磁致伸縮特性測(cè)量系統(tǒng)框圖Fig.1 Block diagram of measurement system of vector magnetostriction characteristics

由于硅鋼片磁致伸縮主應(yīng)變的方向和磁化方向不一致，單純檢測(cè)磁化方向的磁致伸縮形變并不能準(zhǔn)確獲取樣品內(nèi)主應(yīng)變的特性.因此采用三軸應(yīng)變花拾取樣片的應(yīng)變信號(hào).考慮到測(cè)量區(qū)域面積和測(cè)量參數(shù)，應(yīng)變花采用日本共和公司生產(chǎn)的產(chǎn)品，其型號(hào)為KFG-10-120-D17-11.為后面數(shù)據(jù)處理方便起見(jiàn)，固定應(yīng)變花時(shí)，應(yīng)保證其長(zhǎng)度方向與硅鋼片的軋制方向一致.這樣，通過(guò)三通道動(dòng)態(tài)應(yīng)變儀就能同時(shí)檢測(cè)硅鋼片沿軋制、垂直于軋制和45°三個(gè)方向的磁致伸縮形變信號(hào)，通過(guò)材料力學(xué)的相關(guān)原理，可以得到磁致伸縮伸長(zhǎng)主應(yīng)變或收縮主應(yīng)變以及對(duì)應(yīng)的主應(yīng)變.

1.2 測(cè)量條件與結(jié)果

由于硅鋼片磁特性的各向異性，不同磁化方向上的磁致伸縮特性也各不相同.但是所使用的磁特性測(cè)量裝置為一維測(cè)量裝置，只能產(chǎn)生單方向的激磁力.為了解決這一問(wèn)題，測(cè)量總共準(zhǔn)備7種樣品，切割方向從軋向到垂直于軋向，間隔15°進(jìn)行.測(cè)量時(shí)，與硅鋼片磁特性測(cè)量標(biāo)準(zhǔn)一致，選擇基波磁通密度幅值作為控制目標(biāo)，設(shè)定值為0.5～1.6 T，步長(zhǎng)為0.1 T.諧波磁場(chǎng)是在上述磁特性測(cè)量系統(tǒng)基礎(chǔ)上開(kāi)發(fā)實(shí)現(xiàn)的，可指定諧波次數(shù)和諧波占基波的百分比以及初相位.此外，該系統(tǒng)還可實(shí)現(xiàn)任意磁通密度波形的輸入.

1.2.1 磁通密度和磁化方向?qū)χ鲬?yīng)變的影響

圖2給出了磁化角度為30°，10%的3次諧波注入時(shí)，不同基波磁通密度幅值下磁致伸縮主應(yīng)變特性.主應(yīng)變幅值隨著基波磁密的增加而增加，而波形特征在樣品飽和之前幾乎沒(méi)有變化.在同一磁化方向上主應(yīng)變角度幾乎不隨磁密的增加而發(fā)生改變.圖3比較了不同磁化方向的主應(yīng)變特性，其中，3次諧波占基波幅值的10%，基波磁密幅值為1.0 .從圖3中可以看出，磁化角度由0°增加到60°時(shí)，磁致伸縮主應(yīng)變幅值隨著磁化角度的增加而增加.其中，軋制方向與15°磁化方向主應(yīng)變幅值較接近，30°和45°磁化方向磁致伸縮增加亦不明顯，60°磁化方向主應(yīng)變幅值最大.

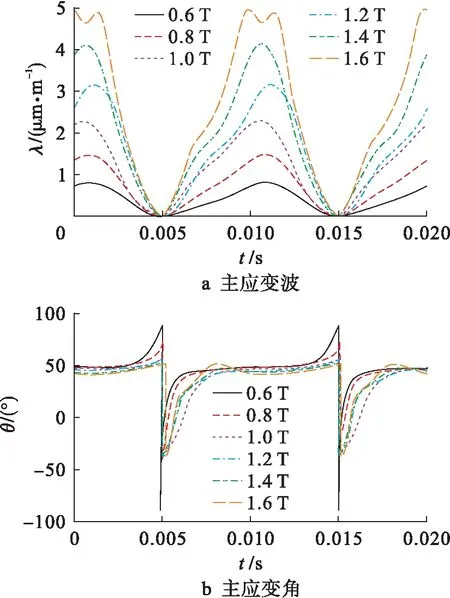
圖2 3次諧波注入時(shí)的主應(yīng)變特性Fig.2 Principal strain characteristics with injection of 3rd harmonics

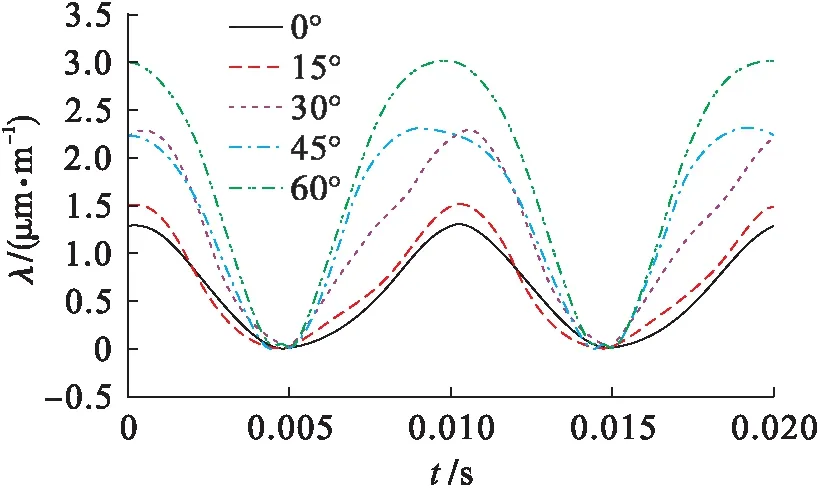
圖3 3次諧波注入時(shí)不同磁化方向的主應(yīng)變特性

1.2.2 諧波占比對(duì)主應(yīng)變的影響

電工設(shè)備實(shí)際運(yùn)行時(shí)，鐵心中不同部位磁場(chǎng)的諧波含量亦不相同，本節(jié)分析不同諧波占比對(duì)磁致伸縮主應(yīng)變特性的影響.

利用1.1節(jié)介紹的測(cè)量裝置分別測(cè)量了諧波含量為8%和6%的3次諧波磁場(chǎng)作用下的磁致伸縮形變，并計(jì)算了主應(yīng)變特性，如圖4所示.從圖4可以看出，在相同的基波磁密下，諧波含量越高，磁致伸縮應(yīng)變峰值越大.隨著諧波含量的減小，應(yīng)變?cè)黾拥内厔?shì)沒(méi)有改變；隨著磁通密度峰值的增加主應(yīng)變峰值仍然增加；在接近飽和時(shí)，應(yīng)變波形變得不再光滑，這說(shuō)明此時(shí)主應(yīng)變波形中的諧波含量更加豐富，呈現(xiàn)非線性特征.

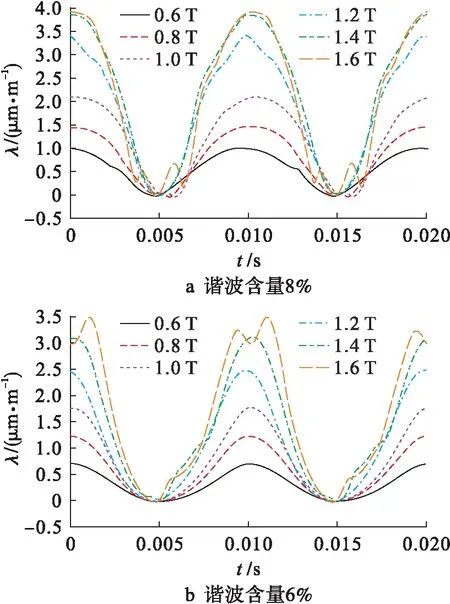
圖4 45°磁化方向上的主應(yīng)變特性Fig.4 Principal strain characteristics along 45° magnetization direction

1.2.3 諧波階次對(duì)主應(yīng)變特性的影響

根據(jù)測(cè)量數(shù)據(jù)，圖5給出了在含有不同階次高次諧波時(shí)，磁致伸縮主應(yīng)變幅值λ隨磁通密度幅值以及磁化方向變化的關(guān)系.從圖5中可以看出，磁致伸縮應(yīng)變的峰值λ不僅和磁化角度有關(guān)，還與磁通密度幅值密切相關(guān)，隨著磁化角度和磁通密度增加而增加.而且，隨著諧波階次的增加和多次諧波同時(shí)存在時(shí)，硅鋼片磁致伸縮主應(yīng)變逐漸增大，在只含有3次諧波時(shí)，隨著磁化角度和磁通密度峰值的增加，磁致伸縮主應(yīng)變?cè)黾酉鄬?duì)平滑.而在只含有5次諧波和3、5次諧波共存下，隨著磁通密度和磁化角度增加，磁致伸縮主應(yīng)變變化不再平滑，這是由于隨著諧波次數(shù)的增加，磁致伸縮主應(yīng)變中更高次諧波含量會(huì)增加，即非線性程度加深.

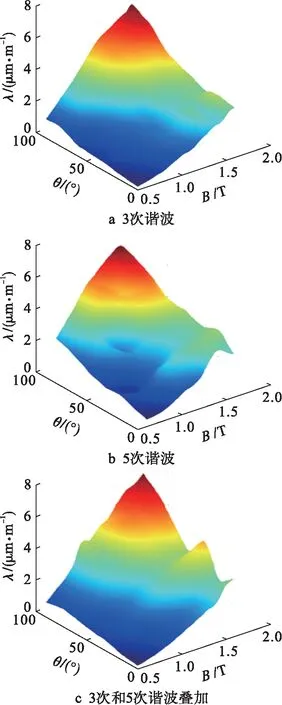
圖5 磁致伸縮主應(yīng)變幅值與磁化條件的關(guān)系Fig.5 Relationship between principal strain magnitude of magnetostriction and magnetization condition

2 動(dòng)態(tài)矢量磁致伸縮模型和參數(shù)計(jì)算

文獻(xiàn)[7]給出了旋轉(zhuǎn)磁化下磁致伸縮主應(yīng)變量和磁通密度矢量的關(guān)系，具體表達(dá)式為

(1)

式中：下標(biāo)x、y分別為x、y方向的物理量；C為磁致伸縮主應(yīng)變的直流分量；Kr和Ki分別為磁致伸縮主應(yīng)變表達(dá)式的系數(shù)；τ=ωt為轉(zhuǎn)角.

考慮到該模型可以描述磁致伸縮的動(dòng)態(tài)時(shí)變特性，接下來(lái)將基于該模型建立非正弦磁化下磁致伸縮的動(dòng)態(tài)矢量特性模型，并根據(jù)諧波磁場(chǎng)磁致伸縮特性，給出相應(yīng)的主應(yīng)變動(dòng)態(tài)矢量模型的參數(shù)數(shù)據(jù)庫(kù)建立方法.

2.1 動(dòng)態(tài)矢量特性模型

非正弦磁化下，磁通密度波形可表示為

(2)

式中：n為第n個(gè)奇次諧波，例如，n=2表示第2個(gè)奇次諧波，即3次諧波，以此類(lèi)推；N為最大奇次諧波個(gè)數(shù)；Bmax為磁通密度的基波幅值；θB為磁化角度；αn為注入的第n次諧波占基波幅值的百分比；φn為第n次諧波的初相位.若將式(2)做進(jìn)一步處理，可表示為

I(2n-1)Bksin(2n-1)τ]

(3)

式中，k=x，y.將式(3)對(duì)τ求導(dǎo)，可以得到

(4)

將式(3)、(4)代入到式(1)中，則λk可以表示為

I(2n-1)Bkcos(2n-1)τ-(2n-1)R(2n-1)Bk·

sin(2n-1)τ]

(5)

考慮到磁致伸縮應(yīng)變波形中包含直流分量和偶數(shù)次諧波，故其傅里葉展開(kāi)形式為

(6)

式中：m為第m個(gè)偶次諧波；M為最大的偶次諧波個(gè)數(shù)；Ck0為磁致伸縮應(yīng)變的直流分量；R(2m)λk、I(2m)λk分別為偶數(shù)次諧波的實(shí)部和虛部.為了確定最高保留諧波的次數(shù)，將測(cè)量的磁致伸縮應(yīng)變波形進(jìn)行傅里葉分解可以總結(jié)出，不論磁密在飽和區(qū)或非飽和區(qū)，大于8次的應(yīng)變諧波分量均可以忽略不計(jì)，因此在后續(xù)建模過(guò)程中僅保留8次以?xún)?nèi)的諧波.基于上述分析，式(6)的磁致伸縮主應(yīng)變表達(dá)式可簡(jiǎn)化為

(7)

比較表達(dá)式(5)、(7)，發(fā)現(xiàn)式(7)中每一項(xiàng)都能在式(5)中找到對(duì)應(yīng)項(xiàng)，于是，只需令對(duì)應(yīng)項(xiàng)的系數(shù)相等，即可得到所提出模型的參數(shù)表達(dá)形式，即

Ck=Ck0

(8)

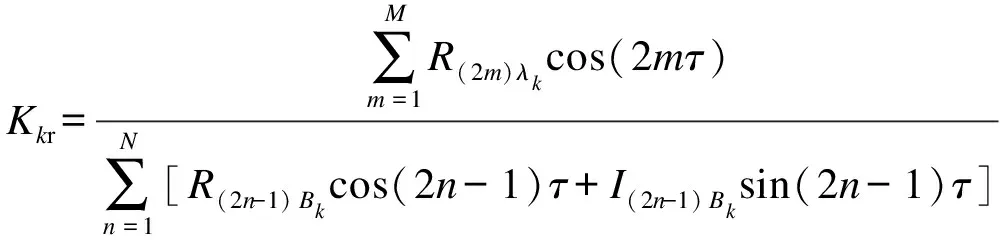
(9)

(10)

式中，參數(shù)Kkr和Kki為τ、θB以及Bm的函數(shù)，可以看到兩模型參數(shù)值受到磁化方式的影響.

2.2 模型的參數(shù)計(jì)算及驗(yàn)證

作為驗(yàn)證，利用上述模型分別計(jì)算了3次諧波磁場(chǎng)注入時(shí)，磁化角度為75°，磁通密度幅值為1.58 T和磁化角度為45°，磁通密度幅值為1.12 T時(shí)的磁致伸縮主應(yīng)變波形.實(shí)驗(yàn)測(cè)試結(jié)果對(duì)比情況如圖6所示，可以看出模擬結(jié)果與實(shí)際測(cè)量數(shù)據(jù)基本吻合.

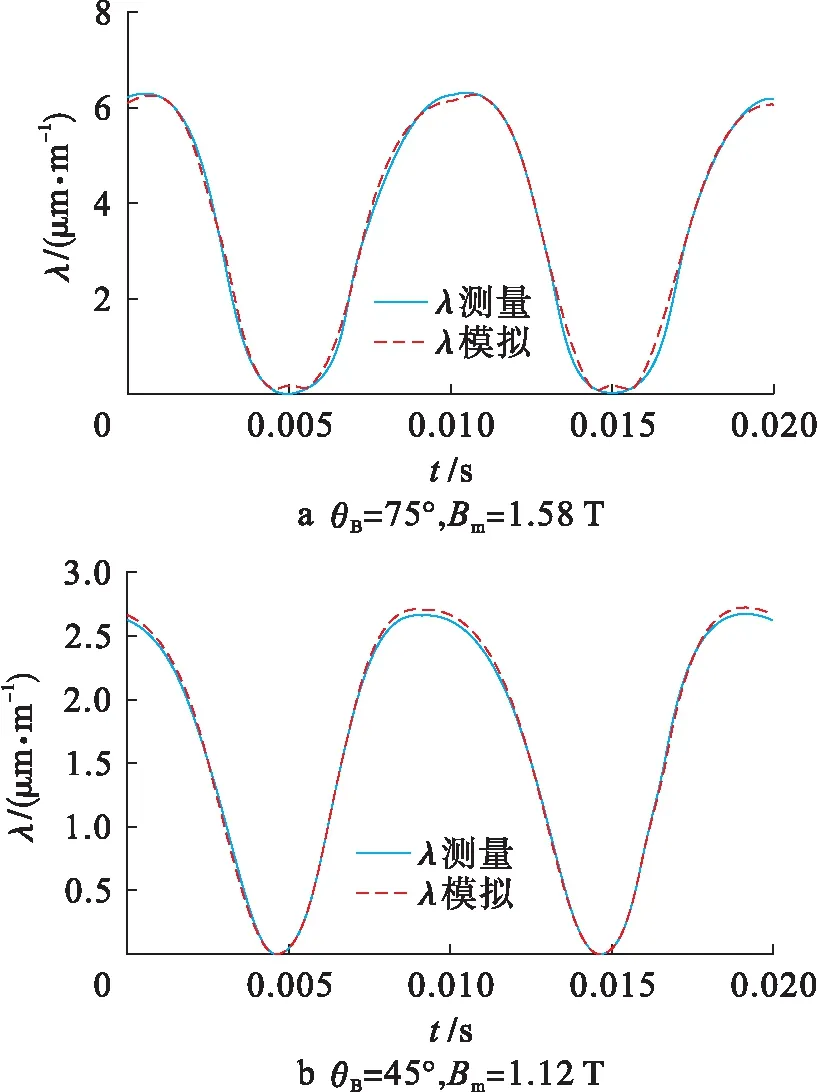
圖6 測(cè)量與模擬磁致伸縮的波形比較Fig.6 Comparison between measured and simulated magnetostriction waveforms

3 結(jié) 論

本文利用實(shí)驗(yàn)室現(xiàn)有一維磁特性測(cè)量設(shè)備結(jié)合三軸應(yīng)變花傳感器及其附屬設(shè)備測(cè)量了非正弦磁場(chǎng)磁化下硅鋼片磁致伸縮特性，通過(guò)材料力學(xué)相關(guān)原理計(jì)算了磁致伸縮主應(yīng)變波形及其主應(yīng)變角，討論了在基波磁場(chǎng)中注入不同階次、不同占比高次諧波磁場(chǎng)時(shí)，磁致伸縮主應(yīng)變的變化規(guī)律.結(jié)合實(shí)驗(yàn)數(shù)據(jù)分析給出了高次諧波磁場(chǎng)作用下磁致伸縮主應(yīng)變動(dòng)態(tài)矢量數(shù)學(xué)模型，推導(dǎo)了模型參數(shù)的計(jì)算表達(dá)式，建立了模型參數(shù)的數(shù)據(jù)庫(kù).最后，通過(guò)與實(shí)驗(yàn)數(shù)據(jù)的比較驗(yàn)證了模型的有效性.得到的結(jié)論如下：

1) 在非正弦磁場(chǎng)磁化下，主應(yīng)變方向和磁化方向不一致，且兩者的夾角隨時(shí)間變化；

2) 注入同一頻率高次諧波條件下，磁致伸縮主應(yīng)變幅值隨著諧波含量的增加而增加，當(dāng)磁場(chǎng)接近飽和時(shí)，磁致伸縮主應(yīng)變也相應(yīng)趨于飽和；

3) 諧波含量相同時(shí)，隨著高次諧波次數(shù)的增加，磁致伸縮應(yīng)變峰值也增加，磁致伸縮回環(huán)不再光滑，磁致伸縮諧波含量增大，呈現(xiàn)非線性的特征；

4) 不同的磁化方向也會(huì)影響磁致伸縮主應(yīng)變峰值的變化，隨著磁化角度的增加，磁致伸縮主應(yīng)變峰值與磁化角度呈現(xiàn)出線性增長(zhǎng)的趨勢(shì)，但同時(shí)又表現(xiàn)出各向異性的特點(diǎn)；

5) 磁致伸縮動(dòng)態(tài)矢量數(shù)學(xué)模型可以有效地模擬高次諧波磁場(chǎng)作用下硅鋼片的磁致伸縮特性，模型參數(shù)的表達(dá)式充分考慮了磁化方式的影響.