往復(fù)式壓縮機(jī)氣量調(diào)節(jié)工況下的內(nèi)模解耦PID控制策略研究

洪槐斌，劉雯華，張進(jìn)杰

（北京化工大學(xué) 機(jī)電工程學(xué)院診斷與自愈工程研究中心，北京 100029）

0 引言

往復(fù)式壓縮機(jī)是現(xiàn)代石油化工企業(yè)的常見(jiàn)設(shè)備，基于節(jié)能理念設(shè)計(jì)的往復(fù)式壓縮機(jī)氣量調(diào)節(jié)系統(tǒng)［1］在近年得到了越來(lái)越廣泛的應(yīng)用。在氣量調(diào)節(jié)系統(tǒng)中，連續(xù)的多級(jí)壓縮將氣體提升到額定壓力后排出，造成系統(tǒng)存在多個(gè)控制量，而各個(gè)控制量之間存在一定的耦合，影響系統(tǒng)的控制品質(zhì)，導(dǎo)致排氣壓力產(chǎn)生波動(dòng)。對(duì)此類(lèi)多變量耦合系統(tǒng)來(lái)說(shuō)，常規(guī)的PID控制雖然結(jié)構(gòu)簡(jiǎn)單，但是難以獲得滿(mǎn)意的控制效果。

內(nèi)模控制［2］是一種基于數(shù)學(xué)模型設(shè)計(jì)的控制策略，它在控制系統(tǒng)中引入數(shù)學(xué)模型，將被控對(duì)象、外部干擾和模型之差反饋給系統(tǒng)輸入［3］。當(dāng)存在誤差或者干擾時(shí)，濾波器能抑制干擾或者模型失配引起的實(shí)際輸出與模型輸出之差，使得系統(tǒng)具有較好的設(shè)定值跟蹤性能，又有較好的抗干擾性能和魯棒性。文獻(xiàn)［4］指出內(nèi)模控制結(jié)構(gòu)可以轉(zhuǎn)換為PID形式的標(biāo)準(zhǔn)反饋控制結(jié)構(gòu)，從而構(gòu)成內(nèi)模PID控制器，由于內(nèi)模PID控制器只有一個(gè)與濾波器有關(guān)的調(diào)節(jié)參數(shù)，該參數(shù)的選取直接影響到系統(tǒng)的閉環(huán)時(shí)間常數(shù)和系統(tǒng)的魯棒性。文獻(xiàn)［5］根據(jù)解耦理論通過(guò)串級(jí)前饋時(shí)滯補(bǔ)償器將原系統(tǒng)解耦為多個(gè)單變量小時(shí)滯系統(tǒng)，運(yùn)用了麥克勞林級(jí)數(shù)展開(kāi)式，通過(guò)相應(yīng)項(xiàng)系數(shù)的比對(duì)得到了傳統(tǒng) PID 控制器。文獻(xiàn)［6-7］將內(nèi)模控制和解耦控制結(jié)合應(yīng)用于空調(diào)和燃料電池領(lǐng)域，均取得了較好的控制效果。近年來(lái)，內(nèi)模控制在非線(xiàn)性控制領(lǐng)域也發(fā)揮了重要作用，文獻(xiàn)［8］結(jié)合經(jīng)典的雙環(huán)控制和非線(xiàn)性?xún)?nèi)模控制的優(yōu)點(diǎn)，實(shí)現(xiàn)了永磁同步電機(jī)的寬調(diào)速范圍的速度跟蹤和非線(xiàn)性擾動(dòng)抑制。可見(jiàn)各種經(jīng)過(guò)改良的內(nèi)模控制方法已經(jīng)在工業(yè)應(yīng)用領(lǐng)域越來(lái)越被重視［9-10］。

1 氣量調(diào)節(jié)原理及過(guò)程模型

氣量調(diào)節(jié)系統(tǒng)通過(guò)部分行程頂開(kāi)進(jìn)氣閥的方式調(diào)節(jié)被壓縮的氣體量而達(dá)到降低能耗的目的。本文研究的氣量調(diào)節(jié)系統(tǒng)主體為一臺(tái) 2D 型雙作用往復(fù)壓縮機(jī)，如圖1所示。上游氣體經(jīng)一級(jí)氣缸進(jìn)氣閥進(jìn)入一級(jí)壓縮腔被壓縮后排出暫存至一級(jí)排氣緩沖罐，而后經(jīng)二級(jí)氣缸進(jìn)氣閥進(jìn)入二級(jí)壓縮缸繼續(xù)被壓縮，最后排出到二級(jí)排氣緩沖罐暫存待下游設(shè)備使用。氣量調(diào)節(jié)系統(tǒng)通過(guò)人為調(diào)節(jié)進(jìn)氣閥開(kāi)啟與關(guān)閉的時(shí)間而改變壓縮缸內(nèi)的氣體量，被壓縮氣體越少，機(jī)組做的功越少，所消耗的電能也就越少。

圖1 空氣壓縮機(jī)實(shí)驗(yàn)臺(tái)Fig.1 Air compressor test bench

根據(jù)文獻(xiàn)［11］中往復(fù)壓縮機(jī)的數(shù)學(xué)模型，可以得到各級(jí)進(jìn)氣量的排氣量表達(dá)式：

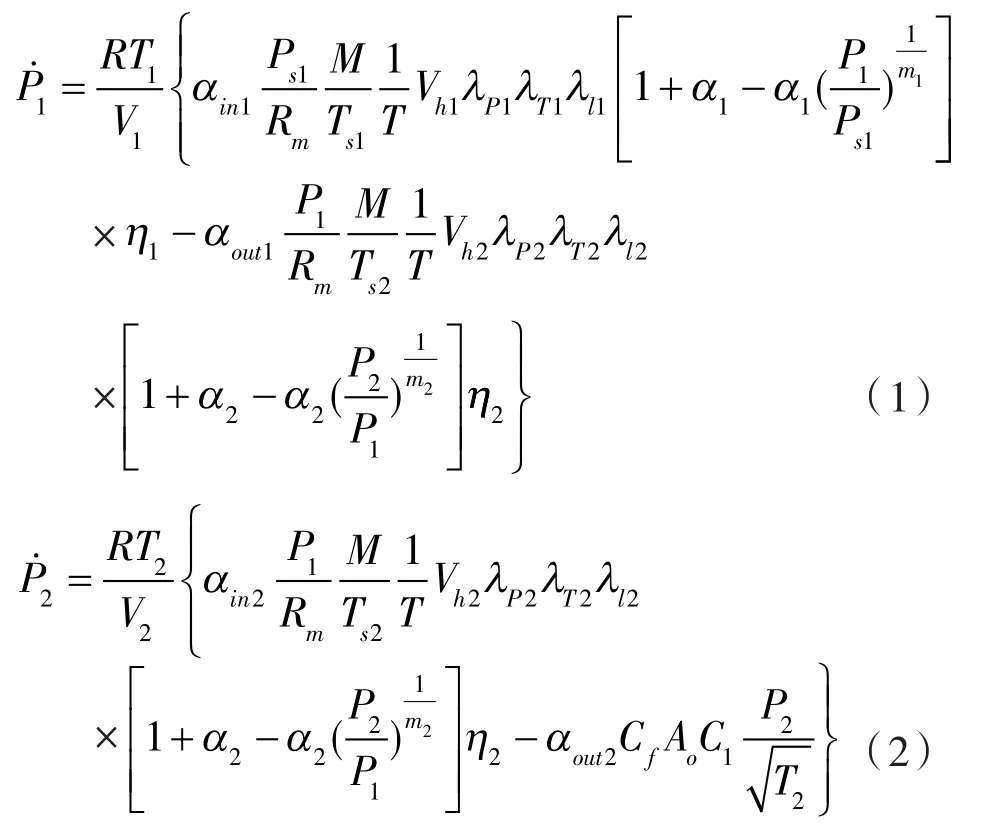
式中 Pi——緩沖罐壓力；

Ti——緩沖罐溫度；

Vi——緩沖罐體積；

Psi——名義進(jìn)氣壓力；

Rm——通用氣體常數(shù)；

Tsi——進(jìn)氣溫度；

T——壓縮機(jī)循環(huán)周期；

Vhi——?dú)飧仔谐倘莘e；

λPi——壓力系數(shù)；

λTi——溫度系數(shù)；

λli——泄露系數(shù)；

αi——容積系數(shù)；

mi——膨脹指數(shù)；

ηi——負(fù)荷值；

Cf——排氣系數(shù)；

Ao——出口閥門(mén)截面；

Ci——各級(jí)氣體系數(shù)（下標(biāo)i=1表示一級(jí)，i=2表示二級(jí)）。

查閱壓縮機(jī)設(shè)計(jì)手冊(cè)，將實(shí)驗(yàn)臺(tái)壓縮機(jī)的設(shè)計(jì)參數(shù)和其他相關(guān)參數(shù)代入式（1）和（2）可得如下壓縮機(jī)排氣壓力和負(fù)荷關(guān)系的微分方程組：

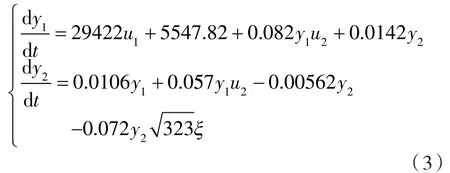
式中 u1，u2——一級(jí)壓力設(shè)定值和二級(jí)壓力設(shè)定值；

y1，y2——一級(jí)排氣壓力與二級(jí)排氣壓力；

ξ——二級(jí)排氣緩沖罐閥門(mén)開(kāi)度。

通過(guò)對(duì)系統(tǒng)進(jìn)行關(guān)聯(lián)性分析可知，該系統(tǒng)存在較大的耦合性，一級(jí)和二級(jí)的某一個(gè)設(shè)定值變化會(huì)對(duì)彼此產(chǎn)生影響。通過(guò)系統(tǒng)辨識(shí)的方法，將閥門(mén)開(kāi)度ξ設(shè)為0.11可以得到系統(tǒng)的過(guò)程傳遞函數(shù)為：

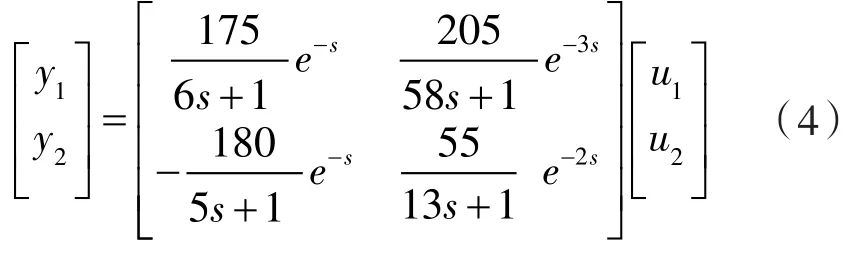
2 內(nèi)模解耦 PID 控制器設(shè)計(jì)

圖2示出一個(gè)經(jīng)典的反饋控制結(jié)構(gòu)，其中Gp（s）為系統(tǒng)開(kāi)環(huán)傳遞函數(shù)，Gc（s）為控制器，r為系統(tǒng)實(shí)際輸出。系統(tǒng)的閉環(huán)傳遞函數(shù)可以表示為：

圖2 單回路反饋控制框Fig.2 Block diagram of single loop feedback control

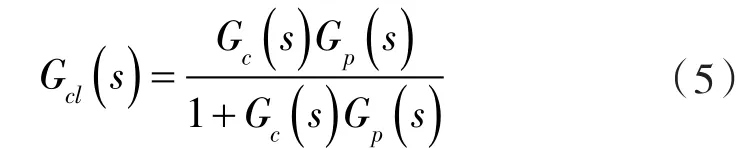
1982年Garcia和Morari完整提出并發(fā)展了圖3示出的內(nèi)模控制結(jié)構(gòu)。Gm（s）為被控過(guò)程數(shù)學(xué)模型，即內(nèi)部模型。Q（s）為內(nèi)模控制器，D（s）表示外部擾動(dòng)對(duì)輸出的影響。r、y和d分別為系統(tǒng)的輸入、輸出和干擾信號(hào)。控制目標(biāo)是保證y逼近設(shè)定值r。

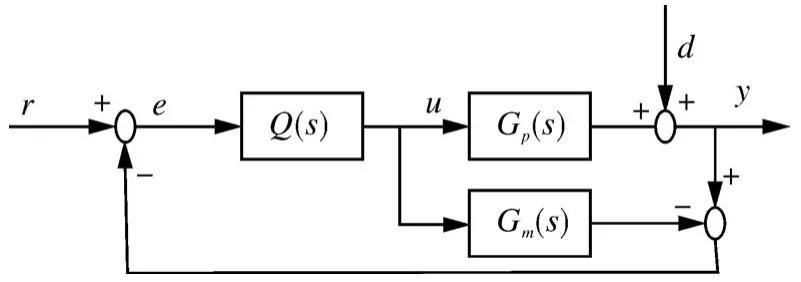
圖3 標(biāo)準(zhǔn)內(nèi)模控制框Fig.3 Block diagram of Standard internal model control

為了求取輸出y和輸入r之間的傳遞函數(shù)，可以將圖3等價(jià)變換為圖4所示的經(jīng)典反饋控制結(jié)構(gòu)，圖中虛線(xiàn)部分為反饋控制器Gc（s）。

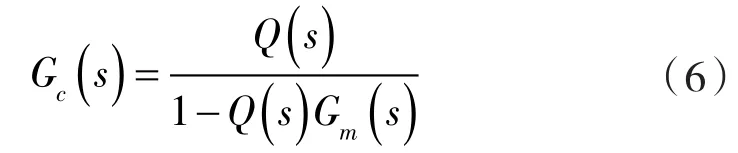
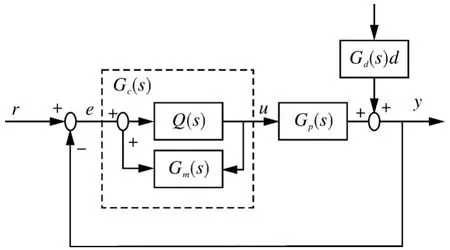
圖4 等效反饋控制系統(tǒng)框Fig.4 Block diagram of equivalent feedback control system

圖4示出的輸入輸出關(guān)系為：

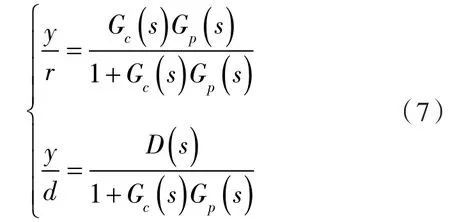
將式（6）代入式（7）得：

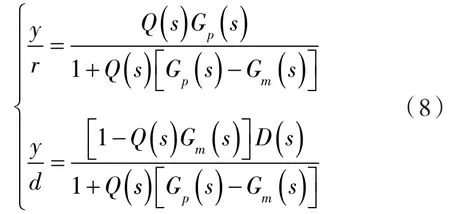
由此可得系統(tǒng)的閉環(huán)響應(yīng)為：

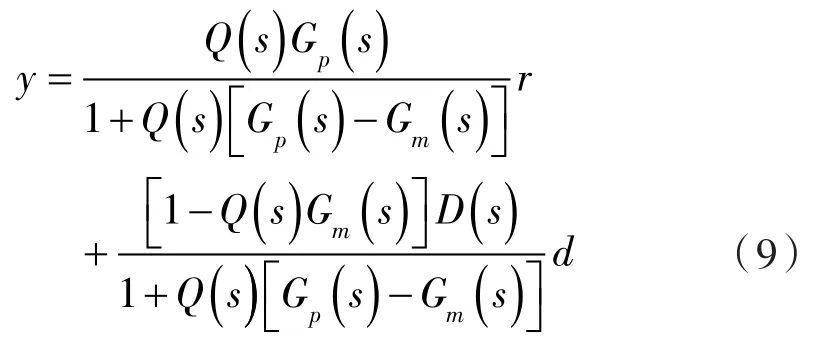
假設(shè)模型是精確的，即 Gp（s）=Gm（s），則有輸出：

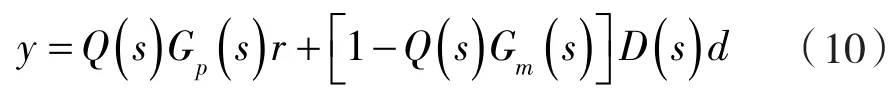
如果選擇：

以上說(shuō)明當(dāng)內(nèi)模控制器選擇為1/Gm（s）時(shí)，控制系統(tǒng)輸出y嚴(yán)格跟蹤系統(tǒng)輸入r。實(shí)際控制系統(tǒng)很難得到精確的數(shù)學(xué)模型，而且有些情況下1/Gm（s）數(shù)學(xué)上是不存在的，所以通常增加相應(yīng)的濾波環(huán)節(jié)構(gòu)成實(shí)際的內(nèi)模控制器［12-15］，具體步驟是先將Gm（s）分解為：

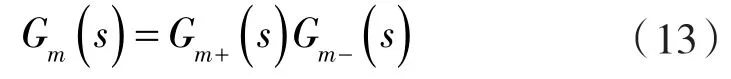
其中，Gm+（s）為模型中的純滯后環(huán)節(jié)和非最小相位部分，Gm?（s）為模型中的最小相位部分。然后在最小相位部分1/Gm?（s）增加濾波器保證系統(tǒng)的穩(wěn)定性和魯棒性，定義內(nèi)模控制器為：

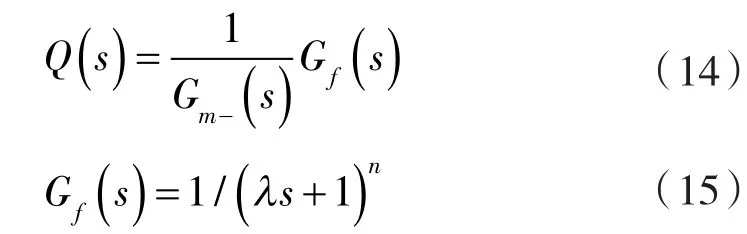
濾波器Gf（s）通常選用如上形式。其中λ為唯一需要調(diào)節(jié)的濾波器參數(shù)，λ的選取影響著系統(tǒng)的閉環(huán)相應(yīng)速度和系統(tǒng)穩(wěn)定性。λ越小系統(tǒng)的閉環(huán)響應(yīng)速度越快，但穩(wěn)定性降低；λ越大系統(tǒng)的穩(wěn)定性越高，但閉環(huán)響應(yīng)速度變差。n為濾波器階次，為了實(shí)現(xiàn)傳遞函數(shù)的嚴(yán)格正則性，n需要與系統(tǒng)的階次保持一致。

由式（6）、（13）和（14）可以得到圖 4 結(jié)構(gòu)所示的控制器表達(dá)式：

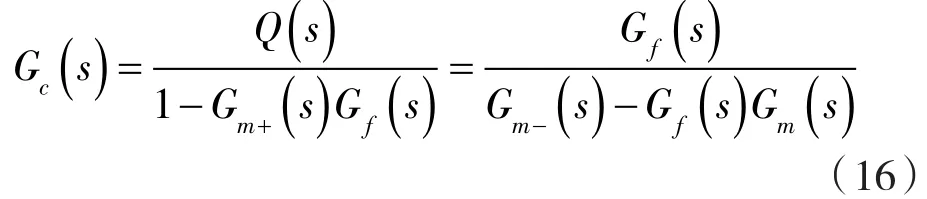
到此一個(gè)常規(guī)的內(nèi)模控制器已經(jīng)初步搭建完成。通過(guò)對(duì)控制器Gc（s）進(jìn)行數(shù)學(xué)變換變成PID控制器的形式，將內(nèi)模控制與PID控制結(jié)合構(gòu)成內(nèi)模PID控制器。

同大多數(shù)穩(wěn)定過(guò)程一樣，往復(fù)壓縮機(jī)氣量調(diào)節(jié)系統(tǒng)也能用簡(jiǎn)單的一階純滯后模型來(lái)表示，其數(shù)學(xué)模型形式為：

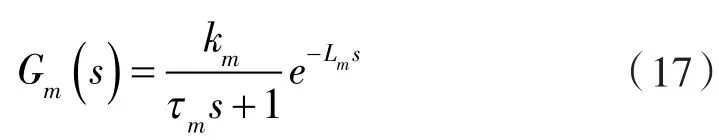
式中參數(shù)km，τm，Lm分別表示過(guò)程增益、時(shí)間常數(shù)和時(shí)滯時(shí)間。

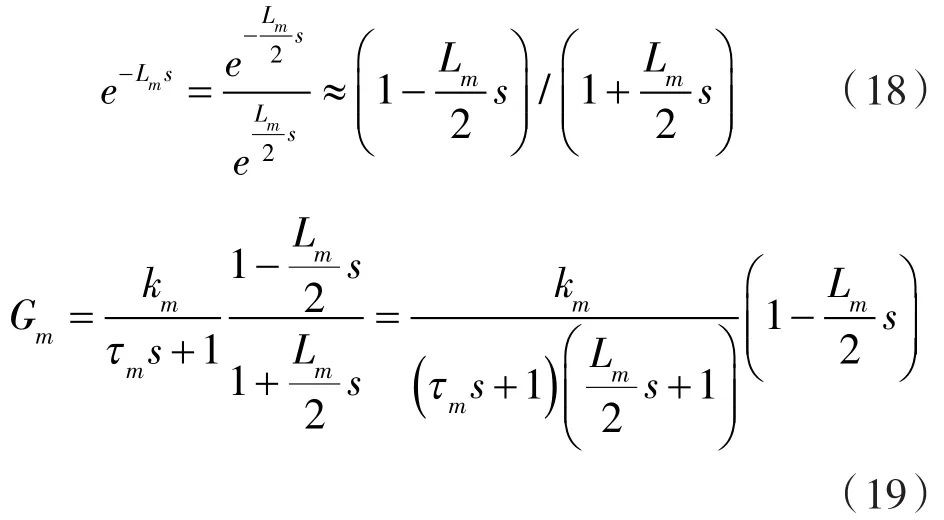
濾波器階數(shù)n與系統(tǒng)階數(shù)保持一致，即n=1。于是適用一階純滯后系統(tǒng)的內(nèi)模控制器和具有反饋形式的控制器可以表示為：

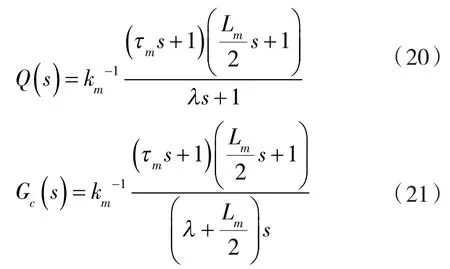
若PID控制器取下式結(jié)構(gòu)形式：

其中，KP，Ki和Kd分別為比例、積分和微分常數(shù)。

再將式（22）進(jìn)行數(shù)學(xué)變換得到具有PID控制器結(jié)構(gòu)形式表達(dá)式：

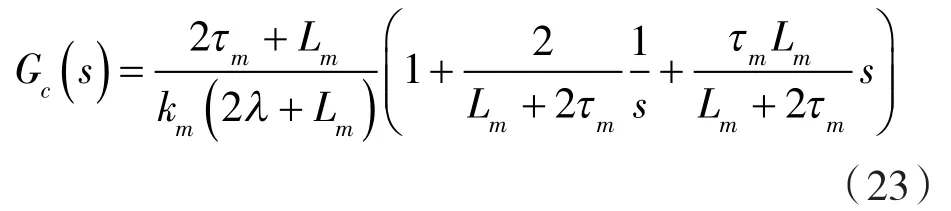
然后可以得到PID控制器的各項(xiàng)參數(shù)：

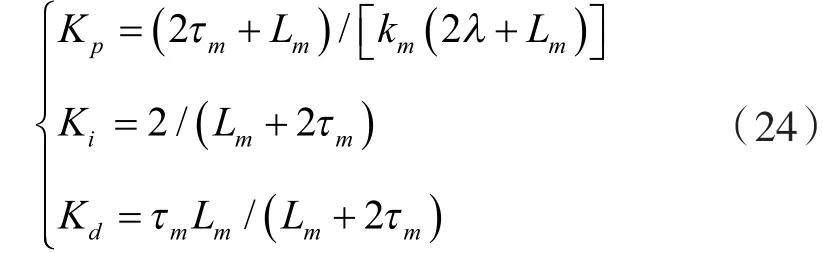
可以看出，控制器僅含有一個(gè)可調(diào)參數(shù)λ，該參數(shù)的選取直接影響到系統(tǒng)的動(dòng)態(tài)性能和魯棒性。

解耦控制是通過(guò)設(shè)計(jì)解耦補(bǔ)償器，將一個(gè)具有耦合特性的多輸入多輸出的系統(tǒng)解耦成多個(gè)獨(dú)立的單輸入單輸出系統(tǒng)。前饋補(bǔ)償解耦是多變量解耦控制中最早使用的一種解耦方法，該方法結(jié)構(gòu)簡(jiǎn)單且易于實(shí)現(xiàn)，因此得到廣泛的應(yīng)用。圖5表示一個(gè)二輸入二輸出系統(tǒng)的前饋補(bǔ)償解耦控制結(jié)構(gòu)。

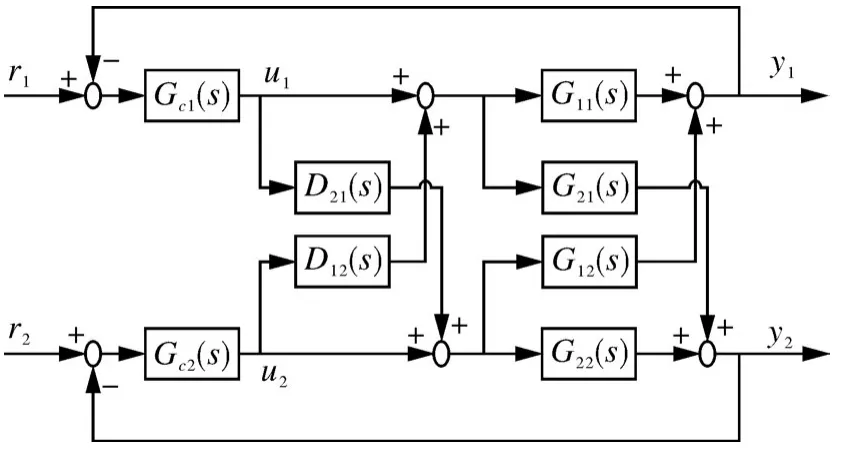
圖5 前饋補(bǔ)償解耦控制框Fig.5 Block diagram of feedforward compensation decoupling control

若要實(shí)現(xiàn)對(duì)r1與r2、y1與y2之間的解耦，根據(jù)前饋補(bǔ)償原理可得：

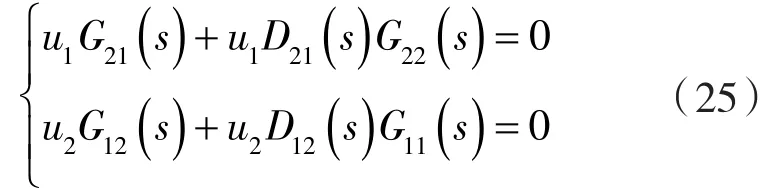
由此解得前饋補(bǔ)償解耦器的傳遞函數(shù)［12］為：

3 數(shù)值仿真

為驗(yàn)證本研究方法的有效性，以二級(jí)往復(fù)壓縮機(jī)氣量調(diào)節(jié)系統(tǒng)為研究對(duì)象，用MATLAB工具進(jìn)行仿真研究，由第2節(jié)得到的氣量調(diào)節(jié)系統(tǒng)的傳遞函數(shù)模型：

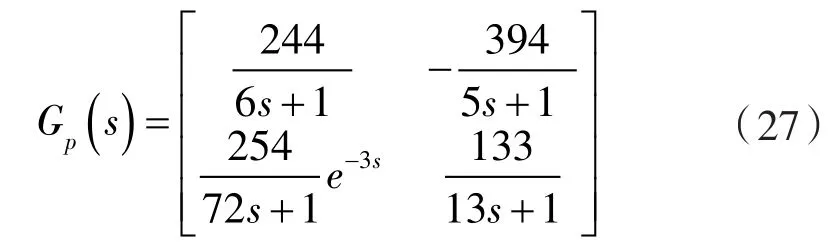
若模型能夠精確地描述受控過(guò)程，則有Gp（s）=Gm（s）。在此模型基礎(chǔ)上按照第 3 節(jié)所述方法進(jìn)行內(nèi)模PID設(shè)計(jì)：

步驟1：前饋補(bǔ)償解耦器設(shè)計(jì)。

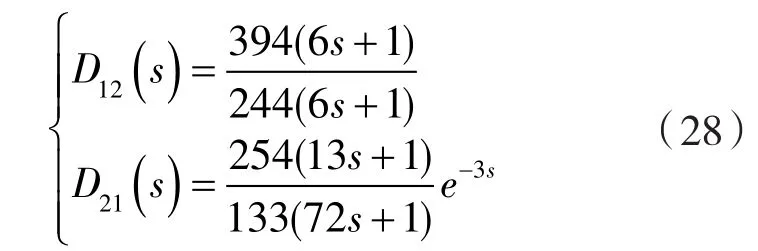
步驟2：內(nèi)模 PID 控制器設(shè)計(jì)。

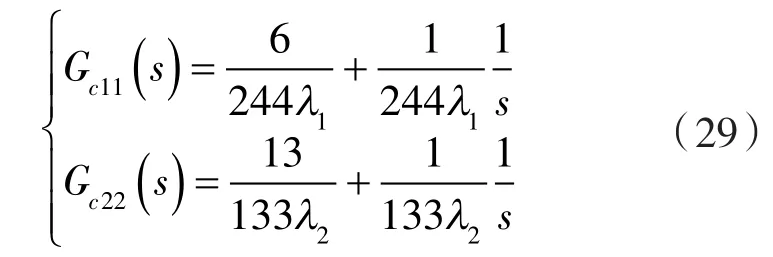
仿照往復(fù)式壓縮機(jī)氣量調(diào)節(jié)系統(tǒng)常規(guī)的啟動(dòng)流程，系統(tǒng)將從機(jī)組停機(jī)狀態(tài)下啟動(dòng)，在各級(jí)排氣壓力穩(wěn)定后再投用氣量調(diào)節(jié)系統(tǒng)。將一級(jí)排氣壓力初始值設(shè)定為120 kPa，二級(jí)排氣壓力初始值設(shè)定為220 kPa。根據(jù)圖5控制結(jié)構(gòu)對(duì)模型進(jìn)行仿真研究，由式（24）可得IMC-PID的各項(xiàng)參數(shù)見(jiàn)表1。

表1 IMC-PID控制器參數(shù)Tab.1 IMC-PID controller parameters

用上述控制器參數(shù)對(duì)各級(jí)壓力進(jìn)行階躍響應(yīng)測(cè)試及抗干擾測(cè)試，并和常規(guī)的PID控制方法進(jìn)行對(duì)比。通過(guò)經(jīng)驗(yàn)法得出的常規(guī)PID控制器最優(yōu)參數(shù)見(jiàn)表2。

表2 常規(guī)PID控制器參數(shù)Tab.2 Conventional PID controller parameters

3.1 排氣壓力階躍響應(yīng)測(cè)試

投用氣量調(diào)節(jié)系統(tǒng)，在機(jī)組各級(jí)工作負(fù)荷及排氣壓力均處于穩(wěn)定狀態(tài)后，依次改變一級(jí)和二級(jí)排氣壓力的設(shè)定值，對(duì)系統(tǒng)進(jìn)行階躍響應(yīng)測(cè)試。對(duì)比系統(tǒng)在前饋解耦補(bǔ)償內(nèi)模PID控制下和常規(guī)PID控制下的控制效果。

第1步：改變一級(jí)排氣壓力設(shè)定值，由圖6可以看出，在內(nèi)模解耦PID控制作用下，一級(jí)排氣壓力能迅速達(dá)到設(shè)定值且無(wú)超調(diào)量，控制系統(tǒng)具備較好的調(diào)節(jié)快速性。而且二級(jí)排氣壓力處于穩(wěn)定狀態(tài)，一級(jí)排氣壓力的改變沒(méi)有對(duì)二級(jí)排氣壓力造成干擾，系統(tǒng)具備較好的解耦性。相比較地，系統(tǒng)在常規(guī)PID控制下，一級(jí)排氣壓力產(chǎn)生2%的超調(diào)量，調(diào)節(jié)時(shí)間較長(zhǎng)；一級(jí)排氣壓力的改變會(huì)對(duì)二級(jí)排氣壓力產(chǎn)生影響，系統(tǒng)未完全解耦。

圖6 一級(jí)階躍響應(yīng)曲線(xiàn)Fig.6 First order step response curve

第2步：改變二級(jí)排氣壓力設(shè)定值。由圖7可以看出，相比較常規(guī)PID控制策略，系統(tǒng)在前饋解耦補(bǔ)償內(nèi)模PID控制作用下調(diào)節(jié)速度更為快速，主控變量二級(jí)排氣壓力迅速達(dá)到設(shè)定值且無(wú)超調(diào)量，對(duì)一級(jí)排氣壓力無(wú)耦合干擾。而系統(tǒng)在常規(guī)PID控制作用下調(diào)節(jié)時(shí)間更長(zhǎng)且一級(jí)排氣壓力產(chǎn)生了波動(dòng)。可見(jiàn)內(nèi)模解耦PID控制比常規(guī)PID控制具有更好的快速性與穩(wěn)定性。

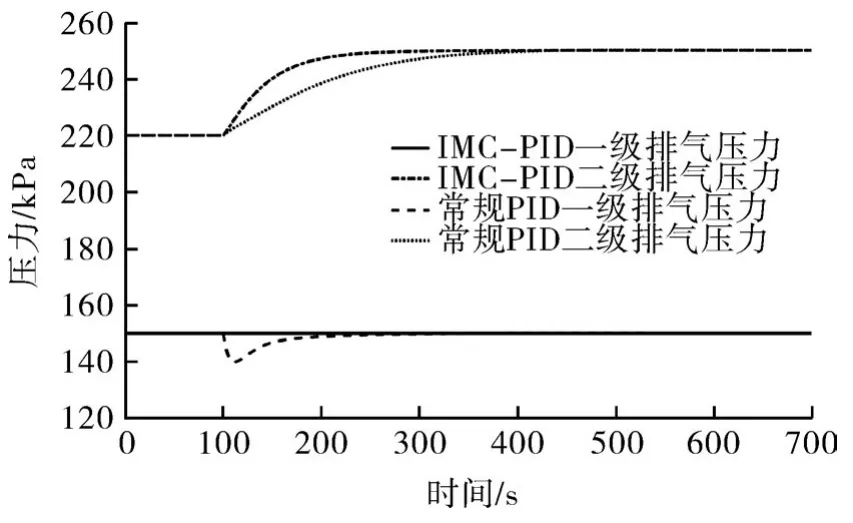
圖7 二級(jí)階躍響應(yīng)曲線(xiàn)Fig.7 Second order step response curve

兩種控制方法的時(shí)域性能指標(biāo)對(duì)比見(jiàn)表3。可以看出內(nèi)模解耦PID控制方法的各項(xiàng)指標(biāo)都優(yōu)于常規(guī)PID控制。

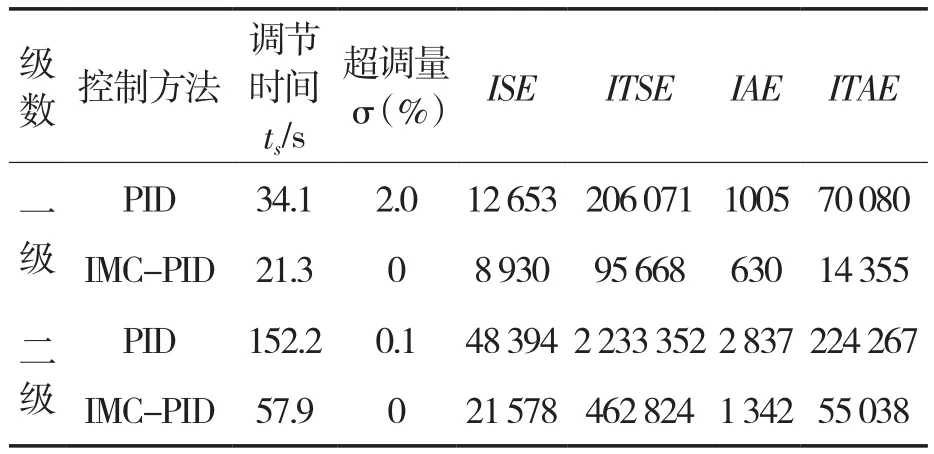
表3 時(shí)域性能指標(biāo)分析Tab.3 Time domain performance index analysis

3.2 排氣壓力魯棒性測(cè)試

在機(jī)組工作負(fù)荷與排氣壓力都處于穩(wěn)定狀態(tài)下，模擬排氣緩沖罐壓力突變的情況，分別給一級(jí)排氣壓力和二級(jí)排氣壓力施加一個(gè)20 kPa的階躍信號(hào)。

第1步：在二級(jí)排氣壓力設(shè)定值保持不變的情況下給一級(jí)排氣壓力施加20 kPa的階躍信號(hào)。由圖8可以看出，在內(nèi)模解耦PID控制作用下，一級(jí)排氣壓力在干擾作用過(guò)后能迅速平穩(wěn)地回歸設(shè)定值，且二級(jí)排氣壓力無(wú)波動(dòng)產(chǎn)生。相對(duì)地，系統(tǒng)在常規(guī)PID控制作用下的自動(dòng)調(diào)節(jié)能力較弱，且無(wú)法消除對(duì)其他控制變量的耦合作用。

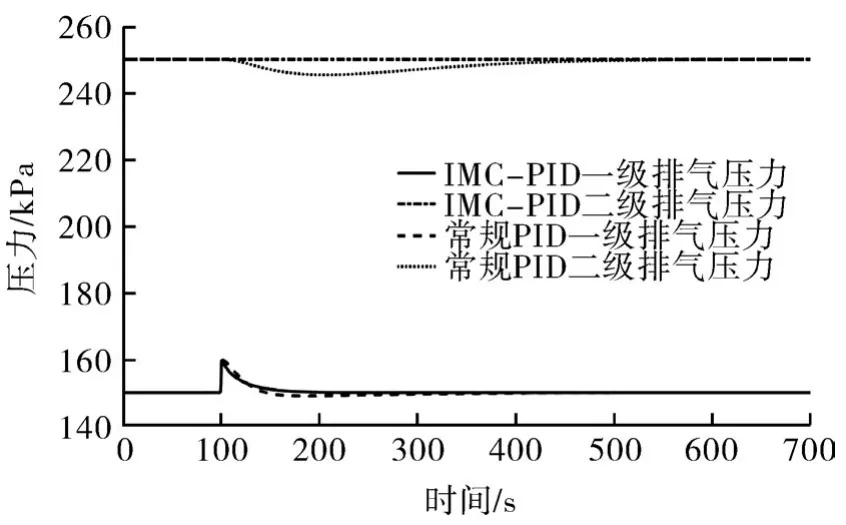
圖8 一級(jí)魯棒性測(cè)試曲線(xiàn)Fig.8 First order robustness test curve

第2步：接下來(lái)在一級(jí)排氣壓力不變的情況下給二級(jí)排氣壓力施加20 kPa的階躍信號(hào)。由圖9可以看出，和一級(jí)排氣壓力抗干擾測(cè)試結(jié)果類(lèi)似，系統(tǒng)在內(nèi)模解耦PID控制作用下，二級(jí)排氣壓力迅速回歸設(shè)定值，一級(jí)排氣壓力無(wú)波動(dòng)產(chǎn)生。而常規(guī)PID控制器則出現(xiàn)了調(diào)節(jié)速度慢、耦合等情況。

圖9 二級(jí)魯棒性測(cè)試曲線(xiàn)Fig.9 Second order robustness test curve

4 結(jié)論

針對(duì)往復(fù)式壓縮機(jī)氣量調(diào)節(jié)系統(tǒng)多變量、強(qiáng)耦合等特點(diǎn)，本文探索了一種有效的內(nèi)模解耦PID 控制器。相較其他控制方法，該方法具有以下優(yōu)勢(shì)：

（1）具有更優(yōu)的設(shè)定值跟蹤性能，快速達(dá)到系統(tǒng)的設(shè)定值且無(wú)超調(diào)量產(chǎn)生；

（2）具有更強(qiáng)的魯棒性，在壓力產(chǎn)生波動(dòng)后，系統(tǒng)能快速調(diào)節(jié)干擾所在回路的壓力值，保證系統(tǒng)平穩(wěn)地運(yùn)行；

（3）具有較好的解耦性，將原先的耦合系統(tǒng)分解為多個(gè)獨(dú)立的子系統(tǒng)，便于調(diào)控。