基于模擬退火模型運輸路徑網優化研究

莊夢婷

安徽財經大學統計與應用數學學院，中國·安徽 蚌埠 233030

1 引言

同城配送存在路徑迂回問題，所謂迂回運輸就是沒有從最短的路線運輸，而是繞道運輸的形式，如因到達地區順序不同而導致的總路徑變長。物流公司不能以最近的公路運輸，將會直接影響公司的運輸效率降低，也會導致不必要的運輸成本增加[1]。而道路迂回問題是在很多物流配送過程中存在的問題。

配送車輛承載量的約束條件：每輛貨車都存在其重量承載量以及體積承載量，考慮到承載量的問題，每輛貨車所承載的貨物有限。綜合考慮不同城區物流件數之間存在的差異，派送車輛數量成為一個問題。時間約束因素包括即物流配送過程貨物有要求到達時間、大部分同城運輸都要求在當天完成貨物配送，其他因素包括路段時速限制、堵車的可能性、天氣限速。

2 研究設計

2.1 基于模擬退火模型的單式運輸路徑優化

針對起點到終點只有一種運輸方式可供選擇，即直達的情況，我們擬建立模擬退火模型從運輸路徑角度進行優化；綜合考慮車的承載量以及不同地區訂單數存在的差異的問題，利用聚類分析，將地區進行分類，在不同地區上利用模擬退火算法進行不同區域的最短路徑計算。具體包括：發貨點和收貨點的設置；規劃適當的路線；使運輸車輛能夠有序地通過計劃中的地點以及完成貨物的需求量和發貨量，并且滿足交貨時間，即達到實現最短時間內；最短運輸成本下完成相應的目標，去掉在路上的“浪費”[2]。

2.2 研究方法：模擬退火算法

模擬退火是一種通用概率算法，用來在一個大的搜尋空間內找尋命題的最優解。其來源于固體退火原理，將固體加溫至充分高，再讓其徐徐冷卻。加溫時，固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最后在常溫時達到基態，內能減為最小[3]。對于地點之間的轉移概率矩陣兩兩相互之間是互通的，即可得出該轉移矩陣對應的有限的馬爾科夫鏈是收斂的。收斂說明過程將達到平衡狀態，即此后過程取某一個狀態的概率不隨時間變化[4]。

①解空間S表示為{2,3, ,}n,1 … 的所有起點和終點的循環排列集合，即：

其中，每一個循環排列表示運輸完n個運輸點的一個回路，πi=m 表示在第i-1次運輸目標m，初始解可選為(1 , 2,3,…, n)，這里使用蒙特卡洛法求得一個比較好的初始解。

②目標函數：目標函數為一次走過所有運輸點的路徑長度，即：

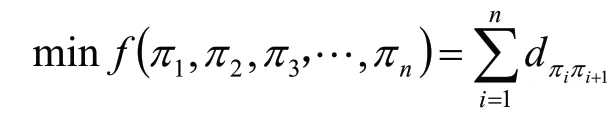
③新解的產生。設上一步迭代的解為：

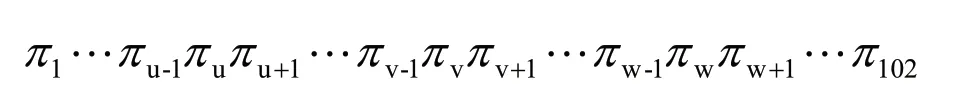
應用變換法時，任選序號u,v交換u和v之間的順序，變成逆序，此時的新路徑為：

④代價函數差：對于2變換法，路徑差可表示為：

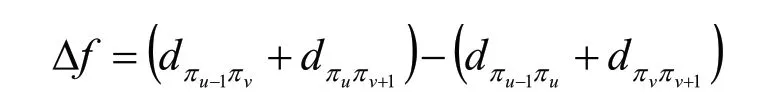
⑤接受準則：

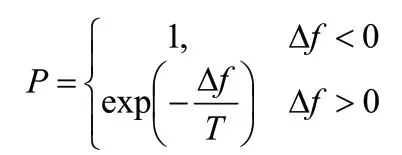
⑥降溫：利用選定的降溫系數α進行降溫，取新的溫度T為αT（這里T為上一步迭代的溫度），這里選定α = 0.999。

⑦結束條件：用選定的終止溫度e = 10-30，判斷退火過 程是否結束。若T＜e，則算法結束，輸出當前狀態[5]。

求解過程如模擬退火流程圖1所示。

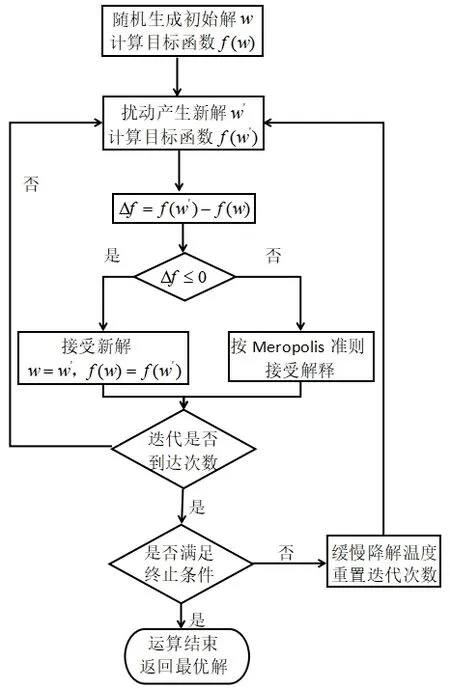
圖1 模擬退火流程圖

2.3 數據的搜集和處理

由案例以及網上搜索可得到中國北京市某次單運輸方式任務的物流采購點以及產品運輸點，并將中國北京市需要運輸的運輸點以坐標點的形式寫在一個平面上。

根據上述流程圖，我們為空間設計了LINGO自動診斷的代碼，只要將某次需要向外運輸或者采購原材料的運輸點坐標數據輸入并在程序中加入循環語句，運行出運行結果，得到最短運輸路徑。這條運輸路徑能保證運輸人員在無一運輸點遺漏的情況下，所走的運輸路徑最短，也就是說此時達到了路徑的優化。

3 算例分析

為了更好地體現模擬退火模型在單一運輸方式上的運輸效果，我們以中國北京市某次運輸案例為例，運用模擬退火模型對路徑進行優化設計。選取中國北京市為例，提貨區為朝陽區，剩余地區為所需配送地區。

距離矩陣如下表1所示。

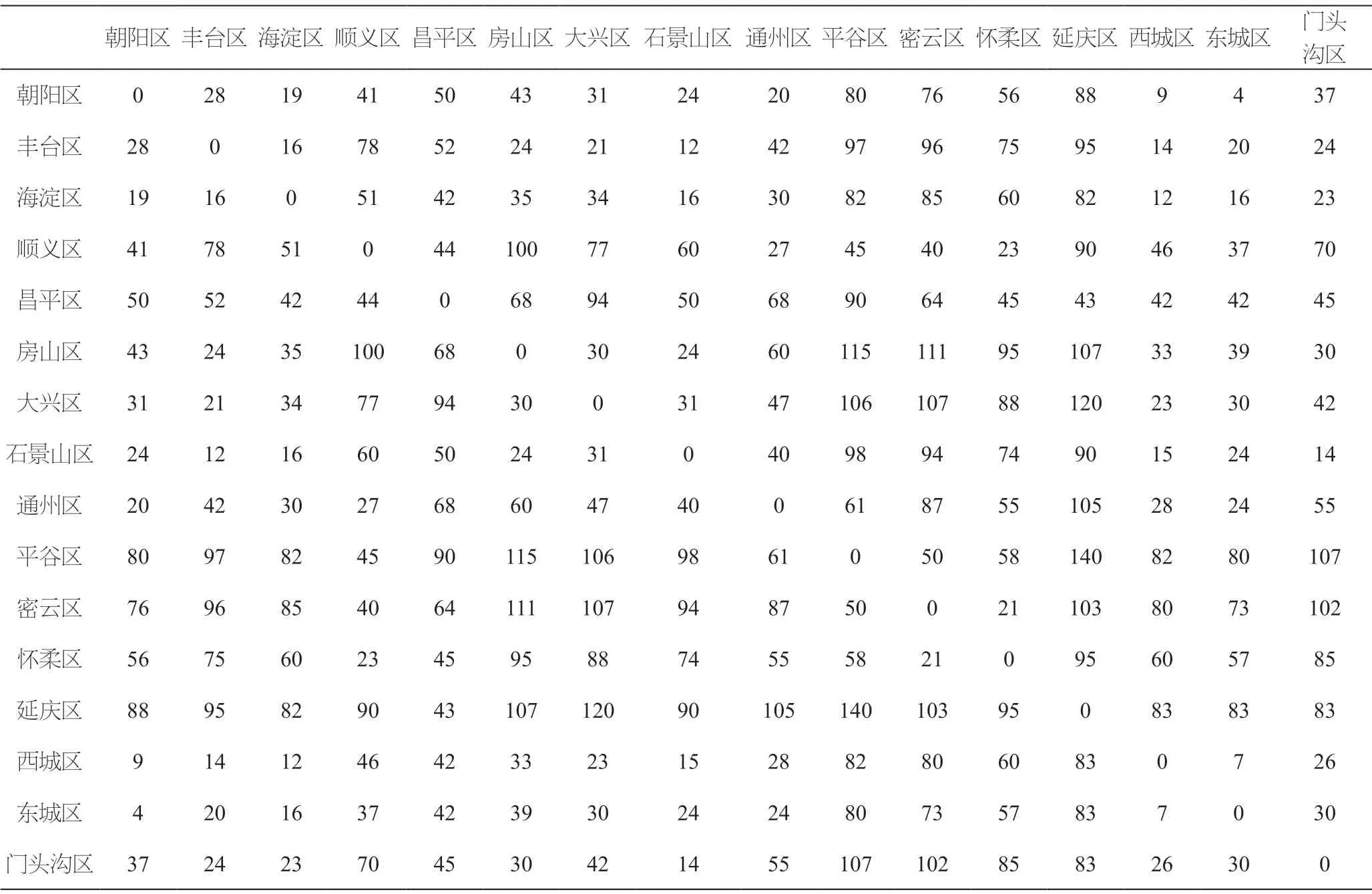
表1 北京市各區距離矩陣

3.1 單一式配送

在不考慮訂單量的約束條件下，貨物從起點出發，送達各目的地對應的編號如表2所示[6]。

表2 地區編號

目標函數為尋找從點出發，遍歷中間點，返回n的最短路徑。在計算機上運行以上程序，總運輸距離為462km，運輸路徑為1-15-14-3-2-7-6-8-16-13-5-12-11-10-4-9，表明從朝陽區出發，經過東城區、西城區、海淀區、豐臺區、大興區、房山區、石景山區、門頭溝區、延慶區、昌平區、懷柔區、密云區、平谷區、順義區，最終回到通州區。

3.2 多車配送

考慮到訂單量的情況下，將中國北京市16各地區首先要根據地理位置進行分類，再結合訂單多、少相互配合，聚類圖如下圖2所示[7]。

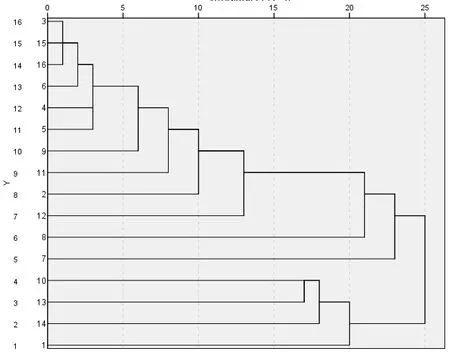
圖2 聚類結果圖

將地區分為三類：

第一類為順義區、平谷區、密云區、柔懷區、昌平區、延慶區，這些地區中，順義區訂單最多，其余地區訂單較少，恰好滿足貨車的承載量需求。

第二類為在滿足貨車承載量的前提下訂單量較多的通州區和大興區。

第三類為東城區，西城區、海淀區訂單較多和門頭溝區和房山區訂單較少的地區組成。重復上述計算過程，得出每個區的最短路徑和總路徑。

結果顯示，第一類的路徑為朝陽區、順義區、平谷區、密云區、柔懷區、昌平區、延慶區，最終回到朝陽區，路徑長度為333km。第二類路徑為從朝陽區出發，先結果通州區，再到大興區，最后回到朝陽區，路徑長度為98km。第三類路徑為朝陽區、東城區、海淀區、石景山區、門頭溝區、房山區、豐臺區、西城區，最后回到朝陽區，該路徑長度為127km。三類區域總路徑為558km。

4 結語

由算例分析，我們可以發現模擬退火算法的優點和在應用中進行推廣的原因：

①在用模擬退火模型處理最短路徑問題的時候，編程工作量少，且易于實現，統計上可以保證找到全局最優解。

②模擬退火算法是一種新的隨機搜索方法，適合于解決大規模組合優化問題的通用而有效的近似算法。因此，也適用于論文中的運輸優化問題。

③與以往的近似算法相比,模擬退火算法具有描述簡單、使用靈活、運用廣泛、運行效率高和較少受到初始條件約束等優點。

④模擬退火在找到最優解時需要花費非常多的時間，當冷卻速度過快時，會導致模擬退火無法找到最優解，但速度過慢，又會導致運行時間變長。

此模型可以對各類運輸問題的路徑進行優化，只要將運輸點數量輸入程序和將運輸點變換為坐標格式，就能得到一次性走過各點的最短路徑，避免了重復走在運輸上的“浪費”，這也是基于節能減排理念的一種物流優化。利用此方法，可以將很多交通以及其他方面的交通運輸問題達到路徑最優化，從而實現高效的交通運輸速度。