R513A的飽和液相黏度特性研究

陳裕博，楊昭，武曉昆，呂子建，張勇

（1 天津大學中低溫熱能高效利用教育部重點實驗室，天津300350；2 空調設備及系統運行節能國家重點實驗室，廣東珠海519070）

引 言

近年來，隨著HCFCs、HFCs的消耗量飛速增長，人們逐漸認識到了它們對全球變暖產生的影響。在Hawken 列出的80 項緩解全球變暖的戰略中,制冷劑管理排在了第一位[1]。在蒙特利爾議定書的第28次締約方大會中，197個締約方達成了《基加利修正案》[2]，將18 種高GWP 的HFCs 納入監控目錄，并給出了各國淘汰HFCs 的時間表。為了緩解傳統制冷劑的溫室效應，尋找低GWP且高效的新型制冷劑已成為制冷行業的一項重要任務。

R513A（R1234yf/R134a，56/44）是一種零ODP、低GWP 的混合制冷劑，可作為R134a 的替代制冷劑。Mota-Babiloni 等[3]比較了R513A 和R134a 在蒸氣壓縮式系統中運行性能的差異，實驗中R513A 的質量流量高于R134a，這使得R513A 的制冷量和COP 皆優于R134a。張治平等[4]對比分析了R134a和R513A 在離心式冷水機組中的熱力循環性能，結果表明，在相同工況下，R513A 的制冷量和性能系數略低于R134a。上述兩篇文獻的循環測試結果相反，這是因為當兩種工質的體積流量相近時，由于R513A 的蒸氣密度更高，所以其質量流量更高。而在相似的過冷和運行條件下，R513A 的制冷效果要低于R134a，功耗要大于R134a。考慮到不同的機組，兩種工質制冷量和COP 值的相對大小分別取決于質量流量與制冷效果（蒸發器焓差）的差異，制冷量與功耗的差異。此外，科慕公司[5]公布了R513A油溶性、材料兼容性、熱物理性質的相關數據，但熱物性參數皆基于REFPROP 10.0 進行理論預測。由此可見，目前R513A 的研究主要集中于系統循環性能[6-9]和流動傳熱[10-11]方面，有必要進一步研究其熱物理性質。

黏度是流體重要的遷移性質，對流動中的傳熱和壓降特性會產生重要影響。在制冷系統的設計計算和優化過程中都需要黏度數據，制冷劑黏度在研究循環性能參數時具有重要意義。在混合制冷劑R513A 的推廣應用過程中，首先要探明其黏度特性。目前國內外學者采用多種方法進行了制冷劑液相黏度實驗研究。Han 等[12-13]設計了一種改進型Ubblohde 黏度計，在溫度范圍233.15～333.15 K 內測量了R32 和R134a 的飽和液相黏度。劉志剛等[14]在上述黏度計的基礎上添加了旁通管，有效地避免了毛細管液柱高度的修正問題，提高了實驗數據的精度。吳江濤等[15-17]采用該黏度計測得了R152a、DME、甲基叔丁醚、甲醇與蓖麻油混合物的飽和液相黏度。袁曉蓉[18]研制了一套適用于測量混合制冷劑液相黏度的旋轉式毛細管黏度計，在溫度范圍278.15～333.15 K測量了R1234yf/R134a、R1234yf/R152a、R134a/R152a 的飽和液相黏度。許晨怡等[19]采用毛細管法測量了R1336mzz(E)的液相黏度。Meng 等[20-23]采用振動弦法測量了R32、R245fa、R1234yf、R1234ze(E)、R1233zd(E)和R32/R1234yf 的液相黏度。Bair 等[24]通過落球式黏度計測量了R32和R410A 的液相黏度，最高壓力可達350 MPa。Cui等[25-26]采用表面光散射法測量了純制冷劑R1233zd(E)和混合制冷劑R32/R1234yf、R32/R1234ze(E)的飽和液相黏度，并采用多項式方程與液相黏度數據進行關聯。Dang 等[27]使用移動活塞式黏度計測量了混合制冷劑R32/R1234yf、R125/R1234yf 的液相黏度，并采用硬球模型與實驗數據進行關聯。

目前，國內外學者開展了大量的制冷劑替代工作。為了推廣新一代制冷劑R513A 的應用，本文開展了R513A 的飽和液相黏度實驗研究，采用R-K 多項式方程以及硬球模型結合混合規則預測R513A的飽和液相黏度，對兩個模型的誤差進行分析，以期為R513A的替代應用研究提供參考依據。

1 實驗材料和方法

1.1 材料

實驗所用制冷劑R513A（R1234yf/R134a，56/44）由科慕公司提供，其質量分數大于99.9%，具體物性參數見表1。

表1 制冷劑基本物性參數Table 1 Basic physical properties of refrigerant

1.2 飽和液相黏度測試裝置

常見的流體黏度測量方法主要包括毛細管法、振動法、旋轉法、落球法、表面光散射法，其中毛細管黏度計因其結構簡單、精度較高而得到了廣泛的應用。因此本文基于毛細管法[28]，并根據實驗需求，設計搭建了一套制冷劑飽和液相黏度測試系統。黏度測試系統主要包括雙層反應釜、毛細管黏度計、升降翻轉機構、高精度恒溫槽、配氣及真空系統、控制及數據采集系統，如圖1所示。

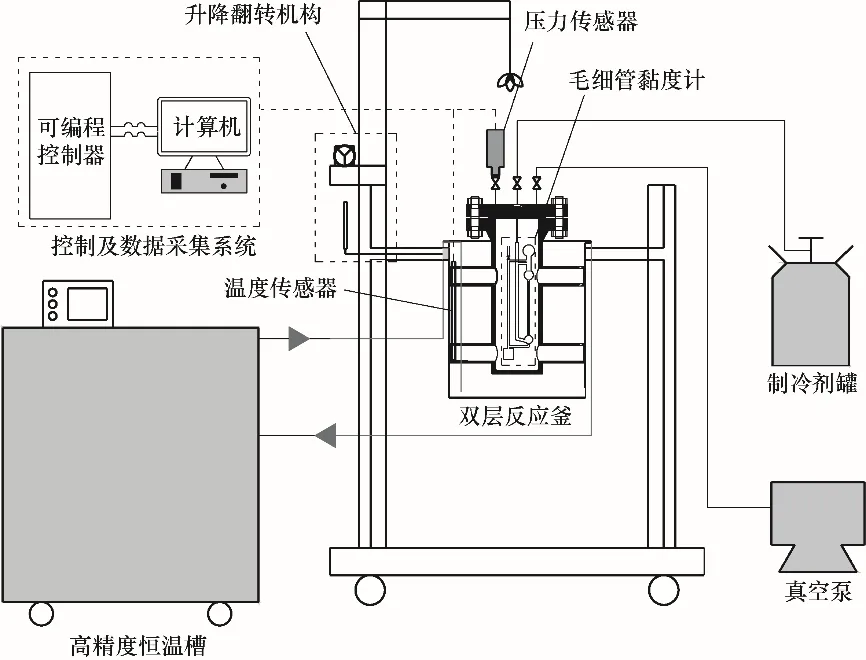
圖1 黏度測試系統示意圖Fig.1 The schematic diagram of viscosity test system

毛細管黏度計主要包括上貯液器、計時球、毛細管、緩沖球、升液管、下貯液器，黏度計的緩沖球上接有注液管，上貯液器與計時球之間設有與注液管相通的旁通管。其中毛細管的內徑為0.31 mm，長度為140 mm，計時球的體積約為7000 mm3,上、下貯液器的體積約為14000 mm3。

實驗所用恒溫槽的溫度調節范圍為233.15～423.15 K，溫度不確定度≤0.01 K/30 min，溫度均勻度≤0.01 K，采用外循環連接方式，循環流量為15～16 L·min-1。反應裝置由雙層反應釜和毛細管黏度計構成，雙層反應釜可分內、外兩層，外層與恒溫槽相連，為內層壓力容器提供穩定的恒溫環境。壓力容器的設計壓力為7 MPa，用以放置毛細管黏度計，為保證良好的視覺觀察效果，壓力容器左右兩側安裝有觀察窗。通過升降翻轉機構帶動壓力容器翻轉，以完成升液過程。實驗過程中，采用高精度的鉑電阻溫度計（±0.1 K）和壓力傳感器（量程0～4 MPa，精度±0.5%FS）分別進行溫度和壓力的測量。

1.3 黏度計常數標定

由式（1）可知，在測量制冷劑液相黏度之前，必須利用標準液體對毛細管黏度計的儀器常數A和B進行標定。對于同一根毛細管黏度計，其幾何尺寸是固定的，因此毛細管黏度計常數為定值。本文選用黏度數據豐富的R134a 作為標準液體，通過測量R134a 流經毛細管黏度計計時球的時間和其溫度值，由NIST REFPROP 9.1[29]查詢得到對應溫度下的飽和液相黏度值和飽和氣液相密度值，進而回歸計算得到黏度計常數A和B。R134a 的實驗測量值見表2。

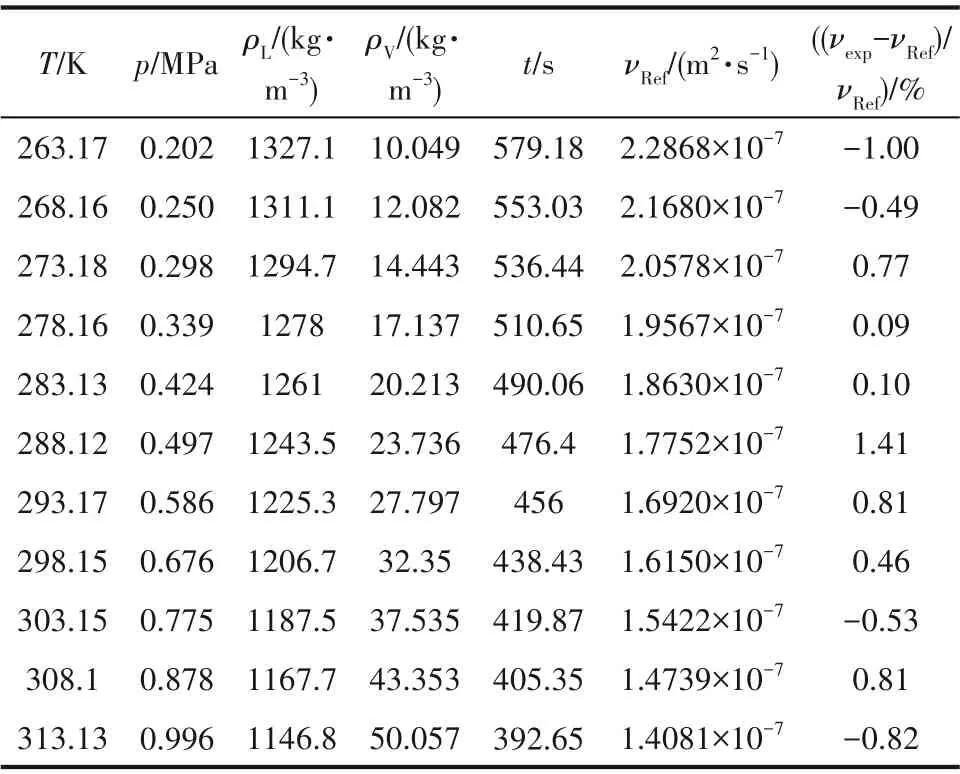
表2 R134a的實驗測量值及標準運動黏度Table 2 Experimental data and standard kinematic viscosity of R134a

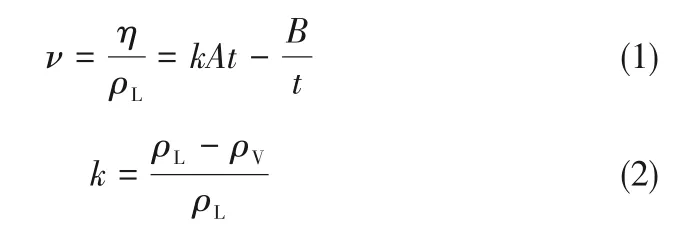
式中，ν為運動黏度，mm2·s-1；η為動力黏度，μPa·s；ρL、ρV分別為飽和液相密度和氣相密度，kg·m-3；t為流體流動時間，s。

在溫度范圍263.15～313.15 K 內，測量了R134a流經黏度計計時球的時間，需保證同一溫度下5 次測量時間的最大偏差在2 s以內，取實驗數據的平均值最終用于標定黏度計常數，得到A=4.1136×10-10，B=5.817×10-6。實驗值νexp與標準值νRef的偏差分布如圖2 所示，兩者平均絕對偏差為0.66%，最大絕對偏差為1.41%。

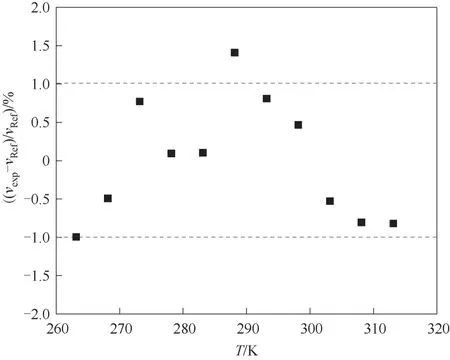
圖2 R134a黏度實驗值與標準值的偏差分布Fig.2 Deviation between experimental and standard viscosity of R134a

1.4 實驗不確定度分析

為了準確地評估實驗系統測試結果的可靠性，需要對實驗系統進行不確定度分析。本實驗測量的主要物理量是溫度、壓力、時間，其中溫度測量值的不確定度主要來源于溫度傳感器和恒溫槽；壓力測量值的不確定度主要來源于壓力傳感器；黏度測量值的不確定度主要來源于時間。溫度和壓力測量的擴展不確定度由式（3）得到：

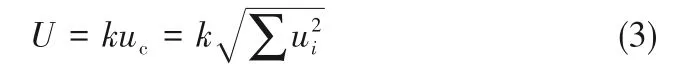
式中，ui為各個因素的相對標準不確定度；uc為合成標準不確定度；k為置信因子，取置信概率為95%，k取值為2。

在實驗過程中，二級標準鉑電阻溫度傳感器的測量不確定度小于±0.01 K，Pt100 溫度傳感器的測量不確定度小于±0.1 K，恒溫槽的波動度與均勻度小于0.01 K/30 min。壓力傳感器的量程為0～4 MPa，精度為±0.5%FS，測量不確定小于20000 Pa。綜上所述，溫度和壓力測量的擴展不確定度分別為±0.2 K、±40000 Pa。

對于時間的測量，其誤差主要源于人為操作。本文以同一溫度下5次測量時間的平均值作為流體流動時間。在實驗過程中，測量時間的最大絕對偏差為±2.0 s，最短的流動時間為329.5 s，液相黏度的測量不確定度為：

由于末端修正項B/t在運動黏度的測試結果中所占比例很小，一般不考慮它的作用，因此運動黏度的測量不確定度與時間的測量不確定度相當，即工質運動黏度的測量不確定度為0.61%。

2 實驗結果與討論

2.1 R513A飽和液相黏度測試

實驗測量了共沸制冷劑R513A 的飽和液相黏度，測試溫度范圍為253.15～333.15 K。在測試溫度點下，待壓力穩定達到制冷劑飽和狀態，開始進行液相黏度測試，其中飽和氣液相密度從NIST REFPROP 9.1[29]中查詢得到，每個溫度點至少進行5次測量以減小實驗的測量誤差，最終取其平均值作為測試結果。實驗結果表明，R513A 的飽和液相黏度略低于R134a，結果如表3和圖3所示。

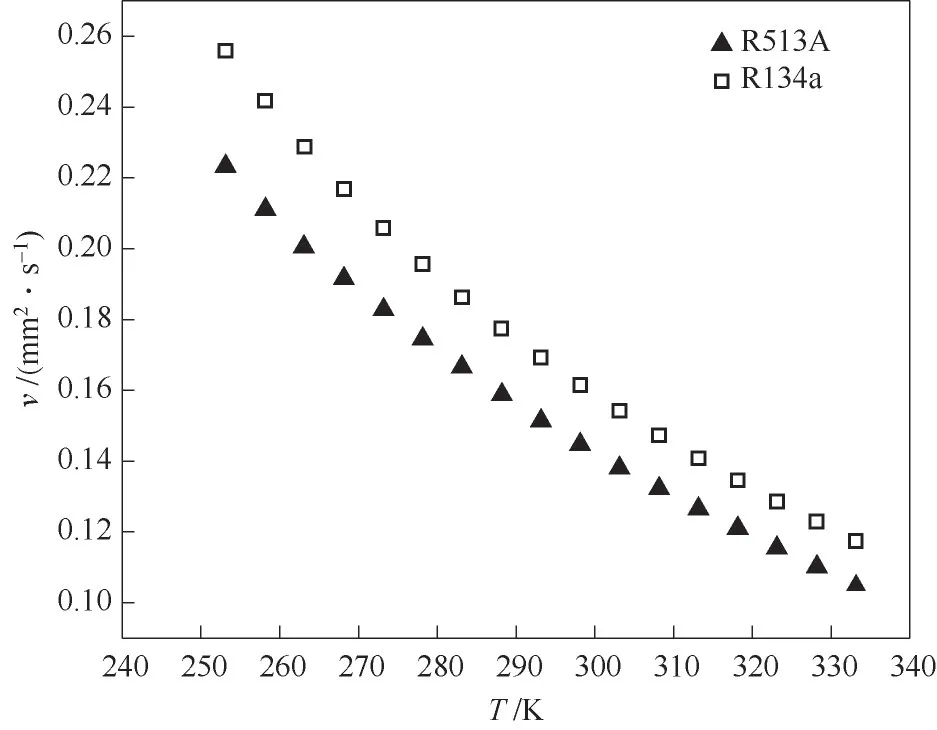
圖3 R513A飽和液相黏度值隨溫度的變化Fig.3 R513A saturated liquid viscosity varied with temperature

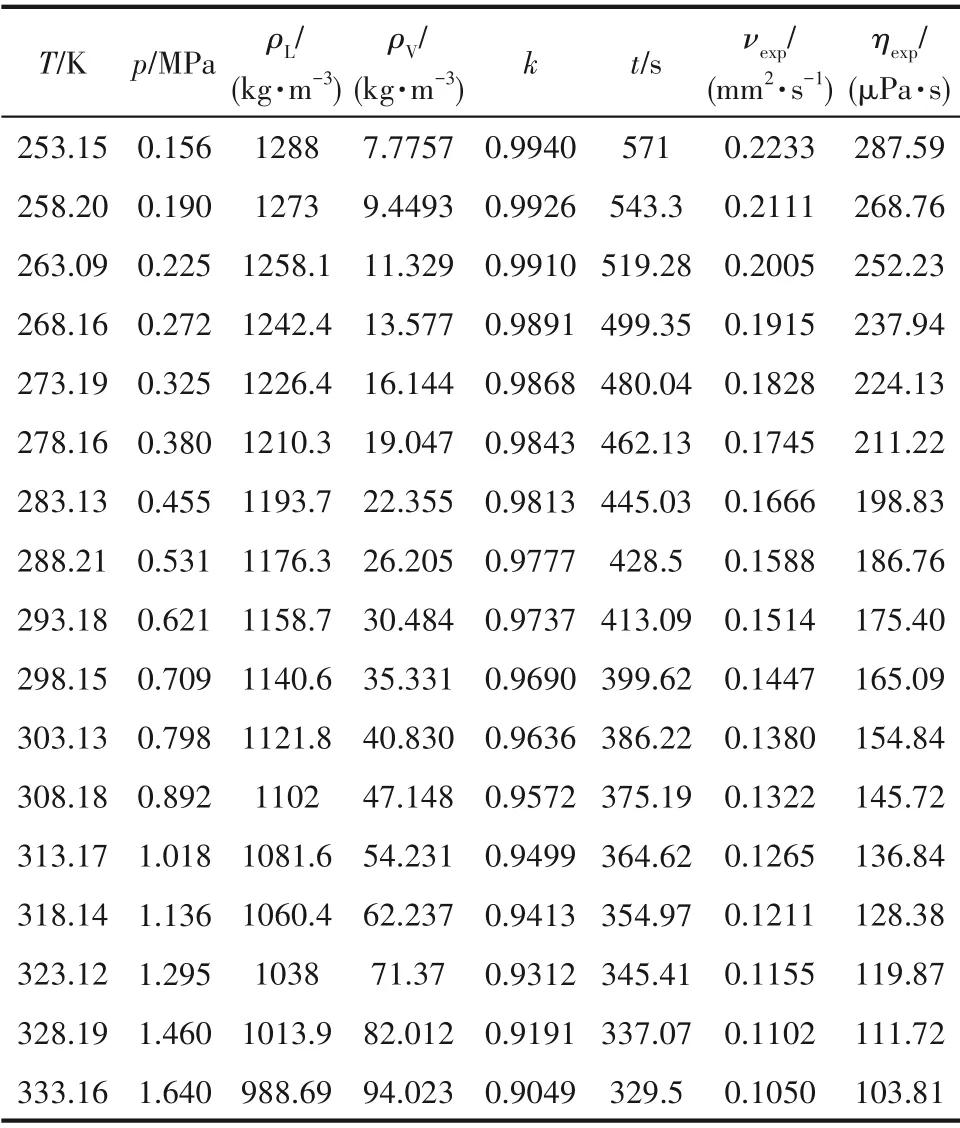
表3 R513A的飽和液相黏度測試結果Table 3 Saturated liquid viscosity experimental results of R513A

流體的流動、傳熱傳質過程與其黏度值緊密相關，黏度小往往意味著流體的流動阻力小，傳熱傳質效果好。因此R513A 是一種非常具有發展前景的制冷劑，在替代R134a的過程中，其黏度特性不會對系統的換熱效果和壓降特性產生額外的影響。

2.2 R513A液相黏度模型預測

2.2.1 R-K 多項式方程 為了方便實際應用，本文基于R513A 飽和液相黏度數據建立了R513A 液相黏度模型。采用多項式方程式（5）和式（6）與R134a和R1234yf 的液相黏度數據進行關聯，其中制冷劑的液相密度值參考REFPROP 9.1[29]，R1234yf 的飽和液相黏度數據參考文獻[30]，擬合結果如表4 所示。利用R-K 多項式方程式（7）與表3 中R513A 的飽和液相黏度實驗數據進行關聯，最終可得擬合參數c和d的值分別為-25.8737 和0.006447。多項式方程的適用溫度范圍為253.15～333.15 K。研究結果表明，R513A 的實驗黏度值與方程計算值的平均絕對偏差為0.71%，最大絕對偏差為1.65%。本文實驗數據與多項式方程計算值的偏差分布如圖4 所示，大部分點的偏差在1.0%以內。模型計算值與實驗數據的擬合效果較好，證明該模型具有較高的精度。

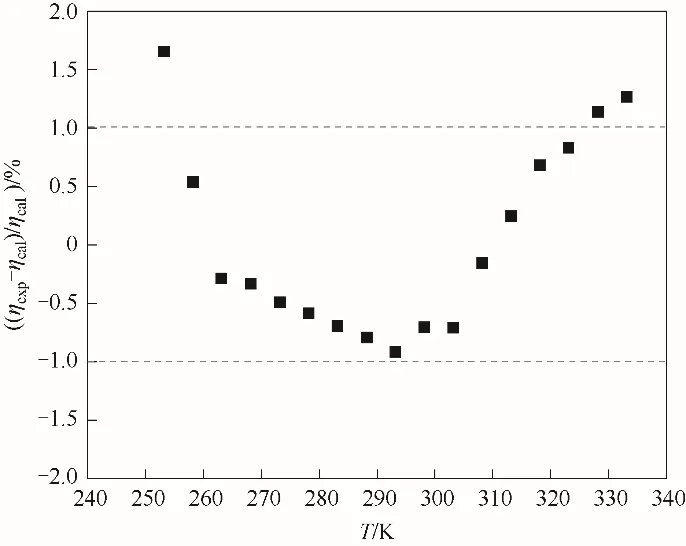
圖4 R513A黏度測試值與R-K方程計算值的偏差分布Fig.4 Deviation between experimental and calculated viscosity of R513A using R-K equation

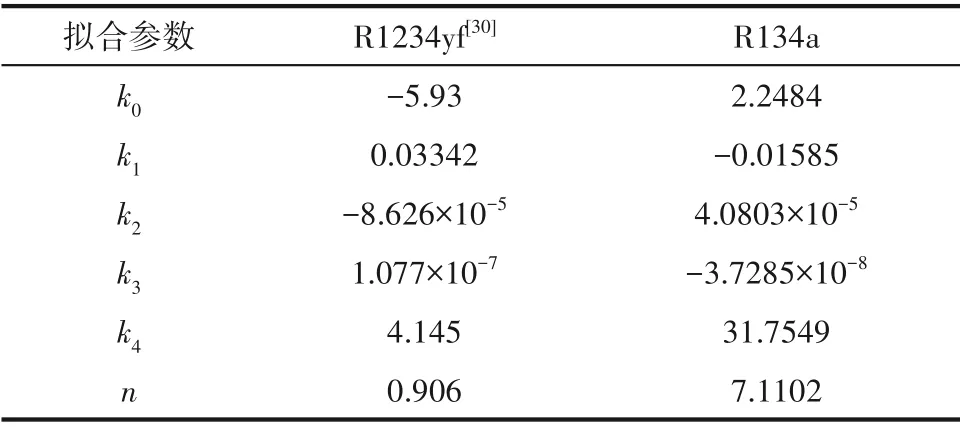
表4 R-K多項式方程擬合參數值Table 4 The fitted value of the R-K polynomial equation

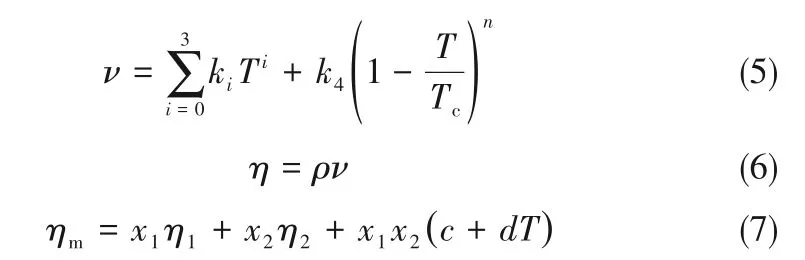
式中，ν為運動黏度，mm2·s-1；ρ為密度，kg·m-3；ηm為混合制冷劑R513A 的液相動力黏度，μPa·s；η1、η2為純制冷劑R1234yf 和R134a 的液相動力黏度，μPa·s；x1、x2為摩爾分數；ki(i=0，1，2，3，4)、n、c、d為擬合參數。

2.2.2 硬球模型 采用硬球模型式（8）～式（11）與R134a和R1234yf的液相黏度數據進行關聯，其中制冷劑的液相密度值參考REFPROP 9.1，R1234yf的飽和液相黏度數據參考文獻[20]，結合混合規則式（12）～式（14）可求得R513A 的液相黏度預測值，擬合結果見表5，模型的適用溫度范圍為253.15～333.15 K。研究結果表明，R513A 的黏度測試值與硬球模型預測值的平均絕對偏差為2.02%，最大絕對偏差為3.39%。針對混合制冷劑，硬球模型無須關聯其實驗黏度值，僅需得知每個組分的比例及液相黏度數據，即可預測得到該混合制冷劑的飽和液相黏度值。對于R513A，硬球模型預測值始終小于黏度測量值，因此所有點的偏差皆為負值，且隨著溫度升高，兩者相對偏差的絕對值增大，如圖5所示。在測試溫度范圍內，模型精度仍處于可接受范圍之內。

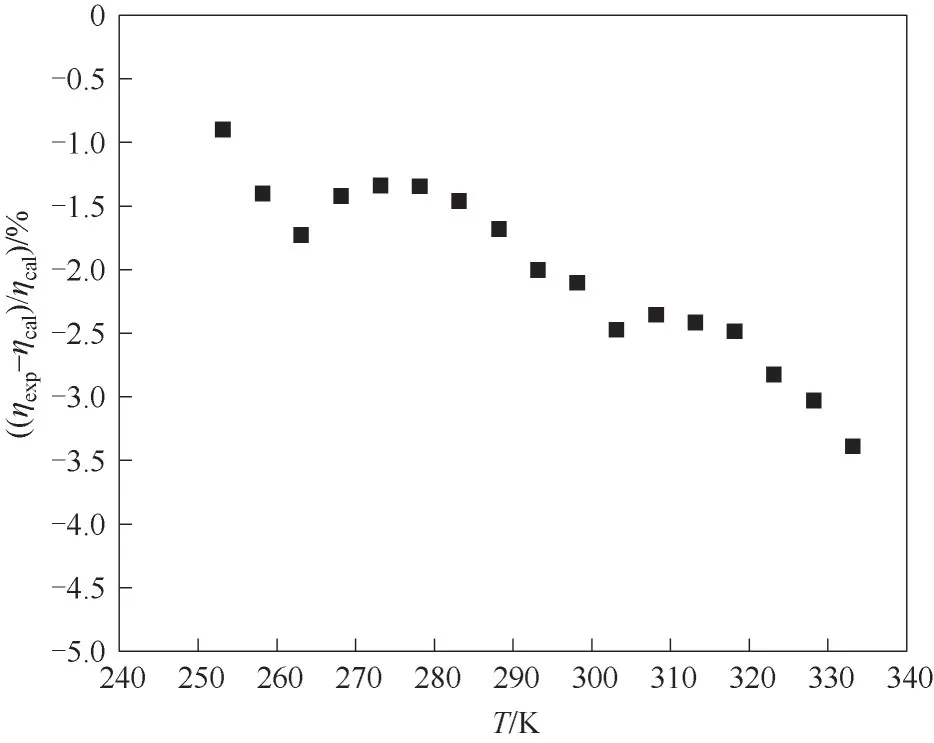
圖5 R513A黏度測試值與硬球模型計算值的偏差分布Fig.5 Deviation between experimental and calculated viscosity of R513A using RHS method

表5 硬球模型擬合參數值Table 5 The fitting parameter values of RHS method

式中，η*為無量綱黏度；M為摩爾質量，kg·mol-1；V為摩爾體積，m3·mol-1；R為普適氣體常數，8.3145 J·mol-1·K-1；η為動力黏度，Pa·s；T為溫度，K。無量綱黏度η*由對比體積Vr所決定，關系式如下：

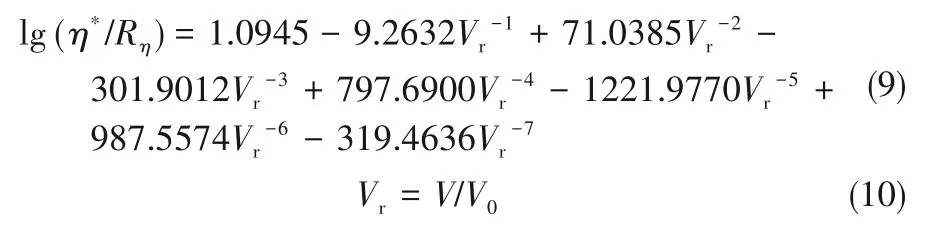
式中，Rη反映了分子平動和轉動之間的耦合程度，與壓力和溫度無關；V0為特征摩爾體積，僅由溫度決定：

硬球模型同樣可以關聯混合制冷劑的黏度特性，二元混合制冷劑的混合規律為：

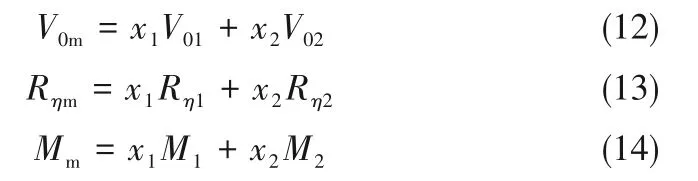
式中，x為組分的摩爾分數；下角標m 代表混合制冷劑R513A，1和2分別代表混合物中的純制冷劑R1234yf和R134a。

R513A 實驗數據、模型計算值及各點相對偏差見表6。R-K 多項式方程需與實驗數據進行關聯，進而計算得到R513A 的飽和液相黏度，其精度要高于硬球模型。而硬球模型僅需得知各組分的比例及液相黏度，即可預測得到R513A 的飽和液相黏度，方便于實際應用。兩種模型都能夠較好地預測混合制冷劑的液相黏度。

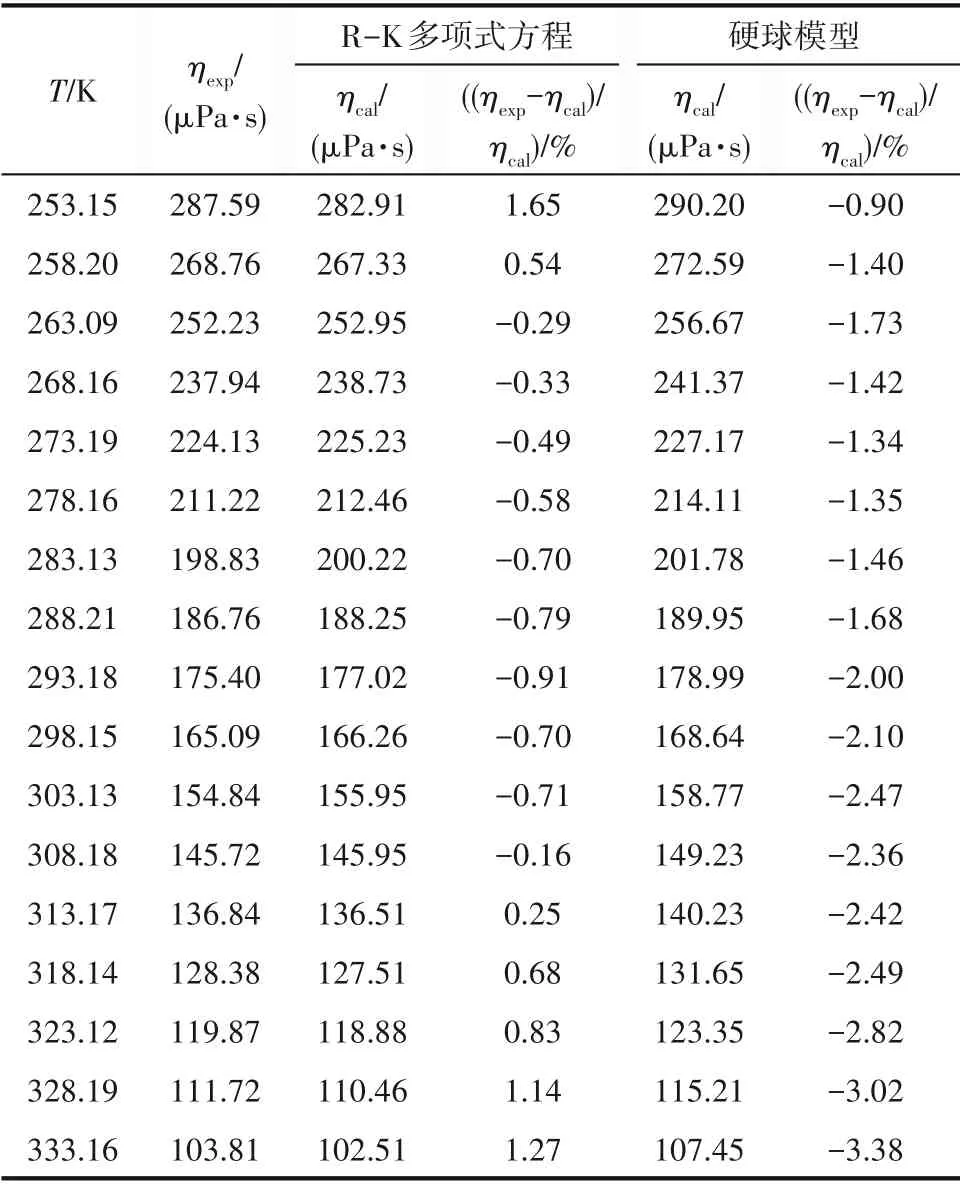
表6 實驗結果與模型計算結果的對比Table 6 Comparison of experimental results and model calculated results

3 結 論

本文基于毛細管法建立了制冷劑液相黏度測試系統，在溫度范圍253.15～333.15 K 內測量R513A的飽和液相黏度，可得出以下結論。

（1）在測試溫度范圍內，R513A 的飽和液相黏度值略低于R134a。

（2）采用R-K 多項式、硬球模型結合混合規則預測了R513A 的飽和液相黏度，實驗黏度值與模型計算值的平均絕對偏差分別為0.71%、2.02%，最大絕對偏差分別為1.65%、3.39%，上述兩種模型的計算值與實驗數據的擬合效果良好。

（3）R-K 多項式方程的精度要高于硬球模型，但硬球模型無須關聯實驗數據，僅需得知各組分的比例及液相黏度數據，即可預測得到混合工質的液相黏度。上述兩種模型都能夠很好地預測R513A的飽和液相黏度，可為其替代應用提供參考依據。

符 號 說 明

M——摩爾質量，kg·mol-1

p——壓力，MPa

R——普適氣體常數，8.3145 J·mol-1·K-1

T——溫度，K

t——流動時間，s

V——摩爾體積，m3·mol-1

x——摩爾分數

η——動力黏度，μPa·s

η*——無量綱黏度

ν——運動黏度，mm2·s-1

ρ——密度，kg·m-3

下角標

L——液相

m——混合工質

V——氣相