近場強地震動特征下的橋梁響應(yīng)探析

羅 娜

(福州市規(guī)劃設(shè)計研究院集團有限公司 福建福州 350000)

0 引言

我國處于地震頻發(fā)地區(qū)，地震具有“頻次多、強度大、分布廣、震源淺”等特點，對橋梁結(jié)構(gòu)的破壞較大。橋梁工程作為交通運輸?shù)闹匾M成部分，是為救災(zāi)活動的生命線工程，若遭到地震的破壞，將導(dǎo)致救災(zāi)困難加大[1]。因此，研究橋梁在地震震動過程中的相應(yīng)規(guī)律，提高橋梁的抗震能力，為采取有效抗震措施提供科學(xué)依據(jù)。

在大地震近場，地震動受震源控制顯著，在近斷裂效應(yīng)的影響下更為復(fù)雜。目前大震近場強震記錄數(shù)量較少，限制了近場地震動的工程破壞效應(yīng)研究進展。2018年2月4日21時56分，中國臺灣花蓮縣附近發(fā)生6.4級地震，震源深度約10 km。此次地震造成17人死亡，295人受傷，至少175幢建筑物受損，4幢坍塌。2月6日23時50分，臺灣花蓮縣附近海域發(fā)生6.5級地震余震，震中位于北緯24.13°、東經(jīng)121.71°，震源深度11.0 km。兩次地震都屬強震，且發(fā)震斷層穿過花蓮城區(qū)，破壞力大，發(fā)震斷層的近場觀測臺站成功收集到了主震和強余震的地震動記錄，部分地震動記錄表現(xiàn)出特殊的近斷裂特性，對研究地震動的近場效應(yīng)及工程破壞作用力非常寶貴。本文利用花蓮地震的大量近場記錄，開展近場強地震動特征研究，分析其對自振周期不同的橋梁結(jié)構(gòu)的破壞作用，為橋梁的抗震設(shè)防設(shè)計和采取抗震措施提供科學(xué)依據(jù)。

1 花蓮地震數(shù)據(jù)下載和處理

1.1 數(shù)據(jù)下載

本文采用從臺灣省地球物理氣象局地球物理數(shù)據(jù)下載中心下載的花蓮地震數(shù)據(jù)[2]，地震時間為2018年2月4日21時56分，并選擇以下19條進場強地震動記錄數(shù)據(jù)，臺站名稱(Station)和震中距(Distance)如表1所示。

表1 花蓮地震數(shù)據(jù)記錄

1.2 數(shù)據(jù)處理

對各原始數(shù)據(jù)進行基線調(diào)整、濾波和積分處理。

首先，基線調(diào)整。消除讀數(shù)器的系統(tǒng)誤差和地震中記錄紙畸變導(dǎo)致的記錄基線誤差。

其次，濾波去除高低頻噪音。采用帶通Butterworth濾波器，高頻和低頻截止頻率分別為0.2Hz和10Hz。濾波前和濾波后的地震動時程對比圖(圖1)，通過圖1可以看出，濾波可較好地去除高低頻噪音。

圖1 典型記錄的濾波對比圖

最后通過積分，得到19個臺站地震動的速度和位移時程圖。以HWA036臺站的水平分量地震動時程圖為例，如圖2所示。

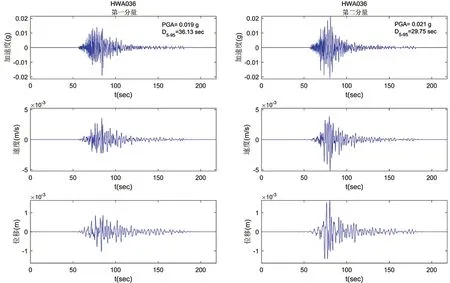
圖2 HWA036臺站的水平分量地震動時程圖

1.3 幅值特征

幅值參數(shù)表征地震動的強度，即表征其對結(jié)構(gòu)物破壞力的大小，對19個臺站兩個水平分量的峰值地面加速度(Peak Ground Acceleration，以下簡稱PGA)、峰值地面速度(Peak Ground Velocity，以下簡稱PGV)、峰值地面位移(Peak Ground Displacement，以下簡稱PGD)按照臺站的震中距升序排列，結(jié)果如表2所示。

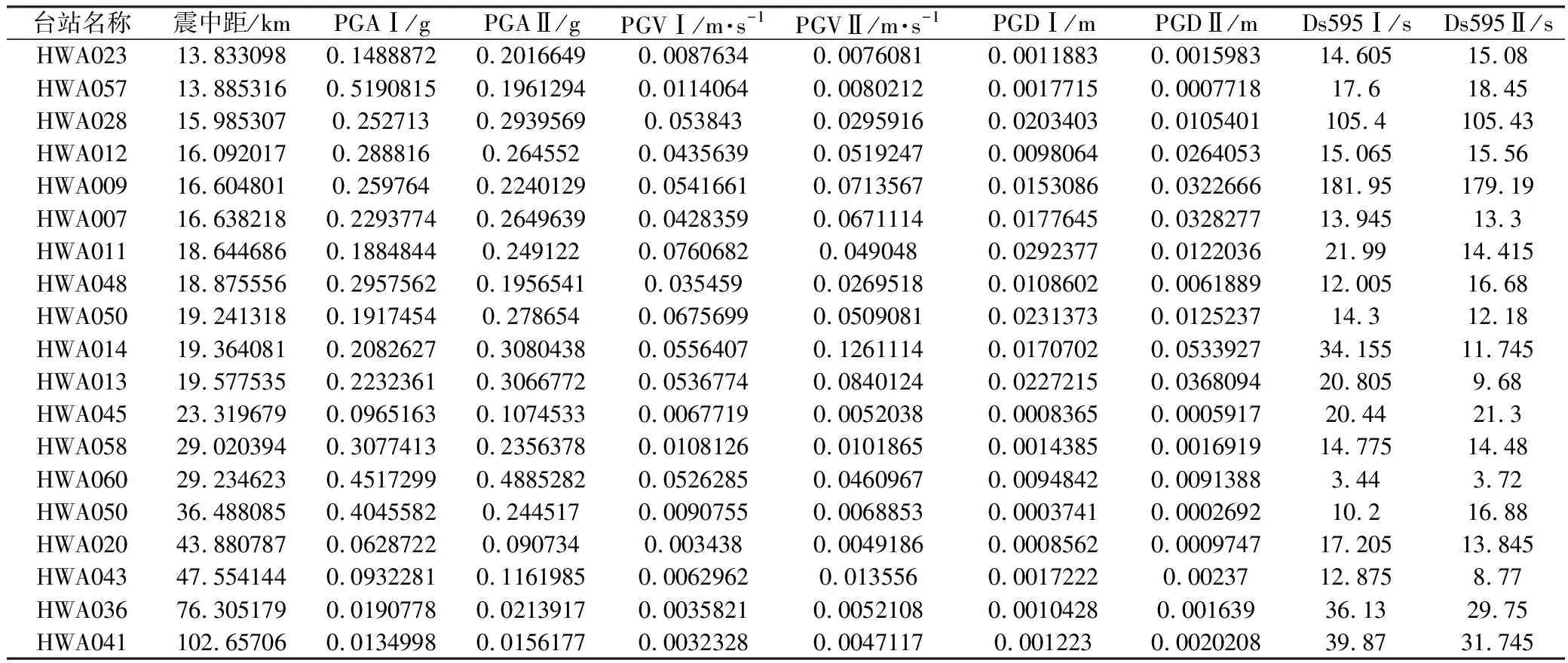
表2 花蓮地震數(shù)據(jù)記錄

根據(jù)表2中的幅值數(shù)值，繪制幅值隨震中距分布的散點圖，如圖3～圖5所示。圖中可見，PGA、PGV和PGD都表現(xiàn)出隨震中距增加而降低的特點。在20 km～30 km處地震動幅值較大，是由于該臺站距離發(fā)震斷層的最小距離，比距離地震破裂起始點的距離更小。

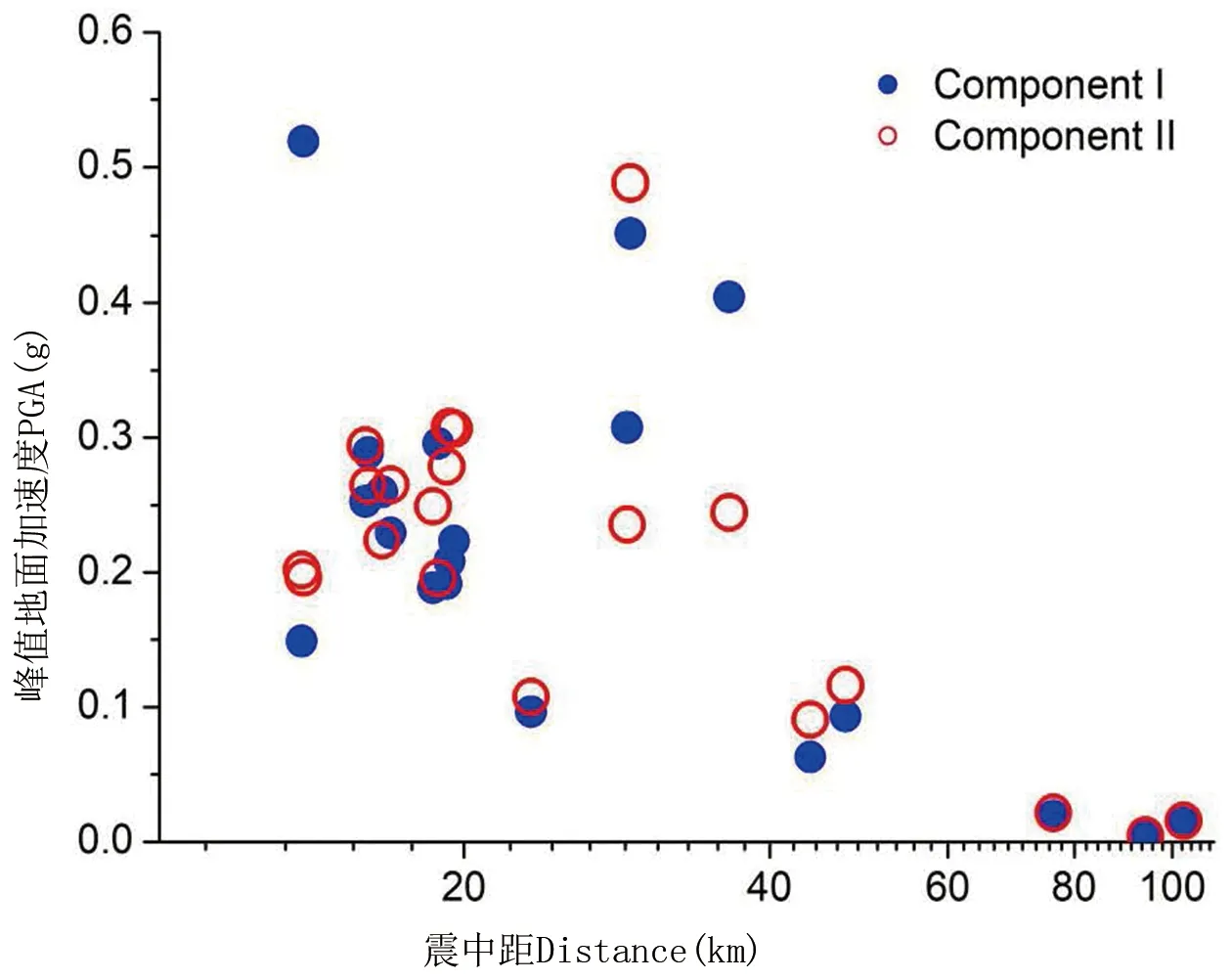
圖3 PGA隨震中距分布圖

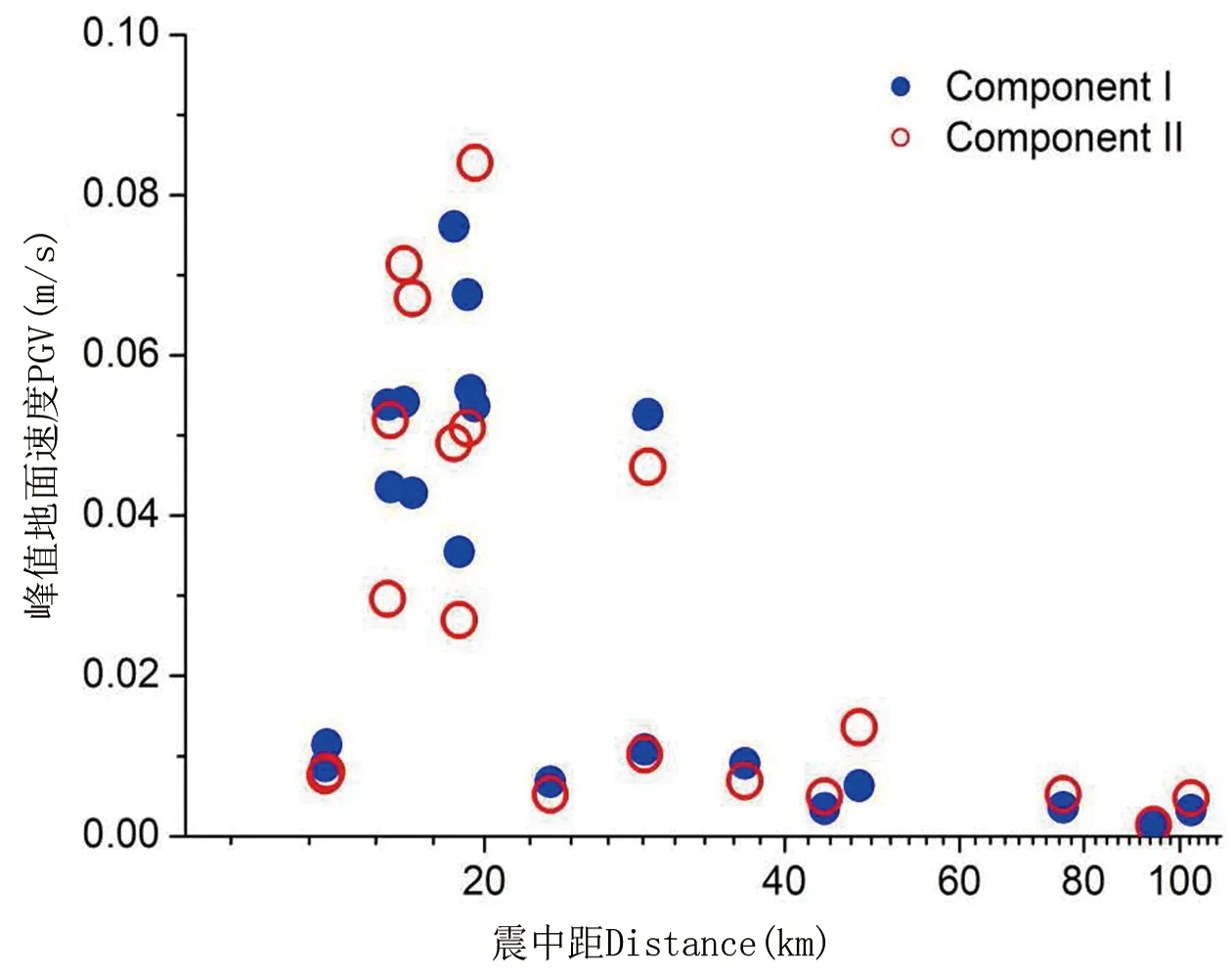
圖4 PGV隨震中距分布圖

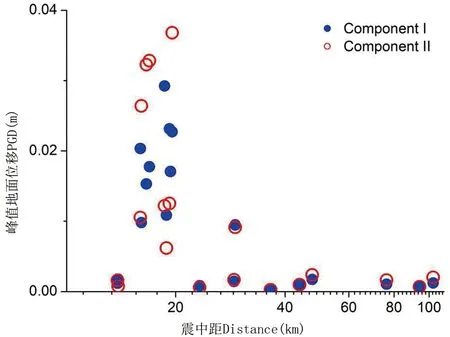
圖5 PGD隨震中距分布圖

1.4 持時特征

持時屬工程結(jié)構(gòu)抗震設(shè)計與研究中不可或缺的地震動參數(shù)之一，目前尚無統(tǒng)一的定義，其種類不下 40余種(Bommer and Martinez，2000)[3]。本文采用較常用的顯著持時作為花蓮地震持時的衡量指標(biāo)。顯著持時基于地震動能量累積過程定義，通過能量達(dá)到兩個規(guī)定閾值之間的時間段確定。工程中常取能量由5%累積至95%之間的時間段，即為5%～95%顯著持時，也是目前應(yīng)用最為廣泛的顯著持時類型；為強調(diào)體波能量，有時也取能量累積由5%～75%之間的時間段，為5%～75%顯著持時，本文討論的顯著持時(Ds)均為5%～95%顯著持時(Ds595)。

本文計算了19個臺站的顯著持時，如表2所示，發(fā)現(xiàn)持時集中在15 s～25 s。同時繪制了顯著持時隨震中距衰減的散點圖，如圖6所示。從圖中可以看出，顯著持時并未表現(xiàn)出明顯的隨震級下降或上升的特征，這也與顯著持時的定義相符。顯著持時的計算，更多決定于時程自身Arias曲線的坡度，而受震中距的影響較小。

圖6 顯著持時隨震中距分布圖

1.5 頻譜特征

頻譜表征組成地震動時程的各頻率成分的振幅、能量等信息，通過對地震動的頻譜分析，可以發(fā)現(xiàn)，地震動中能量較為顯著的頻率組成，從而判斷其對不同結(jié)構(gòu)物的影響。本文利用Matlab語言編制計算幅值、持時和傅立葉譜、反應(yīng)譜的程序，并通過程序計算19個臺站兩分量地震記錄的加速度、速度、位移反應(yīng)譜和傅立葉譜，部分臺站的傅立葉譜和反應(yīng)譜圖如圖7所示。

圖7 HWA036和HWA014臺站的加速度、速度、位移傅立葉譜和反應(yīng)譜圖

由圖中可知，花蓮地震記錄的短周期成分非常顯著，大部分臺站卓越周期都位于1 s以上周期段，這類地震動記錄，對自振周期較長的構(gòu)筑物可能產(chǎn)生較大影響。

2 橋梁結(jié)構(gòu)響應(yīng)分析

2.1 計算模型

本文采用一橋長19.96 m，橋面凈空為7 m+2×0.75 m人行道的鋼筋混凝土簡支T型橋為具體算例，混凝土采用C30，主筋用HRB335鋼筋，其他用R235鋼筋，全斷面五片主梁，設(shè)五根橫梁。在有限元分析軟件Midas Civil中建模，靜力工況考慮橋面鋪裝和人行道鋪裝和自重。

同時建立另一個橋梁結(jié)構(gòu)模型，邊界條件處即與基礎(chǔ)的連接、橋面和墩臺的連接進行不同設(shè)置，從而兩個橋梁模型的自振周期不同。A橋(自振周期1 s)和B橋(自振周期0.6 s)。A、B兩橋有限元模型如圖8～圖9所示。

圖8 A橋計算模型(長周期)

圖9 B橋計算模型(非長周期)

A模型共196個單元，187個節(jié)點。B模型共196個單元，189個節(jié)點。采用時程分析法進行橋梁結(jié)構(gòu)地震響應(yīng)分析。在開展分析前，對橋梁結(jié)構(gòu)先行開展振型分析，可以得到橋梁的各項動力特性值，包含振型形狀或振型形象、固有周期、固有頻率、振型參與系數(shù)、振型參與質(zhì)量等。

本文首先將橋面鋪裝和人行道鋪裝荷載轉(zhuǎn)化為質(zhì)量；然后定義特征值分析控制信息。常用的振型分析方法有子空間迭代法、Lanczos方法和多重Ritz向量法，本文采用Lanczos方法，能比子空間迭代法計算速度快4～10倍。

《公路橋梁抗震設(shè)計細(xì)則》(JTG/TB02-01-2008)規(guī)定[4]，需保證參與系數(shù)達(dá)到 90% 以上，這是盡可能包含對分析結(jié)果有影響的大部分主要振型。本文A、B兩橋在順橋向和橫橋向的參與系數(shù)總和均已符合規(guī)范規(guī)定要求，其中最高為96.95%，最低為93.10%。B橋在輸入一條地震波的反應(yīng)結(jié)果，如表3所示。

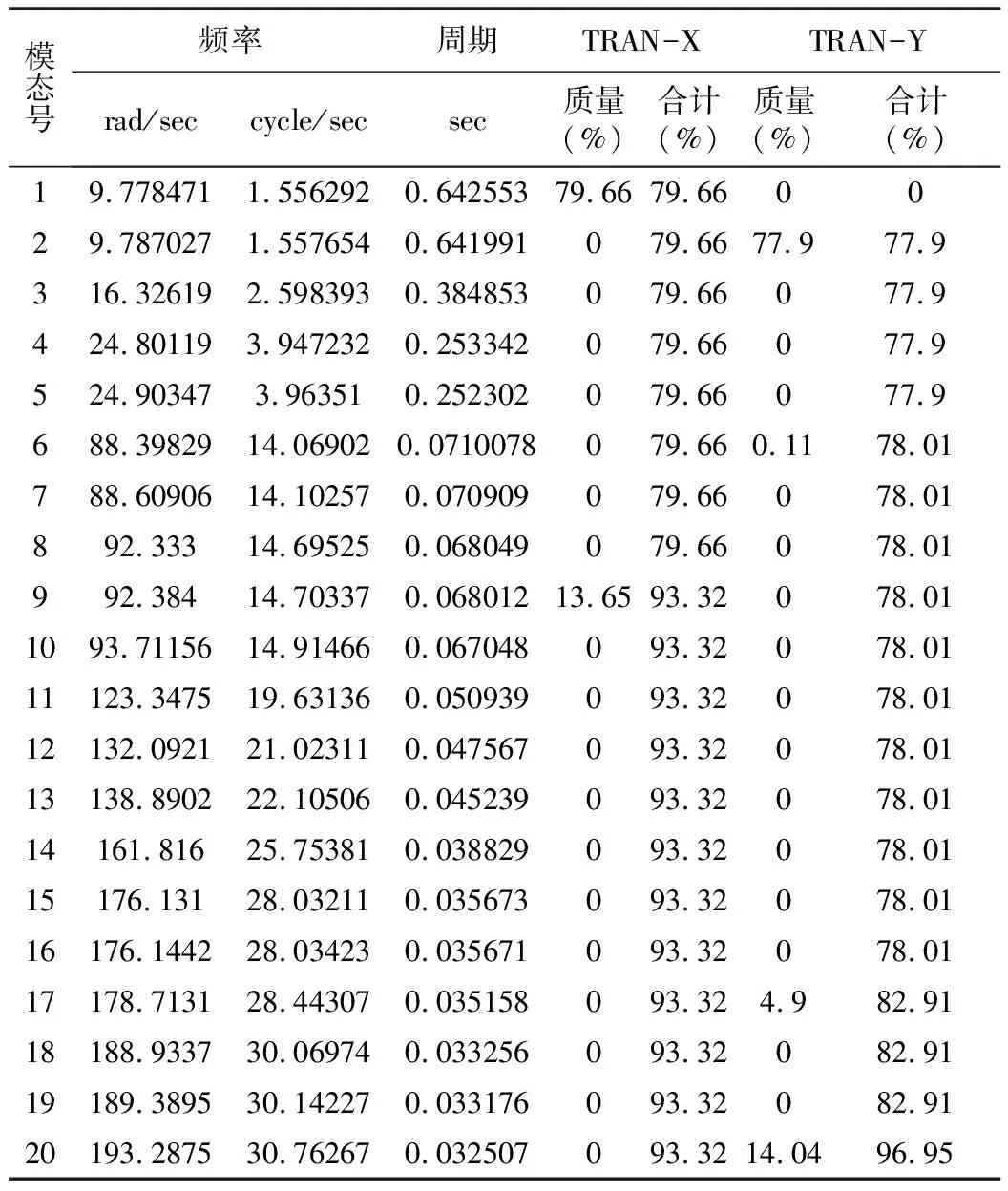
表3 B橋特征值模態(tài)

2.2 響應(yīng)結(jié)果

取本次臺灣花蓮地震三組地震動時程，同樣動力時程反應(yīng)的地震激勵采用順橋向和橫橋向2種方式，結(jié)構(gòu)動力反應(yīng)的荷載組合為2向地震力加恒載作用，選取阻尼比為0.05，分析步長為0.005 s，A、B兩橋各控制截面(支座和跨中截面)的部分內(nèi)力、位移等結(jié)果如圖10～圖17所示。

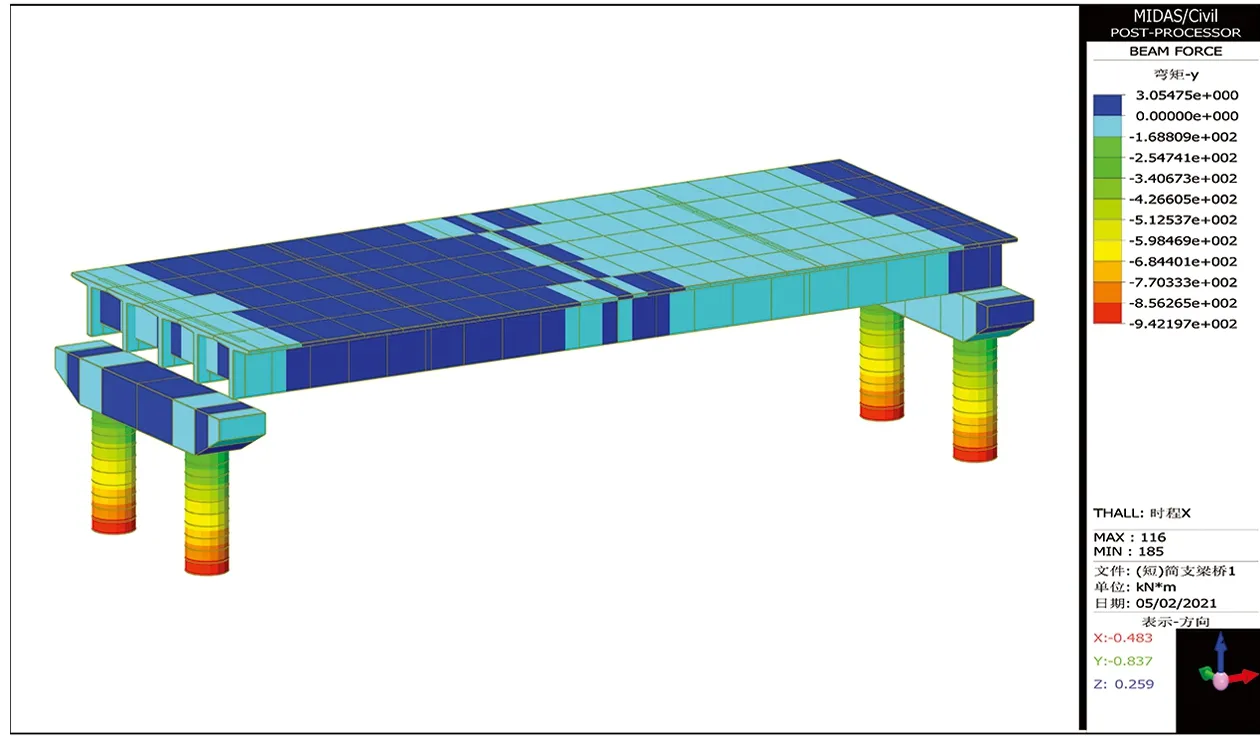
圖10 A橋在順橋向激勵下的MY

圖11 B橋在順橋向激勵下的MY

圖12 A橋在橫橋向激勵下的MY

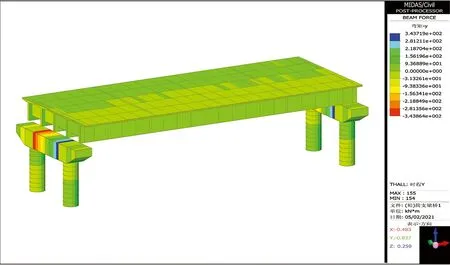
圖13 B橋在橫橋向激勵下的MY

圖14 A橋跨中在順橋向激勵下的水平方向時程數(shù)據(jù)

圖15 B橋跨中在順橋向激勵下的水平方向時程數(shù)據(jù)

圖16 A橋在順橋向激勵下的X向位移

圖17 B橋在順橋向激勵下的X向位移

2.3 響應(yīng)分析的結(jié)論

通過A、B橋梁相應(yīng)結(jié)果數(shù)據(jù)對比，發(fā)現(xiàn)在選取的花蓮地震近場強地震動輸入的情況下，自振周期長的A橋橋梁受地震激勵后，內(nèi)力反應(yīng)如彎矩、位移等均遠(yuǎn)遠(yuǎn)大于B橋，證明花蓮地震顯著的周期成分，會引起自振周期較長的構(gòu)筑物的較大反應(yīng)。

3 結(jié)語

本文選取2018年花蓮地震的部分近場強地震動記錄，通過數(shù)據(jù)處理后計算每條地震動時程的幅值、持時、頻譜特征等三要素，并探討地震動三要素的空間變化特征，重點探討由方向性效應(yīng)引起的地震動周期特征引起的橋梁結(jié)構(gòu)響應(yīng)。以典型鋼混簡支T型橋梁結(jié)構(gòu)為例，建立結(jié)構(gòu)分析模型，選取3個花蓮地震近場強地震動加速度時程記錄分別輸入不同振動周期的橋梁模型，分析花蓮地震記錄引起的橋梁結(jié)構(gòu)響應(yīng)特征，得出了以下幾點結(jié)論：

(1)大部分花蓮地震記錄都表現(xiàn)出顯著的短周期特征，PGA、PGV和PGD都表現(xiàn)出隨震中距增加而降低的特點，大部分記錄的卓越周期都位于1 s左右周期段。

(2)將花蓮地震記錄輸入自振周期分別為0.6 s和1 s的鋼筋混凝土簡支梁橋，對結(jié)構(gòu)進行響應(yīng)分析，發(fā)現(xiàn)自振周期較長的橋梁模型給出的響應(yīng)更大，甚至嚴(yán)重破壞，從而證明短周期成分顯著的花蓮近場地震記錄，對自振周期為1 s的橋梁造成更多的不利影響。

(3)采用動力時程分析法來分析橋梁地震響應(yīng)，考慮了地震動的三要素和結(jié)構(gòu)的非線性問題。但計算較為復(fù)雜，并且需要對計算結(jié)果進行統(tǒng)計分析，有一定的應(yīng)用局限性。