基于LSTM循環(huán)神經網(wǎng)絡的橫波預測方法

周恒 ，武中原 ，張欣 ，張春雷 ，馬喬雨

（1.中國地質大學（北京）數(shù)理學院，北京 100083；2.北京師范大學統(tǒng)計學院，北京 100875；3.北京中地潤德石油科技有限公司，北京 100083）

0 引言

碳酸鹽巖儲層已探明石油、天然氣儲量分別占全國石油、天然氣儲量的8%和28%，是重要的油氣勘探目標[1-4]。但該類儲層具有巖性多樣、非均質性強、孔隙結構復雜的特點，給測井解釋帶來很大難度[5-7]。橫波速度是進行碳酸鹽巖儲層評價、流體識別和疊前正反演必需的基礎資料，將測井參數(shù)與縱橫波速度資料相結合，可以有效提升儲層物理參數(shù)預測效果和地震振幅解釋效果[8-11]。不同于常規(guī)測井，橫波速度通常需要通過偶極子聲波得到。由于測試價格昂貴、測試結果較差、橫波測井解釋難度較高等諸多問題，實際生產中往往缺失橫波速度資料，因此，開展碳酸鹽巖儲層的橫波預測具有重要的意義[12-13]。

目前常用的橫波預測方法主要有3種——經驗公式法[14-17]、理論模型法[18-20]、機器學習法[21-22]。 經驗公式法往往只適用于某一地區(qū)，缺乏泛用性，理論模型法參數(shù)眾多且預測效果較差，因此近年來機器學習法得到迅速發(fā)展，在地質領域逐漸成為研究熱點。傳統(tǒng)的機器學習法，如決策樹、支持向量機、多元線性回歸等，是根據(jù)特定的學習準則構建測井參數(shù)與橫波之間的映射關系，但忽略了連續(xù)變量的序列特征。循環(huán)神經網(wǎng)絡（RNN）能夠在一定程度上解決序列數(shù)據(jù)的前后關聯(lián)問題，但由于梯度爆炸和梯度消失問題而效果不佳[23]。長短時記憶神經網(wǎng)絡（LSTM）[24]是一種改進的 RNN，在有效提取序列特征的同時，引入門控單元，實現(xiàn)長短時信息的有效記憶，能夠控制長短時信息的遺忘與更新，表達不同測井參數(shù)的尺度承載能力和橫波的沉積序列特征，挖掘測井參數(shù)與橫波之間的深層聯(lián)系。

以鄂爾多斯盆地蘇里格氣田蘇東地區(qū)碳酸鹽巖儲層為例，開展了基于LSTM方法的橫波預測方法研究。首先，通過測井資料與測井參數(shù)敏感性分析，選擇與橫波時差相關的16種測井參數(shù)；然后，構建基于LSTM的橫波時差預測模型，并與多種機器學習方法進行對比，分析LSTM在橫波預測中的具體表現(xiàn)。

1 方法原理

1.1 RNN

RNN是一種針對序列數(shù)據(jù)特征提取的神經網(wǎng)絡。傳統(tǒng)的BP神經網(wǎng)絡沒有考慮數(shù)據(jù)的時序性，因而在處理序列特征時效果較差。RNN引入自循環(huán)單元后，不但能夠充分考慮當前信息，還能有效學習隱變量傳遞的歷史信息，從而具有一定的“記憶”功能。RNN在每次模型預測時不僅考慮了當前輸入信息，也考慮了之前所有的歷史信息。RNN的鏈式結構與序列數(shù)據(jù)建模契合，使得RNN在序列數(shù)據(jù)分析中具有較大優(yōu)勢，成為解決序列數(shù)據(jù)最自然的結構。

為避免復雜的參數(shù)學習，RNN在所有時間維度上實現(xiàn)參數(shù)共享，在簡化網(wǎng)絡模型的同時，能夠學習任意長度的序列數(shù)據(jù)。相較于BP神經網(wǎng)絡，RNN每個神經元具有 2 個輸入信息（xt，ht-1）和 2 個輸出信息（ot，ht）。xt為t時刻的輸入信息，ht-1為t-1時刻輸出（即t時刻輸入）的隱狀態(tài)信息，ht為t時刻輸出的隱狀態(tài)信息，ot為t時刻的輸出信息。RNN循環(huán)單元的計算公式為

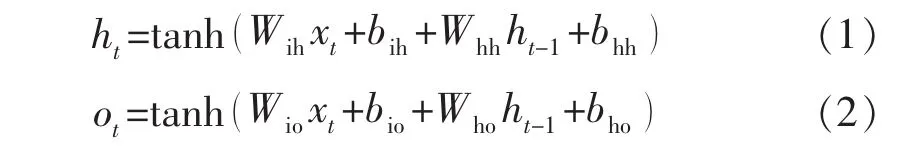
式中：Wih為輸入門與隱狀態(tài)間的權重；bih為輸入門與隱狀態(tài)間的偏置；Whh為隱狀態(tài)間的權重；bhh為隱狀態(tài)間的偏置；Wio為輸入門與輸出門間的權重；bio為輸入門與輸出門間的偏置。

Wih和Whh對序列長度較為敏感。當序列較長時，循環(huán)單元很難依靠隱狀態(tài)記憶長時序的信息，在反向傳播時就會導致RNN梯度爆炸或者梯度消失，使得RNN無法有效學習序列特征。

1.2 LSTM

LSTM 由 Hochreiter等[24]于 1997 年提出，與 RNN對歷史信息的簡單疊加不同，LSTM通過3個門層對當前信息和歷史信息進行選擇；同時，LSTM引入細胞狀態(tài)傳遞長序列信息，能夠綜合局部信息和序列信息，實現(xiàn)長短時記憶；LSTM具有類似RNN的循環(huán)網(wǎng)絡結構，且增加了控制器操作信息的丟棄和增加，從而實現(xiàn)遺忘和記憶功能。門控制器是一種選擇信息的結構，包含一個sigmoid函數(shù)和一個點乘操作。其中，sigmoid函數(shù)將輸入值約束在[0，1]，從而控制信息的學習承擔，0代表完全舍棄，1代表完全學習。

LSTM的基本循環(huán)單元（見圖1）主要包括3個門層（輸入門、輸出門、遺忘門）和1個狀態(tài)更新層。輸入門控制信息的輸入，遺忘門控制歷史信息的保留，輸出門控制信息的輸出，狀態(tài)更新層控制狀態(tài)信息的更新。各門層計算公式見表1。表中：ft為t時刻遺忘門的輸出；σ為sigmoid函數(shù)；it為t時刻輸入門的輸出；為t時刻 tanh層的輸出；Ct，Ct-1分別為 t，t-1時刻的細胞狀態(tài)；W 為權重；b 為偏置；下標 f，i，c，o分別表示遺忘門、輸入門、狀態(tài)更新層、輸出門。

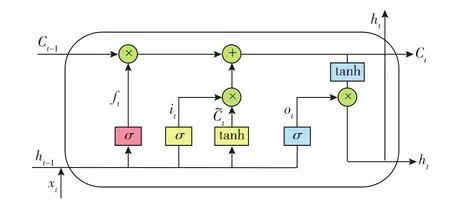
圖1 LSTM循環(huán)單元結構

表1 LSTM各門層計算公式

LSTM在進行網(wǎng)絡學習時，首先通過遺忘門和輸入門對當前的輸入信息和前一時刻的隱狀態(tài)進行學習，去除細胞狀態(tài)中需要遺忘的歷史序列信息，選出有用的當前序列信息加入到細胞狀態(tài)，然后在輸出門根據(jù)更新后的細胞狀態(tài)提供長期序列信息，結合當前輸入信息和前一時刻隱狀態(tài)實現(xiàn)隱狀態(tài)更新。在每次迭代中，LSTM能夠根據(jù)當前輸入信息更新細胞狀態(tài)和隱狀態(tài)，保持序列信息的有效學習。

2 實例分析

2．1 數(shù)據(jù)背景

研究區(qū)位于內蒙古自治區(qū)烏審旗境內，南鄰陜西省靖邊縣，東鄰陜西省橫山縣。區(qū)域構造位于鄂爾多斯盆地伊陜斜坡北部，下古生界的馬家溝組五段碳酸鹽巖為其重要的含氣儲層，巖性主要包括白云巖、泥質白云巖、石灰質白云巖、泥質石灰?guī)r、白云質石灰?guī)r和石灰?guī)r，孔隙類型主要有粒間孔、溶孔、膏模孔和少量微裂縫，孔隙流體為天然氣和水。

選取與橫波時差（SAC）相關的16個測井參數(shù)：縱波時差（AC）、補償中子（CNL）、密度（DEN）、自然伽馬（GR）、自然電位（SP）、光電吸收截面指數(shù)（PE）、深側向電阻率（RLLD）、淺側向電阻率（RLLS）、陣列感應電阻率（RT10，RT20，RT30，RT60，RT90）、鉀的質量分數(shù)（w（K））、釷的質量濃度（ρ（TH））、鈾的質量濃度（ρ（U））。參數(shù)特征如圖2所示。

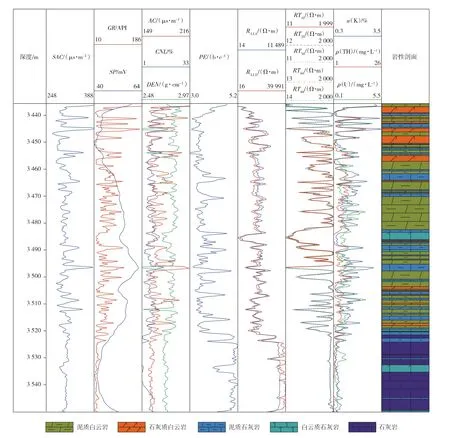
圖2 研究區(qū)測井參數(shù)特征

傳統(tǒng)巖石物理模型表明，橫波預測過程受巖石礦物、孔隙結構、孔隙流體等因素的影響，因此，不同測井參數(shù)對橫波速度都有一定指示作用。從所選測井參數(shù)與橫波時差之間的相關性可以看出，不同測井參數(shù)之間具有相關性，且都與橫波時差存在一定的聯(lián)系。不同巖石的孔隙流體、孔隙結構、礦物特征均不同，導致測井參數(shù)差異較大，最終表現(xiàn)為橫波時差的不同，因此，綜合這些測井參數(shù)，能夠有效表達儲層的橫波特征。

2．2 模型構建

傳統(tǒng)的橫波預測方法往往針對某一特定儲層，泛化性較差；而深度學習法是一種數(shù)據(jù)驅動方法，能夠自適應地提取相關特征，構建測井參數(shù)與橫波時差之間的深層次映射，具有較強的泛化性。圖3為本研究提出的基于LSTM方法的橫波預測流程。構建橫波預測模型時，首先需要數(shù)據(jù)標準化，這樣能夠有效避免量綱對模型學習的影響，并顯著提升模型訓練速度（常用的標準化方法是均值方差標準化，轉化后的數(shù)據(jù)服從標準正態(tài)分布）；然后需要對測井參數(shù)進行轉換，得到包含局部時序特征的測井參數(shù)；最后構建LSTM模型進行網(wǎng)絡學習，和多種機器學習方法對比，評估LSTM模型的表現(xiàn)。由于橫波預測是回歸問題，LSTM使用均方根誤差（RMSE）和決定系數(shù)（R2）對模型預測結果進行評估，同時使用Adam優(yōu)化器加速網(wǎng)絡學習，為防止網(wǎng)絡過擬合，還引入了dropout提升模型的泛化能力。

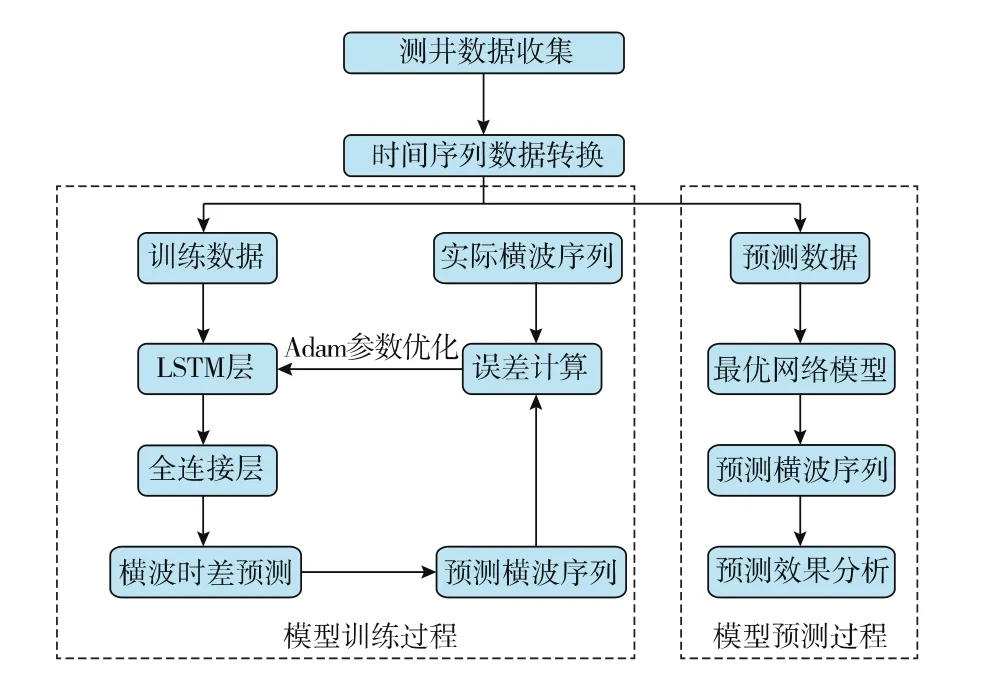
圖3 基于LSTM的橫波預測流程

2.3 結果分析

數(shù)據(jù)總樣本數(shù)為2 904個，橫波預測模型建立過程中隨機選取50%的樣本集作為訓練集，其余50%作為驗證集，時間步長為8，dropout設置為0.25，網(wǎng)絡使用2個LSTM層和3個全連接層，激活函數(shù)為RELU，學習率為0.001。為驗證LSTM的穩(wěn)健性和泛化能力，選擇貝葉斯回歸（Bayes）、BP 神經網(wǎng)絡（BP）、K 近鄰回歸（KNN）、決策樹（DT）、線性回歸（LR）、支持向量機（SVM）等機器學習方法，以及傳統(tǒng)巖石物理模型方法中的Xu-Payne模型一起進行對比。根據(jù)研究區(qū)地質背景分析和碳酸鹽巖儲層特征，將Xu-Payne模型簡化為白云石、方解石、泥質3種礦物，少量的粒間孔、溶孔、微裂縫3種孔隙類型，以及天然氣和水2種孔隙流體。傳統(tǒng)的Xu-Payne模型預測橫波時差，首先是通過測井解釋得到方解石、白云石和泥質的體積分數(shù)、孔隙度、含氣飽和度，同時根據(jù)已知的縱波速度和密度，采用模型進行橫波預測，然后根據(jù)文獻[25]確定模型計算過程中所用的礦物及流體組分。

2.3.1 定性分析

從定性角度分析不同方法的橫波預測結果（見圖4）。由圖可知：1）機器學習方法的精度明顯高于Xu-Payne模型，表明機器學習方法能夠更加有效地提取測井參數(shù)本身的特征，從而構建精度更高的預測模型。2）基于LSTM的預測結果精度最高，而其他的機器學習方法則在一些層位出現(xiàn)較大的誤差。比如在橫波波動較大的3 515 m處，多數(shù)機器學習方法的預測結果都出現(xiàn)了較大偏差；在橫波相對平緩的3 485 m處，Bayes和LR的預測結果波動較大，而LSTM的結果則和實際情況相符。

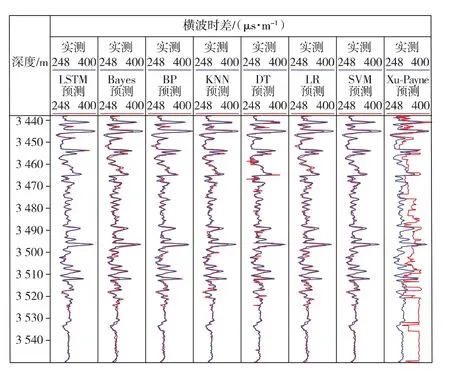
圖4 不同方法的橫波預測結果

2.3.2 定量分析

從定量角度分析不同機器學習方法的橫波預測結果（見表1）。由表可知，LSTM在不同巖性、流體中均取得最佳預測結果。1）從巖性來看，石灰?guī)r、白云質石灰?guī)r、白云巖和石灰質白云巖結構較為復雜，在實際學習過程中，這幾類巖性的橫波預測結果相差較大，這是因為不同方法采取的學習策略不同，學習特征不平衡，從而在面對復雜儲層結構時，預測精度呈現(xiàn)出較大的差異；而LSTM對不同巖性的橫波預測精度均在0.850以上，這也表明LSTM能夠通過特有的時序結構，有效提取測井參數(shù)序列特征，實現(xiàn)測井參數(shù)與橫波時差之間的整體匹配，從而對不同巖性都能實現(xiàn)有效識別，具有更強的泛化性。2）從流體來看，BP和SVM能夠有效提取干層的橫波特征，而在預測氣水同層時不能有效學習，精度較低；Bayes和KNN等方法的學習策略較為簡單，對2種流體的學習精度都偏低；LSTM則可以有效提取干層和氣水同層橫波特征，預測精度較高。

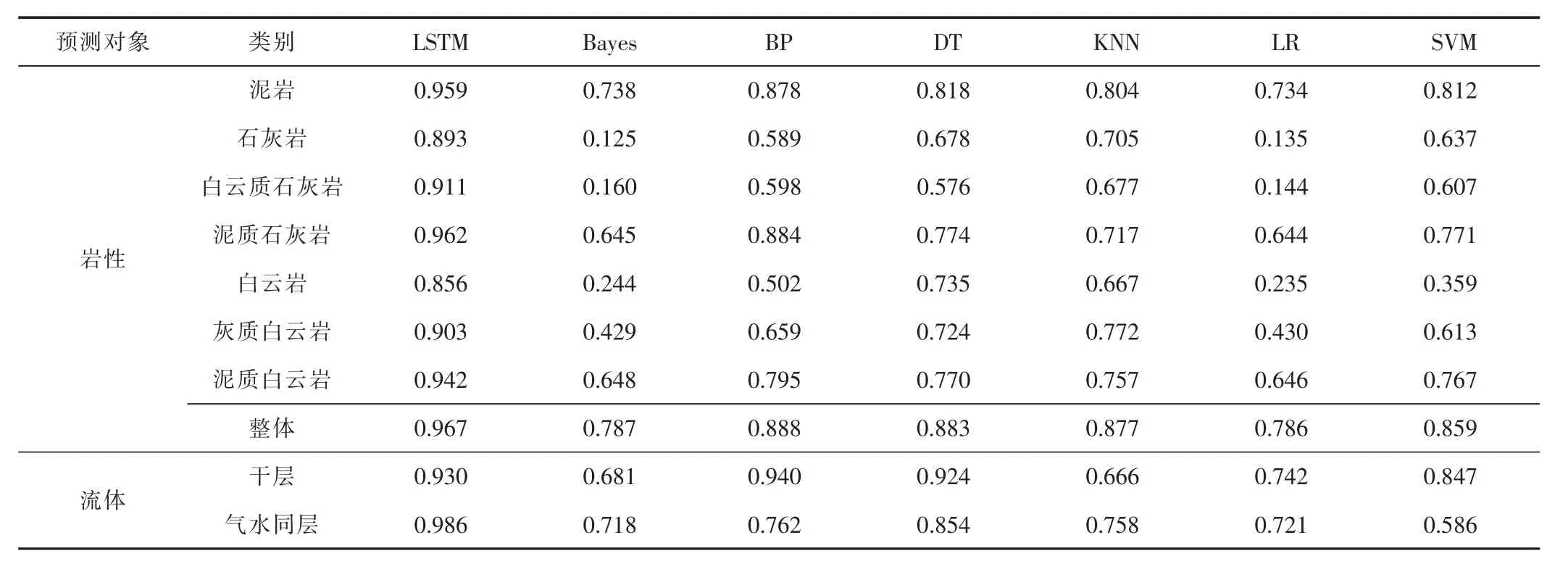
表1 不同機器學習方法預測橫波時差的決定系數(shù)

2.3.3 誤差統(tǒng)計

為進一步分析LSTM的橫波預測效果，對不同機器學習法預測橫波時差的絕對誤差（以下簡稱誤差）進行統(tǒng)計。總的來說，LSTM的誤差不超過20 μs/m，而其他方法的誤差最高達到60 μs/m，這也體現(xiàn)了LSTM方法具有較高的魯棒性。從局部來看：LSTM的誤差分布較為均衡，沒有出現(xiàn)較大偏差；Bayes，LR和SVM在橫波時差極值附近的誤差較大，達到40 μs/m左右，說明這些方法在面對橫波劇烈變化時不能有效捕捉序列特征，從而導致預測效果較差。從整體來看：BP和KNN大部分預測結果都與原始數(shù)據(jù)存在10～20 μs/m的差值；LSTM除了少部分波動點外，絕大部分預測誤差都在10 μs/m以內，說明LSTM能夠根據(jù)數(shù)據(jù)本身的序列特征，深度挖掘測井參數(shù)與橫波的整體匹配模式，構造符合實際地質情況的高精度橫波預測模型。

2.3.4 特征組合

為分析測井參數(shù)對碳酸鹽巖儲層不同巖性、流體中橫波時差預測的影響，按照不同測井參數(shù)在地質分析中的相關性與獲取的難易程度，確定4種特征組合方案：V6（AC，CNL，DEN，GR，PE，SP），V8（V6 基礎上加入 RLLD和 RLLS），V13（V8 基礎上加入 RT10，RT20，RT30，RT60，RT90），V16（V13 基礎上加入w（K），ρ（TH），ρ（U））。預測結果如表2所示。

表2 不同特征組合方案的橫波預測精度

由表2可知：1）和 V6相比，V8加入 RLLD和RLLS后，石灰?guī)r、白云質石灰?guī)r的橫波預測精度有所上升，而白云巖、石灰質白云巖、泥質白云巖的橫波預測精度下降，從而導致整體橫波預測精度較差，這也表明電阻率可以指示部分石灰?guī)r特征。2）V13的精度相比V8有較大的提升，表明加入陣列感應電阻率后，多個電阻率可以有效指示儲層孔隙和流體結構，從而提升識別效果。3）V16的精度最高，表明加入伽馬能譜后，網(wǎng)絡能夠聯(lián)合GR信息，對包含泥質的巖性部分橫波特征作進一步的補充，從而提升了整體的預測精度。綜合4種方案可以看出：使用8種測井參數(shù)的預測效果最差，使用16種測井參數(shù)的預測效果最好，R2達到了0.967，RMSE 減小至 3.360 μs/m。

3 結論

1）LSTM能夠從測井參數(shù)本身出發(fā)，有效表達不同測井參數(shù)的序列特征。不同于點對點的機器學習方法，基于LSTM的橫波預測模型能夠有效捕捉到橫波時差沉積模式和測井參數(shù)承載尺度信息，實現(xiàn)了測井序列和橫波序列的整體匹配。

2）和傳統(tǒng)的機器學習方法和Xu-Payne模型相比，LSTM的橫波時差預測精度更高，絕對誤差在20 μs/m以內，決定系數(shù)達到0.967，且在不同巖性中均取得最優(yōu)預測結果，表明LSTM具有較強的泛化性，能夠挖掘出測井參數(shù)與橫波之間的內在聯(lián)系。

3）在使用6種常規(guī)測井參數(shù)時，LSTM也能取得較好的精度；只有將側向電阻率和陣列感應電阻率相結合，才能對地層中的孔隙與流體結構起到良好的指示作用；伽馬能譜對自然伽馬曲線的補充，能夠進一步提升LSTM的預測精度。

4）LSTM是一種高效的數(shù)據(jù)挖掘模型，通過控制3個門層保證信息的連續(xù)性，實現(xiàn)了測井參數(shù)序列特征的自動提取，在巖石物理參數(shù)的數(shù)據(jù)挖掘上具有廣闊的應用前景。