介觀平行板電容器間帶電微粒的透射問題*

吳仍來

(惠州學院電子信息與電氣工程學院 廣東 惠州 516007)

肖世發

(嶺南師范學院物理科學與技術學院 廣東 湛江 524048)

楊昌彪

(嶺南師范學院附屬中學 廣東 湛江 524048)

1 引言

平行板電容器模型如圖1所示.平行板電容器作為通交流阻直流的元器件，在電子線路以及生產和生活中應用非常普遍.在高中物理中，也經常碰到帶電粒子在平行板電容器間運動的問題.平行板電容器之間充滿均勻電場，處于其間的帶電粒子可以認為受到一個穩恒力的作用，因此帶電粒子的運動問題往往簡化為勻加速和勻減速的運動.從經典力學的角度，當帶電粒子的初始動能小于兩極板間的電勢差所帶來的電勢能U0，則帶電粒子不能到達右邊極板.但是經典力學只適用于宏觀粒子低速運動問題的求解.隨著進一步的學習，我們會逐漸接觸到納米器件，電容器作為基本元器件，其尺寸小到納米量級時，帶電粒子在其中的運動問題該如何求解，此時我們就需要引入量子力學方法[1,2].本文通過構建模型、構造勢壘、量子理論求解的方法分析了帶電粒子克服反向電場，穿透介觀平行板電容器問題，探究了平行板電容器通交流阻直流的特性受量子隧穿效應的影響.

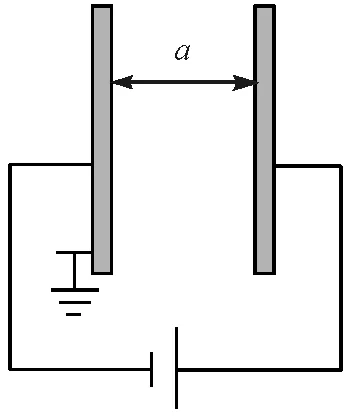
圖1 平行板電容器模型

2 理論模型和求解

如圖1所示，電容器的兩平行板之間的距離為a，電壓為V.考慮帶電量為+q的粒子從電容器的左極板入射，U0=qV為入射粒子在電容器兩極板上的電勢能差值.兩極板會給帶電粒子施加與運動方向相反的電場力，阻礙帶電粒子到達右極板.將粒子在整個一維空間的電勢能分為3個區域：Ⅰ區(x<0)，Ⅱ區(0≤x≤a)，Ⅲ區(x>a)，根據圖2所示的勢壘分布圖，電勢能的空間分布函數可表示為

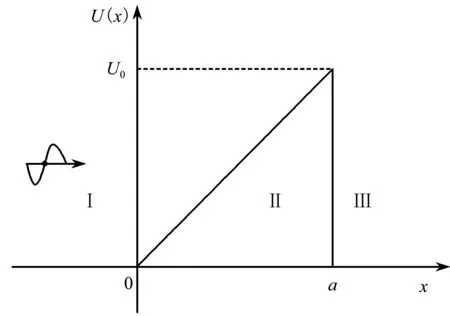
圖2 平行板電容器勢壘分布圖

(1)

(2)

式中m為帶電粒子的有效質量，?為普朗克常量，E為帶電粒子的本征能量，Ψ(x)為本征波函數.

在Ⅰ區和Ⅲ區，帶電粒子的波函數均滿足

(3)

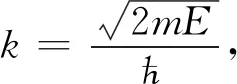
(4)

則Ⅰ區波函數的通解可表示為

ΨⅠ(x)=AⅠeikx+BⅠe-ikx

(5)

其中，AⅠ和BⅠ為待定系數，AⅠeikx表示帶電粒子的入射波函數，B1e-ikx表示帶電粒子的反射波函數.同理，Ⅲ區帶電粒子的波函數可表示為

ΨⅢ(x)=AⅢeikx

(6)

上式中AⅢ為Ⅲ區波函數的待定系數，波函數只包含AⅢeikx表示穿透平行板電容器后，帶電粒子在Ⅲ區不會再有反射，只能向右運動.

在Ⅱ區，帶電粒子的波函數滿足

(7)

(8)

上式為Airy方程[3,4]，其解為第一類艾里函數Ai(ξ)和第二類艾里函數Bi(ξ)的線性組合

ΨⅡ(ξ)=AⅡAi(ξ)+BⅡBi(ξ)

(9)

式中AⅡ和BⅡ為Ⅱ區帶電粒子波函數的待定系數.

隨后根據邊界條件求待定系數間的關系.波函數有兩個邊界，分別在x=0，x=a處.在x=0處，根據波函數及其一階導數連續，有

AⅠ+BⅠ=AⅡAi(ξⅠ)+BⅡBi(ξⅠ)

(10)

ikAⅠ-ikBⅠ=κAⅡAi′(ξⅠ)+κBⅡBi′(ξⅠ)

(11)

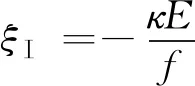
AⅢeika=AⅡAi(ξⅡ)+BⅡBi(ξⅡ)

(12)

ikAⅢeika=κAⅡAi′(ξⅡ)+κBⅡBi′(ξⅡ)

(13)

AⅠ+BⅠ=uAⅡ+σBⅡ

(14)

(15)

AⅢeika=cAⅡ+dBⅡ

(16)

(17)

利用ik乘以式(16)再減去式(17)得

(18)

上式中α=κc′-ikc，β=κc′-ikd.將式(18)代入式(17)得

(19)

上式中利用了艾里函數滿足的朗斯基行列式

2ikAⅠ=(iku+κu′)AⅡ+(ikσ+κσ′)BⅡ

(20)

式(18)代入式(20)得

(21)

將式(19)代入式(21)得

(22)

整理式(22)可得

(23)

由式(23)可得帶電粒子穿透電容器的透射系數

(24)

3 數值計算與分析

基于式(24)，下面通過數值求解畫出透射系數隨各種參數的變化情況.圖3(a)給出透射系數隨帶電粒子能量的變化，其中兩極板間電勢能的差值為U0=1.0 eV固定不變，板間距離a=1 nm.從左到右4條曲線對應的粒子質量分別為me,10me,100me,1 000me，me表示電子的靜止質量.各條曲線均表明即使帶電粒子的入射能量小于兩極板間的電勢能，帶電粒子也能克服反向電場力，穿透平行板電容器，平行板電容器通交流阻直流的效果在納米尺度是不成立的.隨著帶電粒子的入射能量的增強，其透射系數會不斷增加，當帶電粒子的能量E大于U0的3倍，透射系數接近1，對應基本所有的帶電粒子都能完全穿透平行板電容器.同時這里沒有共振隧穿現象，這是因為電容器勢壘不具有空間對稱性.對比4條曲線，還可發現在同一個橫坐標下，4條曲線的透射率大小不一樣，說明即使帶電粒子的動能不變，帶電粒子的透射系數還是會受到粒子質量的影響.

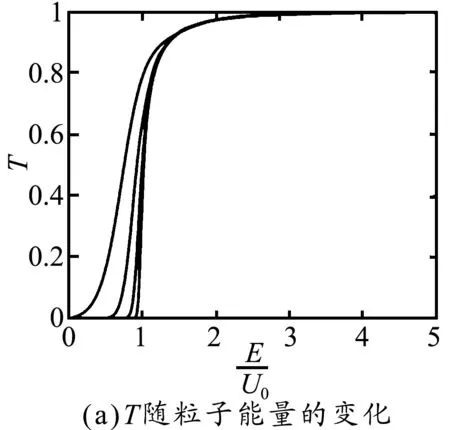
圖3 透射系數隨各量的變化

圖3(b)給出透射系數隨粒子質量的變化，其中板間距離a=1 nm，粒子的能量E0=1.0 eV固定不變，從上到下6條曲線分別對應U0=0.4E0，0.6E0，0.8E0，E0，1.1E0，1.2E0.圖中各條曲線顯示，隨著帶電粒子的質量變大，粒子的透射系數會不斷減小，直到趨近一個穩定的常數.該結果表明帶電粒子的動量大小會影響其透射系數，粒子動能不變的情況下，隨著粒子質量增加，其動量會減小，進而降低其透射幾率.同時發現U0≥E0的粒子的透射系數會趨近于零，U0

圖3(c)給出透射系數隨兩極板間勢能差值U0的變化，其中帶電粒子質量為me，粒子的入射能量E0=1.0 eV保持不變，從右到左4條曲線對應的電容器兩極板間的距離分別為1 nm，2 nm，10 nm，100 nm.每條曲線均表明隨著勢能差值的增加，透射系數會不斷減小，當勢能差值大于帶電粒子能量的3倍，透射系數接近零，對應基本沒有帶電粒子都能穿透平行板電容器.對比4條曲線，還可發現即使兩極板間電勢能的差值不變，當電容器兩極板間的距離增加，帶電粒子的透射系數還是會不斷減小，此時對應電容器勢壘的寬度變寬了，更難被跨越.當兩極板間的距離非常大，達到100 nm，此時小于勢壘能量的帶電粒子基本不會發生透射.

圖3(d)給出透射系數隨兩極板間距離a的變化，其中帶電粒子質量為me，E0=1.0 eV，從上到下6條曲線分別對應U0=0.4E0，0.6E0，0.8E0，E0，1.1E0，1.2E0，每條曲線都顯示隨著兩極板間的距離的變大，透射系數有減小的趨勢.在透射系數減小的過程中，其實不是單調遞減，而是會出現波浪形振蕩的減小，這體現了微觀粒子的波粒二象性.更具體的，可發現隨著兩極板間的距離的變大，U0≥E0的粒子的透射系數會趨近于零，U0

4結論

本文探討帶電粒子克服勢壘穿透單個介觀平行板電容器的問題，發現即使帶電粒子的入射能量小于兩極板間的電勢能，帶電粒子也能克服反向電場力，穿透平行板電容器.隨著帶電粒子的入射能量的增強，其透射系數會不斷增加.在入射能量不變的情況下，增加反向電壓、增加粒子質量、增加兩極板間的距離等因素都會降低帶電粒子的透射系數.上述結果表明量子隧穿效應對納米元器件的性能影響很大,平行板電容器通交流阻直流的效果在納米尺度是難以實現的，就算帶電粒子的入射能量小于兩極板間的電勢能,也需電容器兩極板的距離大于100 nm以上，此時其阻直流的效果才會比較明顯.