節點剛接與螺栓連接的屈曲約束支撐框架結構抗震性能

虞愛平， 劉祥泰， 毛飛騰， 王翠紅， 鄧雪蓮*

(1.廣西巖土力學與工程重點實驗室， 桂林 541000； 2.桂林理工大學土木與建筑工程學院， 桂林 541000)

設計合理的屈曲約束支撐(buckling restrained braced，BRB)在拉、壓作用下均可進入屈服耗能，使鋼支撐的受壓強度和耗能能力得到充分利用，具有穩定的滯回耗能能力和較大的延性[1]，將此類支撐布置在框架層間形成了屈曲約束支撐框架(buckling restrained braced frame，BRBF)結構體系，在工程結構中得到了廣泛應用。中外學者對其進行了各類研究[2-4]。王永貴等[5]在5種工況下的抗側剛度比及兩種布置方式下，對3種不同層數的結構模型進行彈塑性靜力分析，研究表明抗側剛度比較支撐布置方式對屈曲約束支撐鋼框架結構抗震性能的影響更為顯著；陳宜虎等[6]采用兩種多層BRBF典型結構形式模型為研究對象，以各模型的BRB水平力分擔率平均值和首層剪重比為主要研究參數，探討了多層BRBF結構抗震性能；胡俊等[7]對不同有效屈服長度比的長行程的BRB進行了擬靜力試驗。研究發現高有效屈服長度比能夠有效提高試件的極限承載力及位移且強度穩定退化，而有效屈服長度比對長行程BRB的剛度退化性能影響不大；杜志強等[8]提出了一種新型BRB消能器，且不需要填充混凝土，更易于裝配、檢視和更換。然而比傳統BRB重量更大才能達到相同的耗能能力；殷占忠等[9]對原框架和增設改進型雙鋼管約束屈曲支撐加固的鋼框架進行了Pushover分析和非線性時程分析，發現改進型雙鋼管約束屈曲支撐框架的剛度和強度明顯提高，可提高結構的抗震性能；賀強等[10]研究了帶BRB的扭轉不規則框架，在罕遇地震作用下的扭轉位移比變化均勻，最大值為1.17。框架底層BRB滯回曲線飽滿，耗能減震效果明顯。

在地震作用下，鋼結構整體倒塌破壞發生較少，主要發生在梁柱節點區域，其中節點區域的焊接應用最廣，靈活性好，但易變形，焊縫附近材質加熱升溫變脆，效率低等缺點。近年來，梁柱節點采用螺栓連接的形式減少了現場焊接施工污染，且具有震后修復簡單，人工成本少，效率提高等優點。

綜上所述，深入研究不同梁柱節點連接形式的鋼框架結構的抗震性能對鋼結構形式發展具有重要意義。為此，通過節點轉換將原梁柱節點剛接的BRBF模型轉變成節點螺栓連接的BRBF模型，然后通過CLAP軟件對兩種BRBF模型進行靜動力分析。

1 分析模型

1.1 模型參數

中國鋼結構跨度常用的有6～24 m，并結合傳統的民用建筑的層高3～4.5 m，以8層梁柱節點剛接的屈曲約束支撐鋼框架(T-BRBF，簡稱TM)模型和8層梁柱節點螺栓連接的屈曲約束支撐鋼框架(S-BRBF，簡稱SM)模型為研究對象。設計4榀3跨的對稱正方形鋼框架結構，各跨跨度均為7.2 m，總跨度為21.6 m，框架首層層高4.5 m，其他層高4.0 m，總高度為32.5 m。模型柱采用箱型鋼柱，梁采用H型鋼，梁和柱的鋼材采用Q355鋼材。BRB的芯材采用實心方形鋼棒，采用Q235鋼材。BRBF模型的柱腳剛接，BRB兩端與梁柱節點鉸接。BRB支撐形式設計成“K”字形。材料彈性模量E=20 500 N/mm2，剪切模量G=7 900 N/mm2。

根據日本的BRBF結構設計，建議柱梁剛接框架中BRB的β值為30%左右[11]，因此將3組基本模型的BRB水平分擔率β值分別設置為20%、30%、40%，并將TM模型分別命名為TM20、TM30、TM40。通過節點轉換[12]將TM模型轉變成節SM模型，對應命名為SM20、SM30、SM40。由于BRBF模型對稱分布，故取Y1、Y2榀框架作為研究對象，BRBF模型平面及立面圖如圖1所示。

根據文獻[13]，BRB在框架中承擔水平剪力所占比例用支撐水平力分擔率β定義，其計算公式為

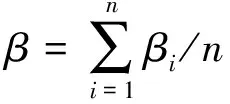
(1)

βi=Qbui/Qui

(2)

式中：βi為第i層BRB水平力分擔率；Qbui為達到設計層剪力時第i層BRB分擔的水平剪力；Qui為第i層的設計層剪力；n為模型層數。

C1、C2分別為邊柱、角柱；B為框架梁圖1 框架模型Fig.1 Frame model

結合CLAP軟件，調整梁、柱截面，使得層定義下強柱系數控制在2.3，控制框架基本周期較為接近。各模型第i層強柱系數αi的表達式為

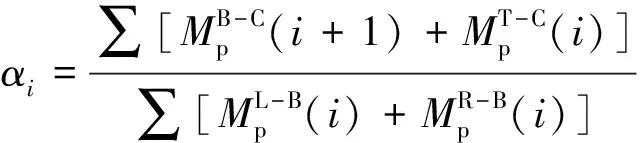
(3)

2 靜力彈塑性分析

2.1 分析方法

(1)分析軟件：運用CLAP軟件基于位移控制(即位移增分法)對模型進行靜力推覆分析，總計100增份。

(2)分析建模：計算模型圖如圖1所示。假定屈服后的材料剛度為1/100的初始剛度。考慮模型中各榀框架的對稱性且樓板剛度較大，假設各層樓板均為剛性，對各模型僅選取外兩榀框架(即Y1榀和Y2榀)進行靜力推覆分析。

(3)荷載布置：地震分布的水平荷載采用倒三角分布豎向集中作用在每一層的柱頂，用T1表示，地震作用等效水平荷載作用于各層柱柱頭，對應于每層用F1～F8表示，圖2為分析模型各層的受力形式。

(4)構件恢復力模型：框架柱梁鋼材本構關系采用雙線型。

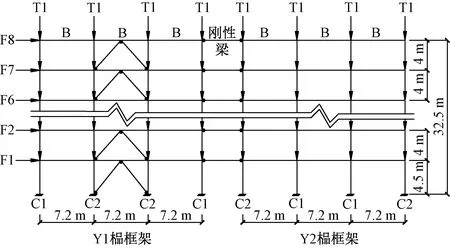
圖2 分析模型荷載分布Fig.2 Load distribution of analysis model

2.2 結果分析

2.2.1 層剪力和層間位移的關系

圖3、圖4為靜力彈塑性分析中各模型層剪力Q與層間位移U關系曲線(Q-U關系曲線)，并繪出達到彈性層間位移角限值1/250和彈塑性層間位移角限值1/50(失效點)時和BRB、梁初次形成塑性鉸時各層剪力與位移關系。表1為6組模型達到1/50(失效點)時的主要變化參數。

圖3 模型T-BRBF的層剪力與層間位移關系曲線Fig.3 Relationship between story shear and inter-story displacement of model T-BRBF

由圖3、圖4可知，各層構件首次出現塑性鉸的順序為：BRB 屈服→結構達到彈性層間位移角限值 1/250→梁端屈服→結構達到層間位移角限值 1/50。

對比3個TM模型，在達到彈性層間位移角限值1/250以及梁出現塑性鉸時，Q-U關系曲線及變化幅值區別不大，而主要區別在于BRB的層剪力及層間位移隨著β值的增大而增大，符合增大β值后的效果。其次模型TM20、TM30、TM40達到失效點1/50時，首層最大層剪力破壞分別為10 000、9 500、9 700 kN，而頂層最大層剪力破壞分別為3 200、3 000、3 100 kN，最大層間位移分別在3、4、3層，均集中在中下部樓層且突出明顯。

圖4 模型S-BRBF的層剪力與層間位移關系曲線Fig.4 Relationship between story shear and inter-story displacement of Model S-BRBF

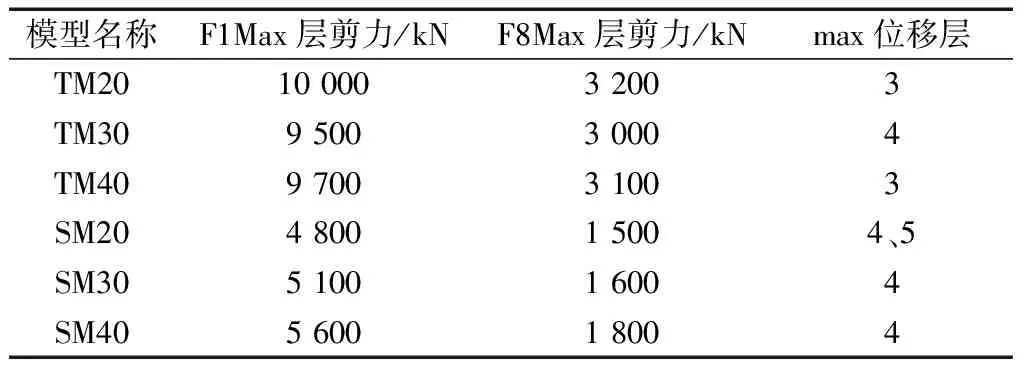
表1 模型達到失效點1/50時的主要變化參數

對比3個SM模型，模型SM30的Q-U關系曲線與模型SM20相似。而模型SM40與模型SM20和SM30相比，達到彈性層間位移角限值1/250時，BRB、梁端和達到失效點1/50時首次出現塑性鉸的各層層剪力持續增加，框架層間位移整體小幅度增加。模型SM20、SM30、SM40達到失效點1/50時，首層最大層剪力破壞分別在4 800 、5 100 、5 600 kN，而頂層最大層剪力破壞分別在1 500、1 600、1 800 kN，最大層間位移分別在4.5、4、4層，均集中在中下部樓層且突出明顯。

綜上所述，在相同β值下，梁柱節點從剛性連接改為螺栓連接后，結構首層和頂層失效時的最大破壞層剪力降低了1/2。在推覆分析過程中，伴隨著β值增大，不同連接方式的結構整體層剪力均隨著β值增大而增大。達到彈塑性層間位移角限值1/50時，兩種不同連接方式的BRBF結構均表現出中下部或者中部樓層變形突出的特征，但總體而言SM模型的最大變形樓層集中上移。

3 動力彈塑性分析

3.1 地震波選擇

假定結構阻尼系數為2%的剛度比例型，研究模型采用抗震設防烈度為8°、9°，所對應的峰值加速度分別設為400、620 cm/s2。地震分組取第二組，場地類別為Ⅱ類，框架抗震等級為二級。各模型動力時程分析時間為30 s，時間間隔為0.01 s。根據《建筑抗震設計規范》(GB 50011—2010)[14]以及地震的不確定性，為了使平均地震影響系數曲線應與反應譜曲線在統計意義上相符，應選取不少于兩組的實際強震記錄和一組人工模擬記錄進行彈性時程分析法。因此，選擇7條反應譜平均值與抗震規范中建筑結構地震影響系數(反應譜)曲線相吻合的地震波，其中影響系數曲線如圖5所示。包括兩條人工波：ART1、ART2和5條天然波CHICHI、HM、IWATE、TCU、TH4，其中天然波占比大于2/3。

3.2 分析結果

3.2.1 最大層間位移分布

β值為20%、30%、40%的各模型在兩種不同加速度峰值的罕遇地震作用下各層最大層間位移關系如圖6所示，并在圖6中加入1/250、1/100、1/50的層間位移角參考線。6個模型在不同加速度峰值荷載作用下位移值及位移差如表2所示。根據圖6及表2分析得出如下結論。

(1)各組模型的層間位移均控制在彈塑性層間位移角限值1/50以內，幾乎都大于彈性層間位移角1/250。變化規律都呈現先增大后減小的規律，在2～6層，SM模型層間位移均明顯大于TM模型，結構整體變形更為嚴重，表明SM模型在地震作用下抗側移性能較差，TM模型整體相對穩定。

(2)加速度峰值為400 cm/s2時，兩個模型都控制1/250～1/100。模型TM20和模型SM20的最大層間位移都出現在第2層，最大層間位移值接近，分別為3.44、3.47 cm，相差近0.03 cm。TM30模型和SM30模型最大層間位移在第5層，分別3.09、3.41 cm，相差近0.32 cm。TM40、SM40模型最大層間位移分別出現在第2層(2.98 cm)、第3層(3.50 cm)，相差近0.52 cm。可見，不同β值的同種連接形式模型結構整體的最大層間位移接近，但最大位移差隨著β值增加而不斷增大。

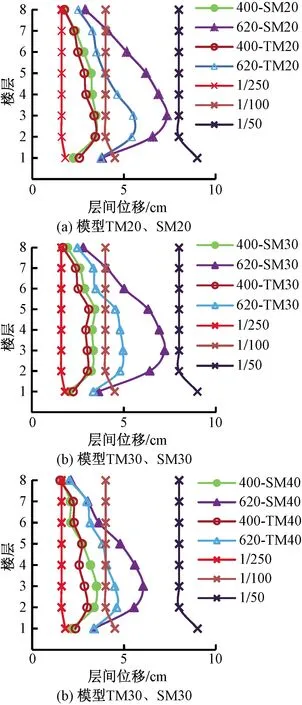
圖6 最大層間位移分布Fig.6 Maximum layer displacement distribution

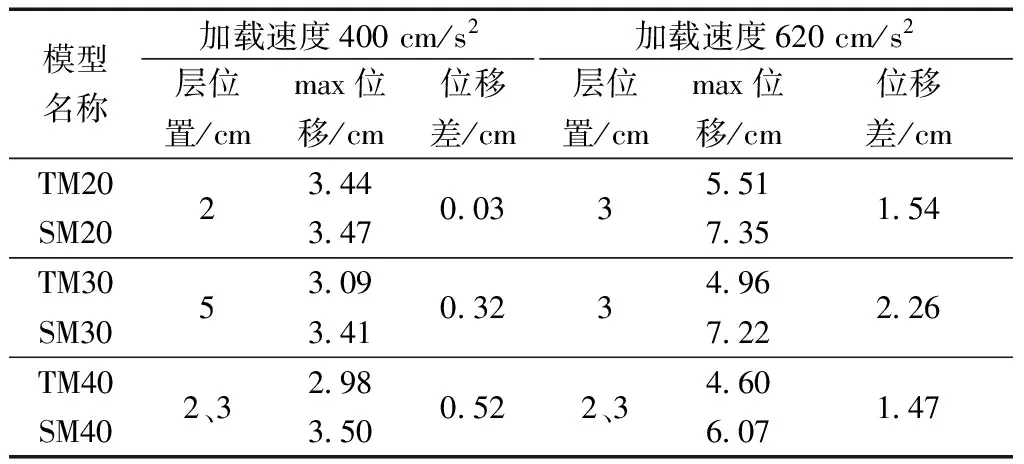
表2 不同連接方式的不同加速度荷載峰值作用下的 Max位移值及位移差

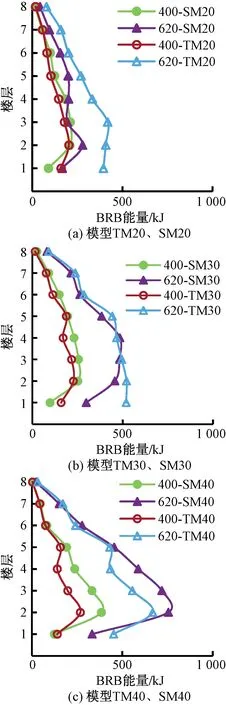
圖7 各模型各層 BRB 吸收的塑性能量分布Fig.7 The plastic energy distribution of layers BRB sharing

(3)在加速度峰值為620 cm/s2時，β=20%和β=30%的模型層間位移區別不明顯，而β=40%的模型則整體明顯減小。SM模型局部層變形突出現象更明顯。TM20、SM20、TM30、SM30、TM40、SM40模型的最大層間位移分別為5.51(第3層)、7.35(第3層)、4.96(第3層)、7.22(第3層)、4.60 (第2層)、6.07 cm(第3層)，相差近1.54、2.26、1.47 cm。

3.2.2 BRB塑性變形能量分布

各模型在兩種不同加速度峰值的罕遇地震作用下的BRB能量如圖7所示。隨著樓層的增加，不論是TM模型還是SM模型，BRB吸收塑性變形能量總體呈現先增大后減少的趨勢。除了在加速度峰值為620 cm/s2時，模型TM20的BRB能量明顯比模型SM20大，其余在同種加速度峰值下，TM模型與SM模型中BRB吸收塑性變形能量基本相差不大。模型SM20和TM20的各層BRB吸收塑性變形能量值變化相對緩和，都在中下層集中。模型TM30和SM30的BRB能量主要集中在出現在2～4層，模型TM40和SM40的BRB能量主要集中在2層，且集中現象明顯。

綜上，隨著β值的增大，不論是TM模型還是SM模型，其BRB吸收塑性變形能量值越往下部層集中，易出現損傷集中效應和變形在某些層增大，而其他層難以變形的不利現象。

3.2.3 彈塑性分析層滯回曲線關系

根據對模型彈塑性能量分布的統計分析，得知在加速度峰值為400 cm/s2地震作用下，模型TM組和模型SM組中吸收的全部塑性應變能量Ep最大的模型為TM30和SM30，且最大層能量對應為第二層和第三層。在模型TM30中吸收塑性應變能量最大的構件為2層的右側BRB，模型SM30的3層右側BRB。在加速度峰值為620 cm/s2的地震作用下，吸收塑性應變能量最大的構件則為模型TM30的2層的左側BRB和模型SM30的3層右側BRB。選擇這4個構件滯回曲線進行分析，如圖8所示。

圖8 TM30模型和SM30模型的BRB滯回曲線Fig.8 BRB hysteretic curves of TM30 model and SM30 model

對比圖8(a)和圖8(c)、圖8(b)和圖8(d)可知，從整體趨勢來看，模型耗能最大的構件BRB的滯回曲線都比較飽滿。滯回曲線面積隨著加速度峰值增加而變大，模型SM30增大尤為明顯，說明構件耗能增加，符合增加加速度峰值后的效果。對比圖8(a)和圖8(b)、圖8(c)和圖8(d)可知，在加速度峰值為400 cm/s2時，模型TM30的變形范圍在-1～2.5 cm，在-1～1.5 cm滯回次數最多，模型SM30則為-2～2 cm，在-1～1 cm滯回次數最多，但是兩個模型的滯回曲線面積相近。在加速度峰值為620 cm/s2時，兩個模型的滯回曲線面積存在較大差異，模型TM30的變形范圍為-3～2 cm，循環次數多且集中，而模型SM30的變形范圍為-3～8 cm，但梁柱節點采用螺栓連接的BRBF模型的地震需求耗能更多。

4 結論

(1)梁柱節點從剛性連接改為螺栓連接后，結構首層和頂層失效時的最大破壞層剪力降低了1/2，這是因為螺栓連接模型的剛度較剛接模型低。其次達到彈塑性層間位移角限值1/50時，兩種不同連接方式的BRBF結構均表現出中下部樓層變形突出的特征。

(2)在地震波作用下，各組模型的層間位移均控制在彈塑性層間位移角限值1/50以內，幾乎都大于彈性層間位移角1/250，都呈現先增大后減小的規律。梁柱節點螺栓連接模型層間位移均明顯大于剛接模型，說明剛接模型抗側移能力更強。

(3)除在加速度峰值為620 cm/s2時，模型TM20的BRB能量明顯比模型SM20大，其余在同種加速度峰值下，模型TM與模型SM中BRB吸收塑性變形能量基本相差不大，且都往中下部層集中現象。

(4)滯回曲線飽滿，但梁柱節點螺栓連接的模型的滯回曲線面積大于剛接模型，地震需求耗能更多。