周期性尾跡對渦輪端區二次流強度影響

曹惠玲， 左燦林

(中國民航大學航空工程學院， 天津 300300)

低壓渦輪是現代渦扇發動機的主要部件，對其內部三維流場結構的研究具有重要的意義[1-2]隨著航空業的發展，渦輪減重成為渦扇發動機設計的一個關鍵問題，而通過增加葉型的氣動載荷來減少低壓渦輪葉片的數量是減輕渦輪重量的同時提高渦輪性能的有效途徑。Opoka[3]指出低壓渦輪中二次流損失占據了總損失極大一部分，且柵距增加的同時會為二次流提供更大的發展空間。Cui 等[4]借助大渦模擬對高負荷低壓渦輪葉型 T106A進行了端區流動模擬，研究尾跡對端區流動造成的影響，并指出來流尾跡能有效地抑制分離泡的發展。為保證渦輪在進行減重的同時盡可能減少端區損失占比，如改變葉片前緣構型及改變端壁構型等方法可有效對端區流動進行改善[5-6]。

中外學者針對的端區流動做了一系列的數值模擬和實驗研究。Benner等[7]借助油流實驗和七孔探針明確了端區附面層的發展和遷移路徑，并且將端區渦系結構的形成及發展規律進行了細化研究。Marks等[8]采用粒子圖像測速法(particle image velocimetry, PIV)技術對高負荷低壓渦輪端區二次流進行了詳細測量，給出了低壓渦輪端區二次流結構模型。Cui等[9]研究了上游尾跡對端區流動結構造成的影響，并對低壓渦輪端區二次流結構模型進行了改進。

葉輪機械內部流場存在的周期性非定常特性使得定常工況下端區二次流模型結構無法完全正確反映渦輪內部真實流動情況，在真實發動機工作過程中，上游尾跡的存在是不可避免的流動現象，并會對端區流動產生周期性的影響變化[10]。Schneider等[11]采用數值與實驗相互結合的方法對低壓渦輪端區流動進行了研究，并證明了上游通道渦和尾跡進入下游葉柵通道后會產生強烈的非定常作用，使端區通道渦的強度顯著降低。Ciorciari 等[12]在進行非定常實驗和數值研究中得出了相似的結論，并在研究過程中發現端區二次流渦結構強度會伴隨著尾跡掃掠頻率的增大而減弱。Murawski等[13]認為進口氣流角的動態變化會影響端區二次流的發展以及尾跡掃掠頻率會影響到二次流結構的穩定性。Satta等[14]借助實驗方法對定常與非定常工況下高負荷低壓渦輪端區進行了研究，結果表明上游尾跡的存在可明顯降低二次流損失，且工作雷諾數越高尾跡對端區二次流的抑制效果更好。

上述學者對于上游尾跡及端區流動之間進行了大量的研究，并采用平面葉柵實驗臺對其流動特性進行了相應研究，但對在尾跡作用下端區流動結構及端區流動損失變化影響機理研究的論述較少。因此本文希望以上游尾跡對端區附面層所產生的影響以及尾跡對通道內部渦系結構的影響機理作為研究點，借助更為接近真實渦輪內部真實流動的扇形葉柵風洞實驗臺，分析上游尾跡對端區流動發展的影響。研究過程中采用上游圓棒圓柱繞流的方式來模擬非定常工況尾跡的形成，并使用典型高負荷低壓渦輪Packb葉型作為研究對象，來流條件設置為雷諾數Re=115 000，來流湍流度FSTI=1.5%、流量系數Ф=1.0、折合頻率Fr=1.128，對尾跡造成的端區流動影響進行數值與實驗研究，并對其流動影響機理進行分析。

1 數值方法與實驗驗證

1.1 數值模擬方法

為保證仿真計算的精度，采用商用計算流體力學(computational fluid dynamics,CFD)軟件ANSYS-CFX 2020R1進行數值模擬仿真，并借助LES作為瞬態模擬進行計算，使用實驗數據結果進行驗證。在使用LES模型時需要借助Smagorinsky亞格子應力模型來模擬亞格子尺度的脈動。同時在Smagorinsky亞格子模型的基礎上使用Van-Driest壁面函數來彌補近端壁處及前尾緣處的湍動能耗散，其中函數系數設置為默認的25，亞格子模型常數設置為0.1，空間項離項和時間項離散分別選取為Central Difference和Second Order Backward Euler，根據Funazaki 等[15]的研究結果，在這種求解設置下能夠對高負荷低壓渦輪端壁二次流流動進行準確模擬。

計算域高度采用半葉高，研究表明高負荷Packb葉型端區二次流影響范圍在30%葉高以下，采用半葉高簡化計算域可以在減少計算量的同時不會對端區流動產生較大的影響，可以準確地反映端區二次流流動特性。表1為Packb葉型參數及工況條件，圖1為帶圓棒的葉柵通道計算域拓撲示意圖及前尾緣網格模型圖。圖1中，軸向弦長設置為Cx，h為葉片高度，上游圓棒距葉片前緣的軸向距離為0.6Cx，氣流進口平面至圓棒的軸向長度距離為 0.6Cx，氣流出口平面距葉片尾緣的軸向距離為Cx，相鄰葉柵通道圓棒之間設置為一個柵距，全環葉柵流道中葉片數為50，因此在進行單個葉片通道劃分時計算域的范圍為7.2°。在進行網格劃分時，對環繞葉片近壁面區域一周的區域以及圓棒進行“O”形網格切分，其余區域設置為“H”形網格切分。為確保在雷諾數Re=115 000的工況下近輪轂端壁處及圓棒處y+<1,葉片前尾緣處y+<1.4,葉片外緣區域y+<1.2,將環繞葉片近壁面一周的節點數設置為620，x軸軸向上節點數設置為551，y軸環向上設置節點數為211，z軸展向上設置131個節點，葉片壁面第一層網格高度最大為0.015 mm,端壁壁面法向第一層網格最大高度為0.010 mm，上游圓棒計算域內總節點數控制在85×104左右，計算域總網格數約為1 450×104。

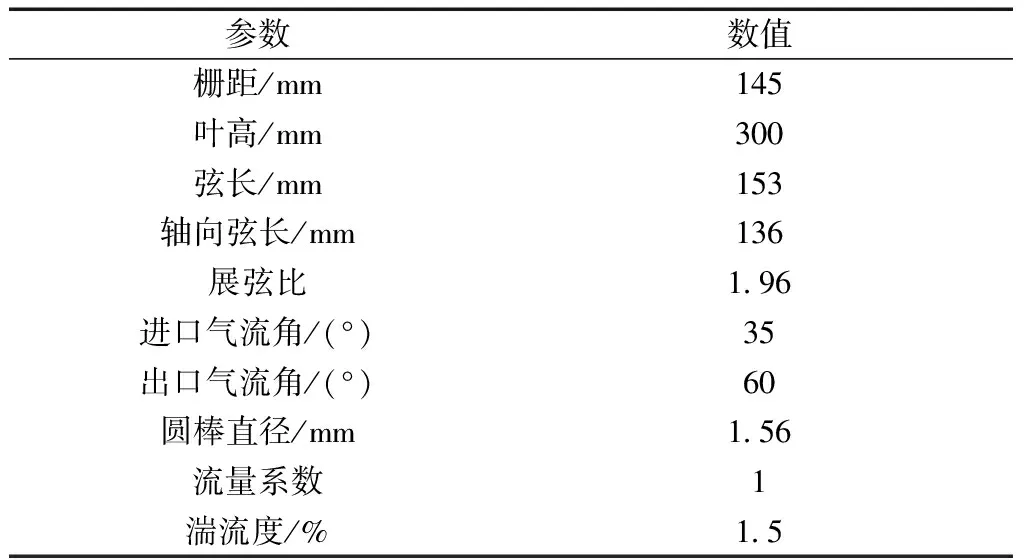
表1 Packb葉型主要參數

h為計算域高度圖1 計算域劃分Fig.1 View of computational domain

流量系數Ф定義為

(1)

式(1)中：Ux為葉柵軸向速度；Ub為尾跡發生器圓棒線速度。

折合頻率Fr定義為

(2)

式(2)中：Cx為軸向弦長；Cy為葉柵柵距。

1.2 實驗驗證

實驗研究借助于低速扇形葉柵風洞實驗臺，圖2為該試驗臺的整體示意圖，由離心風機、擴張段、穩流段、收縮段、試驗段構成，研究表明在相同工況條件下，葉片與圓棒掃掠形成的上游尾跡結構相同，故采用尾跡發生器掃掠來模擬尾跡生成。借助光電轉速傳感器用以監控圓棒轉速從而實現與熱膜信號的同步，在45%葉高處設置有靜壓孔并使用DSA 3217傳感器進行壁面靜壓測量，柵后及端壁流場則借助于7孔探針。

圖2 實驗裝置Fig.2 Experimental setup

為驗證數值模擬的準確性，采用壓力系數及出口處總壓損失系數云圖進行驗證，其中載荷系數定義為

(3)

總壓損失系數定義為

(4)

式中：下標in為進口參數；下標out為出口參數；下標local為測試處參數；下標0為總壓，用出口動壓進行無量綱處理。

圖3為數值模擬與實驗數據的靜壓系數對比，取45%葉高處葉片吸力面和壓力面壓力系數作為對照依據，表明數值模擬與實驗結果基本相符，平臺及載荷峰值點位置吻合程度較好，可認為數值模擬結果具有可靠性。

圖4為葉片尾緣即x=1.0Cx處總壓損失系數云圖。可以看出實驗結果與CFD計算結果基本吻合，其渦系結構所代表的損失大小在圖4中可得到很好體現。

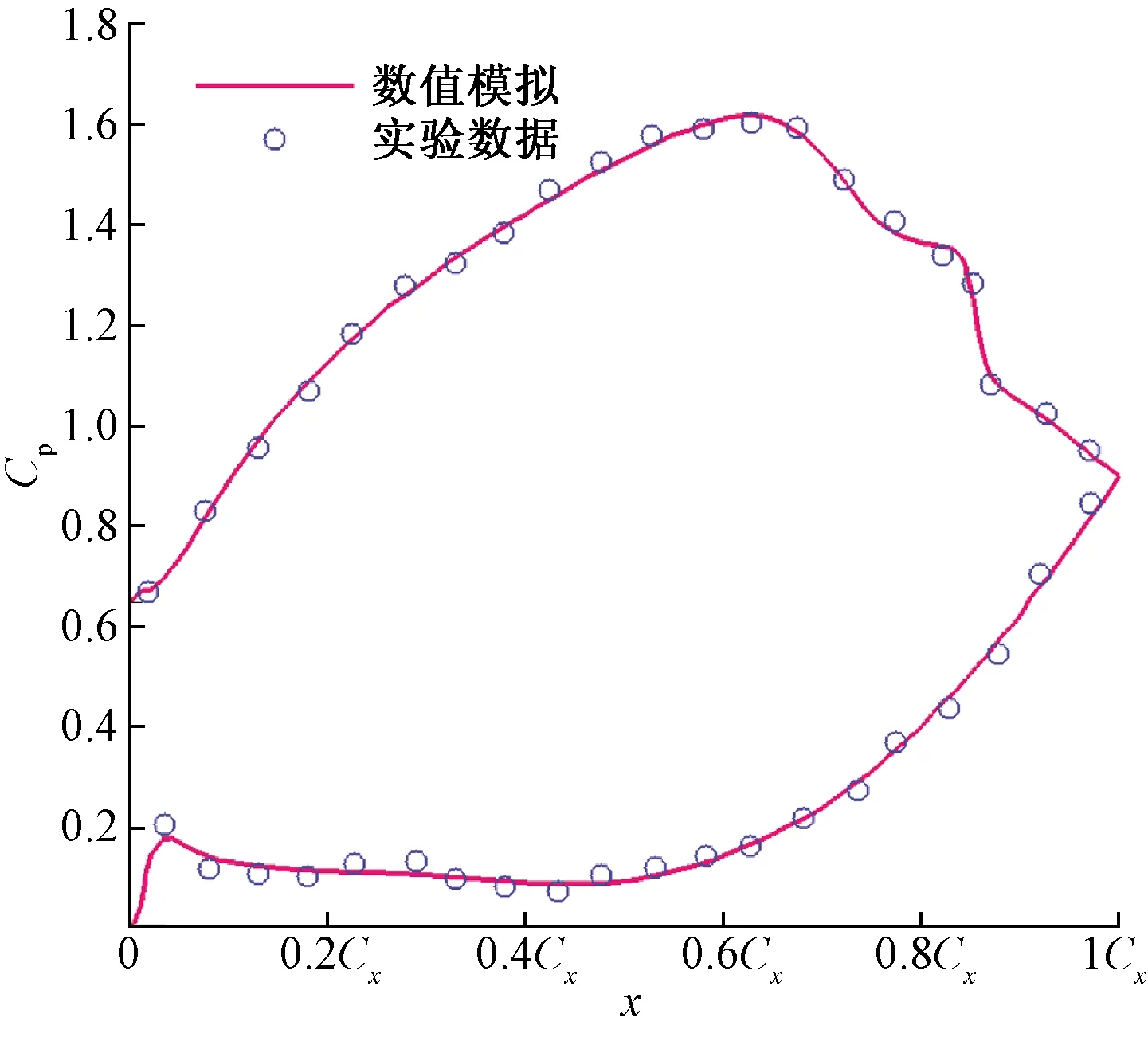
x為軸向位置圖3 45%葉高處靜壓系數分布Fig.3 Static pressure coefficient distribution at 45% span

θ為葉柵通道環向坐標無量綱數值圖4 出口處總壓損失系數分布Fig.4 Total pressure loss coefficient distribution at exit

2 結果與討論

2.1 定常工況結果分析

圖5為葉柵通道出口處使用Q準則識別出的渦系結構。由于識別出的渦結構具有矢量特征，故將其分為流向渦、徑向渦以及法向渦。圖5可根據渦量大小明顯識別出通道渦以及發展過程中誘導而出的對渦，可以看出這與Cui等[9]提出的低壓渦輪典型二次流結構基本對應。其中通道渦主要由橫向壓力梯度推動形成，定義為流向渦，是端壁主要的二次流結構，會對端區損失的大小產生重要影響。

2.2 非定常工況結果分析

圖6為定常與非定常數值計算葉柵進口處速度型和尾緣處總壓損失系數在一周期內時均結果對比圖。從圖6(a)可以看出，尾跡由于負射流效應對速度進行了一定的削減，但對附面層的厚度未產生較大影響，可認為尾跡通過附面層厚度去對二次流強度產生的影響程度較小。在圖6(b)中可觀測到，尾跡的存在使0.2h葉高之上葉中區域總壓損失顯著減少，通道渦處局部高損區基本未受太大影響，僅核心位置略有下移，這使得端壁附近所占損失比重上升。非定常計算結果進行時均數據處理后，雖對出口平面處總壓損失的大小進行了很好的比對，但失去了許多瞬態變化的過程，無法從時均結果中觀察到壁面渦結構造成的局部高損區及通道渦對主流附面層產生的影響，因此在后文將對瞬態結果進行詳細分析。

圖7為一個尾跡掃掠周期內不同時刻尾緣下游0.15Cx處(x=1.15Cx)的總壓損失分布情況。可以看出，通道渦在徑向位置上基本未發生變化，但通道渦所在損失區大小產生了較大周期性的變化。在尾跡周期初期t/T=0.1～0.4時刻通道渦大小存在明顯增大趨勢，在該時段內尾跡尾部從壓力面逐漸朝吸力面進行運輸，且通道渦尺度大于定常無尾跡工況通道渦的尺度。t/T=0.4時刻尾跡尾部恰好與吸力面完全接觸，此時通道渦尺度范圍達到最大，在這一階段尾跡遷移過程中會將端壁附近附面層及低能流體卷起抬升從而加強了通道渦強度與影響范圍。

圖5 出口處渦系結構Fig.5 Vortex structure at exit

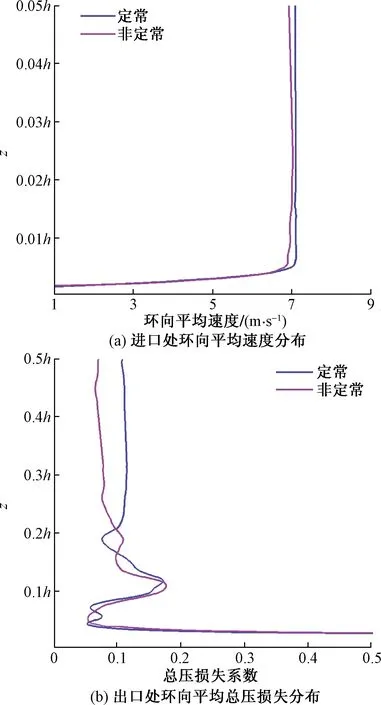
圖6 進出口參數分布Fig.6 Distribution of inlet and outlet parameters

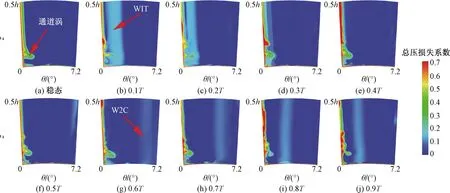
t為所處時刻；T為尾跡周期；W1T為第一條尾跡尾部；W2C為第二條尾跡中心圖7 尾緣下游0.15Cx處總壓損失瞬態分布Fig.7 Total pressure loss at 0.15Cx downstream of trailing edge

t/T=0.5～0.9時段內第二條尾跡中心進入葉柵通道并從吸力面向壓力面運動，但其并未與吸力面接觸。該時段內尾跡中心對馬蹄渦結構進行破壞使其破碎，破碎后的馬蹄渦被輸送至葉柵出口處降低通道渦強度，使通道渦大小呈現出削減趨勢。t/T=0.9時刻通道渦大小達到一個最低值且顯著低于無尾跡下的通道渦尺度。從兩個時間段內的通道渦尺度變化趨勢可得出尾跡對通道渦強度存在增強與削弱作用，其增強與削弱作用周期性交替出現的原因是尾跡在通道中所處位置不同所造成的。

2.3 尾跡對馬蹄渦周期性削弱作用

為進一步研究尾跡對馬蹄渦的周期性削弱作用的影響機理，圖8為不同時刻不同截面處馬蹄渦、通道渦及尾跡遷移演化過程，分別從葉柵前緣進口處及尾緣出口處進行觀測，其中W1、W2、W3分別為尾跡1、尾跡2、尾跡3。截面分別處于x/Cx=0.4、x/Cx=0.5，x/Cx=0.6、x/Cx=0.7、x/Cx=0.8、x/Cx=0.9、x/Cx=1.0位置，主要從后4個截面對流動進行分析描述。

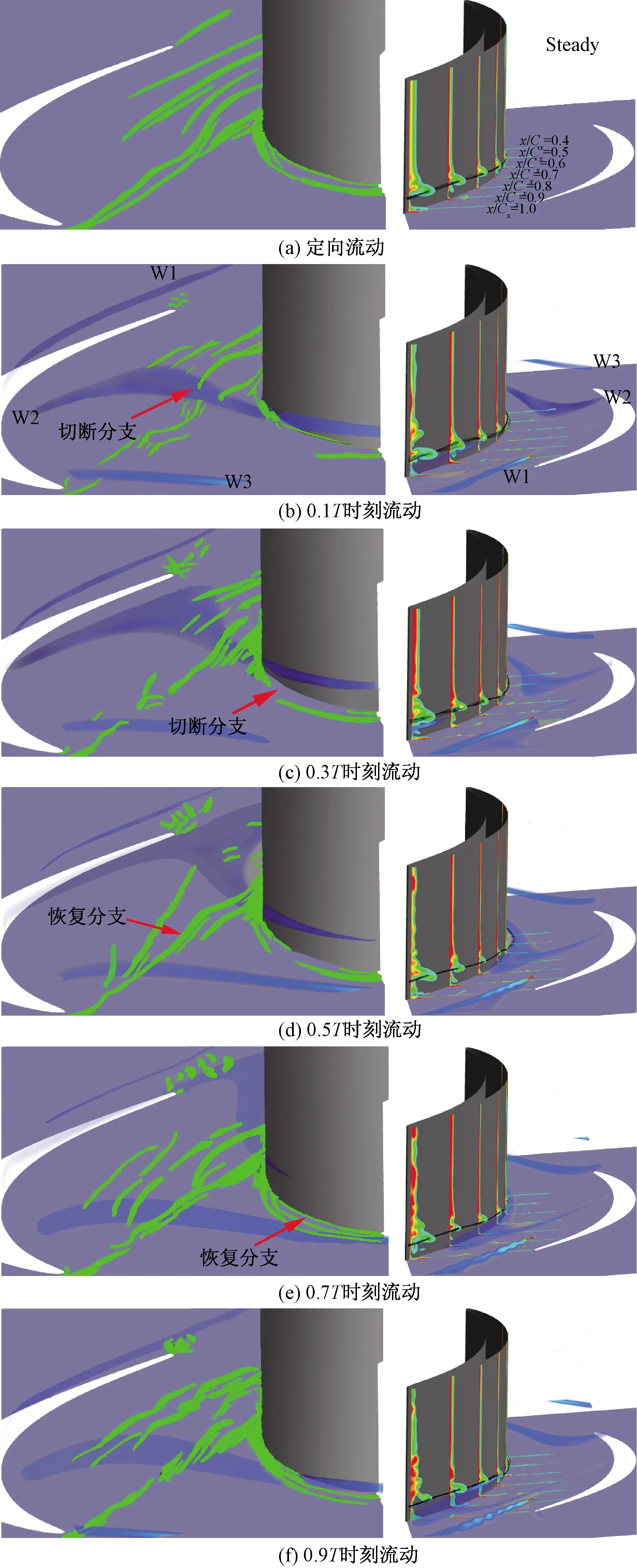
左側綠色渦結構為使用Q準則識別而出的馬蹄渦吸壓力面分支；右 側為葉柵通道內不同截面處的總壓損失；淡藍色透明帶為尾跡形態圖8 端壁瞬態流動Fig.8 Instantaneous flow at endwall region

在尾跡周期初期t/T=0.1的時刻W2、W3尾跡與馬蹄渦壓力面分支接觸并使其破碎，未形成完整的馬蹄渦結構。t/T=0.3的時刻，尾跡繼續向下游遷移，W2尾跡同時從壓力面向吸力面靠攏，馬蹄渦吸力面分支在與尾跡接觸后同樣被其切斷破壞，由于橫向壓力梯度的影響使得尾跡先破壞壓力面分支后破碎吸力面分支，此時兩者強度都被尾跡進行了削弱。在t/T=0.5時刻W2尾跡遷移至葉柵通道中下游部分區域。

馬蹄渦的壓力面分支依然是破碎的，在此時馬蹄渦的吸力面分支也被抑制。圓棒運動方向為從壓力面一側逐漸轉向吸力面一側，因此尾跡對馬蹄渦分支的抑制作用有先后的順序，即先切斷并抑制了馬蹄渦的壓力面分支，之后又破壞并抑制了馬蹄渦的吸力面分支。在t/T=0.5時刻，尾跡運輸到了葉柵通道的中后部，此時通道內壓力面分支恢復原狀，且吸力面分支也具有恢復的趨勢。在t/T=0.7時刻吸力面分支完全恢復，t/T=0.9時刻吸壓力面分支都較為完整。與定常狀況下渦結構相比，非定常下葉柵通道內分支數量及完整程度都有所差距，這是由于尾跡的剪切作用使得的馬蹄渦結構不完整所造成的。在尾跡向下游運輸后，馬蹄渦的吸壓力面分支存在恢復趨勢，但是仍然無法恢復到無尾跡下渦結構的完整程度及強度，如果增大尾跡的掃掠頻率可以預測馬蹄渦的破碎程度將加劇。

值得注意的是，因為馬蹄渦的吸壓力面分支是通道渦的起源，當馬蹄渦分支被抑制時，會導致通道渦的尺度發生明顯變化。但是由于馬蹄渦吸壓力面分支運輸至出口處的通道渦并融合存在時間上的延遲，所以在一個周期初期以及尾跡切碎馬蹄渦吸壓力面分支的時刻無法觀測到通道渦尺度及出口處損失減小的現象。而是伴隨著尾跡向下游運輸直至尾跡周期末期可以觀察到出口處通道渦尺度及總壓損失明顯削減。此時尾跡的頭部正在通過葉柵通道的出口，在t/T=0.9時刻可以觀察到通道渦的尺度明顯小于定常工況，且在任一時刻內葉柵通道內部尾跡頭部附近的通道渦尺度相較于其他位置和定常工況都有所減小，如t/T=0.7時刻尾跡運動到x/Cx=0.9截面附近，此處的通道渦尺度明顯比其他時刻的x/Cx=0.9截面處的通道渦的尺度要小。這說明尾跡對馬蹄渦吸壓力面分支的切斷和削弱作用造成的影響向后傳遞的速度和尾跡向下游出口的運輸速度相當。這也從側面說明了尾跡在葉柵進口處產生的作用會對出口處通道渦的尺度造成較大的影響。

3 結論

為減少端區流動損失大小，對高負荷低壓渦輪尾跡與端區流動機理進行了研究，結果表明尾跡的存在可削弱通道渦的強度從而達到減少端區損失的目的，得出如下結論。

(1)尾跡由于負射流效應對速度進行了一定的削減，但對附面層的厚度未產生較大影響，通過改變附面層厚度去對端區二次流強度產生的影響程度較小。

(2) 尾跡對端區流動結構強度的削減作用主要體現在尾跡對馬蹄渦的吸壓力面分支的切斷破碎作用，破碎后的馬蹄渦向下游運輸后最終會影響葉柵出口處通道渦強度及總壓損失大小。

(3) 尾跡對馬蹄渦吸壓力面分支的切斷和削弱作用造成的影響向后傳遞的速度和尾跡向下游葉柵出口的運輸速度相當，當尾跡的頭部經過葉柵通道的出口時，對端區二次流強度產生了一個削弱作用，有效降低了端區二次流損失，減少了通道渦強度，對減少渦輪流動損失具有重要意義。