序列Kriging仿真優化方法綜述

師路歡，李耀輝，吳義忠，王書亭

（1.許昌學院電氣（機電）工程學院，河南 許昌 461000）

（2.華中科技大學國家企業信息化CAD應用支撐軟件工程技術研究中心，湖北 武漢 430074）

1 引言

隨著設計層次的提升，最優性能備受。因知識缺乏及設計誤差，產品性能將出現偏移甚至導致失效。盡管計算能力持續增強，諸如Ansys等軟件對復雜產品的仿真仍非常耗時。因此，利用Kriging 近似復雜仿真的優化方法成為產品設計領域的熱點[1-2]。主要利用試驗設計、Kriging及潛在估計信息實現仿真的近似、空間探索及優化，具有縮短設計周期、降低研發成本、提升設計精度等特點，適合解決昂貴估值的計算機仿真問題，并廣泛應用于航空航天、機械工程等諸多領域。鑒于此，對序列Kriging的仿真優化方法進行綜述。

2 試驗設計及Kriging模型

2.1 試驗設計

試驗設計（DoE：Design of Experiments）[3]通常以較少試驗次數、較短周期和較低成本來獲得理想結果。全因子設計將試驗各因素在不同水平下進行組合產生采樣點，建模精度較高，但非常耗時，僅用于因素數與水平數較少場合。又出現基于效應稀疏原理和投影特性的部分因子設計、中心復合試驗設計和Box-Behnken試驗設計。但所獲取的設計點缺乏獨立性、隨機性和均勻性。為此，基于全空間填充、非重疊采樣的拉丁超立方設計（LHD）[4]得到廣泛應用。與此相近的正交試驗設計可根據正交性從全因子試驗設計中挑出均勻分散、齊整可比的采樣點，是一種高效率經濟的DoE方法。

2.2 Kriging模型

對于m個設計點X=[x1，...，xm]T，X∈?m×n和目標響應Y=[y1，...，ym]T，Y∈?m×1，經典Kriging[5]的數學表達為：

式中：μ(x)—趨勢函數；z(x)—數據觀測及相關性量化后建立的隨機過程，其均值及方差分別為0和σ2。

當μ(x)等于0、μ和時，分別稱為簡單Kriging、普通Kriging和標準Kriging模型。任意采樣點x與w之間的相關性用協方差E[Z(x)Z(w)]=σ2R(θ，ω，x)表示，通過優化相關參數θ，能夠自適應調整設計點之間的相關性。空間相關函數控制著Kriging 的平滑度、樣本間的相互關系及量化觀測值間的相關性。

對任意x∈?n，(x)被看作能夠找到最佳線性無偏估計λT(x)Y的一個隨機函數，這相當于最小化均方誤差MSE[(x)]=E[λT(x)Y-y(x)]。受無偏估計的約束限制，還需滿足E[λT(x)Yy(x)]=0。且任意點的Kriging表達如式（2）所示。

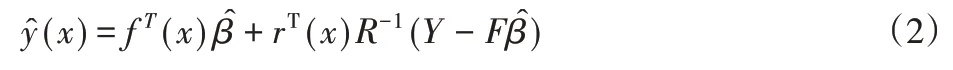
式中：r(x)={R(x，x1)，···，R(x，xn)}T；向量矩陣F由回歸函數f(x)組成；半正定對稱矩陣R由所有已知點之間的自相關性和互相關性組成的最小二乘估計和高斯隨機過程方差的估計可由式（3）和（4）計算獲得。

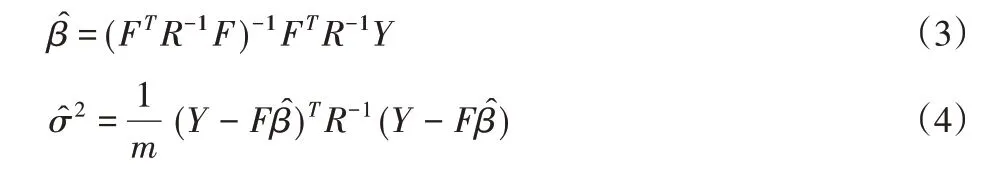
經典Kriging對趨勢函數選擇、模型精度提高及隨機噪聲等問題存在不足。為此對Blind、隨機、Co-Kriging進行綜述。

2.2.1 Blind Kriging 模型

Kriging模型難以預測計算機仿真的全部行為并選擇合適的回歸函數。Blind Kriging 就是利用貝葉斯特征選擇方法拓展了經典Kriging。Blind Kriging［6］通過捕獲樣本數據中最大方差來確定基函數。為此，需考慮一系列候選回歸函數。理想情況下，樣本數據完全通過所選回歸函數來表示，而Kriging中的隨機部分對上述過程僅有較小影響或幾乎沒有影響。

構造Blind Kriging經三個階段：（1）構造初始Kriging，并對相關參數進行最大似然估計；（2）依據估計系數，利用更好的回歸特征函數擴展初始Kriging的回歸函數，同時產生一系列Kriging；（3）最后，根據交叉驗證所估計的誤差決定有效的Kriging是否停止構造或改善。當誤差滿足要求，選擇當前最佳回歸特征函數集構造最終Blind Kriging。

2.2.2 Co-Kriging模型

為探索精確與粗糙模型數據的相關性來，以提高模型的預測精度。Co-Kriging[7]通過已知樣本集和Xe=，分別根據經典Kriging 模型建立低保真度模型yc=和高保真度模型。

建模思路如下：首先利用粗糙數據(Xc，yc)創建經典Kriging模型Yc(x)，然后通過精確數據和粗糙數據間的殘差(Xe，yd)構造第二個Kriging模型，其中yd=ye-ρμc(Xe)，橋接參數ρ是第二個Kriging模型中最大似然估計的一部分。兩個Kriging模型回歸函數和相關函數的選擇等設置依據粗糙數據和殘差分別進行各自調整。

2.2.3 隨機Kriging模型

當出現隨機仿真或存在噪聲情況下，前述Kriging將無法得到正確結果。因此，隨機Kriging 更接近標準的高斯回歸過程。通過獨立的高斯過程ζ(x)建立均值為0、協方差矩陣為Λ的噪聲模型，即ζ～N(0，Λ)建立隨機Kriging。與通用Kriging模型相比，表達式所增加的類似于信噪比矩陣。

2.2.4 三種新Kriging模型的優缺點

為說明三種新Kriging的優缺點，首先，利用Brain作為測試函數，基于相同的初始LHD、最大方差采樣和最終采樣點數，對標準Kriging、Blind Kriging和隨機Kriging模型進行測試比較。其函數圖、梯度圖和方差梯度圖，如圖1所示。

圖1 標準Kriging、Blind Kriging和隨機Kriging的近似結果Fig.1 Approximate Results of Standard，Blind，and Random Kriging

從圖1可看出，Blind Kriging的近似精度最高，但搜索合適的回歸函數需要耗費較長時間。標準Kriging 的精度稍差，但與Blind Kriging相比，精度差別并不明顯，因此，Blind Kriging適合更高精度要求的場合。而加入噪聲的隨機Kriging的近似效果與噪聲均值和方差有必然聯系，適用具有一定分布規律的噪聲函數。然而，隨機Kriging可能存在重復仿真，這使設計者在面對實際復雜的黑箱仿真時無法接受，而重復仿真的解決有待于設計者進一步探索和研究。對Co-Kriging，高低保真度函數的使用無法用二維函數表示。因此，選用一維函數，其近似結果，如圖2所示。

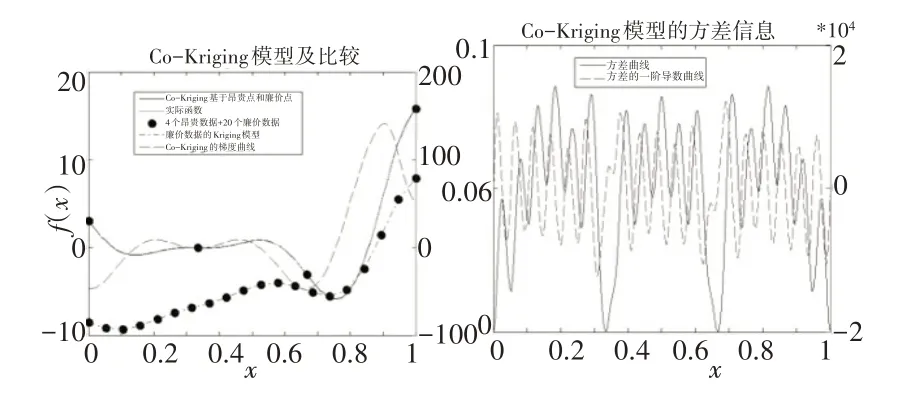
圖2 Co-Kriging模型的測試結果Fig.2 Test Results of the Co-Kriging Model

Co-Kriging的擬合精度更好，但需要具有“廉價”估值并建立兩個Kriging，也需要更大的計算成本。但在高精度仿真模型的近似中，Co-Kriging在近似效果、收斂精度以及實際應用性方面通常好于Blind Kriging。

3 序列Kriging的仿真優化方法

3.1 算法基本框架

依據更新次數，序列Kriging的仿真優化分為一次DoE和序列Kriging優化。較早的一次DoE優化方法以全局近似后的Kriging作為優化目標，利用全局優化方法直接獲取近似最優解。實際上，為保證Kriging更接近實際仿真模型，需要對DoE過程進行優化，使最終DoE數據能夠更均勻、正交的分布到整個設計空間。但可能存在仿真估值次數過多、所構造Kriging無法正常使用、部分采樣點信息量過小以及優化收斂速度過慢或過早收斂等缺點。

多數研究者使用序列Kriging優化方法[9]。仿真估值次數嚴格受限于時間成本，導致優化方法僅在Kriging最優點附近進行更新和細化。因此，該方法利用已知數據信息和Kriging自身參數特征來有效地指導迭代優化搜索朝向具有更大潛在信息量的采樣點，以減少仿真估值次數并快速收斂到全局最優解。設計者如何通過加點采樣準則減少昂貴估值次數以及如何跳出局部最優區域一直是序列Kriging優化的研究熱點。序列Kriging仿真優化的基本框架，如圖3所示。

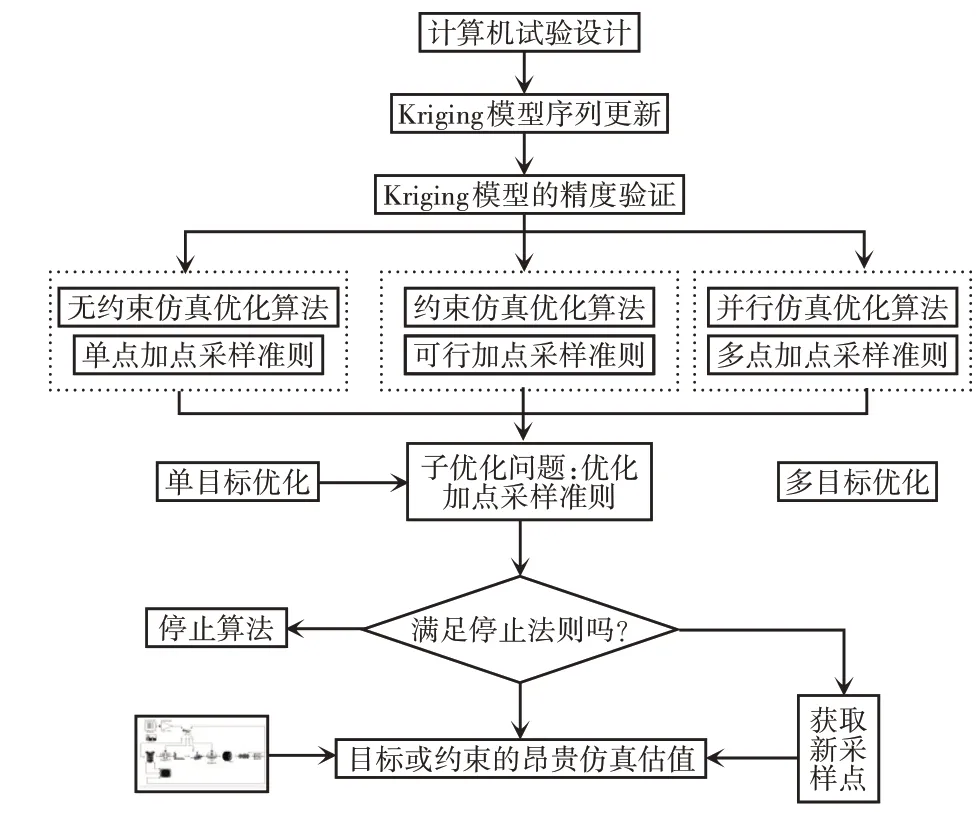
圖3 序列Kriging仿真優化方法的基本框架Fig.3 The Basic Framework of Sequence Kriging Simulation Optimization

Step 1：初始DoE及Kriging建模。利用DoE中的設計方法獲取初始樣本點，在對這些樣本點仿真之后，建立初始的Kriging。

Step 2：模型驗證。在未知設計點處，利用方差等信息對Kriging模型進行精度驗證，并作為算法是否停止的一種判別準則。

Step 3：子優化問題。根據不同優化問題，通過Kriging相關信息建立加點采樣準則，并利用單/多目標全局優化算法對該準則進行優化采樣，獲取新的迭代點。

Step 4：停止準則。根據子優化問題條件，判斷收斂精度或最大仿真次數是否滿足要求，滿足時停止算法，否則，繼續。

Step 5：更新Kriging 模型。對新獲取的采樣點進行仿真估值，并加入到數據樣本集中，利用新的數據點重新構造Kriging模型，并為下一次的子優化做好準備。

結合圖3，對序列Kriging的無約束優化、約束優化及多點并行仿真優化的進展及最新算法分別進行闡述。

3.2 序列Kriging仿真優化方法

3.2.1 序列Kriging的無約束優化方法

最早序列Kriging 優化是在每次迭代過程中產生一個采樣點。目標均值采樣準則通過最小化Kriging 目標來獲取更優化點。然而，真實模型與Kriging之間的最優值存在差異，過多強調目標估計而忽視不確定性因素可能導致局部最優。因此，出現通過最大化Kriging 估計方差來進行序列優化采樣[10]。然而，完全強調全局搜索與優化Kriging目標一樣糟糕。上述兩種思路在提高優化效率和收斂精度方面能力有限。為此，文獻[11]提出了工程應用較為廣泛的無約束EGO方法。結合Kriging預測目標的最小化及采樣位置的不確定性構造出期望改善EI（Expected Improvement）作為加點采樣準則，找到一個具有較大不確定性且較小函數值的設計點。然而，EI或Kriging模型的多峰性與復雜性將增加優化成本，初始樣本的欺騙性會產生較小的標準差估計，這可能導致僅最優解附近的數據點才具有較大EI值，在進行更全局的搜索之前，初始最優解的附近區域將不得不進行更為細致的搜索。

最近，REGIS開發了一種命名為TRIKE（的無約束全局優化方法[12]，并應用于在陡峭又狹窄的全局最小盆域及高維度優化問題中。為每次迭代中，該方法在可信區間內使用信任域策略去最大化EI函數來獲取下一個迭代點，并根據EI實際改善的比率進行信任域區間大小的調整。在一些情況下，使用新的初始填充設計重新開始序列Kriging 的優化算法要勝于繼續尋找全局最優點。在計算昂貴的數據集中，使用新填充設計的重啟策略似乎不符常理。但是，文獻[13]所作的數值測試強有力證明：當算法處于停滯狀態，重啟策略能夠更好地讓算法繼續進行下去，特別是陡峭而狹窄的全局最小盆域。這種方法看似有悖常理，但其成功部分源于以下事實：序列Kriging的優化方法對初始空間填充設計的使用相當敏感。對給定的測試問題，在一種空間填充設計中利用序列Kriging的優化方法可以快速找到全局最小解，利用同樣方法在另一個空間填充設計中將可能花費相當長的時間。當算法在迭代過程中不再有所改善時，通過重啟策略，全局最小值的平均函數估值次數將大幅減小。

盡管EGO的全局收斂性已經確立[14]，但測試結果顯示：EGO在某些常用測試問題中具有較慢的收斂性。但在概率意義上，重啟策略的成功應用可解釋為：在一定假設下，算法找到全局極小或接近最優解的運行次數符合幾何概率分布。對給定確定的初始空間填充設計，TRIKE算法也是確定的。然而，如果使用一個隨機變化的初始空間，那么TRIKE 的行為就像一個隨機算法。因此，重啟策略使優化方法再次收斂到全局最小值成為可能。此外，文獻[15]結合Kriging和遺傳算法提出一種具有穩健搜索能力和良好近似性能的優化算法；文獻[16]利用混合模型（Kriging 和RBF）提出了一種自適應序列全局優化方法。還有結合對偶原理、Kriging模型和信任域策略形成的基于Kriging和對偶變化的全局優化方法[17]。

3.2.2 序列Kriging的并行仿真優化方法

像EGO 和TRIKE 這樣的優化算法在一次迭代過程中只能增加一個新采樣點，對于復雜的仿真優化問題，這需要花費幾周或者更長時間來完成全局尋優。為提高優化效率和收斂速度，可通過在一次循環中獲取多個采樣點并進行并行仿真的序列Kriging并行仿真優化方法實現。

由Jones提出的EGO并行方法通過使用超出不同給定目標的改善概率來選擇不同采樣點[18]，但其性能的優劣與設定目標的閥值水平相關。后來，Chaudhuri等人[19]提出一種自適應的目標設置方法在每次EGO的迭代循環中靈活運用PI加點準則來獲取多個采樣點。文獻[20]使用多目標的加點采樣準則來有效提高改進EGO方法的自身尋優能力。文獻[21]將Kriging的有效全局算法運行到多個代理中，其中一個循環周期內的采樣點數目由代理模型的數量決定。

Ginsbourger教授結合混合蒙特卡羅采樣和分析邊界策略提出的一種并行期望的異步優化方法[22]；基于不確定性逐步減小策略，還提出了幾個新的多點加點采樣準則[23]，特別適合計算成本昂貴的并行仿真優化。最具有代表性的并行仿真優化思想是其所提出的相信趨勢函數的KB（Kriging Believer）策略和利用參數進行持續欺騙的CL（Constant Liar）策略[24]，它們都可通過最大化q-EI加點準則獲取q個采樣點。

KB利用Kriging對采樣點的預測均值替代每次迭代后所選擇采樣點的響應值，以更新Kriging，進而獲取更多新采樣點。多點問題(x′n+1，..，x′n+q)=argmaxX′∈DqEI(X′)的第一種近似求解方法：（1）建立KB(X，Y，q)函數；（2）i=1，i從1到q，做q次循環：①，方差取該點的預測方差；③X=X ?{xn+i}，Y=Y ?{μ(xn+i)}；④循環結束。（3）函數結束。在d維優化上依賴已知EI的貫序策略利用可接受的計算成本提供q個設計點存在失敗風險，因為信任普通Kriging的估計值可能使觀測數據過沖，從而導致陷入非最優區域。為此，又出現降低這種風險的CL策略。

利用給定值L（稱為“謊言”）在每次迭代時更新元模型的CL策略在每次迭代具有相同值L，即：最大化EI找到xn+1好像一直滿足y(xn+1)=L，L∈R。實現步驟如下：（1）建立函數CL(X,Y,q)；（2）i=1，i從1 到q，共做q次循環：①xn+i=argmaxx∈DEI(x)；②X=X?{xn+i}，Y=Y?{L}；③循環結束。（3）函數結束。該策略的關鍵是不同L對最終優化性能的影響。從min{Y}，mean{Y}和max{Y}選一，也可根據權重大小自適應獲取L。

針對Kriging并行仿真優化的其他思路，文獻[25]利用多個初始點優化方法搜索Kriging模型的局部最優解，并圍繞局部最優解的附近區域作進一步搜索，以實現多點采樣；文獻[26]通過最小化目標和最大化EI獲得兩個設計點完成并行采樣；文獻[27]提出了多點加點序列優化采樣方法；文獻[28]人對序列Kriging 的并行全局優化進行了綜述。

盡管上述方法在迭代優化過程中能獲取多個采樣點，但捕獲采樣點所具備的有效信息量不高，也沒有對這些采樣點作進一步的篩選，因此，序列Kriging的并行仿真優化方法仍具有潛在的研究價值。

3.2.3 序列Kriging的約束優化方法

在約束條件已知情況下的序列Kriging優化容易實現。當約束是黑箱時，需要對約束函數進行Kriging 的近似來完成尋優。因此，兼顧約束邊界、點的可行性等因素的約束優化方法值得研究者深入研究。

針對序列Kriging的約束優化，文獻[29]通過EGO方法引入七種加點采樣準則，并對這些準則如何影響全局或局部搜索行為進行詳細的闡述；文獻[30]利用Kriging 所提供目標和約束函數的全局估計以及廣義的EI加點采樣準則提出一種約束優化方法，達到減少目標及約束函數昂貴估值次數的目的。文獻[31]通過新加點采樣準則在可行域內找到Pareto最優解進行昂貴黑箱約束問題的處理；梯度優化方面，文獻[32]依據EGO和基于梯度的優化方法，通過對初始點變異方法、多元插值與非插值響應面函數的研究以及Kriging模型參數的估計，提出了一種基于廣義灰箱約束模型的全局優化方法。針對限制全局優化求解的可行性因素，文獻[33]通過自適應抽樣搜索并確定多個可行性區間，然后在每個可行區間進行局部尋優。文獻[34]闡述了目前常用的幾種優化加點準則及其相應子優化問題的求解與約束處理。

上述約束優化方法只對約束問題的處理提供了一種思路或者只能處理某些簡單的仿真優化問題。且對初始樣本中是否存在可行采樣點以及對其進行判斷和搜索等問題都沒有作具體的考慮和設計。在目標和約束都為黑箱情況下，無法找到合適的加點采樣準則來平衡全局與局部搜索行為。鑒于此，文獻[35]初步實現一種序列Kriging的約束全局優化方法，能夠在初始DoE不存在可行點的情況下完成尋優。此外，Kriging與其他元模型進行混合的全局優化算法也有所發展，比如自適應混合元模型全局優化算法[36]采用外點罰函數方法來處理約束優化問題。

（1）單點采樣的約束優化[37]

通常，黑箱函數f(x)的約束全局優化由式（5）表達。

其中，約束向量g(·)中每個約束將由Kriging近似。加點采樣準則的子優化問題必須考慮約束。整合約束信息主要有兩種策略：第一種是評估約束可行性的概率[38]，第二種是在加點采樣準則的子優化中直接使用約束Kriging的均值。

a）可行性概率方法

假定Kriging 對第i個約束的預測均值和方差用(x)和(x)表示，則該約束的可行性概率可由式（6）表示。

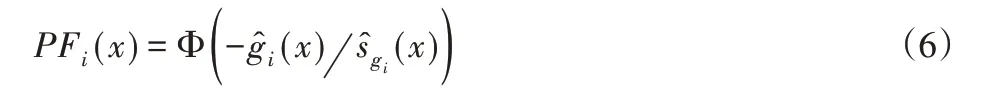
通過EI乘以任意點的可行概率，可將EGO中EI的約束優化問題轉化為一個無約束優化問題。為此，對m個約束的優化問題，其加點采樣準則的表達如式（7）所示。

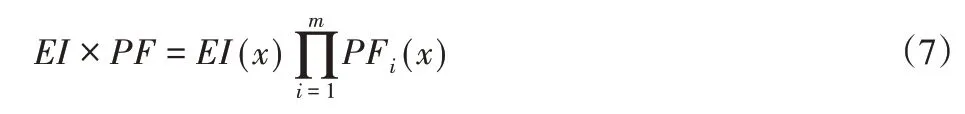
在任何約束條件的可行性非常低的情況下，將迫使EI的大小變為零。因此，可行性概率對EI值的影響比較強烈，并且使得算法無法探索接近約束邊界的點。

b）約束EI法（即直接使用約束Kriging均值的方法）

這種處理約束的方法如式（8）所示。僅僅將EI優化作為一個約束優化問題來解決。由于Kriging均值直接作為約束條件，因此高度依賴于約束Kriging模型的精度。如果約束處于起作用狀態，則會添加接近(x)=0的采樣點。

注意，當出現不連續可行區域且沒有找到可行點，文獻[39]建議使用可行性概率來獲得一個可行初始點。

c）期望違背（EV-Expected violation）

文獻[40]利用期望違背EV代替Kriging約束均值提出一種自適應約束優化方法。其中EV的定義如式（9）所示。

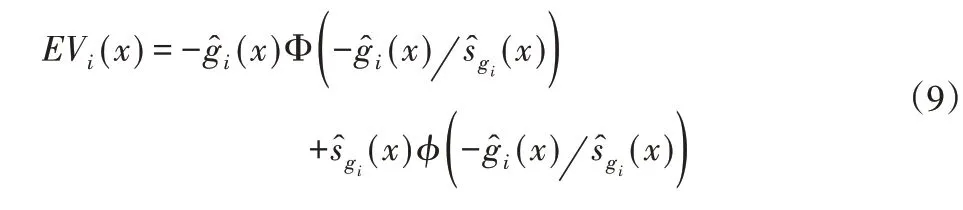
EV 類似于EI準則，約束也要使用Kriging 模型。在沒有約束違背的區域有較高的EV值，即該區域具有較高的不確定性。如果EV高于給定閾值，則可認為該采樣點是可行的。那么，新的EI優化問題定義為：

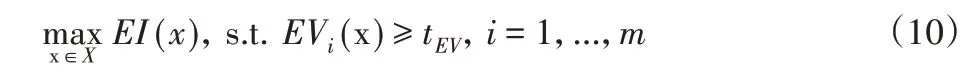
上述三種優化方法效果相當，約束EI法效果略好。

（2）多點采樣之雙目標約束優化

上述的單點采樣方法難以在求解可行性和約束條件之間取得平衡。雙目標約束優化不再將約束問題轉化為無約束優化問題，是將EI和PF作為獨立目標進行優化。如式（11）。

通過考慮獲得目標函數的最小值和滿足約束條件獲取一組Pareto集。所構建Pareto集可讓用戶從多目標優化后的大量采樣點中篩選出更合適的采樣點。而在EGO算法中，只能選擇滿足兩個目標之間可以接受的一個采樣點。需要著重強調的是，使用式（5）的單目標方法確定的單個采樣點與Pareto前沿找到的點并不對應。單目標優化函數是嚴重多峰的，因此將問題視為多目標可以得到更好的采樣點。式（11）的表達可限制PF所允許區域，因優化過程可忽略不起作用約束。然而，在優化之前并不清楚是否為起作用約束，這也限制其適用性。可行性概率的標準形式表明：Kriging 所的估計約束限制區域將小于實際約束限制區域。如果所有不起作用約束都被忽略，那么剩下的約束可以看作等式約束，并且遠離約束邊界的模型精度并不需要給予太多關注。

（3）基于EI、PF和約束預測方差的三目標約束優化方法

在單目標和雙目標優化方法中，沒有考慮約束Kriging模型的預測方差。如果某些區域的方差較大且存在全局最小值，則可能會阻止優化過程在足夠的置信度下找到最優值。在起作用約束下，減少預測方差可能會產生更接近實際約束邊界的最小值。因此，除雙優化目標之外，還可使用第三個目標，即最小化約束Kriging模型的預測方差。約束Kriging的預測方差可以直接用作第三個優化目標，如式（12）所示。另一種方法是使用EV 準則（式9）中的第二部分，如式（13）所示。

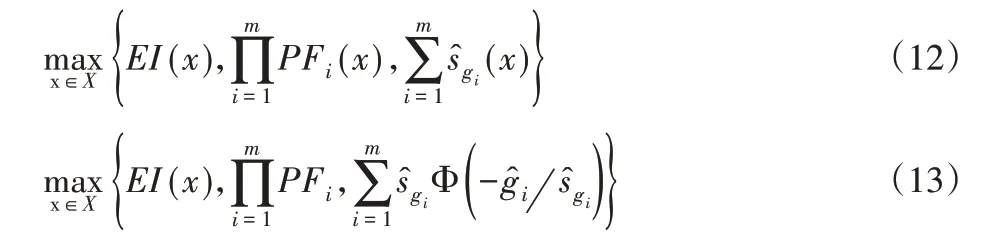
由于僅增加Kriging的預測方差作為第三個優化目標，從Pareto集選擇的點仍然隸屬于雙目標Pareto集中的一部分。

3.2.4 三類優化方法的優缺點

對于無約束的TRIKE算法，利用對稱LHD選擇2（n+1）個初始設計點，并通過基準測試函數Branin、Goldstein Price、Hartman3、Hartman6 與EGO 在相對誤差小于1%條件下進行平均估值次數及標準的比較，以展示TRIKE特點，如表1示。

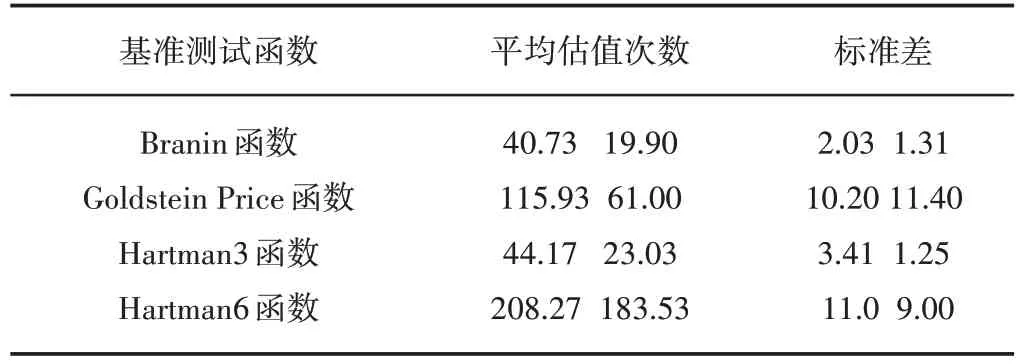
表1 TRIKE（左）和EGO（右）的比較結果Tab.1 Comparison Results of TRIKE and EGO

與EGO相比，TRIKE在局部優化策略上產生了本質性的改善。特別對于高維問題，TRIKE更優于EGO。因此，調整搜索區間的自適應信任域策略更適用序列Kriging的無約束優化，且對陡峭而狹窄的全局最小盆域和高維的Kriging優化問題具有更好的適用前景。然而，對具有幾個局部最優解且平坦的Goldstein Price函數具有略差的優化效果。

以Branin-Hoo 為基準測試函數，以3×3全因子DoE 作為初始采樣，讓四種策略（包括CL 的三種變化策略L=min（Y）、L=max（Y）和L=mean（Y）及KB 策略）在每次循環中增加四個采樣點，比對PI和EI進行比較結果，如圖4所示。

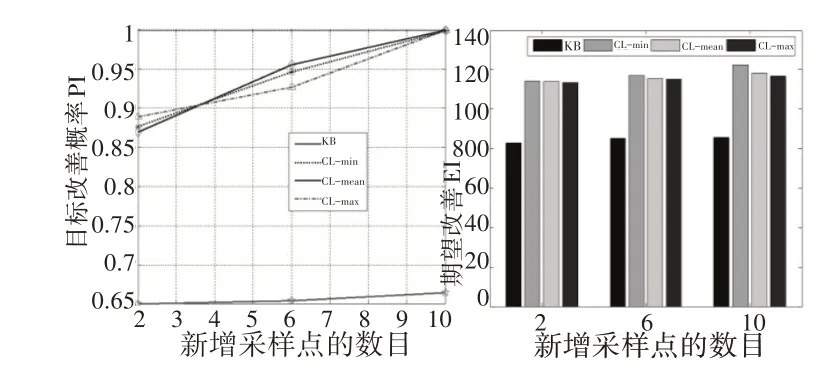
圖4 KB和CL在采樣過程中PI（左圖）與EI（右圖）的比較結果Fig.4 Comparison of PI（left）and EI（right）in KB and CL during Sampling

結果顯示，四種策略都為優化問題提供了空間填充、探索性設計和概率改善。CL[min（Y）]在所考慮的策略中給出了最好的實際改善。新增10個采樣點后，它訪問了測試函數的三個局部最優區域。隨著采樣點的增加，PI和EI也逐漸增大，且CL策略對已經訪問的采樣點會產生排斥。此外，還可以看出，在q-EI標準中，當q增加時，EI的值變化比較小。這較好說明q-EI準則是一種拒絕不恰當采樣點的策略。

存在缺點是：當q增加時，三個CL策略的PI迅速收斂并接近1，從而無法區分采樣點的好壞。根據1改善程度，q-EI更適合進行采樣點的選擇。此外，由于幾乎所有采樣點都被困于初始最優點附近，KB策略的測試結果不盡如人意。

對于約束優化問題，LHD 選擇10個初始采樣點，設置最大函數估值次數為35，然后對單采樣點及基于多目標的多采樣點優化方法進行測試，主要對搜索到的最優解離真實函數最優點的距離、近似約束函數的精度以及最優值附近的均方根誤差進行對比，以說明其優缺點結果，如表2所示。

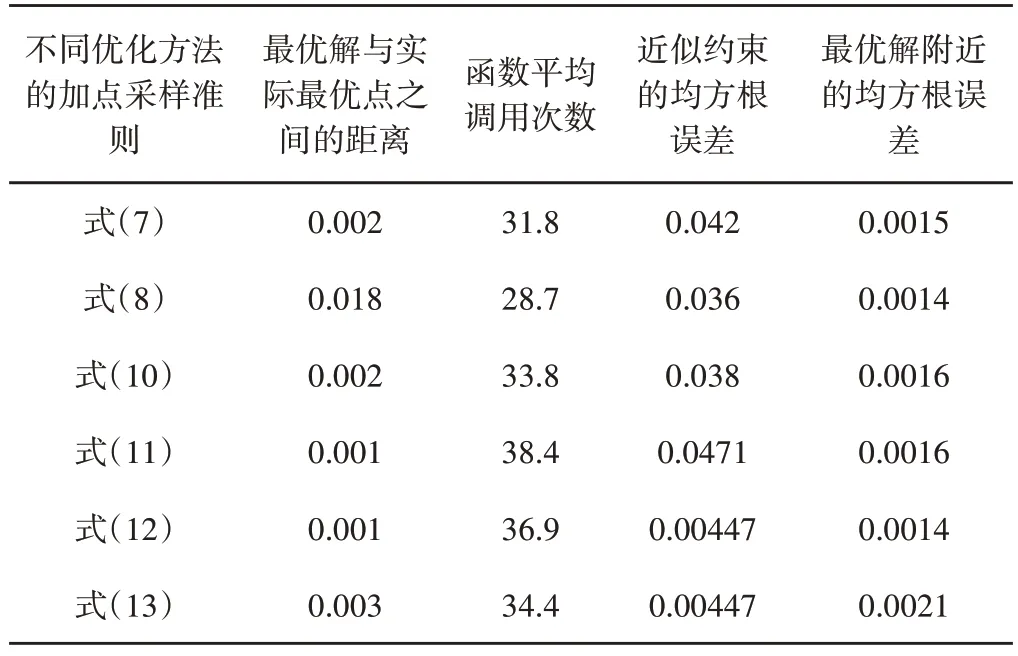
表2 針對優化問題（5）七種優化方法的比較結果Tab.2 Comparison Results of Seven Methods for Problem（5）

這些約束優化方法中，雙目標EI和PF法給出較好結果。三目標準則提供與雙目標方法等價的最優估計，但約束預測的準確性更好。第二個三目標準則在整個空間得到最好的約束精度，但其對約束搜索給予太多關注，導致略差的最優值估計。此外，最優解附近的均方根誤差表明，單目標優化方法主要聚集在最優解附近進行更優點的搜索，在均衡全局與局部搜索行為方面，多目標優化顯示了更大的優越性。總之，單目標優化具有較少的函數調用次數，而多目標具有較好的優化結果。對于將約束Kriging的預測方差直接用作第三個優化目標的約束優化方法，這三個優化目標的關系，如圖5所示。

從圖5可看出：在約束Kriging的預測均方差的影響下，三個目標的Pareto 前沿數據相當于從原雙目標Pareto 前沿中刪除了一些采樣點。輸入方面，在約束Kriging預測準確性較高的情況下，來自Pareto前沿的點將更加分散，這有助于減少約束邊界的不確定性。總之，多個目標優化選擇多個采樣點的優化法方法明顯優于單個目標獲取一個采樣點的優化方法。

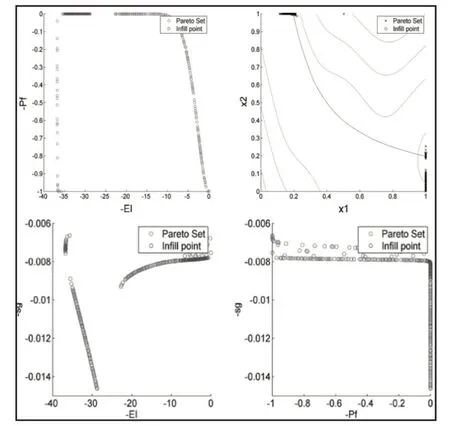
圖5 利用Kriging預測均方差作為第三個目標的優化方法的測試結果Fig.5 Result on Optimization Using Predicted MSE as Third Objective

3.3 算法終止條件

序列Kriging仿真優化的終止條件考慮以下三方面：（1）Kriging的精度是否滿足給定精度要求；（2）是否達到最大昂貴仿真次數；（3）一些參數值（比如均方根誤差等）是否小于給定容差。通常使用交叉驗證法（CV-Cross Validation）[41]和均方根誤差（RMSE）估計法[42]對Kriging模型進行評價。

由于序列Kriging仿真優化的目的是在較少昂貴估值下獲取全局近似最優解，因此，最大昂貴仿真次數是常用的優化停止條件，昂貴仿真次數的多少通常與優化問題或實際實驗的維度和復雜度相關。如果超出，利用Kriging近似模型進行仿真優化將毫無意義。此外，設計者更熱衷于使用優化過程中的某些參數是否小于給定容差作為停止條件，比如期望改善EI小于0.001、兩次獲得的最優解相差甚小等等。然而，對于實際測試問題，設計者通常會將上述終止準則中的兩個或多個結合起來使用，當任何一個條件滿足時，就停止優化。

4 軟件工具箱

Kriging在近似計算密集的仿真模型中備受歡迎。為了給設計者提供方便，序列Kriging仿真優化方法的工具箱包括：

（1）DACE 工具箱。DACE 是Matlab 工具箱，用于計算機仿真模型的Kriging近似。該軟件包括DoE方法。軟件下載請訪問http：//www2.imm.dtu.dk/projects/dace/。

（2）DiceKriging 及DiceOptim 工具。DiceKriging 和DiceOptim是兩個R語言軟件包，用于近似和優化昂貴估值的確定性目標函數。DiceKriging 工具箱對各種Kriging 模型進行模擬、預測和驗證。DiceOptim 能夠基于EI的單點和多點采樣準則完成序列Kriging 的全局優化。軟件包下載請訪問https：//cran.r-project.org/web/packages/DiceKriging/index.html和https：//cran.r-project.org/web/packages/DiceOptim/index.html。

（3）ooDACE工具箱。基于Matlab的ooDACE工具箱提供了強大、靈活且易于擴展的框架。不同類型的Kriging在同一平臺下通過面向對象的方式實現。可以完成Co-Kriging、隨機Kriging、Blind Kriging、梯度增強Kriging 和通用Kriging 的近似建模，高效的超參數仿真優化。還可以利用交叉驗證、積分的均方差等精度預測方法對模型進行評估。軟件包下載請訪問http：//sumo.intec.ugent.be/ooDACE_download。

（4）SuperEGO工具箱。SuperEGO也是基于Matlab語言，將智能采樣策略、Kriging建模方法、諸如Direct算法的全局優化方法以及優化終止條件整合在一起完成通用Kriging的全局近似及仿真優化。該軟件包并不公開，如果僅用于個人或教育用途，可向開發者獲取。

（5）Surrogates optimal toolbox 等。基于Matlab 的Surrogates optimal工具箱主要適用于連續、整數或混合整數變量且計算昂貴的黑箱全局優化問題。對于計算成本低的函數評估，工具箱的優化效果可能不是非常有效。軟件包下載可訪問https：//sites.google.com/site/srgtstoolbox/。

5 總結與展望

序列Kriging的仿真優化方法一般只需要少量昂貴估值就能夠明顯看出函數趨勢且快速得出結論。基于序列搜索的優化過程中，近似的Kriging模型能夠在未采樣點處為優化提供預測目標和方差的估值，這些信息結合有效的全局優化方法能夠在平衡全局與局部搜索行為的基礎上搜索合適的全局近似最優解，有效促進了對模型的直覺理解和開發。

針對序列Kriging仿真優化方法，還面臨許多挑戰：

（1）關于Kriging 模型中相關矩陣R 的病態問題。理論上，Kriging 的相關函數是完全單調的，因此，R 應保證是半正定的。而相關矩陣出現異常可能存在兩種原因。第一，如果函數非常平滑且可預測，那么樣本點將會高度相關，這意味著相關矩陣的每一列幾乎是一個全為1的列，從而導致這些列的極高共線性；第二，優化運行接近尾聲時，算法所增加的點往往接近先前的采樣點。當兩個采樣點非常接近的時候，R中與這些采樣點相應的列將幾乎是一樣的，導致R出現奇異情況。如果僅僅是計算Kriging目標估計及其標準差的話，這種病態是易于管理的，但計算邊界時，將產生較大麻煩。

（2）EGO中期望改善函數的復雜性。EGO方法在一些情況下確實能夠找到較好近似最優解。但因EI函數的復雜性和多峰性可能導致較長的優化時間。此外，初始樣本的欺騙性可能會產生較小的標準差估計，這往往導致算法更多地關注局部探索區域，直到這種不確定性變得很小。結果，僅僅接近當前最優解的數據點有大的EI值。而且，在初始Kriging已經獲得精確最優解的情況下，EGO沒有任何優點。因此，如何選擇有效的加點采樣準則來保證EGO在恰當的時候合理跳出局部最優區域一直是設計者研究的重點和難點。

（3）并行優化采樣具有更大的發展潛力。相對于昂貴仿真估值，優化時間的消耗幾乎可以忽略不計，每次迭代獲得q個設計點的采樣準則將使總優化時間減少為原來的近1/q。目前大多數優化方法在每次迭代中僅產生一個新采樣點，或者所獲取的多個采樣點無法定位到設計空間的不同盆型區域，從而導致搜索到的多個采樣點無法為循環優化提供更多有價值的信息。如何利用深度技術在序列迭代中產生多個更優前景的采樣點，以提高優化效率和收斂精度，有待于進一步研究。

（4）約束為黑箱優化問題處理。目標和約束的黑箱性將導致序列Kriging約束優化方法的優化難度驟然增加，大多文獻只對約束問題的處理提供了一種思路或者只能處理某些特殊問題。且對初始樣本中是否存在可行采樣點以及對其進行判斷和搜索等問題很少作具體的考慮和設計。特別在目標和約束都為昂貴黑箱條件下，無法找到合適的加點采樣準則來平衡全局與局部搜索行為。這為該方向的深入研究留下充足空間。