盤式剎車與齒輪耦合動力學(xué)模型及動力學(xué)行為

韋堯中，向 東，沈銀華

（清華大學(xué)機(jī)械工程系，北京 100084）

1 前言

以驅(qū)動裝置，變速齒輪箱，盤式剎車裝置，負(fù)載為傳動形式的傳動鏈形式廣泛存在于汽車、風(fēng)電裝備中。傳動鏈經(jīng)常會受到盤式剎車裝置緊急剎車的影響，如風(fēng)電傳動鏈會因為風(fēng)機(jī)部件故障和風(fēng)速異常等原因緊急剎車。緊急剎車時會給傳動系統(tǒng)帶來沖擊力和沖擊力矩，給與其固聯(lián)的齒輪副帶來非正常工況，齒輪系統(tǒng)在這種非正常工況下表現(xiàn)出異常振動，甚至出現(xiàn)輪齒非正常嚙合等現(xiàn)象，影響齒輪正常壽命，需要對其進(jìn)行研究。

國內(nèi)外眾多學(xué)者在齒輪嚙合過程、剎車系統(tǒng)剎車過程的動力學(xué)行為進(jìn)行了大量研究。文獻(xiàn)[1]通過沿齒寬方向切片將斜齒輪轉(zhuǎn)換成沿齒寬分布的直齒輪計算斜齒輪時變嚙合剛度。文獻(xiàn)[2-3]在齒輪動力學(xué)行為計算過程中考慮摩擦力影響，表明摩擦力是嚙合過程重要影響因素。文獻(xiàn)[4-5]在計算過程中考慮輪齒齒側(cè)間隙，并證明其在齒輪嚙合過程中的影響。盤式剎車系統(tǒng)研究方面，文獻(xiàn)[6-7]建立盤式剎車裝置剎車盤和摩擦片的動力學(xué)模型，并考慮二者間時變摩擦系數(shù)計算得到剎車過程中的轉(zhuǎn)矩波動等情況。上述研究均在齒輪嚙合、盤式剎車系統(tǒng)剎車過程建立了精確的計算模型，但都是針對各個部件本身進(jìn)行討論，缺乏二者耦合情況下動力學(xué)行為的研究。

建立包含驅(qū)動裝置、齒輪箱、剎車系統(tǒng)、負(fù)載的耦合多體動力學(xué)模型以表征二者耦合情況下系統(tǒng)的動力學(xué)行為。同時為精確表征行為細(xì)節(jié)，對剎車系統(tǒng)和齒輪系統(tǒng)均進(jìn)行詳細(xì)建模。在對剎車系統(tǒng)建模過程中考慮剎車盤摩擦系數(shù)變化，在對齒輪系統(tǒng)建模的過程中，考慮齒輪副嚙合過程的時變嚙合剛度，齒側(cè)間隙和摩擦力等主要因素，并考慮發(fā)生拍擊輪齒兩側(cè)嚙合剛度及力方向的差異。之后以某實驗臺為具體對象進(jìn)行仿真分析并進(jìn)行實驗驗證，對比實驗和仿真剎車過程中振動、轉(zhuǎn)速轉(zhuǎn)矩變化等信息驗證模型的準(zhǔn)確性。

2 傳動鏈多體動力學(xué)模型

包含驅(qū)動端、單級平行軸齒輪箱、剎車系統(tǒng)、負(fù)載的多體動力學(xué)模型，如圖1所示。

圖1中：從左下至右上的傳動部件依次為原動機(jī)、傳動軸、主動齒輪、被動齒輪，傳動軸、剎車裝置和負(fù)載。圖中：y軸方向與正常嚙合嚙合面方向重合。其中主動斜齒輪為大齒輪且為右旋齒輪。動力學(xué)方程表示為：

圖1 多體動力學(xué)模型Fig.1 Dynamic Model

式中：Ji，θi，mi，xi，yi，zi—部件i的轉(zhuǎn)動慣量，轉(zhuǎn)角，質(zhì)量，x軸，y軸和z軸方向的位移，下標(biāo)i=p，g，b1，b2，1，0—對應(yīng)小齒輪，大齒輪，剎車系統(tǒng)摩擦片，剎車系統(tǒng)摩擦盤，負(fù)載端和驅(qū)動端。kij，cij—部件i在j方向上的支撐剛度和阻尼，i的含義與上文相同，j=x，y，z分別對應(yīng)x軸，y軸和z軸方向；Fj—嚙合力在j方向上的分力；T0(t)—驅(qū)動轉(zhuǎn)矩；N(t)—摩擦片制動壓力；μ—剎車系統(tǒng)摩擦系數(shù)；Mpy，Mgy—嚙合力對大小齒輪的彎矩；Mfp，Mfg—兩個齒輪摩擦力矩；fij—齒輪i在j方向上的摩擦力。

模型中的嚙合力和摩擦力隨齒輪嚙合情況變化。其中，嚙合力受到嚙合狀態(tài)、齒輪嚙合剛度的影響，二者均為時變量。摩擦力與接觸點嚙合力、運動狀態(tài)和幾何形貌有關(guān)，也是時變量。下面介紹齒輪嚙合狀態(tài)、時變嚙合剛度影響下嚙合力計算方法，與嚙合力、運動狀態(tài)和幾何形貌相關(guān)的摩擦力計算方法以及剎車盤變摩擦系數(shù)計算方法。

2.1 嚙合力計算

嚙合力大小與圖1中P，G兩點相對位移有關(guān)，由二者幾何位置關(guān)系可得兩點相對齒面法向位移和相對速度為：

式中：=yp+zptan(βb)+θprpb—小齒輪在y方向上的位移；=yg+zgtan(βb)+θgrgb—大齒輪在y方向上的位移；e—嚙合誤差；βb—基圓螺旋角；rpb，rgb—小齒輪和大齒輪基圓半徑。

由于齒輪存在圖2所示齒側(cè)間隙2b，文中b=10-5mm，當(dāng)嚙合點間相對位移大于二分之一側(cè)隙即δ＞b時，主動齒輪正常嚙合齒面參與嚙合，當(dāng)-b＜δ＜b時，為脫齒狀態(tài)，輪齒間不接觸，δ＜-b時為非正常嚙狀態(tài)，主動齒輪齒背參與嚙合。

圖2 齒側(cè)間隙示意圖Fig.2 Backlash of Gear Pair

嚙合力計算采用KELVIN-VOIGT模型，可表示為：

km與齒輪實時嚙合位置有關(guān)。對直齒輪，詳細(xì)計算方法見文獻(xiàn)［8］，計算過程中需計算輪齒彎曲剛度和齒根附加變形剛度，二者計算使用參量分別見圖3（a）和圖3（b），由于計算過程中均用到關(guān)鍵嚙合參數(shù)αm，而，其中αi—該點的壓力角，s，r，αn—分度圓齒厚、半徑和壓力角。故將嚙合點壓力角作為剛度計算重要中間參量。

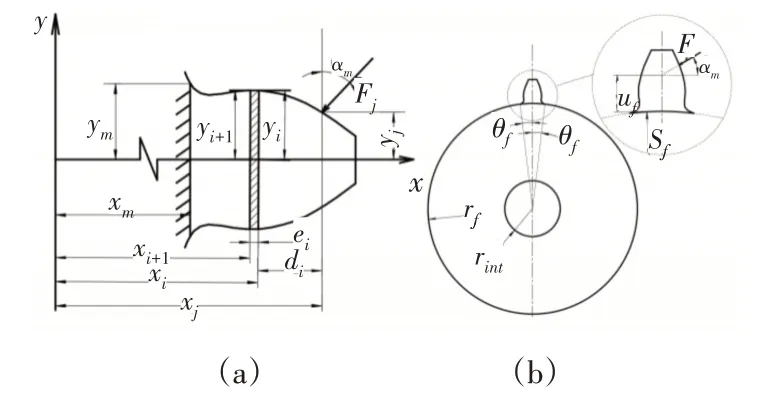
圖3 齒輪彎曲剛度和齒根附加變形剛度計算參數(shù)Fig.3 Parameters of Bending Stiffness and Fillet-Foundation Stiffness

對斜齒輪，嚙合剛度解析算法采用沿齒寬方向切片的方法處理，具體方法見文獻(xiàn)［1］。切片后，各個齒片嚙合剛度按照直齒輪計算，各個齒片嚙合位置以端面為基準(zhǔn)，可根據(jù)嚙合面內(nèi)各個齒片嚙合點與端面嚙合點相對位置求出，并依此求出各個齒片嚙合點的壓力角，將各個齒片看成直齒輪進(jìn)行計算，最后通過各個齒片嚙合剛度加和即可求出km，如式（5）。

式中：n—沿齒寬切片數(shù)目，kbgj，kfgj，kbpj，kfpj—第j片嚙合輪齒的大齒輪輪齒彎曲剛度，齒根附加變形剛度，小齒輪輪齒彎曲剛度，齒根附加變形剛度。kh為接觸剛度，以上參數(shù)計算均按照直齒輪計算方法，在此不做贅述。

由于輪齒發(fā)生拍擊時，同一輪齒位置齒面和齒背對應(yīng)的嚙合剛度不同，需分別計算，如圖4所示。正常嚙合線為N1N2，嚙合點為A點。齒背嚙合時嚙合線為M2M1，嚙合點為B點，前文所述嚙合剛度計算時通常使用嚙合點壓力角，兩個點的壓力角轉(zhuǎn)換關(guān)系為：

圖4 正常及非正常嚙合過程Fig.4 Normal and Abnormal Meshing Process

式中：αA，αB—嚙合點A和嚙合點B的壓力角；sgb—大齒輪基圓齒厚；sN1M1—大齒輪N1M1段弧長。

2.2 齒輪嚙合摩擦力計算

根據(jù)文獻(xiàn)［3］提出的算法，齒輪摩擦系數(shù)為：

式中：μ—齒輪間摩擦系數(shù)；

μBDR—邊界油膜彈流潤滑平均系數(shù)，取0.08。

μEHL—全油膜潤滑平均摩擦系數(shù)。參考文獻(xiàn)［9］，計算式如下：

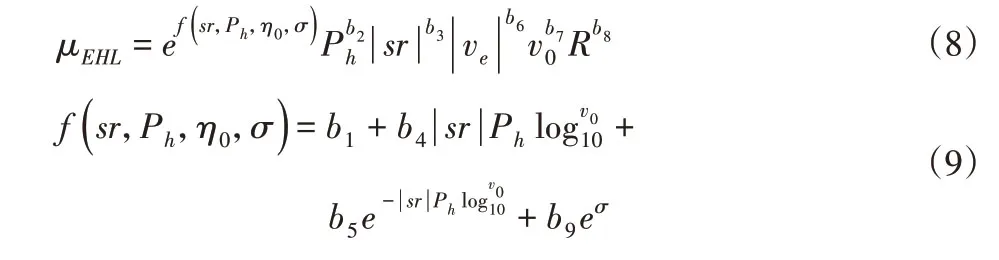
式中：sr—齒輪副滑滾比；

ve—齒輪相對滑動速度；

η0—常溫下潤滑油動力粘度；

σ—齒廓表面粗糙度均方根；

σp和σg—大小齒輪表面粗糙度；

R—嚙合點出處當(dāng)量曲率半徑，其中rg，rp—大小齒輪嚙合處曲率半徑，bk取值，如表1所示。Ph—最大赫茲接觸應(yīng)力，0.5。

其中，F(xiàn)n—表面收到的實際壓力；E—彈性模量；ε—泊松比；L—齒寬；Tmin最小油膜厚度計算如下［10］：

式中：vm—齒面平均速度。

對斜齒輪每一個嚙合點的嚙合力、速度和曲率半徑關(guān)系各不相同，利用前文所述切片方法將齒輪沿齒寬離散，對每個齒片按照直齒輪處理即可求得各個嚙合點的摩擦計算條件。當(dāng)齒輪處于正嚙合狀態(tài)時,；齒背嚙合時，方向根據(jù)齒面切向相對值確定。Mfg，Mfp使用各個嚙合點摩擦力與摩擦力臂乘積計算得到，在此不贅述。

2.3 剎車盤摩擦力計算

剎車盤摩擦系數(shù)計算采用經(jīng)典STRIBECK 模型［11］，剎車盤與摩擦片相對速度為0時為粘滯狀態(tài)，此時摩擦力計算式如下：

式中：fs—最大靜摩擦力；

fe—切向力。

當(dāng)相對速度不為0時，摩擦系數(shù)計算如下：

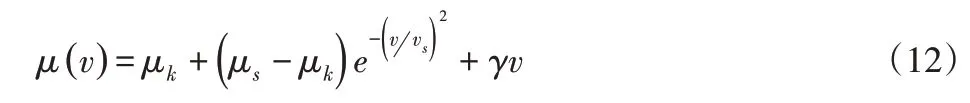
式中：μk—滑動摩擦系數(shù)，取0.25；

μs—最大靜摩擦系數(shù)，取0.4；

v—摩擦塊和剎車盤的相對運動速度；

vs—STRIBECK 速度，文中取10m/s；γ—粘性系數(shù)，文中取0.0009，摩擦力方向由二者相對速度方向確定。

3 求解結(jié)果及驗證

3.1 仿真參數(shù)及載荷

仿真參數(shù)設(shè)定，如表1所示。表1中大小齒輪質(zhì)量和轉(zhuǎn)動慣量均將固聯(lián)的齒輪軸和聯(lián)軸器計算在內(nèi)，參數(shù)符號與前文相同。

表1 仿真參數(shù)Tab.1 Simulation Parameter

驅(qū)動轉(zhuǎn)矩和摩擦片壓力隨時間變化，如圖5所示。其中驅(qū)動轉(zhuǎn)矩T0曲線根據(jù)實際驅(qū)動轉(zhuǎn)矩曲線，如圖6所示。

圖5 仿真載荷曲線Fig.5 Simulation Load Curve

圖6 實驗載荷曲線Fig.6 Experiment Load Curve

由于關(guān)注剎車過程，實際運行時扭矩上升狀態(tài)和扭矩平穩(wěn)狀態(tài)時間壓縮，但保持原有變化趨勢，用9段不同的函數(shù)表示，摩擦片壓力Fn用3段函數(shù)表示。式（1）所示動力學(xué)方程使用NEWMARK法解，時間步長取10-7s，仿真時間1.2s，輪齒沿齒寬方向切片數(shù)為200，當(dāng)轉(zhuǎn)速下降到0時，根據(jù)實驗情況將負(fù)載端抱死。

3.2 仿真結(jié)果及討論

根據(jù)前文所述仿真參數(shù)和仿真條件，計算得到P，G兩點相對位移差δ，從動齒輪轉(zhuǎn)速和y軸方向加速度分別如圖7（a），7（b），7（c）所示。圖7（a）中，δ＞10-5mm時，主動齒輪正常嚙合齒面參與嚙合，當(dāng)-10-5mm ＜δ＜10-5mm 時，輪齒間不接觸，δ＜-10-5mm時為非正常嚙狀態(tài)，主動齒輪齒背參與嚙合。由圖7可以看出，第0.884s時，從動輪轉(zhuǎn)速降到6.6rad/s，同時，齒輪軸向加速度增大，之后齒輪開始出現(xiàn)脫齒，齒面出現(xiàn)碰撞，當(dāng)齒輪轉(zhuǎn)動停止時振動最大。剎車過程使齒輪轉(zhuǎn)速降低，當(dāng)轉(zhuǎn)速低至一定程度時，輪齒出現(xiàn)拍擊，并造成振動幅度增大。

圖7 接觸點相對位移、轉(zhuǎn)速、轉(zhuǎn)矩仿真結(jié)果Fig.7 Simulation Results of Contact Points Relative Displacement，Rotating Speed and Torque

3.3 仿真結(jié)果驗證

針對圖1所示多體動力學(xué)模型搭建動力學(xué)實驗臺，實驗臺結(jié)構(gòu)簡化圖，如圖8所示。實驗臺結(jié)構(gòu)參數(shù)與表1保持一致。實驗臺測量參數(shù)為輸入軸轉(zhuǎn)矩，輸出軸轉(zhuǎn)速，從動輪軸端振動。

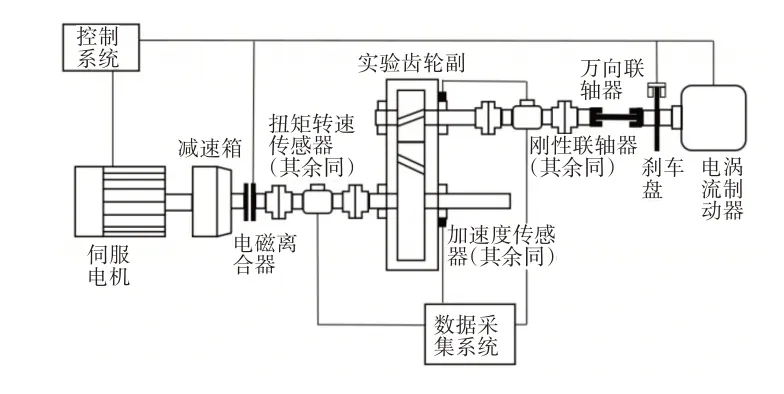
圖8 實驗傳動臺結(jié)構(gòu)圖Fig.8 Experiment Drive Train Structure

實驗臺輸出軸轉(zhuǎn)速，輸出軸軸端振動情況，如圖9所示。圖9中，剎車時間為第4.76s，由于電磁離合器的并未完全消磁，使得電機(jī)依舊能夠提供轉(zhuǎn)矩使得轉(zhuǎn)矩上升。根據(jù)圖9（a）和圖9（b）當(dāng)輸出軸轉(zhuǎn)速下降到170r/min時，從動齒輪軸端振動增大，當(dāng)輸出軸轉(zhuǎn)速為0時，振動達(dá)到最大，之后逐漸衰減，與仿真過程一致。

圖9 轉(zhuǎn)速、轉(zhuǎn)矩實驗結(jié)果Fig.9 Experiment Result of Rotating Speed and Torque

4 結(jié)論

通過建立齒輪、盤式剎車裝置的耦合動力學(xué)模型，通過仿真計算揭示盤式剎車裝置在制動時，齒輪在低速狀態(tài)會產(chǎn)生拍擊現(xiàn)象，并造成軸端振動加劇。之后通過搭建與模型一致的實驗臺，并進(jìn)行剎車實驗，實驗結(jié)果表明，緊急剎車過程中當(dāng)齒輪轉(zhuǎn)速降低到一定程度時，齒輪軸端振動會加劇，齒輪在該狀態(tài)下發(fā)生了非正常嚙合，說明本文所述仿真模型可以分析齒輪和盤式剎車系統(tǒng)耦合動力學(xué)行為。

并通過仿真和實驗說明在剎車工況下，齒輪在低轉(zhuǎn)速時會發(fā)生非正常振動現(xiàn)象，影響齒輪嚙合。研究結(jié)果為今后優(yōu)化剎車策略提供模型支撐。