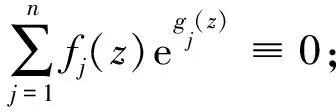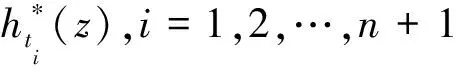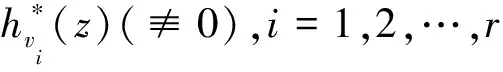一類復q-平移差分-微分多項式的值分布

鄭秀敏，占美龍

(江西師范大學數學與統計學院，江西 南昌 330022)

1 引言與結果

本文中，我們使用Nevanlinna理論的標準記號和基本結果(見文[1-3])。若無特殊說明，亞純函數是指在整個復平面上亞純的函數。我們用記號σ(f)表示f(z)的級，用記號λ(f-c)表示f(z)-c的零點收斂指數，其中c∈∪{∞}。

眾所周知，在亞純函數值分布理論的研究中，微分多項式的值分布研究是一個經典問題。該問題源自W.K.Hayman在文[4]中提出的猜想:當f(z)為超越亞純函數且n∈+時，f(z)nf′(z)取任意非零復數無窮多次。隨后，許多學者致力于對復差分多項式的值分布進行研究，得到了許多有意義的結果。這些結果可視為相應復微分多項式值分布結果的差分模擬。其中，文[5]和文[6]中的結果可以看作是上述W.K.Hayman經典結果的最直接的差分模擬結果。2014年，鄭秀敏和徐洪焱在文[7]中研究了Valiron-Mokhon’ko定理的微分-差分模擬結果，并運用該結果研究了某類微分-差分多項式的虧量。同時，上述結果可進一步推廣至q-差分情形和q-平移差分情形，具體可見以下兩個結果。

2011年，劉凱和祁小光在文[8]中研究了q-平移差分多項式f(z)nf(qz+η)的值分布，得到了以下結果。

定理A[8]設f(z)為零級超越亞純函數，q為非零復常數。則當n≥6時，q-平移差分多項式f(z)nf(qz+η)取任意b∈{0}無窮多次。

2013年，涂金和鄭秀敏在文[9]中將條件“n≥6”減弱到“n≥5”，改進了定理A。

注意到定理A中考慮的是f(z)具有零級的情形。由此，我們自然提出問題:當f(z)具有正有窮級時，結果又會怎樣?對于該問題，徐娜等在文[10]中研究了q-差分-微分多項式[f(z)f(qz)](k)的值分布，其中f(z)為具有正有窮級的超越整函數，得到結果如下。

定理B[10]設f(z)為超越整函數且滿足0<σ(f)<∞，a為f(z)的有窮Borel例外值，q∈{0，1}且使得qσ(f)≠±1。記H(z)=[f(z)f(qz)](k)，則以下結論成立。

(1) 若a=0，則0亦為H(z)的Borel例外值，即H(z)沒有非零有窮Borel例外值。

(2) 若a≠0，則H(z)沒有有窮Borel例外值。

(3)H(z)取任意c∈{0}無窮多次，且滿足λ(H-c)=σ(f)。

受定理A和定理B的啟發，我們考慮形式更一般的q-平移差分-微分多項式的值分布。一方面，我們用q-平移差分f(qz+η)和f(qz+η)-f(z)替代f(qz)。另一方面，我們將f(z)推廣為f(z)的多項式。在敘述所得結果之前，我們先引入以下記號。設

P(z)=anzn+an-1zn-1+…+a1z+a0，n∈+

為非零多項式，其中a0，a1，…，an(≠0)為復常數。又記m∈+為P(z)的不同零點個數，則P(z)可以表示成

P(z)=an(z-α1)n1…(z-αm)nm

其中α1，α2，…，am∈為P(z)的不同零點，n1，n2，…，nm∈+且滿足

首先，我們考慮q-平移差分-微分多項式[P(f)f(qz+η)](k)的值分布，推廣了定理B。

定理1.1設f(z)為超越整函數且滿足0<σ(f)<∞，a為f(z)的有窮Borel例外值，η∈，q∈{0，1}且使得qσ(f)≠-1，-2，…，-n。記

H1(z)=[P(f)f(qz+η)](k)，k∈+

則H1(z)沒有非零有窮Borel例外值，即H1(z)取任意c∈{0}無窮多次，且滿足λ(H1-c)=σ(f)。

其次，我們用f(qz+η)-f(z)替換f(qz+η)，得到相應結果如下。

定理1.2設f(z)為超越整函數且滿足0<σ(f)<∞，a為f(z)的有窮Borel例外值，η∈，q∈{0，1}且使得qσ(f)≠-1，-2，…，-n，f(qz+η)?f(z)。記

H2(z)=[P(f)(f(qz+η)-f(z))](k)，k∈

則以下結論成立。

(1) 若qs=1，m=1且a=α1，則0亦為H2(z)的Borel例外值，即H2(z)沒有非零有窮Borel例外值。

(2) 若qs≠1或qs=1，m≠1，或qs=1，m=1，a≠α1，則H2(z)沒有有窮Borel例外值。

(3)H2(z)取任意c∈{0}無窮多次，且滿足λ(H2-c)=σ(f)。

2 定理1.1和定理1.2的證明

為證明定理1.1和定理1.2，我們需要以下兩個引理。

引理2.1[11]設n∈+，P1(z)，P2(z)，…，Pn(z)是次數分別為d1，d2，…，dn的非常數多項式且滿足當i≠j時，deg(Pi-Pj)=max{di，dj}。令

其中Bj(z)(?0)，j=1，2，…，n為整函數且滿足σ(Bj)

引理2.2[3]設n≥2，f1(z)，f2(z)，…，fn(z)為亞純函數，g1(z)，g2(z)，…，gn(z)為整函數，且滿足下列條件：

(2) 對于1≤j

(3) 對于1≤j≤n，1≤h

下面證明定理1.1和定理1.2。

定理1.1的證明因α1，α2，…，am為P(z)的不同零點，則P(f)可以表示

P(f)=an(f-α1)n1(f-α2)n2…(f-αm)nm

(2.1)

其中an≠0，n1+n2+…+nm=n。因f(z)為有窮正級超越整函數，且a為其有窮Borel例外值，故f(z)可以表示成

f(z)=a+g(z)eαzs

(2.2)

其中α(≠0)為復常數，s(≥1)為整數且滿足σ(f)=s，g(z)(?0)為整函數且滿足σ(g)

f(qz+η)=a+g(qz+η)h(z)eqsαzs

(2.3)

其中h(z)(?0)為整函數且滿足σ(h)≤s-1。因此，由(2.1)～(2.3)式可得

ang(z)ng(qz+η)h(z)e(n+qs)αzs

(2.4)

P(f)f(qz+η)=ang(z)ng(qz+

η)h(z)e(n+qs)αzs

(2.5)

因qs≠-1，-2，…，-n，α≠2α≠…≠nα，qsα≠(1+qs)α≠…≠(n+qs)α，且g(z)h(z)?0，σ(g)

(2.6)

其中βl=

情形1若僅存在一個βl0∈{α，2α，…，nα}∪{qsα，(1+qs)α，…，(n+qs)α}使得

H1(z)=gl0(z)eβl0zs

其中gl0(z)為(2.6)式中項eβl0zs的相應系數之和。顯然，βl0≠0，gl0(z)?0，σ(gl0)

情形2對其它情形，不失一般性，設

H1(z)=gl1(z)eβl1zs+gl2(z)eβl2zs+…+glr(z)eβlrzs

(2.7)

其中r∈{2，…，2n+1}，βl1，βl2，…，βlr∈{α，2α，…，nα}∪{qsα，(1+qs)α，…，(n+qs)α}

使得βli≠βlj(i≠j)，且gli(z)(?0)，i=1，2，…，r滿足σ(gli)

H1(z)=a*+g*(z)eβzs

(2.8)

其中β(≠0)為復常數，g*(z)(?0)為整函數且滿足σ(g*)

gl1(z)eβl1zs+…+glr(z)eβlrzs-g*(z)eβzs-a*=0

(2.9)

若β≠βlj，j=1，2，…，r，則由引理2.2和(2.9)式可得

gli(z)≡0，i=1，2，…，r，g*(z)≡0，a*≡0

矛盾。

若存在j∈{1，2，…，r}使得β=βlj，則(2.9)式可以表示成

(2.10)

由引理2.2和(2.10)式可得

glj(z)-g*(z)≡0，gli(z)≡0，i≠j，a*≡0

矛盾。因此，H1(z)沒有有窮Borel例外值。

由情形1和情形2可知，H1(z)取任意c∈{0}無窮多次，且滿足λ(H1-c)=σ(f)。

定理1.1證畢。

定理1.2的證明使用與定理1.1類似的證明方法，分以下四種情形進行證明。

情形1設qs=1，m=1，則由(2.1)～(2.3)式可得

(2.11)

又因為f(qz+η)?f(z)，所以g(qz+η)h(z)?g(z)，且由α≠2α≠…≠(n+1)α，g(z)h(z)?0，σ(g)

H2(z)=h1(z)eαzs+h2(z)e2αzs+…+hn+1(z)e(n+1)αzs

(2.12)

其中hi(z)，i=1，2，…，n+1是關于g(z)，g(qz+η)，h(z)的微分多項式且滿足σ(hi)

情形1.1當a=α1時，由(2.11)式和(2.12)式可得

H2(z)=hn+1(z)e(n+1)αzs

又由P(f)(f(qz+η)-f(z))?0可知hn+1(z)?0。因此，當qs=1，m=1，a=α1時，0為H2(z)的Borel例外值。

情形1.2當a≠α1時，記

則(2.11)式可以寫成

P(f)(f(qz+η)-f(z))=A1(z)eαzs+A2(z)e2αzs+…+An+1(z)e(n+1)αzs

顯然，Ai(z)?0，σ(Ai)

使用與定理1.1中情形2類似的證明方法，易知當qs=1，m=1，a≠α1時，H2(z)沒有有窮Borel例外值。

情形2設qs=1，m≠1，則

(2.13)

情形2.1若存在i∈{1，2，…，m}使得a=αi，不失一般性，設a=α1，則由(2.13)式可得

B1(z)e(n1+1)αzs+B2(z)e(n1+2)αzs+…+

Bn-n1+1(z)e(n+1)αzs

H2(z)=ht1(z)e(n1+1)αzs+ht2(z)e(n1+2)αzs+…+htn-n1+1(z)e(n+1)αzs

其中hti(z)，i=1，2，…，n-n1+1是關于g(z)，g(qz+η)，h(z)的微分多項式且滿足σ(hti)

使用與定理1.1中情形2類似的證明方法，易知當qs=1，m≠1，且存在i∈{1，2，…，m}使得a=αi時，H2(z)沒有有窮Borel例外值。

情形2.2若a≠αi，i=1，2，…，m，則由(2.13)式可得

使用與定理1.1中情形2類似的證明方法，易知當qs=1，m≠1，a≠αi，i=1，2，…，m時，H2(z)沒有有窮Borel例外值。

情形3設qs≠1，m=1，則

P(f)(f(qz+η)-f(z))=an(a-α1+g(z)eαzs)n(g(qz+η)h(z)eqsαzs-g(z)eαzs)

(2.14)

情形3.1若a=α1，則由(2.14)式可得

P(f)(f(qz+η)-f(z))=ang(z)ng(qz+η)h(z)(n+qs)αzs-ang(z)n+1e(n+1)αzs

由qs≠-1，-2，…，-n，1，g(z)h(z)?0，σ(g)

H2(z)=hv1(z)e(n+qs)αzs+hv2(z)e(n+1)αzs

其中hvi(z)，i=1，2是關于g(z)，g(qz+η)，h(z)的微分多項式且滿足σ(hvi)

使用與定理1.1中情形2類似的證明方法，易知當qs≠1，m=1，a=α1時，H2(z)沒有有窮Borel例外值。

情形3.2若a≠α1，則由(2.14)式可得

(2.15)

(a) 若qs-1不是整數，則iα≠(j+qs)α，i=1，2，…，n+1，j=0，1，…，n。由g(z)h(z)?0，σ(g)

(b) 若qs-1是整數，因為qs-1≠0，-1，所以分以下兩種情形進行證明。

若qs-1≥1，則對(2.15)式重排得到

P(f)(f(qz+η)-f(z))=-an(a-

α1)ng(z)eαzs+…+ang(z)ng(qz+

η)h(z)e(n+qs)αzs

由α≠(n+qs)α≠iα，i=2，3，…，n+1，α≠(n+qs)α≠(j+qs)α，j=0，1，…，n-1和g(z)h(z)?0，σ(g)

若qs-1≤-2，則對(2.15)式重排得到

P(f)(f(qz+η)-f(z))=an(a-α1)ng(qz+η)h(z)eqsαzs+…-ang(z)n+1e(n+1)αzs

由qsα≠(n+1)α≠iα，i=1，2，…，n，qsα≠(n+1)α≠(j+qs)α，j=1，2，…，n和g(z)h(z)?0，σ(g)

結合情形(a)和(b)，在(2.15)式中合并同類項，得到

使用與定理1.1中情形2類似的證明方法，易知當qs≠1，m=1，a≠α1時，H2(z)沒有有窮Borel例外值。

情形4設qs≠1，m≠1，則

(2.16)

情形4.1若存在i∈{1，…，m}使得a=αi，不失一般性，設a=α1，則由(2.16)式可得

使用與情形3.2類似的證明方法，易知當qs≠1，m≠1，且存在i∈{1，…，m}使得a=αi時，H2(z)沒有有窮Borel例外值。

情形4.2若a≠αi，i=1，2，…，m，則由(2.16)式可得

使用與情形3.2類似的證明方法，易知當qs≠1，m≠1，a≠αi，i=1，…，m時，H2(z)沒有有窮Borel例外值。

由情形1～4可知，H2(z)取任意c∈{0}無窮多次，且滿足λ(H2-c)=σ(f)。

定理1.2證畢。