格上篩法研究現狀與發展趨勢*

畢 蕾,路獻輝,3,王鯤鵬

1.中國科學院 信息工程研究所 信息安全國家重點實驗室,北京 100093

2.中國科學院大學 網絡空間安全學院,北京 100049

3.密碼科學技術國家重點實驗室,北京 100878

1 引言

格密碼近年來廣受關注.由于量子計算機的迅速發展,一些經典模型下的困難問題在量子計算環境下變得可以被有效求解.如果大規模的量子計算得以實現,現有的公鑰密碼安全將受到巨大的威脅和挑戰.因此,許多國家的政府和研究機構已逐步發起了在量子計算模型下安全的公鑰密碼算法,即后量子公鑰密碼的研發工作.格密碼由于在安全性、公私鑰尺寸、計算速度上的優勢,以及抵抗量子攻擊的能力,是其中最受矚目的類型之一.2020年,NIST后量子密碼算法標準征集的第三輪7個方案中有5個是基于格構造的,格密碼在未來有望替代RSA等現行公鑰密碼算法成為新一代的公鑰密碼標準.

格理論最初在密碼學中是一種分析工具,曾被用于分析背包密碼體制、RSA密碼體制等[1,2].1996年,Ajtai[3]開創性地給出了格中唯一最短向量問題(unique shortest vector problem,uSVP)在worstcase下到小整數解(small integer solutions,SIS)問題在average-case下的歸約證明,即這些困難問題在最壞情況下的困難性可以歸約到一類隨機格中問題的困難性,因此基于格的密碼體制可以提供最壞情況下的可證明安全性.

1997年,Ajtai-Dwork[4]首次將其作為一種設計工具,構造了第一個具有可證明安全的基于格的公鑰密碼體制AjtaiDwork,該方案的安全性基于格上唯一最短向量問題(unique shortest vector problem,uSVP)的困難性.此外,初期的格密碼方案還有NTRU密碼體制[5]、GGH密碼體制[6]等.這一時期的格密碼方案由于存在密鑰尺寸過大或者缺乏嚴格的安全性證明等缺陷,無法滿足實際應用的需求.

2005年,格密碼理論取得突破性進展—Regev[7]提出了基于帶錯誤的學習(learning with errors,LWE)問題的公鑰加密算法,大幅度縮小了密文和密鑰尺寸,同時又將加密算法的安全性歸約到了格上最壞情況困難問題的難解性—在量子歸約下,它至少與worst-case下的最短向量問題(shortest vector problem,SVP)的變體一樣困難.此后,LWE問題在格密碼方案的設計中得到了廣泛的應用.研究者們基于LWE問題提出了許多格密碼方案,如加密[8]、數字簽名[9]、密鑰交換[10]、全同態加密[11]等.

目前,大部分格密碼方案是基于帶錯誤學習(learning with errors,LWE)問題和NTRU假設構造的,而LWE和NTRU都可以用SVP求解算法進行求解,因此SVP求解問題的算法對于分析這些格密碼方案的實際安全性至關重要.

1.1 最短向量問題

求解SVP的常用算法是BKZ算法,在使用BKZ算法求解SVP時,需要將SVP精確求解算法嵌入BKZ算法的每一個基本模塊作為子程序,最終輸出最短向量的近似解.使用BKZ算法進行實際安全性分析,并將其中內嵌的精確SVP求解算法的復雜度作為算法總的時間復雜度的評估方式稱為coreSVP方法,這種方法是目前應用最廣泛的格密碼具體安全性評估方法.

SVP精確求解算法主要有以下四類:枚舉(enumeration)[12]、篩法(sieving)[13]、基于voronoi的方法(voronoi-based approach)[14]和離散高斯抽樣(discrete Gaussian sampling)[15].其中可實用化的有枚舉和篩法.枚舉的時間和空間復雜度分別為2ω(n)和poly(n),而篩法的時間和空間復雜度均為2Θ(n),其中n是格的維度.相比于枚舉算法,篩法的時間復雜度更低,因此是目前實用化格密碼算法實際安全性評估中主要使用的SVP精確求解算法.

1.2 篩法求解SVP

篩法是在2001年由Ajtai-Kumar-Sivakumar[13]首次提出的,稱為AKS篩法(AKS Sieve).AKS篩法求解SVP可分為三個步驟:首先生成指數級別的格向量,然后對這些向量進行篩選,在每一輪篩選中,將這些向量按照一定的規則遍歷、約化,使得向量的長度越來越短,最終得到一定數量的長度為O(λ1(Λ))的格向量,最后將這些向量兩兩相減,即可得到格中最短向量s∈Λ∧||s||=λ1(Λ).按照這一思路構造的篩法統稱為AKS類篩法.

除AKS類篩法外,還有另一類構造思路不同的篩法,稱為MV類篩法.這類篩法的初始列表是一個空列表,在算法過程中不斷抽取格向量并使用已經在列表中的向量對其進行約化,再約化后的向量添加至列表中,重復此過程直至找到格中最短向量.第一個MV類篩法是由Micciancio-Voulgaris[16]提出的列表篩法(ListSieve).

AKS篩法和列表篩法都是理論算法,即它們的正確性和復雜度都有嚴格的理論證明,并不依賴任何啟發式假設.但為了證明它們的正確性,算法中使用了一些隨機擾動技術,這種技術使算法本身效率很低,因此理論算法很難在實際中使用.基于這兩種理論算法,研究者們又提出了它們所對應啟發式版本—NV篩法(NV Sieve)[17]和高斯篩法(Gauss Sieve)[16].啟發式算法去掉了擾動技術,并引入了一些啟發式假設,使得算法丟失了對于正確性和復雜度的理論保障,但是在實際使用時更加高效.

據此,我們可將現有篩法按篩取的方式不同以及是否依賴啟發式假設分為四大類,如圖1所示1圖中數組(c t,c s)表示算法的時間復雜度和空間復雜度為和.下文中的復雜度表示中2cn亦指2cn+o(n).該圖中未標識出減秩篩法,因為該類算法著重于實際應用,并未在復雜度層面對算法進行優化..近十年來,研究者們對這四類篩法中的基本算法進行了各種改進(如表1所示),主要目標是優化篩法中的遍歷過程.Pujol-Stehlé[18]指出利用生日悖論可降低AKS篩法和列表篩法最后一個步驟中需要的長度為O(λ1(Λ))的向量的數目,從而降低算法的空間和時間復雜度.

表1 篩法技術分類Table 1 Sieving algorithms classified by technique

圖1 篩法發展歷程Figure 1 process of sieving

Wang-Liu-Tian-Bi[19]和Zhang-Pan-Hu[20]提出的層次篩法(Level Sieve)以NV篩法為起點,將篩法的每一輪分為多個層次進行,使得算法從遍歷所有向量變成先劃分大區域,再在大區域中進行分別遍歷和約化,使得算法所需遍歷向量數目減少,時間復雜度降低.Bai-Laarhoven-Stehlé[21]提出的元組篩法(Tuple Sieve)以列表篩法為基礎,在約化向量時每次約化多個向量而非僅僅兩個,這使算法需要的初始格向量個數減少,從而降低了算法的空間復雜度.之后,Herold-Kirshanova[22]和Herold-Kirshanova-Laarhoven[23]對元組篩法中尋找短向量的過程給出了更快的算法.Mukhopadhyay[24]提出的線性篩法(Linear Sieve)將之前篩法用球形區域劃分空間的方式換為用超立方體,從而降低了搜索向量進行約化得時間.另外,局部敏感哈希技術[25]、局部敏感過濾技術[26]以及量子Grover搜索算法[27]都被用來加速篩法中遍歷搜索的過程.從實際執行效果層面,漸進式篩法[9]、子篩法[28]和G6K[29]利用減秩技術對篩法的實際執行效果進行了優化,其中G6K是目前分析密碼安全性的主要實際工具.

發展到現在,篩法理論算法的時間和空間復雜度已經由最初的(25.9n,22.95n)(AKS篩法[13])降低到了(22.49n,22.49n)(線性篩法[24]). 啟發式算法中復雜度最低的經典算法是Becker-Ducas-Gama-Laarhoven[26]提出的LD篩法,它的時間和空間復雜度為(20.292n,20.208n),復雜度最低的量子算法是Laarhoven[30]提出的量子篩法,它的時間和空間復雜度為(20.265n,20.208n).目前coreSVP方法分析格方案的具體安全性時的經典和量子復雜度來源即為LD篩法和量子篩法.本文主要描述篩法發展過程中的重要思想和關鍵技術,總結目前存在的主要問題,并展望將來的發展方向.

1.3 組織結構

本文剩余的內容安排如下.第2節介紹相關的基礎知識.第3節和第4節介紹篩法的四個類別,其中第3節介紹AKS篩法和NV篩法,第4節介紹列表篩法和高斯篩法.接下來的章節按照時間順序介紹各種改進的方法.第5節介紹生日-AKS篩法和生日列表篩法.第6節介紹層次篩法.第7節介紹使用LSH/LSF技術的篩法.第8節介紹元組篩法.第9節介紹減秩篩法.第10節介紹量子加速篩法.第11節介紹線性篩法.第12節總結篩法當前存在的主要問題和未來的發展趨勢.

2 預備知識

2.1 符號

在本文中,符號Z和R表示整數集合和實數集合.標準漸進函數O(·)、Ω(·)、Θ(·)、o(·)、ω(·)定義如下:f(n)=O(g(n))意為存在正整數c和n0,對于所有n≥n0有f(n)≤c·g(n);f(n)=Ω(g(n))意為存在正整數c和n0,對于所有n≥n0有g(n)≤c·f(n);f(n)=Θ(g(n))意為既有f(n)=O(g(n))又有f(n)=Ω(g(n));f(n)=o(g(n))意為對于任意正數c,存在n0使得對于所有n≥n0有f(n)≤c·g(n);f(n)=ω(g(n))意為對于任意正數c,存在n0使得對于所有n≥n0有f(n)≥c·g(n).符號poly(x)表示關于變量x的任意未指定多項式函數.向量用小寫黑體字母表示(例如x),矩陣用大寫黑體字母表示(例如X).符號||·||表示向量的二范數?2,或稱歐式范數.符號dist(a,b)表示a和b之間的歐式距離.符號B n(x,r)表示一圓心為x,半徑為r的n維球,符號B n(r)=B n(0,r).

2.2 格和格上困難問題

定義1(格)已知Rm中的n個線性無關的行向量b1,b2,···,b n(m≥n),這組向量的所有整系數線性組合的集合稱為Λ,記為

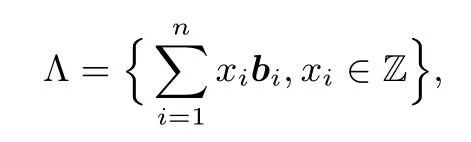
其中線性無關的向量組b1,b2,···,b n(m≥n)稱為格Λ的一組基,n為格的秩,m為格的維數.當m=n時,稱Λ為一個滿秩格.格Λ上的最短向量的范數記為λ1(Λ)=minv∈Λ{0}||v||.

定義2(最短向量問題,shortest vector problem,SVP)給定格Λ,尋找一個格向量u∈Λ{0}使得||u||=λ1(Λ).

3 AKS篩法和NV篩法

篩法是Ajtai-Kumar-Sivakumar于2001年首次提出的,稱為AKS篩法[13].其基本思想是首先生成一定數量的格向量,讓它們通過一系列越來越“細”的篩子,使得留下來的向量長度越來越短,最終找到最短的那一個.由于其龐大的空間開銷,算法一直未能實用化.直到2008年,Nguyen-Vidick基于AKS篩法提出了第一個篩法的啟發式算法NV篩法[17],可以應用于維度小于50的格,篩法才開始走向實用化.下面分別介紹AKS篩法和NV篩法.

3.1 AKS篩法

AKS篩法算法可分成三個步驟.首先,從一個較大的范圍B n(2O(n)O(λ1(Λ)))中抽取2O(n)個格向量.然后,通過一系列“篩取”的過程,輸出一定數量的B n(O(λ1(Λ)))中的格向量.最后,將得到的B n(O(λ1(Λ)))中的格向量兩兩相減并輸出最短的那個,即可以接近1的概率得到格中的最短向量.

“篩取”的過程是AKS篩法的核心,也是時間復雜度最高的部分.“篩取”的過程分多輪進行,每一輪輸入集合L?Λ∩B n(R)中的向量,輸出盡可能多的Λ∩B n(γR)中的向量,其中γ∈(0,1)稱為收縮系數.具體地,在一輪篩法中,從輸入集合L中選擇一個子集C作為“中心”,集合C滿足如下兩個性質:第一,集合C中任意兩個向量之間的距離都大于γR,即對于任意的v1,v2∈C,有||v1?v2||>γR;第二,對于中心之外的每個向量w∈LC,都存在C中的一個向量v,使得||w?v||≤γR,即w?v∈Λ∩B n(γR).因此,LC?Λ∩B n(R)中的每個向量對應一個Λ∩B n(γR)中的輸出向量.在每一輪篩取結束后,集合C中的向量將被丟棄.由于集合C中任意兩個向量之間的距離都大于γR,并且C?B n(R),這兩個條件保證了每一輪丟棄的向量的數目不會太多.

為了保證“篩取”結束后輸出的B n(O(λ1(Λ)))中的格向量是不同的,AKS篩法算法還引入了擾動(perturbation)技術.具體地,在算法的第一步中,首先從B n(ξλ1(Λ))中隨機抽取向量x,其中ξ>0.5是選定的擾動系數.為了能夠最終找到格中的最短向量,擾動不能太大,一般會選擇ξλ1(Λ)=O(λ1(Λ)).對每個隨機抽取的向量x,可找到基本區域中的向量y,使得v=y?x是一個格向量.由于向量y在基本區域中,有||y||≤R0:=nmaxi||b i||.因此,||v||≤R0+ξλ1(Λ).在第二步的“篩取”過程中,給定許多對(v,y)?Λ×B n(R),其中||v?y||≤ξλ1(Λ),算法會輸出(v′,y′)?Λ×B n(γR+ξλ1(Λ)),并保持||v′?y′||=||v?y||≤ξλ1(Λ).在執行線性多次“篩取”之后,即可以得到B n(O(ξλ1(Λ)/(1?γ)))中的格向量.當選擇合適的γ和ξ之后,Ajtai-Kumar-Sivakumar證明,算法會以很高的概率輸出長度O(λ1(Λ))的非零格向量.AKS篩法詳見算法1.

算法1 AKS篩法Input:Λ,γ,ξ,N Output:A shortest vector ofΛ 1 R0←n max i||b i||;2 L←Sampling(Λ,ξ,N,R0); ?算法2 3 R←R0;4 for j=1 to k do ?k表示算法3執行的輪數,由R,γ,ξ定義得到5 L←Sieving(L,R,γ); ?算法3 6 R←γR+ξλ1(Λ);7 end 8 find v0∈Λs.t.||v0||=min{||v?v′||where(v,y)∈L,(v′,y′)∈L,v?=v′};9 return v0.算法2 AKS篩法中的Sampling子算法Input:Λ,ξ,N,R0 Output:A set{(v i,y i,i∈[1,n])}?Λ×B n(R0)and y i?v i is uniformly distributed in B n(ξ)1 for i=1 to N do$←B n(ξλ1(Λ));3 v i←ApproxCVP(?x i,Λ); ?ApproxCVP指Babai’s rounding算法4 y i←v i+x i;5 end 6 return{(v i,y i,i∈[1,n])}.2 x i算法3 AKS篩法中的Sieving子算法Input:A set L={(v i,y i,i∈I)}?Λ×B n(R)and?i∈I,||y i?v i||≤ξλ1(Λ),R,γ Output:A set L′={(v′i,y′i,i∈I′)}?Λ×B n(γR+ξλ1(Λ))and?i∈I′,||y′i?v′i||≤ξλ1(Λ)1 C←?;2 for i∈I do 3 if?c∈C s.t.||y i?v c||≤γR then L′←L′∪{(v i?v c,y i?v c)}5 end 6 else 4 C←C∪{i}8 end 9 end 10 return L′.7

3.2 NV篩法

在AKS篩法中,為了使算法的輸出結果和復雜度有理論保障,算法引入了擾動技術.但這一技術在算法的實際執行中的作用并不顯著.當把擾動去掉,而直接在格點上進行操作時,可以使算法的執行更高效.基于這樣的想法,Nguyen-Vidick[17]提出了AKS篩法的啟發式版本——NV篩法.這樣得到的啟發式算法執行效率高,但無法保證一定可以得到格中的最短向量,也無法直接給出復雜度的界的證明.

與AKS篩法相似,NV篩法也分成三個步驟(見算法4).首先,用Klein近似最近平面算法算法抽取N個格向量放入集合L中.然后進行“篩取”,在每一輪的“篩取”過程中,長度在γR以內的向量直接通過“篩取”進入下一輪,而其他長度大于γR的向量將按照與AKS篩法中相同的方法,通過選取“中心”集合C得到剩下的長度在γR以內的向量.重復這一“篩取”的過程直到某一輪中所有通過“篩取”的向量都是零向量.最后,輸出最后一輪“篩取”之前所有向量中長度最小的向量.

算法4 NV篩法Input:Λ,2/3<γ<1,N Output:A short non-zero vector ofΛ 1 L←?;2 for j=1 to N do 3 L←L∪v sampled by using Klein’s randomized nearest plane algorithm;4 end 5 remove all zero vectors from L;6 L0←L;7 repeat 8 L0←L;9 L←Sieving(L,γ); ?算法5 10 remove all zero vectors from L;11 until L=?;12 compute v0∈L0 s.t.||v0||=min{||v||,v∈L0};13 return v0.算法5 NV篩法中的Sieving子算法Input:A set L?Λ∩B n(R)and shrinking factor 2/3<γ<1 Output:A set L′?Λ∩B n(γR)1 Set R←max v∈L||v||;2 initialize L′←{}and C←{0};3 for each v∈L do 5 4 if||v||≤γR then L′←L′∪{v}6 end 7 else if?c∈C s.t.||v?c||≤γR then L′←L′∪{v?c}9 end 10 else 8 11 C←C∪{v}12 end 13 end 14 return L′.

NV篩法算法中最重要的參數是初始輸入向量的數目N和收縮系數γ.當參數γ確定后,最終輸出的格向量的長度只與算法執行的輪數相關,輪數越多則最終得到的格向量越短.而算法會在所有初始抽取的N個向量用完之后結束,因此算法輪數受限于每輪算法執行時損失的向量數目.而算法執行過程中向量損失的主要來源是被用于作為“中心”.因此衡量“中心”集合的規模|C|對于確定參數和分析復雜度至關重要.為了分析|C|,Nguyen-Vidick使用了如下假設,并在低維度的實驗中對其合理性進行了驗證.

假設1令C n(γ,R)={x∈Rn,γR≤||x||≤R},假設L∩C n(γ,R)中的向量是均勻分布的.

實驗證明,NV篩法在維度小于50的格上可以正常使用.但由于空間復雜度過高,致使在格的維度超過50之后,就很難再將其實用化.

4 列表篩法和高斯篩法

2010年,Micciancio-Voulgaris[16]提出了一種新的篩法理論算法,稱為列表篩法,并給出了對應的啟發式版本,稱為高斯篩法.與AKS篩法和NV篩法在一開始就先生成大量格向量不同,列表篩法和高斯篩法從一個空列表L開始,逐步抽取和約化得到更短的格向量加入列表,直到找到滿足條件的短向量.

4.1 列表篩法

列表篩法算法使用列表L儲存每一輪生成的格向量.每一輪算法隨機抽取一個格向量,用列表L中的向量對其進行約化,使它盡可能地短,約化之后將其放進列表L中,已經在L中的向量不再改變或移除.當約化得到的向量長度小于等于μ(目標短向量長度),即可作為最終的結果輸出.詳見算法6.

算法6列表篩法Input:Λ,μ,N Output:v∈Λ∧||v||≤μor⊥1 Initialize a list L={0};2 for i=1 to N do 6 if?w∈L s.t.||v?w||<μthen 3 (v,p)←sampling(Λ,ξ,μ); ?算法7 4 (v,p)sieving((v,p),L); ?算法8 5 if v/∈L then 7 return v?w;8 end L←L∪{v};10 end 11 end 12 return⊥.9

算法7列表篩法中的Sampling子程序Input:Λ,ξ,μOutput:(v,p)∈Λ×R n 1 e$←B n(ξμ);2 p←e modΛ;3 v←p?e;4 return(v,p).

算法8列表篩法Sieving子程序Input:(v,p),L Output:reduced pair(v,p)1 while?w∈L s.t.||p?w||≤||p||do 2 (v,p)←(v?w,p?w)3 end 4 return(v,p).

接下來分析列表L長度的上界,從而得到時間與空間復雜度.算法終止前每一輪得到的約化后的向量與L中已有的向量均距離較遠(至少為μ).根據這一性質,利用球填充(sphere packing)問題的分析結果,可給出|L|的上界,據此可以得到算法的空間復雜度.算法的每一輪需要使用新抽取的向量與L中的所有向量進行兩兩組合計算,因此算法時間復雜度的上界約為|L|2.

在上面的分析中存在一個問題:算法的某些輪得到的向量可能已經存在于L中,即發生了“碰撞”.當遇到這種情況,算法既浪費了時間,又沒有得到更短的向量.因此在分析算法的時間復雜度時,需考慮這樣的事件發生的概率.為此,列表篩法和AKS篩法一樣,采用了“擾動”技術.在抽取格點v時,實際抽取的是一對向量e,p,再計算v=p?e,其中e滿足||e||≤ξμ,這里ξ>0.5.這樣得到的向量,滿足v在B n(p,ξμ)中均勻分布,且B n(p,ξμ)中包含多于1個格向量的概率大于0.因此,當B n(p,ξμ)中包含兩個距離小于等于μ的格向量時,抽到其中一個向量兩次的概率和同時抽到這兩個向量的概率相同.據此,可以得到發生碰撞的概率的上界.可以看出,當ξ增大時,|L|上升,但發生碰撞的概率降低,反之亦然.因此ξ的選擇對于算法最終的復雜度至關重要.

4.2 高斯篩法

高斯篩法是列表篩法的啟發式版本(詳見算法9),它與列表篩法的區別在于,在抽取了一個隨機的格向量v并對其進行長度上的約化時,列表篩法只利用列表L中的向量對于v進行約化,而高斯篩法還利用v對L中已存在的向量進行約化.當這個過程結束后,列表中的所有向量都是兩兩互相約化的,即

?w1,w2∈L:||w1±w2||≥max{||w1||,||w2||}.

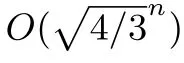
算法9高斯篩法Input:Λ,μOutput:v∈Λ∧||v||≤μ1 Initialize a list L={0}and a stack S=?;2 repeat v←v?w;6 end 7 while?w∈L s.t.||w||>||v||∧||w?v||≤||w||do 3 Get a vector v from S(or sample a new one);4 while?w∈L s.t.||w||≤||v||∧||v?w||≤||v||do 5 8 L←L{w};S←S∪{w?v};10 end 11 if v has changed then 9 12 S←S∪{v}(unless v=0);13 end 14 else L←L∪{v};15 until v satisfying||v||≤μ;

除了約化方式的不同,高斯篩法還去掉了列表篩法中的擾動技術,因此高斯篩法的時間復雜度并沒有一個可以證明的上界,但可以估計時間復雜度大約為將列表中的向量兩兩組合檢查否可以互相進行約化的時間,因此時間復雜度大約為列表長度的平方級別,即O((4/3)n).

5 生日-AKS篩法和生日-列表篩法

2011年,Pujol-Stehlé[18]提出,利用生日悖論(birthday paradox)可降低篩法成功找到最短向量所需的向量總數,因此可以降低算法的復雜度.Pujol-Stehlé對AKS篩法和列表篩法進行了優化,優化得到的算法分別稱為生日-AKS篩法(AKS Sieve-birthday)和生日-列表篩法(ListSieve-birthday).

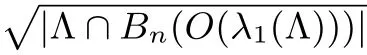
由于使用生日悖論結論時需要集合中的向量是互相獨立同分布的,但AKS篩法的最后一個部分中的向量并不滿足這個條件,因此需要對算法進行一些調整.可以證明這些調整帶來的開銷很小,對于整體復雜度的下降沒有影響[32].

6 層次篩法

2011年,Wang-Liu-Tian-Bi提出了一種的新的啟發式算法—兩層篩法(Two-Level Sieve)[19],在這一新的框架下,之前的NV篩法可視作一層篩法(One-Level Sieve).之后在2013年,Zhang-Pan-Hu通過進一步改進兩層篩法的結構對算法進行優化,提出了三層篩法(Three-Level Sieve)[20].通過使用多層篩的技術,層次篩法以增加空間復雜度為代價降低了算法的時間復雜度.

6.1 兩層篩法

Wang-Liu-Tian-Bi提出,可以將原始的NV篩法看作一層篩法,那么兩層篩法即為利用“兩層篩”的技術.具體地,算法的每一輪分為兩層:第一層首先將C n(γ2R)={x∈Rn:γ2R≤||x||≤R}中的格向量劃分進不同的半徑為γ1R的大球中(γ1>1),所有大球需覆蓋C n(γ2R);第二層再將每個大球中的格向量劃分進不同的小球中(詳見算法10).可以看出,對于每個格向量,一層篩的大球數目較少,二層篩時只需與已確定的大球內部的小球中心點相比較即可,因此減少了比較時間,降低了時間復雜度.但同時,由于需要存儲的向量數量變多,導致空間復雜度上升.

算法10兩層篩法Input:A set S?Λ∩B n(R)and shrinking factors√2/3<γ2<1<γ1<√2γ2 Output:A set S′?Λ∩B n(γ2 R)1 Set R←max v∈S||v||;2 Initialize S′←{}and C1←{0},C2←{0};3 for each v∈S do 4 if||v||≤γ2 R then S′←S′∪{v};6 end 7 else 5 8 if?c∈C1 s.t.||v?c||≤γ1 R then 9 if?c′∈C c2 s.t.||v?c′||≤γ2 R then 10 S′←S′∪{v?c′};11 end 12 else C c2←C c2∪{v};13 end 14 else 15 C1←C1∪{v};16 C2←C2∪{C v2={v}};17 end 18 end 19 end 20 Return S′.

6.2 三層篩法

三層篩法的思路和兩層篩法類似,采用了“三層篩”的技術,以增大空間復雜度為代價,進一步降低了算法的時間復雜度.

一個自然的問題是,是否可以繼續增大層次的數目來降低算法的時間復雜度.對此,文獻[20]指出,這種想法是可行的,但由于這樣做的技術難度越來越高,而收益卻越來越低,所以沒有繼續的必要.之后,Laarhoven在詳細分析了兩種層次篩法的復雜度后,給出了k層篩法(k-Level Sieve)的算法框架和空間、時間復雜度的分析方式[30].

算法11三層篩法Input:A set S?Λ∩B n(R)and shrinking factors 0.88<γ3<1<γ2<γ1<√2γ3 Output:A set S′?Λ∩B n(γ3 R)1 Set R←max v∈S||v||;2 initialize S′←{}and C1←{0};3 for each v∈S do 4 if||v||≤γ3 R then S′←S′∪{v};6 end 7 else 5 8 if?c1∈C1 s.t.||v?c1||≤γ1 R then 9 if?c2∈C c12 s.t.||v?c2||≤γ2 R then 10 if?c3∈C c1,c23 s.t.||v?c3||≤γ3 R then 11 S′←S′∪{v?c3};12 end 13 else C c1,c23 ←C c1,c23 ∪{v};14 end 15 else C c12←C c12∪{v};16 end 17 else 18 C1←C1∪{v};19 end 20 end 21 end 22 return S′.

7使用LSH/LSF技術的篩法

2015年,Laarhoven[25]提出使用局部敏感哈希(locality-sensitive hashing,LSH)技術對篩法中窮搜的部分進行加速,并在高斯篩法上進行了實現,改進后的算法稱為哈希篩法(HashSieve).相比于高斯篩法,哈希篩法在保持空間復雜度不變的基礎上降低了時間復雜度.

LSH有許多不同的類型,哈希篩法使用的是角(angular)LSH,在這之后,Laarhoven-Weger[33]以及Becker-Laarhoven[34]又分別提出了利用球(sphere)LSH和正軸體(cross-polytope)LSH加速的篩法球篩法(SphereSieve)和正軸體篩法(CPSieve).球篩法和正軸體篩法又進一步降低了哈希篩法的時間復雜度.

2016年,Becker-Ducas-Gama-Laarhoven[26]提出使用一種與LSH類似的、稱為局部敏感過濾(locality-sensitive filters,LSF)的技術對篩法進行加速,改進后的算法稱為LD篩法(LDSieve).相比于使用LSH技術的三個算法,LD篩法的空間復雜度不變,時間復雜度更低.

7.1 LSH和LSF技術

LSH.LSH是用來解決最近鄰搜索(near(est)neighbor searching,NNS)問題的一項技術.正式地,最近鄰搜索問題定義為:

定義3(最近鄰搜索問題,near(est)neighbor searching,NNS)給定一列n維的向量L={w1,w2,···,w N},對于一個目標向量v/∈L,找到一個w∈L使得它是L中離v最近的向量.

顯然,這個問題可以通過遍歷列表L解決.但當列表L規模較大時,這樣做的時間復雜度很高.而使用LSH技術可以降低解決問題的時間復雜度.正式地,LSH函數簇H有性質如下:

定義4對任意v,w∈Rn,一簇函數H={h:Rn→N}對于測度D有如下性質:

(1)如果D(v,w)≤r1,那么Prh∈H[h(v)=h(w)]≥p1,

(2)如果D(v,w)≥r2,那么Prh∈H[h(v)=h(w)]≤p2,那么稱H對于測度D是(r1,r2,p1,p2)-敏感的.

根據定義4,如果有p1?p2,那么可使用H以不可忽略的概率區分在測度D下與v距離至多r1和至少r2的向量.

具體地,使用LSH技術時,首先從哈希簇H中隨機選擇t×k個哈希函數.之后,構造t個哈希表T1,T2,···,T t,每個表T i中使用由k個哈希函數組合得到的哈希函數組,表示為h i.對每個w∈L,計算它的t個哈希值h1(w),h2(w),···,h t(w),并根據每個哈希值h i(w)將w存放在哈希表T i中相應的位置.那么,當給定目標向量v后,計算它的t個哈希值h i(v),將每個哈希表中與之發生碰撞的所有w∈L取出作為一個集合,這個集合即為離v較近的向量的集合.之后,再遍歷這個集合中尋找離v最近的向量即可.

考慮圖2中一個使用角LSH技術的實例:給定列表L={w1,w2,···,w10}和目標向量v,要求找到L中距離v最近的向量.該實例中使用3個哈希表,每個表中使用k=2個超平面來劃分空間(即為選定的哈希函數),因此使用2k=4個哈希桶存放相應哈希值的向量.可以看出,使用多個哈希表可以使得靠近目標點的向量盡可能地不被遺漏.對于每個哈希表(即每種空間劃分的方式),首先對L中的向量計算哈希值(即落在平面中的哪個區域)并存放在相應的哈希桶中.之后,計算v的3個哈希值,與每個哈希表相比對,將與之哈希值相同的向量取出并存儲,留待最后遍歷時使用.在該實例中,最終得到的與v距離較近的向量的集合為C={w6,w7,w8,w9,w10}.那么在尋找離v最近的向量時,遍歷集合C即可.

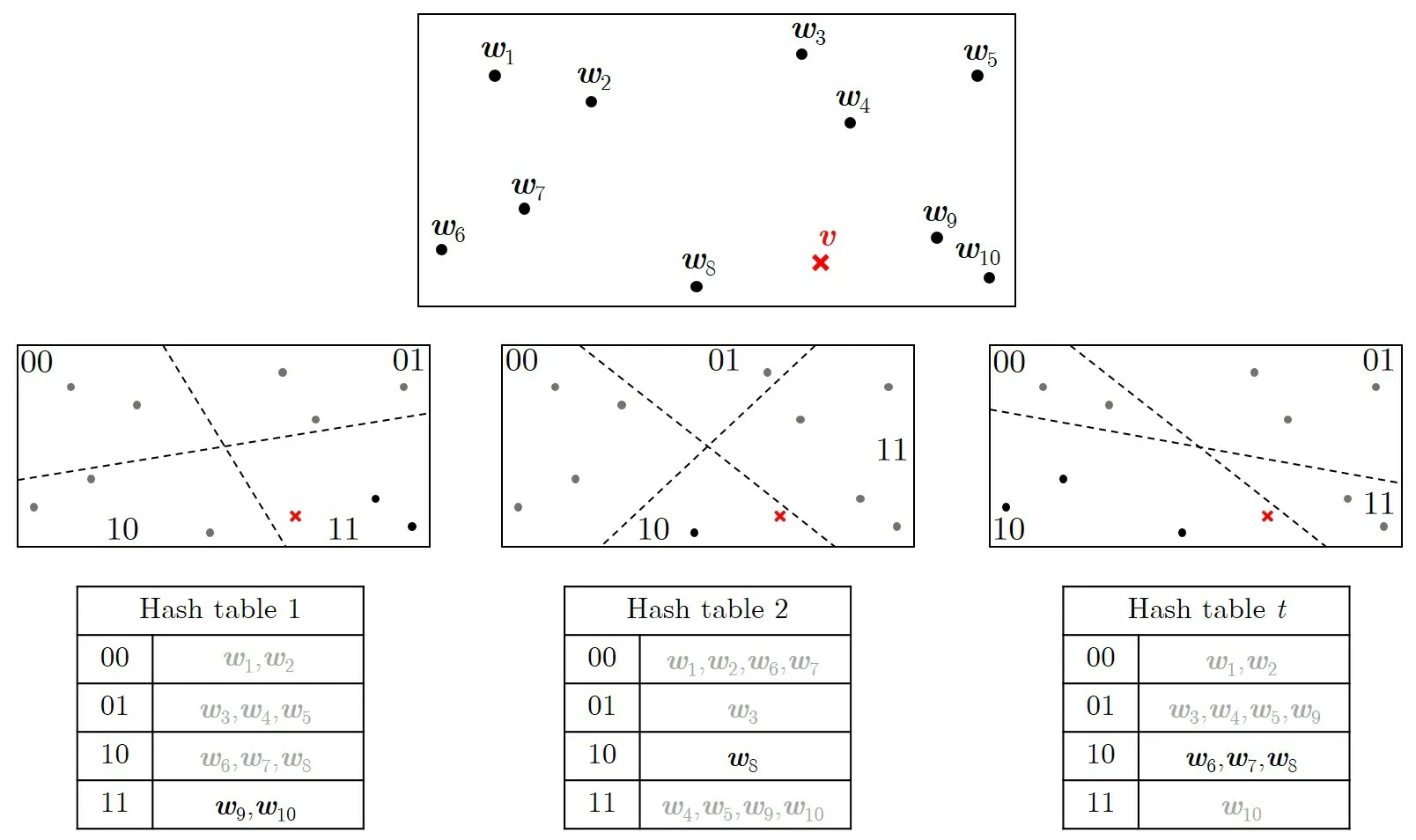
圖2 局部敏感哈希實例Figure 2 Example of locality-sensitive hash

顯然,算法解決NNS問題的效率取決于對哈希簇和參數k、t的選擇.

?哈希簇:根據選擇的哈希簇不同,目前在使用的LSH技術主要可分為:角(angular)LSH(或稱超平面(hyperplane)LSH)、球(sphere)LSH、正軸體(cross-polytope)LSH.其中角LSH的理論分析較差但算法運行非常高效,球LSH的理論非常完善但不具備實際操作性.而正軸體LSH則同時具備了以上兩個算法的優點:它既有充分的理論保障,在實踐中又比角LSH效果更好.

?參數k和t:當選擇較大的k和t時,可以將區分“近”和“遠”的概率差放大(定義4中的p1?p2),這樣可以使篩選出的“較近”的元素的集合較小,最終的比較次數較少,但另一方面,這樣做會使得哈希表較長,需要的存儲空間較大.因此,需要選擇合適的參數k和t來平衡算法的時間和空間復雜度.

LSF.對于LSF技術來說,每個過濾函數的輸出是二元的,即通過或沒有通過這個過濾函數.因此對于一個列表L,當它經過過濾函數f之后得到的集合L f?L中包含所有通過這個過濾函數的向量.L f中的向量在對應的測度下距離較近.

當利用這樣的過濾函數來解決NNS問題時,首先給定一個過濾函數的分布F,再抽取t×k個過濾函數f i,j∈F.將每k個進行組合,構造t個過濾函數組f i.對于w,通過過濾函數組f i意味著通過了其中的所有k個過濾函數f i,j,j=1,2,···,k.那么對于列表L,相應地存在t個過濾輸出集合L1,L2,···,L t.最后,當輸入一個目標向量v時,用t個過濾函數組對v進行檢測,對于那些v可以通過的過濾函數組f i,將它對應的L i中的向量全部集合在一起,即為離v較近的向量的集合.再從這個集合中遍歷尋找離v最近的向量即可.

7.2 哈希篩法

哈希篩法是利用角(angular)LSH技術對高斯篩法進行優化得到的.具體地,角LSH技術是指在LSH中使用角距離(angular distance)來進行距離的度量:對于向量v和w,它們的角距離定義為

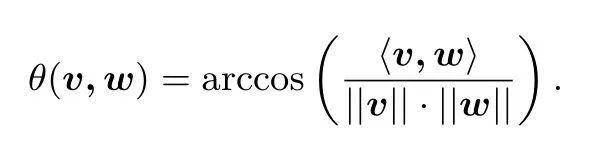
在這樣的度量方式下,當兩個向量的夾角小時即可認為它們的距離較近,反之亦然.

為了使用角LSH來優化高斯篩法,需要對高斯篩法中的約化條件做一些相應的調整.高斯篩法中的約化條件可寫作:

用u2約化u1:如果||u1±u2||<||u1||,那么u1←u1±u2.

根據這樣的約化方法,可以使得得到的列表L中的向量都是兩兩約化的,即對于?w1,w2∈L均滿足||w1±w2||≥max{||w1||,||w2||}.從這個條件可以得到?w1,w2∈L均滿足夾角至少為π/3.據此可以得到一個弱化版的約化條件:

用u2約化u1:如果θ(u1,u2)<π/3并且||u1||≥||u2||,那么u1←u1±u2.

為了分析約化的過程和算法的復雜度,需作如下假設:

假設2隨機抽取的向量v,w之間的夾角θ(v,w)和從Rn中的單位球面上隨機抽取的兩個向量v′,w′之間的夾角θ(v′,w′)服從相同的分布.

在高維空間中,已知隨機抽取的兩個向量之間的夾角以較大的概率等于π/2.因此在假設2成立時,有?w1,w2∈L,θ(w1,w2)以很大的概率接近π/2.另一方面,由弱化的約化條件可知,當兩個向量可以用其中一個對另一個進行約化時,意味著它們之間的夾角是小于π/3的,而約化之后的夾角一定是大于π/3的,為了簡化分析,假設約化之后的向量之間的夾角均為π/2.

利用這些信息,即可定義角LSH所需的函數簇:

直觀地,每個a可定義一個如圖2實例中的虛線(超平面).而對于v,w,Pr[h(v)?=h(w)]可利用它們之間的角度進行計算:

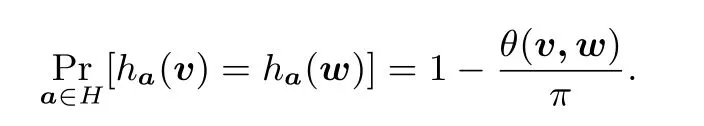
算法12哈希篩法Input:Λ,μOutput:v∈Λ∧||v||≤μ1 Initialize a list L={0}and a stack S=?;2 initialize t hash tables T i;3 sample k·t random hash vectors a i,j;4 repeat 5 Get a vector v from S(or sample a new one);6 obtain the set of candidates C=∪ti=1 T i[h i(v)];7 while?w∈C s.t.||w||≤||v||∧||v?w||≤||v||do v←v?w;9 end 10 while?w∈C s.t.||w||>||v||∧||w?v||≤||w||do 8 11 L←L{w};12 T i←T i{w}for all t hash tables;13 S←S∪{w?v};14 end 15 if v has changed then 16 S←S∪{v}(unless v=0);17 end 18 else 19 L←L∪{v};20 T i[h i(v)]←T i[h i(v)]∪{v}for all t hash tables;21 end 22 until v satisfying||v||≤μ;

7.3 球篩法

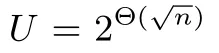
算法13球篩法Input:A set S?Λ∩B n(R)and shrinking factor 2/3<γ<1 Output:A set S′?Λ∩B n(γR)1 initialize S′←{}and C←{0};2 initialize t empty hash tables T i;3 sample k·t random spherical hash functions h i,j∈H;4 for each v∈S do 5 if||v||≤γR then S′←S′∪{v};7 end 8 else 6 9 obtain the set of candidates C=∪ti=1 T i[h i(±v)];10 for each w∈C do 11 if||v?w||≤γR then 12 S′←S′∪{v?w};13 continue the outermost loop;14 end 15 end 16 T i[h i(v)]←T i[h i(v)]∪{v}for all i∈[t];17 end 18 end 19 return S′.

7.4 正軸體篩法

正軸體篩法是利用正軸體(cross-polytope)LSH技術對高斯篩法進行優化得到的啟發式算法[34].正軸體是一類任意維均存在的凸多胞體(如圖3是一個三維正軸體),由標準基向量{e i∈Rn}作為頂點定義而成.根據正軸體定義的哈希函數可寫作

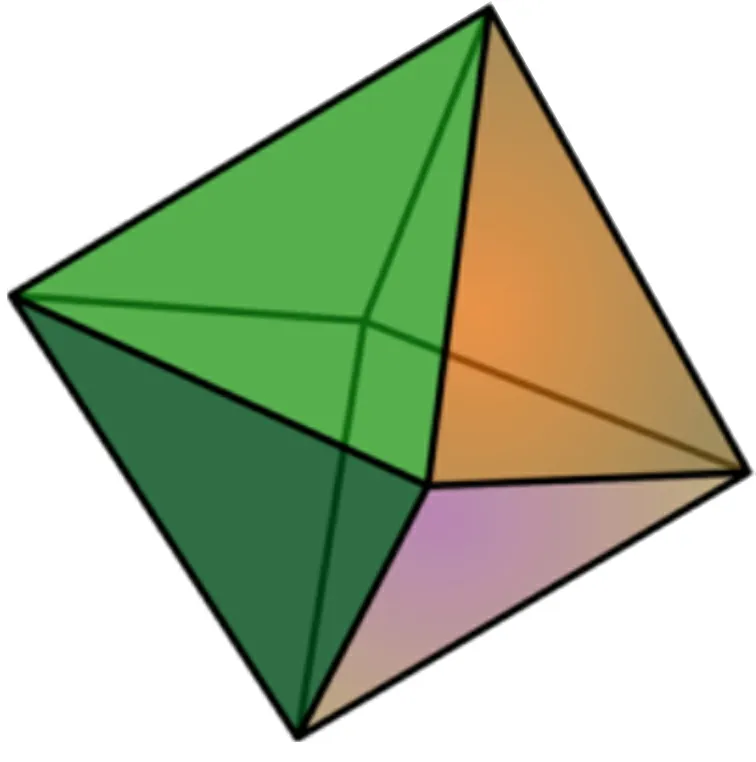
圖3 三維正軸體Figure 3 3-orthoplex

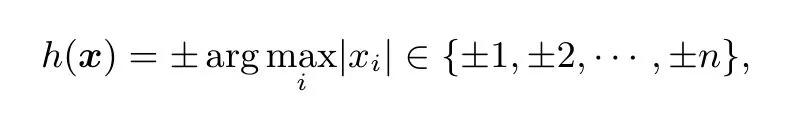
其中符號與絕對值最大的分量的符號一致.例如對于v=(3,?5)有h(v)=?2.

但這樣只定義了一個哈希函數,因此我們需要引入一個隨機變換,使得它能夠成為一個函數簇.令分布A輸出矩陣A=(a i,j)∈Rn×n,其中對于任意的i,j有a i,j～N(0,1),即一個標準正態分布.這樣即可定義哈希函數簇

H={h A:h A(x)=h A(A x),A～A}.

之后,將這個哈希函數簇在GaussSieve上應用即可得到新的算法CPSieve(見算法14).

算法14正軸體篩法Input:Λ,μOutput:v∈Λ∧||v||≤μ1 initialize a list L={0}and a stack S=?;2 sample t×k random Gaussian matrices A i,j;3 define h i,j(x)=h(A i,j x)and h i(x)=(h i,1(x),h i,2(x),···,h i,k(x))initialize t hash tables T i;4 sample k·t random hash vectors a i,j;5 repeat 9 6 get a vector v from S(or sample a new one);7 obtain the set of candidates C=∪ti=1 T i[h i(v)]∪∪ti=1 T i[h i(?v)];8 while?w∈C s.t.||w||≤||v||∧||v?w||≤||v||do v←v?w;10 end 11 while?w∈C s.t.||w||>||v||∧||w?v||≤||w||do 12 L←L{w};13 T i←T i{w}for all t hash tables;14 S←S∪{w?v};15 end 16 if v has changed then 17 S←S∪{v}(unless v=0);18 end 19 else 20 L←L∪{v};21 T i[h i(v)]←T i[h i(v)]∪{v}for all t hash tables;22 end 23 until v satisfying||v||≤μ;

7.5 LD篩法

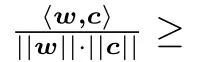
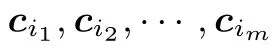
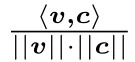
8 元組篩法

2016年,Bai-Laarhoven-Stehlé指出,現有篩法都只考慮了兩個向量之間的相互約化,而實際上可以每次約化多個向量[21].根據這樣的思想,他們提出了基于列表篩法的新的啟發式篩法——元組篩法(Tuple Sieve),或稱k-篩法(k-Seive),其中常數k表示每次約化時考慮的向量個數.相比于之前的篩法,元組篩法以增加時間復雜度為代價,降低了算法的空間復雜度,在一定程度上緩解了篩法由于空間復雜度過大而不能應用于實際的問題.之后,Herold-Kirshanova[22]和Herold-Kirshanova-Laarhoven[23]進一步將尋找約化后的短向量的過程看作一個k-列表問題(k-list problem),并給出了更快的算法.

8.1 BLS-元組篩法

BLS-元組篩法的每次約化中考慮k個向量.首先考慮k=2的情況,這時的算法稱為雙篩法(DoubleSieve).算法的每一輪將一組B n(R)內的向量通過兩兩約化得到一組B n(γR)內的向量(見算法15).具體地,在每輪中,算法首先將范數小于γR的向量從列表L中去掉、直接進入下一輪,使得列表L中只包含了范數在(γR,R)范圍內的向量.然后,對列表L中的每一對向量w,v,如果||v±w||≤γR,則將v±w加入到下一輪的列表中.

下面分析雙篩法的時間與空間復雜度.由于算法在約化時所考慮的向量v,w∈L都在(γR,R)范圍內,如果γ≈1時,那么||v||≈||w||≈R.此時,事件||v?w||<γR等價于w∈B(R)∩B(v,γR).為了計算該事件發生的概率,需要做如下假設:

假設3在雙篩法(算法15)中,假設對于?v∈L,v/||v||可看作是從單位球面上的均勻分布中抽取的獨立同分布的向量.

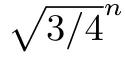
k=3時的算法稱為三篩法(TripleSieve,算法16),它與k=2時的區別在于每次約化時使用3個向量,即v±w±x.因此,此時在球覆蓋時不只考慮單個的向量,而也會考慮兩個向量的和或差也是否也可以覆蓋一部分球面.例如,如果有||v?w?x||≤γR,那說明x∈B(R)∩B(v?w,γR).直觀上,這也解釋了為了什么k=3的情況下覆蓋整個球面所需的向量個數比k=2時更少.與雙篩法類似,在三篩法的分析中也需要做與假設3類似的假設:

假設4在三篩法(算法16)中,假設對于?v∈L,v/||v||可看作是單位球面上均勻隨機抽取的的獨立同分布向量,且?v?=w∈L,v±w中范數最小的向量可看作一個隨機向量.

算法15雙篩法Input:L?B n(R),γ,R Output:L′?B n(γR)1 L′←{};2 for each v∈L do 3 if||v||≤γR then 4 L′←L′∪{v};L←L{v};6 end 7 end 8 for each v,w∈L do 5 9 if||v±w||≤γR then 10 L′←L′∪{v±w};11 end 12 end 13 return L′

算法16三篩法Input:L?B n(R),γ,R Output:L′?B n(γR)1 L′←{};2 for each v∈L do 4 L′←L′∪{v};3 if||v||≤γR then L←L{v};6 end 7 end 8 for each v,w,x∈L do 5 9 if||v±w±x||≤γR then 10 L′←L′∪{v±w±x};11 end 12 end 13 return L′

對于更大的k,Bai-Laarhoven-Stehlé指出,算法的時間和空間復雜度可以歸納為k n(1+o(1))和k n/k(1+o(1)).當k趨近于n時,算法的時間和空間復雜度分別趨近于n n+o(n)和n1+o(1).因此,參數k平衡了算法時間復雜度和空間復雜度,逐漸增大k的過程即可視為用時間換空間的過程.

8.2 HK-元組篩法

2017年,Herold-Kirshanova[22]繼續發展了元組篩法.他們指出,當把利用篩法求解SVP的每一輪看作k列表問題之后,Bai-Laarhoven-Stehlé[21]只是對所有的可能解進行了遍歷去尋找滿足條件的那些,而實際上這個過程可以進一步進行優化.具體地,一個近似k列表問題可以歸約到滿足一定性質的結構問題上,而這樣的結構問題可以被更快速地解決.因此,可以利用解決這個結構問題的算法來對現有的元組篩法加速.更進一步地,這樣的結構問題還可以與LSH技術相結合,得到一個擴展版的結構問題,Herold-Kirshanova也同樣給出了解決這個問題的算法,并把它們一起用在了加速元組篩法上.

下面首先給出近似k-列表問題,結構以及結構問題的定義,然后分析近似k列表問題的解與結構問題的解的關系,最后給出解決結構問題的算法(算法17).

定義6(結構,configuration)對于k個向量x1,x2,···,x k∈S n?1,其中S n?1表示單位球面,結構C=Conf(x1,x2,···,x k)定義為這k個向量的Gram矩陣,即C i,j=〈x i,x j〉,i,j∈[k].

定義7(結構問題,configuration problem)輸入k個指數量級的列表L1,L2,···,L k,其中的元素取自S n.對于一個給定的目標結構C和?>0,輸出k元組(x1,x2,···,x k)∈L1×L2×···×L k,使其對于所有的i,j∈[k]均滿足|〈x i,x j〉?C i,j|≤?.

根據定義可知,若選擇目標結構C滿足∑i,j C i,j≤t2,那么C對應的結構問題的解(x1,x2,···,x k)滿足〈x i,x j〉≈C i,j,?i,j,因此||∑i x i||2≈∑i,j C i,j≤t2,即(x1,x2,···,x k)也是以t為目標的近似k-列表問題的解.因此,任意一個滿足∑i,j C i,j≤t2的結構C對應的結構問題的解都包含在以t為目標的近似k-列表問題的解當中.但反過來,后者所有的解可能需要多個不同的結構問題的解才能完全覆蓋.

篩法的每一輪要求輸入列表和輸出列表的規模基本一樣,因此需要找到盡可能多的近似k-列表問題的解.為了求解盡可能少的結構問題同時得到盡可能多的近似k-列表問題解,Herold-Kirshanova選擇只求解包含最多解的結構問題.具體地,結構問題可較容易地確定輸出解的數目和目標結構C之間的關系:給定|L|k個可能的元組作為輸入,目標是輸出|L|個元組,它們滿足方程|L|k·det(C)n/2=|L|.根據上述方程,選擇det(C)最大的C可使結果達到最優,即在輸入數目固定的情況下最大化輸出列表規模.

算法17 k-list for the configuration problem Input:L1,L2,···,L k,C,? Output:List L of k-tuples(x1,x2,···,x k s.t.|〈x i,x j〉?C i,j|≤?for all i,j 1 L←{};2 for all x1∈L1 do 3 for all j=2,3,···k do j ←FILTER(x1,L j,C(1,j),?); ?算法18 5 end 6 for all x2∈L(1)2 do 4 L(1)7 L(2)j ←FILTER(x2,L(1)j,C(2,j),?); ?算法18 8···9 for all x k∈L(k?1)k do 10 L←L∪{(x1,x2,···,x k)};11 end 12 end 13 end 14 return L.算法18 FILTER Input:x,L,c,? Output:L′1 L′←{};2 for all x′∈L do 3 if|〈x,x′〉|≤γR then 4 L′←L′∪{x};5 end 6 end 7 return L′.

8.3 HKL-元組篩法

2018年,Herold-Kirshanova-Laarhoven[23]提出可以將近似k列表問題約化到的結構問題略做調整以使得問題能夠被更加快速地解決,并且可以結合LSF技術來對算法整體進行加速.

具體地,文獻[22]選擇使用det(C)最大的C對應的結構問題,以最大化每一輪輸出元組的數目.而Herold-Kirshanova-Laarhoven指出某些結構C雖然det(C)不是最大的,但它們可以使輸出元組的搜索更加快速.為了保持對于輸出元組數目的要求,就需要增加輸入列表的大小.對此,Herold-Kirshanova-Laarhoven給出了對應的關系和分析,并給出了如何找到最優的C來平衡算法的時間和空間.

9 減秩篩法

減秩(rank reduction)技術是一種格上常用的解決困難問題的技術,當求解n維格上的困難問題時,可以首先解決一個n?k維的子格上的問題,利用求解得到的結果再來解決原問題.

2018年,Laarhoven-Mariano[9]提出了利用減秩技術的漸進式篩法(Progressive Lattice Sieving).具體地,對于一個n維格上的SVP,首先在一個低維度的子格上進行篩法,然后逐漸向其中添加其余維度上的基向量,并在此過程中繼續篩的過程,直到所有的基向量都添加完畢并找到了完整格上的最短向量為止.減秩技術幾乎可以與所有篩法相結合使用,Laarhoven-Mariano提出的漸進式篩法主要考慮了與高斯篩法和哈希篩法這兩種效率較高的篩法進行結合,結果顯示利用這種方法,可將篩法提速20-40倍.除此之外,由于漸進式篩法的大部分算法過程是在子格中進行,因此算法的空間復雜度更低.

同年,Ducas[28]提出了子篩法(SubSieve),也可以看作是使用了減秩技術.Ducas證明只需要在少于n?k維的格上調用數次篩法,即可解決原格上的SVP,其中k=Θ(n/logn).子篩法對于算法總體的時間、空間復雜度的優化是亞指數級別的,但在實際執行中比其他篩法在70-80維的實驗中快10倍.

2019年,基于這兩種利用了減秩技術的篩法,Albrecht-Ducas-Herold等人[29]提出了一種開源的抽象的狀態機——G6K(General Sieve Kernel),是目前分析密碼安全性的主要實際工具.利用這個狀態機可以實際地解決格上的SVP.具體地,Albrecht-Ducas-Herold等人利用G6K解決了Darmstadt SVP挑戰2https://www.latticechallenge.org/svp-challenge.中的151維SVP,時間比之前的記錄快了400倍.之后,在2021年,Ducas-Stevens-Woerden又利用G6K解決了180維的SVP挑戰,是目前Darmstadt SVP挑戰的最高紀錄.

10 量子加速篩法

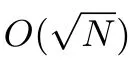
10.1 量子篩法

文獻[30,35]給出了一些啟發式篩法在利用Grover算法加速后的時間、空間復雜度(見表2),其中效果最好的是基于LDSieve的量子篩法(Quantum Sieve).

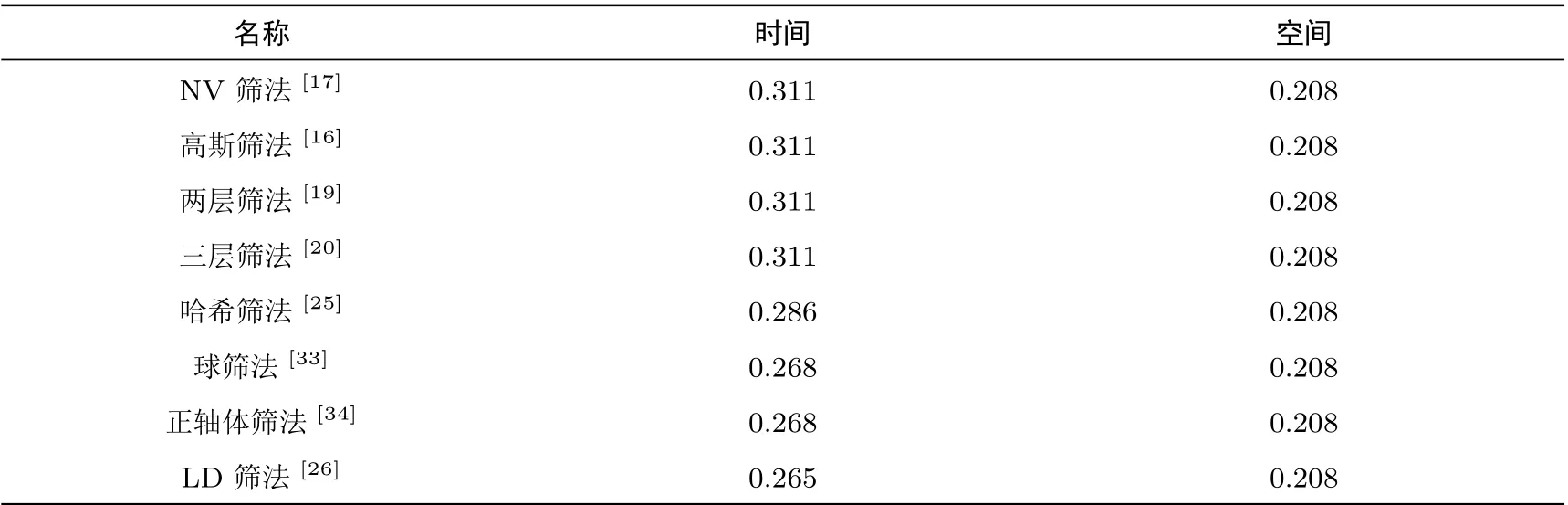
表2 部分啟發式篩法的在量子算法加速下的空間、時間復雜度Table 2 Space&time complexity of some heuristic sieving algorithms sped up by using quantum algorithm

10.2 量子元組篩法

2019年,Kirshanova-M?rtensson-Postlethwaite-Roy Moulik[31]提出了元組篩法的量子加速版本.具體地,在解決元組篩法中所引入的結構問題(見第8.2節)時,需要對許多元組進行遍歷并判斷它們是否滿足給定的目標,這一遍歷過程可以使用量子Grover搜索算法進行加速.另外,經典的元組篩法在解決結構問題時使用了LSH/LSF技術進行加速,而Grover搜索算法也可與這兩項技術結合使用.這是因為在使用這兩項技術尋找合適的元組時,是將所有元組按照一定的結構進行分類,之后再選擇其中的一些類進行搜索而非全部遍歷,這一過程也可利用量子Grover搜索算法進行加速.

11 線性篩法

2019年,Mukhopadhyay[24]基于AKS篩法的框架,提出了一個新的可證明的篩法.新篩法的時間復雜度與空間復雜度是線性關系(之前是平方關系),因此算法命名為線性篩法(Linear Sieve).

AKS Sieve中的一個關鍵步驟就是對于一個在B n(R)抽取得到的向量y,找到離它最近的中心向量c.這個問題可以看作一個NNS問題(見第7節),可利用LSH和LSF技術解決,但這兩項技術的使用都依賴于一些啟發式假設,因此不能用于優化可證明的篩法.AKS Sieve的解決方式是在B n(R)中構造很多半徑為γR的小球,將空間劃分為一些小區域,之后對每個向量y,在由所有的球心組成的中心集合中尋找是否存在一個球心c使得||y?c||≤γR.如果不存在這樣的球心,就將這個y對應的格點v加入中心集合成為一個新的球心.

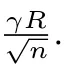
這樣做降低了算法的時間復雜度,但同時也增加了算法的空間復雜度.這是因為AKS Sieve中的每個中心點之間的距離都是大于γR的,而當用超立方體劃分時會有一些中心之間的距離是小于γR的,因此中心的數目會比之前更多.但可以證明即使是這樣,算法的時間復雜度依然比AKS Sieve低.

12 結論

自Ajtai-Kumar-Sivakumar于2001年提出第一個篩法以來,研究者們對篩法進行了大量深入的研究,不僅提出了不同的算法框架,而且通過借鑒其他領域相關問題的技術,提出了許多不同的改進方法,降低了算法的復雜度.本文對目前主要的篩法進行了分類,并梳理了它們之間的關系和發展脈絡.

盡管篩法在過去二十多年取得了許多進展,但目前的篩法仍然存在空間復雜度過高、理論與實際效果相差較大[36]等缺點.在實際應用中,篩法只能在低維度的格上進行實驗,距離高維度、大規模使用仍然存在一定的差距.由于篩法對于格密碼方案的實際安全性分析至關重要,解決篩法在高維格上的應用問題,可以極大地推進格密碼分析領域的發展.因此,對于篩法的進一步研究無論是從理論角度還是從實用角度都具有十分重要的價值和意義.

基于目前的研究現狀,未來我們還可以在以下幾個方面對篩法進行更加深入的研究:

?深化量子加速:目前利用量子算法對于篩法加速還停留在簡單地替代篩法中窮搜的階段,如何更加充分和深入利用量子算法對篩法進行加速尚不可知,這是我們在量子篩法領域需要考慮的問題.

?混合算法:混合算法的框架在格困難問題的求解中是一種常見的思路,而目前大多數篩法都是單獨使用,如何與其他算法相結合是未來一個重要的研究方向.例如,2019年Guo-Johansson-M?rtensson-Wagner[37]提出將篩法與BKW算法相結合用來解決LWE問題. 2020年Doulgerakis-Laarhoven-Weger[38]提出將篩法作為一個子程序、與枚舉以及切片等技術相結合的算法,該算法比直接使用篩法有更低的時間和空間復雜度.

?借鑒其他領域的技術:在目前對于篩法的改進中,借鑒其他領域的技術是一個重要的工具(例如局部敏感哈希技術),如何利用更多不同領域的想法和技術對篩法進行優化,是未來需要繼續考慮的問題.例如,2019年Laarhoven[39]指出了人工智能領域中演化算法(evolutionary algorithm)的部分技術與篩法領域中近年來所發展技術的相似性,并進一步利用演化算法中其他的技術對篩法進行改進.