基于RLWE困難假設的NTRU型代理重加密方案*
王 超,韓益亮,段曉巍,李 魚
武警工程大學 密碼工程學院,西安 710086
1 引言
大數據時代的到來、云計算的飛速發展以及數據平臺跨域聯合體系的構建,對云安全提出了更高層次的需求,單一的公鑰加密體制難以滿足大數據云安全的發展需要.隨著代理重加密的出現,半可信代理作為中間方,對密文數據進行代理轉換,有效解決了電子文件安全分發、跨域信息傳輸、云數據安全存儲等問題.近年來,量子算法深入發展,給基于傳統數學困難問題的密碼體制帶來了不可忽視的威脅,因此,對抗量子算法攻擊的實用化后量子密碼算法的需求日漸迫切.NTRU(number theory research unit)作為格密碼中最實用的密碼體制,在NIST后量子密碼算法標準化第三輪的評估中成功勝出,預示著NTRU有望成為標準化的實用后量子密碼算法.自2015年Nu?ez提出第一個基于NTRU的代理重加密方案[1]以來,其密鑰尺寸小、結構簡潔、計算高效的優勢有效推動了實用化后量子代理重加密算法的研究發展.
1996年,Hoffstein、Silverman和Pipher提出了NTRU公鑰加密體制[2],該體制基于NTRU格上的NTRU假設,雖然自提出至今還沒有有效的攻擊算法對此假設產生威脅,但該假設一直未能歸約到格上的經典困難問題,導致NTRU密碼體制長期缺乏形式化的安全性證明[3].2011年,Stehlé和Steinfeld[4]將私鑰采樣自格上的離散高斯分布提出了一個可證明安全的NTRU變體,其IND-CPA安全性可以歸約為RLWE困難問題,但是該方案對標準差參數要求過大,導致效率較低且實用性較差.2016年,NIST征集后量子密碼標準化算法以來,在第二輪評估中成功入圍公鑰加密算法的NTRU密碼體制共有兩個:NTRU[5](NTRUEncrypt[6]與NTRU-HRSS[7]的結合版)和NTRU-Prime[8],其中NTRU成為第三輪評估中成功入圍僅留的4個密鑰封裝(key encapsulation mechanism,KEM)算法之一,但以上三個方案中核心的公鑰加密(public key encryption,PKE)算法,都未能歸約到格上困難問題并提供嚴格的形式化安全性證明,僅能達到OW-CPA安全.2019年,Seck等[9]提出一種新型可證明安全的NTRU公鑰加密變體BI-NTRU-LPR,該方案是繼Stehle和Steinfeld對NTRU公鑰體制的安全性進行形式化歸約之后,對NTRU公鑰體制進行形式化安全性證明的最新嘗試,將私鑰和隨機多項式分別采樣自多項式環和RLWE(ring learning with errors)噪聲分布,最終將方案的IND-CPA安全性歸約到D-RLWE問題.
自2010年Xagawa[10]首次在格上構造了代理重加密方案以來,基于格的代理重加密體制逐漸代替基于傳統困難問題的代理重加密體制,成為研究的熱點問題.圍繞Xagawa方案雙向且不抗合謀以及如何使格基代理重加密方案更加實用化的問題,基于格的單一代理重加密方案[11-13]和與身份、屬性、條件、門限、區塊鏈等相結合的代理重加密方案[14-18]相繼被提出.目前基于格的代理重加密方案大都基于LWE困難假設,密鑰采樣算法為格上的高斯采樣算法或陷門生成算法采樣,其矩陣形式的密鑰尺寸較大、方案計算復雜度較高.而基于RLWE困難假設中的多項式環和錯誤分布采樣密鑰可以有效解決密鑰尺寸大的問題,另外通過快速傅里葉變換算法(fast Fourier transform,FFT)加速多項式乘法可以有效提升計算效率,降低計算復雜度.NTRU作為格密碼中最實用的密碼體制,隨著其IND-CPA安全性在RLWE困難假設下得到證明,基于可證明安全的NTRU變體構造密鑰尺寸小、實用性強的格基代理重加密體制具有重要的意義.2015年,Nu?ez首次提出了兩個基于NTRU的代理重加密方案[1]—NTRUReEncrypt和PS-NTRUReEncrypt,其中PS-NTRUReEncrypt方案在RLWE困難性假設下可以達到IND-CPA安全,但兩個方案都是雙向且不抗合謀的.2017年,Nu?ez等[19]總結了經典的格基代理重加密方案并給出了方案性能對比,在對比中NTRU代理重加密方案[1]較LWE型方案具有更實用的密鑰尺寸和計算復雜度優勢.2017年,Polyakov等[20]基于NTRU-RLWE和BV同態加密方案在RLWE困難假設下,提出兩個IND-CPA安全的單向抗合謀的代理重加密方案—NTRU-ABD-PRE和BV-PRE.2019年,張明武等[21]基于NTRUReEncrypt方案重新設計了重加密密鑰生成算法,提出了一個單向抗合謀的NTRU代理重加密方案,但該方案未能在格困難問題假設下進行形式化的安全性歸約.
本文主要研究NTRU公鑰和代理密碼體制的可證明安全性,構造IND-CPA安全的單向抗合謀的高效代理重加密方案.首先改進BI-NTRU-LPR公鑰加密方案,將雙密鑰結構簡化為單密鑰結構,設計一種在RLWE困難假設下達到IND-CPA安全的公鑰加密方案.結合文獻[21]提出的抗合謀重加密密鑰算法,構造出標準模型下可證明安全的單向抗合謀代理重加密方案.本文方案進一步完善了NTRU代理密碼體制,與已有的NTRU代理重加密方案相比,既保證了單向抗合謀的安全屬性又保證了方案的可證明安全性,且沒有增加計算復雜度和密鑰尺寸.與基于LWE的代理重加密方案相比,計算復雜度和密鑰尺寸更小,實用性更強.
2 相關知識
2.1 RLWE
RLWE分布:定義整系數多項式環為R=Z(x)/x n+1,其中n∈Z為2的冪次方,設R q=Zq(x)/x n+1是模為素整數q的多項式商環.在R q上隨機均勻選取多項式向量a和秘密值s,在χq上隨機均勻選取錯誤向量e,χq在R q上服從某種公開的特定分布,令b=as+e,則(a,b)為R q×R q上的RLWE分布A s,χ.
RLWE判定問題(D-RLWE):給定樣本分布(a,b),能否以不可忽略的優勢區分(a,b)為RLWE分布A s,χ和R q×R q上的隨機均勻分布.
2.2 單向代理重加密的系統定義
定義1根據文獻[21]可知一個單向代理重加密方案由授權者、代理者和被授權者等三個參與方和以下五個算法組成.
(1)初始化階段Setup(k):輸入安全參數k,輸出公共參數pp.
(2)密鑰生成算法KeyGen(pp):輸入公共參數pp,利用密鑰生成算法為用戶i生成公鑰pki和私鑰ski.
(3)加密算法Encrypt(pki,m):輸入授權者i的公鑰pki和明文m,輸出密文C i.
(4)重加密密鑰生成算法ReKeyGen(ski,pki,skj,pkj):輸入授權者i和被授權者j的密鑰ski,pki,skj,pkj,輸出重加密密鑰rki→j.
(5)重加密算法ReEncrypt(C i,rki→j):輸入密文C i和重加密密鑰rki→j,輸出被授權者j可解密的重加密密文C j.
(6)解密算法Decrypt(C j,skj):輸入重加密密文C j和被授權者j的私鑰skj,輸出明文m.
定義2單向代理重加密的正確性定義.
(1)對于密鑰生成算法生成的任意密鑰對(pki,skj)和明文空間中的任意明文m,都有下式成立:Decrypt(Encrypt(pki,m),ski)=m.
(2)對于重加密密鑰生成算法生成的任意密鑰rki→j和任意加密算法生成的密文C i以及任意明文m,都有下式成立:Decrypt(ReEncrypt(C i,rki→j),skj)=m.
2.3 單向代理重加密的IND-CPA安全模型
下面通過挑戰者和攻擊者Λ之間的安全游戲來定義本文方案的IND-CPA安全性,游戲共分為以下三個階段.
初始階段.挑戰者將安全參數k輸入Setup(),輸出公共參數pp,并將公共參數pp發送給Λ,根據Λ是否知道用戶的私鑰信息,將用戶分為誠實用戶(HU)和腐化用戶(CU).
學習階段.攻擊者Λ可以向挑戰者發起任意多項式次以下查詢
(1)私鑰查詢:Λ向挑戰者發起私鑰查詢,若查詢的用戶為腐化用戶,挑戰者返回給Λ相應的用戶私鑰ski,否則返回終止符⊥.
(2)重加密密鑰查詢:Λ向挑戰者發起用戶i到用戶j的重加密密鑰查詢,挑戰者運行ReKeyGen算法得到重加密密鑰rki→j,并將其返回給Λ.如果i=j或者用戶i為誠實用戶,用戶j為腐化用戶,則挑戰者忽略Λ的請求,返回一個隨機值.
(3)重加密查詢:Λ向挑戰者發起密文C i到密文C j的重加密查詢,挑戰者利用重加密密鑰rki→j運行ReEncrypt算法得到重加密密文C j,并將其返回給Λ.如果i=j或者用戶i為誠實用戶,用戶j為腐化用戶,則挑戰者忽略Λ的請求,返回一個隨機值.
挑戰階段.當Λ認為學習階段可以結束時,選擇兩個明文(m0,m1)和攻擊目標用戶i?(要求i?不能為腐化用戶)并提交給挑戰者,挑戰者隨機選擇一個隨機數d∈{0,1},然后返回用戶i?的加密密文C i?=Encrypt(pki?,m d)給Λ作為挑戰密文.
Λ在收到挑戰密文之后可以繼續發起學習階段中的私鑰查詢、重加密密鑰查詢、重加密查詢,要求是不能針對用戶i?,挑戰者應答的方式與上階段一致.
猜測.最后Λ停止查詢并輸出一個猜測值d′∈{0,1},如果d′=d則宣布Λ獲勝,其優勢為:
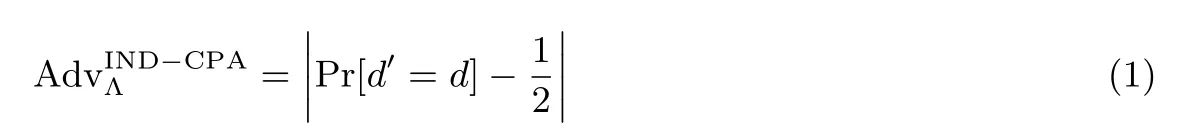
如果對于任意多項式時間攻擊者,攻擊者的優勢是可忽略的,則稱基于NTRU的單向代理重加密方案是IND-CPA安全的.
2.4 符號說明

3 NTRU型公鑰和代理重加密方案
3.1 NTRU公鑰加密變體
在嘗試基于BI-NTRU-LPR方案設計可證明安全的單向抗合謀代理重加密方案時,由于BI-NTRULPR方案的雙密鑰特性,使得該代理重加密方案的重加密密鑰尺寸擴張為PS-NTRUReEncrypt方案的兩倍,且重加密過程中噪聲擴張嚴重,方案解密正確率無法達到PS-NTRUReEncrypt方案中的正確界限1?n?ω(·).為了減小密鑰尺寸,實現低噪聲的代理重加密方案的設計,在本小節中,設計了一個單密鑰的IND-CPA安全的NTRU公鑰加密變體NTRU-LPR,方案的安全性可以歸約到D-RLWE困難問題,方案的加法運算為多項式加法,乘法運算為多項式卷積乘法.
(1)NTRU-LPR密鑰生成算法(KeyGen):從L t上隨機均勻的選取多項式B∈R q,從L t上隨機選取小系數多項式g∈R q(系數取為0、1和?1),g滿足以下兩個條件:g q·g≡1(modq),g≡1(modp),如果g不滿足條件則重新進行選取,從χq上隨機選取小系數多項式e′∈R q,計算公鑰pk為h=g q B+e′(modq),私鑰sk為g.
(2)NTRU-LPR加密算法(Encrypt):輸入公鑰pk=h,從明文空間M中選取明文m,從χq上選取兩個隨機多項式u,e∈R q,計算密文C=p(uh+e)+m.
(3)NTRU-LPR解密算法(Decrypt):輸入密文C和私鑰sk=g,計算C′=C·g(modq),解密得m=C′(modp).
(4)NTRU-LPR公鑰加密方案正確性分析:首先計算:
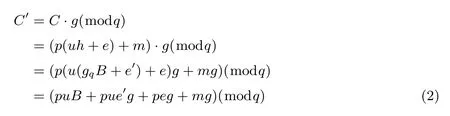
定理1當|puB+pue′g+peg+mg|∞ 證明:當|puB+pue′g+peg+mg|∞ 定理2根據文獻[9]中引理3和引理4可知,在選擇適當的參數t=3,αq≥n1/4,n3/2+3αqω(logn)pn1/2 本節基于上節提出的NTRU-LPR公鑰加密方案,結合文獻[21]提出的重加密密鑰生成算法,設計了一個基于NTRU的IND-CPA安全的單向抗合謀的代理重加密方案NTRU-LPR-ReEncrypt,具體方案如下: (1)初始階段(Setup):輸入安全參數k,選取多項式環R q=R/q R=Zq(x)/x n+1,n為2的冪 (2)密鑰生成算法(KeyGen):運行NTRU-LPR公鑰加密方案的密鑰生成算法,為授權者i生成一對密鑰(pki,ski)=(h i,g i),為被授權者j生成一對密鑰(pkj,skj)=(h j,g j). (3)加密算法(Encrypt):輸入授權者i的公鑰h i和明文m,從χq選取隨機多項式u,e i∈R q,計算密文C i=p(uh i+e i)+m(modq),并發送給代理者. (4)重加密密鑰生成算法(ReKeyGen):本算法基于文獻[21]提出的NTRU重加密體制的抗合謀交互式重加密密鑰生成算法.輸入授權者i和被授權者j的私鑰g i和g j,首先授權者從R q中選取一個隨機多項式f,從χq中選擇隨機多項式e j,計算f′=f(g i+pe j)(modq)發送給被授權者j,并將f發送給代理者,被授權者j收到f′后,計算f′′=f′g j q(modq)并發送給代理者,代理者收到f和f′′后,計算重加密密鑰rki→j為: (5)重加密算法(ReEncrypt):代理者運行重加密密鑰生成算法,輸入授權者i的密文C i和重加密密鑰rki→j,計算C j=C irki→j,將授權者i的密文C i轉換為被授權者的密文C j,并將C j發送給被授權者j. (6)解密算法(Decrypt):被授權者收到轉換密文C j后,輸入自己的私鑰g j,計算m′=C j g j(modq),最終得明文為m=m′(modp). 本節對NTRU-LPR-ReEncrypt方案的正確性、單向性、多跳性和抗合謀性進行分析,在D-RLWE困難問題下對方案的IND-CPA安全性進行形式化的安全性證明. 本節從方案的輸入面(授權者的解密正確性)和輸出面(被授權者的解密正確性)兩個方面進行分析. (1)由于NTRU-LPR-ReEncrypt方案是基于3.1節提出的NTRU-LPR設計的,輸入面授權者的解密正確率與NTRU-LPR方案的解密正確率一致,詳見3.1節. (2)對方案輸出面被授權者的解密正確性如下:被授權者接收到轉換密文C j后,計算: 當|puB+pue′g i+pe i g i+pug iq B pe j+pue′pe j+pe i pe j+pme j+mg i|∞ m′=puB+pue′g i+pe i g i+pug iq B pe j+pue′pe j+pe i pe j+pme j+mg i, 而后計算m=m′(modp),由于g i≡1(modp),最終可得m=m′,在選擇適當的參數t=3,αq≥n1/4,n3/2+αqω(logn)p(4n1/2+2p+pn3/2) 根據密文的轉換方向,代理重加密可以分為單向代理重加密和雙向代理重加密.單向代理重加密在實際應用中信息保密性更強,有效控制代理者的密文轉換能力,防止代理者未經自己同意向腐化用戶轉換密文信息造成信息泄漏.即代理者只能將Alice的密文轉換成Bob的密文或是將Bob的密文轉換成Alice的密文,而不允許雙向同時轉換.在NTRU-LPR-ReEncrypt方案中,由于噪聲多項式的存在,代理者無法將重加密密鑰rki→j=g i g j q+pe j g j q(modq)求逆或其它運算得到rkj→i,因此NTRU-LPR-ReEncrypt方案是一個單向代理重加密方案. 多跳性是指代理者多次運行重加密算法C j=C irki→j實現i從1取到N?1,j=i+1時,連續重加密得到重加密密文C N=C1rk1→2rk2→3···rkN?1→N,仍有Decrypt(C N,g N)=m(E表示剩余2N?1?1個提出因子p后的所有多項式). 解密C N過程如下: 經過驗證,代理者連續重加密N?1次得到的密文C N仍然可以解密出明文m,方案滿足多跳性. 本方案是滿足抗合謀性的,代理者與被授權者合謀不能得到授權者的私鑰信息,代理者與授權者合謀也不能得到被授權者的私鑰信息. 假設被授權者是一個腐化用戶,此時被授權者的私鑰g j對于代理者是透明的,代理者計算rki→j g j=(g i g j q+pe j g j q)g j(modq)=(g i+pe j)(modq),由于噪聲多項式pe j的存在,代理者無法獲得授權者的私鑰g i. 假設授權者是一個腐化用戶,此時授權者的私鑰g i對于代理者是透明的,代理者計算rki→j g iq=(g i g j q+pe j g j q)g iq(modq)=(g j q+pe j g j q g iq)(modq),由于噪聲多項式pe j g j q g iq的存在,代理者無法獲得被授權者的私鑰g j. 本小節證明NTRU-LPR-ReEncrypt方案在D-RLWE困難假設下是IND-CPA安全的. 學習階段.攻擊者Λ可向算法β查詢任意多項式次以下查詢 (1)私鑰查詢:攻擊者Λ向算法β發起私鑰查詢,若查詢的用戶不是攻擊目標用戶i?,算法β運行KeyGen算法返回給攻擊者相應的用戶私鑰g i,否則返回終止符⊥. (2)重加密密鑰查詢:攻擊者Λ向算法β發起用戶i到用戶j的重加密密鑰查詢,在私鑰查詢的基礎上,算法β運行ReKeyGen算法得到重加密密鑰rki→j=g i g j q+pe j g j q(modq),并將其返回給攻擊者Λ.如果i=j或者用戶i為誠實用戶,用戶j為腐化用戶,則挑戰者忽略攻擊者Λ的請求,返回一個隨機值. (3)重加密查詢:攻擊者Λ向算法β發起密文C i到密文C j的重加密查詢,算法β利用重加密密鑰rki→j運行ReEncrypt算法得到重加密密文C j=C irki→j,并將其返回給攻擊者Λ.如果i=j或者用戶i為誠實用戶,用戶j為腐化用戶,則挑戰者忽略攻擊者的請求,返回一個隨機值. 本節分為兩個小節對方案進行效率分析,5節對本文提出的公鑰加密變體NTRU-LPR方案進行效率分析,5.2節對基于NTRU-LPR構造的NTRU型代理重加密方案進行效率分析. 對比方案的參數選擇,不同的多項式采樣空間使方案具有不同的加密結構和安全性,目前NTRU體制的多項式采樣空間主要分為三種.傳統NTRU公鑰加密方案NTRU-HPS[5]及其變體NTRU-HRSS[7]的多項式采樣空間為R=Z(x)/x n?1,該采樣空間的方案在理論上還未能歸約到格上的困難問題,安全性僅能達到OW-CPA安全.NTRU prime[8]的多項式采樣空間為素數域R=Z(x)/x n?x?1,可最小化攻擊者可用的環同態數,與傳統NTRU公鑰加密方案一致,在理論上也未能歸約到格上的困難問題,僅能達到OW-CPA安全.RLWE型NTRU變體[4,9]的多項式采樣空間為R=Z(x)/x n+1,其IND-CPA安全性可以歸約為格上的RLWE問題.本方案為RLWE型NTRU變體,其安全性可以歸約為RLWE判定問題,具體對比如表1所示. 表1 NTRU公鑰加密變體參數選擇Table 1 Parameter selection of NTRU public key encryption variant 對比方案的密鑰尺寸和通信成本,與原BI-NTRU-LPR[9]相比,保證原有的IND-CPA安全性的同時,單密鑰的加密結構使通信成本和密鑰尺寸降低了50%,與NIST后量子密碼算法標準化提交的NTRU-HPS-DPKE[5]、NTRU-HRSS-DPKE[7]和NTRU prime core[8]方案相比,減小了私鑰尺寸并將安全性由OW-CPA安全提升為IND-CPA安全.與Stehlé和Steinfeld提出的第一個IND-CPA安全的NTRU公鑰加密變體[4]相比,私鑰尺寸減小了log2q倍,新方案的公鑰均勻性依賴于RLWE判定問題,在一定程度上解決了該方案通過密鑰采樣自離散高斯分布來保證IND-CPA安全性,造成對參數要求過大導致方案不實用的問題.具體對比如表2所示. 表2 NTRU公鑰加密變體性能對比Table 2 Parameter comparision of NTRU public key encryption variant 在安全屬性方面,與目前已知的NTRU代理重加密方案NTRUReEncrypt[1]、PS-NTRUReEncrypt[1]、張明武方案[21]和基于格上LWE問題構造的代理重加密方案[13,14]以及基于RLWE問題構造的NTRU-ABD-PRE方案[20]相比,本文方案將方案的困難性歸約為RLWE問題,并證明方案在RLWE困難假設下可以達到IND-CPA安全,同時方案滿足單向性、抗合謀性和多跳性,具體對比如表3所示. 在方案的密鑰尺寸方面,與NTRU體制的代理重加密方案相比,完善了代理重加密安全屬性的同時,沒有增加密鑰尺寸,保留了NTRU體制密鑰尺寸小的實用性優勢.與LWE體制的代理重加密方案相比,由于在文獻[14]中為保證方案的正確性,設置參數為m>6nlog2q,所以有m>n,O(mlog2q)>O(nlog2q),在文獻[13]中,設置參數為m>(5+3δ)nlog2q,同樣有m>n,O(mlog2q)>O(nlog2q),因此本文方案的密鑰尺寸遠小于LWE體制的代理重加密方案[13,14].與基于RLWE問題的NTRUABD-PRE方案[20]相比,將重加密密鑰尺寸減小為NTRU-ABD-PRE方案的1/log2q.具體對比如表4所示. 表4 漸近密鑰尺寸對比Table 4 Asymptotic key size comparison 在方案的計算復雜度方面,本文方案的核心運算的多項式環上的乘法運算,通過快速傅里葉變換算法FFT(fast Fourier transform)可以有效加快運算效率,使得方案計算復雜度為O(nlogn),而基于LWE體制的代理重加密方案中的運算為矩陣運算,加密、解密和重加密計算復雜度為O(n2),本文方案較LWE體制的代理重加密方案在計算復雜度方面具有較大優勢,與目前已有NTRU和RLWE體制的代理重加密方案相比,沒有增加方案的計算復雜度.具體對比如表5所示. 表5 計算復雜度對比Table 5 Computing complexity comparison 在方案的時間成本方面,定義多項式卷積乘法的時間成本為t m,隨機多項式的采樣成本t e,由于LWE體制的代理重加密運算為矩陣運算,無法與多項式環上的運算統一比較,這里只選取PSNTRUReEncrypt方案[1]、NTRU-ABD-PRE方案[20]和文獻[21]的代理重加密方案進行對比分析,由表6可知,本文方案較PS-NTRUReEncrypt和NTRU-ABD-PRE方案,提升了重加密的效率,減小了重加密操作中隨機多項式采樣帶來的時間成本. 表6 時間成本對比Table 6 Time cost comparison 本文總結了NTRU公鑰加密目前的研究成果并改進BI-NTRU-LPR方案,在保證方案IND-CPA安全性的同時減小了密鑰尺寸.基于改進的新型可證明安全NTRU變體,構造了一個可證明安全的單向抗合謀代理重加密方案,進一步完善了NTRU代理密碼體制.與目前已有的LWE型代理重加密方案相比,具有密鑰尺寸小、計算復雜度低、實用性強的優勢.但在實際應用場景下需要進一步完善NTRU代理重加密方案的功能特性,以實現對被授權者的細粒度訪問控制和對半可信代理者的代理轉換能力的條件及門限控制.
3.2 NTRU型代理重加密方案
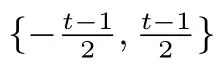
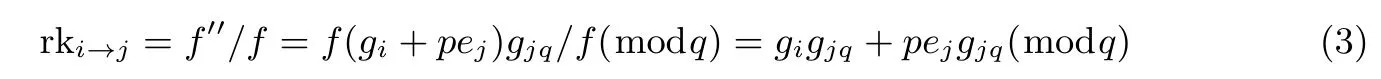
4 安全性分析
4.1 正確性分析
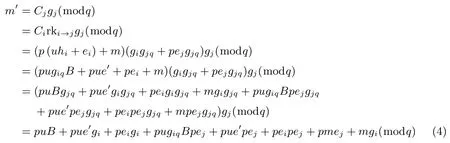
4.2 單向性
4.3 多跳性
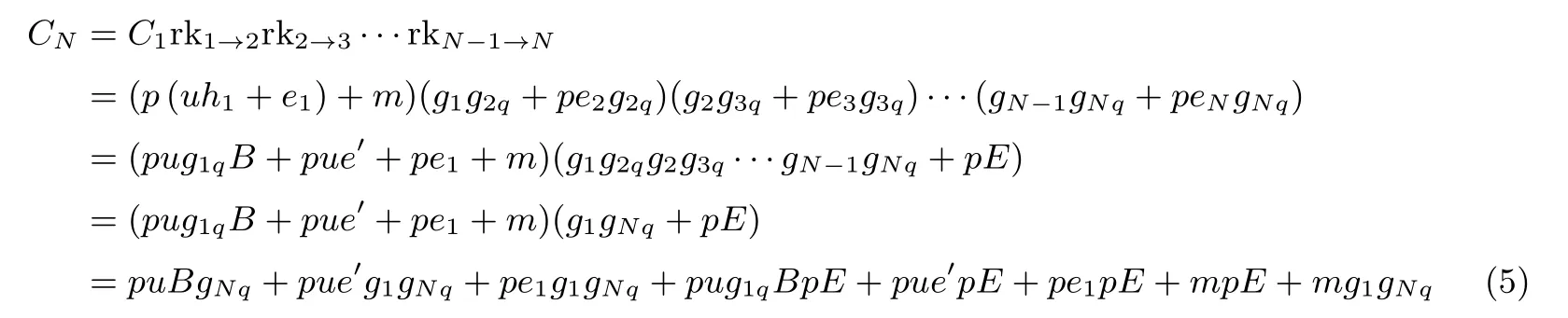
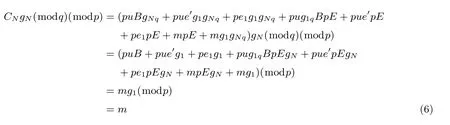
4.4 抗合謀性
4.5 安全性證明

5 效率分析
5.1 NTRU-LPR方案對比分析


5.2 NTRU-LPR-ReEncrypt方案對比分析



6 結束語

