三元Hf-C-N 體系的空位有序結構及其力學性質和電子性質的第一性原理研究*

彭軍輝 Tikhonov Evgenii

1) (西北工業大學材料學院,材料發現國際中心,西安 710072)

2) (太原工業學院材料工程系,太原 030008)

采用第一性原理方法,研究了三元Hf-C-N 體系的空位有序結構及其力學性質和電子性質.首先采用第一性原理和進化算法,預測得到8 種可能存在的熱力學穩定的Hf-C-N 空位有序結構;這些結構都具有巖鹽結構,與實驗發現的無序固溶體的結構類型一致.本文的預測結果證明了Hf-C-N 空位化合物能夠以有序結構形式存在,空位與C,N 原子都位于[Hf6]八面體間隙,這一結構特點與HfCx 的相同.然后采用第一性原理方法,計算了Hf-C-N 空位有序結構的力學性質,發現除C∶N=1∶4 外,相同C/N 下,隨著空位濃度的增大,Hf-C-N的體模量、剪切模量、彈性模量、Pugh 比、維氏硬度等降低;而Hf6CN4 (空位濃度為1/6)的維氏硬度高于Hf5CN4 (無空位),表現出空位硬化現象.最后,計算了Hf-C-N 空位有序結構的態密度和晶體軌道哈密頓分布,發現其具有強共價性和金屬性;且隨著空位濃度增大,總體鍵強減弱,因而模量減小.

1 引言

碳化鉿和氮化鉿作為典型的超高溫陶瓷材料,具有非常優良的綜合性能,如非常高的熔點、高強度、高硬度、良好的導電導熱性和化學穩定性等,因而可用于飛行器鼻錐、機翼前緣、熱結構防護、發動機熱端和推進系統等的關鍵部位或部件[1-4].另外,由于優異的抗腐蝕性、黏附性和高硬度等,氮化鉿可用作刀具防護的耐磨涂層[5].為了提高過渡金屬碳、氮化合物的性質,以滿足對材料性能越來越高的要求,研究者們常制備碳/氮化合物的超晶格結構[6,7]和納米尺度復合材料[8,9]等,以及采用空位強化[10-13]和合金化[14-19]等方法.

常溫常壓下,HfC 和HfN 均為B1 型巖鹽結構,鉿原子形成面心立方結構,碳、氮原子處于[Hf6]八面體間隙.HfC 和HfN 可形成三元無限固溶體,且實驗和理論上發現三元Hf-C-N 體系具有更好的力學性質[14-19].例如,Holleck[14]研究了HfC1—xNx的微觀硬度與組分之間的關系,發現HfN 的含量x=N/(C+N)=0.4 時,微觀硬度最大.Yang 等[15]研究得到x=0.2—0.6 時,HfC1—xNx的剪切模量、彈性模量、體模量最大,而納米硬度和顯微硬度隨著HfN 含量的增大而減小.理論上,Jhi 等[16]采用第一性原理方法,研究得到x=0.4 時,HfC1—xNx的剪切模量最大.Feng 等[17]和Balasubramanian等[18]采用第一性原理方法,計算了HfC1—xNx的力學性能和電子性質隨組分變化的關系,發現x=0.25 時,HfCxN1—x的彈性模量和硬度最大.Peng和Tikhonov[19]采用第一性原理和進化算法,研究了HfC1—xNx的結構、力學性質等隨組分的變化,發現x=0.25—0.3 時,HfC1—xNx的剪切模量、彈性模量、維氏硬度等最大,斷裂韌性也得到了改善.因此,相比于二元化合物,三元Hf-C-N 體系的模量、硬度和韌性等都提高了;合金化是改善力學性能的一種有效方法.

實際上,二元及以上過渡金屬碳/氮和碳氮化合物都存在一定濃度的空位,被稱為強非化學計量比化合物.Gusev 等[20]發現在一定條件下,空位會重新分布,晶體結構發生改變,即形成了空位有序結構.強非化學計量比化合物的性質將受到空位濃度及其分布(有序無序性)等影響[11,14,20-23].Rudy[22]研究發現Hf-C 體系中,HfC0.94的熔點最高.Holleck[14]研究發現隨著空位濃度的減小,TaNx,TaCx,NbNx和NbCx的微觀硬度先增加后減小;而TiCx,ZrCx,HfCx,TiNx和ZrNx的微觀硬度隨著空位濃度的減小而增大.Jhi 等[11]采用第一性原理方法,分別研究了Ti-N 和Nb-C 體系的剪切性質和電子性質,發現空位對Ti-N 和Nb-C 體系的力學性質產生了完全不同的影響,即空位硬化和軟化,且與Holleck[14]的實驗結果一致.Gusev 等[20]在著作中總結了二元強非化學計量比化合物的有序結構,并分析了空位有序性對性質的影響.

近年來研究人員采用第一性原理結合晶體結構預測等方法,對二元過渡金屬碳/氮化合物的有序結構進行了大量研究[24-38].基于第一性原理和進化算法,Yu 等[24-26]和Xie 等[27,28]分別采用晶體結構預測軟件USPEX[39-41],對過渡金屬碳化物(TM=Ti,Zr,Hf,V,Nb,Ta 等)的結構進行了預測,發現了一系列含陰離子空位的結構,包括TM2C,TM3C2,TM4C3,TM5C4,TM6C5,TM7C6和TM8C7等,并研究了空位對結構和力學性質的影響.Zhang 等[29]和Gunda 等[30]分別采用CE 方法[31]預測了ZrCx和TiCx的結構,Weinberger 和Thompson[32]基于有序參數函數方法[33]預測了第IVB,VB 族過渡金屬碳化物的穩定結構.基于第一性原理和進化算法,Yu 等[34,35]和Fan 等[36]分別預測了TiNx,ZrNx和HfNx的結構,除了含陰離子空位的化合物外,還發現含過渡金屬空位的結構如Zr15N16,Zr7N8,Zr4N5,Hf4N5和Hf5N6等,并研究空位對力學性質等的影響.采用USPEX[39-41],Zhao 等[37]和Li 等[38]分別預測了Nb-N 和Ta-N體系的穩定結構.

然而,目前關于三元過渡金屬碳/氮化合物空位有序結構及性質的報道還很少.Rudy[42]采用X 射線粉末圖譜法研究了Ta2VC2的結構,空間群為R3m,然而XRD 無法判斷碳原子和碳原子空位的具體分布情況.Erniraliev 等[43]在TixV1—xC0.5(0.2 ＜x＜ 0.3)固溶體中,發現了一種anti-CaCl2型的有序結構.Karimov 等[44]和Em 等[45]采用中子衍射方法研究了MCxNy(M=Ti,Zr)體系,發現空位濃度較小時,不存在有序結構;x+y＜ 0.74時,發現有序結構Fd3m.Em 和Tashmetov[46]采用中子衍射方法,發現TiCxNy(x+y≈ 0.63)中存在兩種有序結構-立方晶系(空間群為Fd3m)和三方晶系(空間群為R3m或P3121).Rudy[22]研究了高溫下Hf-Ta-C 體系的結構和性質,發現許多含空位的三元化合物,均為具有巖鹽結構或Ta2C型的無序固溶體,但沒有發現有序結構.Binder等[47]研究了1423 K 時,Ti-C-N,Zr-C-N 和Hf-C-N體系的相平衡區間,Ti(CxN1—x)1—y,Zr(CxN1–x)1—y,Hf(CxN1—x)1—y均是B1 型無序結構.Yang 等[15]研究了Ti(CxN1—x)0.81的微觀硬度、納米硬度、體模量、剪切模量、彈性模量等,但沒有給出Ti(CxN1—x)0.81的結構類型.Hong 和van de Walle 等[48]采用從頭算分子動力學方法,模擬了含陰離子空位的Hf-C-N 和Hf-Ta-C 體系的熔點,使用的均是B1 型超胞結構.Buinevich 等[49]合成了非化學計量比化合物HfC0.5N0.35,為B1 型無序結構,并測得其熔點大于HfC0.98的,維氏硬度為21.3 GPa,斷裂韌性為4.7 MPa·m1/2.因而,實驗上要研究三元過渡金屬碳/氮化合物的有序結構非常困難,第一性原理結合晶體結構預測是一種有效方法.

綜上所述,三元過渡金屬碳氮化合物的性質除了受到化學組成的影響外,還將受到空位的濃度及其分布等的影響.為了研究三元Hf-C-N 體系,建立組分-結構-性質的關系,必須考慮空位對結構及性質的影響.然而,目前實驗和理論上,很少關于三元Hf-C-N 空位有序結構、力學性質及其關系的研究報道.本文基于第一性原理和進化算法,采用晶體結構預測軟件USPEX[39-41]—已成功應用于二元過渡金屬碳/氮化合物及許多新結構的預測[24-28,34-41],搜索了三元Hf-C-N 的空位有序結構,研究了空位、化學組成等對力學性質的影響.為該材料的實驗合成、制備和應用等提供了理論指導和依據,也為其他三元過渡金屬碳氮化合物的研究提供了借鑒.

2 計算方法

晶體結構預測軟件USPEX[39-41]預測材料結構時,模仿生物進化機制,基于進化算法,采用隨機生成、遺傳、變異等操作產生結構;然后,基于能量、硬度或體積等,搜索得到滿足目標函數(如能量最低)的晶體結構.USPEX[39-41]可以直接從材料的化學元素組成出發,無需其他實驗數據,即可預測得到其結構.根據無偏差測試[50],USPEX[39-41]在計算效率和可靠性上都優于其他晶體結構預測方法.

采用USPEX[39-41]分別搜索了Hf6C4N,Hf6C3N,Hf6C3N2,Hf4C2N,Hf3CN,Hf5C2N2,Hf4CN2,Hf6C2N3,HfCN3和Hf6CN4等組分的結構,單胞中原子數分別為22,20,22,14,10/20,22,14,22,20 和22.初始結構(共60 個)由USPEX[39-41]隨機產生,從第2 代開始,每代結構(共50 個)分別由遺傳(40%)、軟模變異(20%)、晶格變異(10%)、原子位置交換(10%)、隨機(20%)等進化操作產生.對USPEX[39-41]產生的每個結構,采用VASP軟件[51]計算其能量,篩選出能量最低的結構.當連續20 代能量最低的結構相同,或搜索了30 代結構時,計算停止.

然后,采用VASP 軟件[51]對Hf-C-N 各組分能量最低結構進一步進行結構優化和性質計算.結構優化時,離子實與價電子之間的相互作用,采用投影綴加波方法[52]進行描述,截斷能為600 eV,電子與電子間交換關聯能采用GGA-PBE[53]方法進行處理.布里淵區高對稱點間距為2π × 0.018 ?—1.能量收斂判據為:能量差為10—8eV/atom,壓力差為10—3eV/?.基于“凸包結構”判斷得到熱力學穩定結構,即某一結構分解為任意其他結構時,分解能為正,則該結構為熱力學穩定結構.然后,采用VASP 軟件[51]計算彈性常數,根據經驗公式[54-58]計算得到體模量、剪切模量、彈性模量、泊松比、維氏硬度、Pugh 比等.最后,基于密度泛函微擾理論,采用Phonopy 軟件[59]計算Hf-C-N 空位有序結構的聲子譜曲線,判斷晶格動力學穩定性.采用VESTA 軟件[60]畫出其晶體結構和模擬X 射線衍射圖譜.采用LOBSTER 軟件[61]計算Hf-C-N 空位有序結構的晶體軌道哈密頓分布(—COHP).

3 結果與討論

3.1 晶體結構預測及Hf-C-N 空位有序結構

由于Hf-C-N 體系的性質受到空位濃度的影響,首先采用空位調控的方法,對三元Hf-C-N體系的組分進行設計,采用晶體結構預測軟件USPEX[39-41]結合VASP[51],搜索了三元空位有序結構.圖1(a)為三元Hf-HfC-HfN 體系的能量凸包圖,反應焓ΔH(eV/atom)的計算公式如下:

李波：紅土地的景區萎縮。原因主要有三方面：一個是退耕還林還草，一大部分地區消失了；第二個原因是土地撂荒；第三個原因是亂挖亂建。2010年左右這種變化開始明顯，到2015年左右，紅土地的攝影旅游到了一個鼎盛期，之后就慢慢衰退了。

圖1(a) 常壓下,三元Hf-HfC-HfN 體系的能量凸包圖,黑色球表示熱力學穩定結構,其他為亞穩結構;(b) Hf-C-N 空位有序結構的X 射線衍射模擬圖譜,衍射源為Cu Kα 射線Fig.1.(a) Enthalpy convex-hull of ternary Hf-HfC-HfN system at ambient pressure.The black sphere indicates stable structure,and others are metastable structure.(b) The simulated X-ray diffractions of Hf-C-N vacancy ordered structures with a copper Kα X-ray source.

根據“凸包結構”判據,如圖1(a)所示,除文獻[19]中報道的不含空位的HfC1—xNx外,本文還預測得到了8 種可能存在的熱力學穩定的空位有序結構,其化學式、反應焓ΔH(eV/atom)和空位濃度等,如表1 所列.就我們所知,目前還沒有關于三元Hf-C-N 空位有序結構的報道,本文預測得到的這些穩定結構都是第一次被發現的.且本文預測得到了Hf-C-N 空位有序結構的晶體學數據,如空間群、晶格常數等,如表1 所列.

圖1(b)為Hf-C-N 空位有序結構的X 射線衍射模擬圖譜,三元化合物的衍射峰形狀與HfC,HfN 的相同,且衍射角位于HfC,HfN 的衍射角之間;即結構與HfC 和HfN 的結構相同,都具有巖鹽結構.此結果與Binder 等[47]和Buinevich 等[49]發現的Hf-C-N 無序固溶體的結構類型一致.本文的理論預測結果證明了Hf-C-N 空位化合物能夠以有序結構的形式存在.

圖2 為Hf-C-N 空位有序結構某一晶面上的空位分布,黑色方框表示空位,取代的是部分C 和N 原子的位置;即對于Hf-C-N 化合物,原子數比Hf/(C+N)小于化學計量比1∶1 時,空位占據剩余C 和N 原子的晶格位置.則C 和N 原子的配位數均為6,而Hf 的配位數小于6,Hf 原子的配位數如表1 所列.與二元HfCx等[24-28]的結構相似,過渡金屬原子形成[Hf6]八面體,八面體共棱連接,C,N 原子和空位都處于八面體間隙位置.圖3 為Hf-C-N 空位有序結構的聲子譜曲線,在布里淵區(高對稱點路徑采用SeeK-path 軟件[62]得到),都不存在虛頻,證明這些結構都是晶格動力學穩定的.

圖2 Hf-C-N 空位有序結構在某一晶面上的空位分布 (a) Hf6C4N-C2/m (0 0 1);(b) Hf6C3N-C2(1 0 0);(c) Hf6C3N2-C2/m(1 0 0);(d) Hf3CN-C2(1 0 0);(e) Hf6C2N3-C2(1 0 0);(f) Hf4CN2-Cmmm (0 0 1);(g) Hf6CN3-C2/m (1 0 0);(h) Hf6CN4-C2/m(0 0 1)Fig.2.Vacancies on the crystallographic plane:(a) Hf6C4N-C2/m (0 0 1);(b) Hf6C3N-C2(1 0 0);(c) Hf6C3N2-C2/m (1 0 0);(d) Hf3CN-C2(1 0 0);(e) Hf6C2N3-C2(1 0 0);(f) Hf4CN2-Cmmm (0 0 1);(g) Hf6CN3-C2/m (1 0 0);(h) Hf6CN4-C2/m (0 0 1).

圖3 Hf-C-N 空位有序結構的聲子譜曲線 (a) Hf6C4N-C2/m;(b) Hf6C3N-C2;(c) Hf6C3N2-C2/m;(d) Hf3CN-C2 ;(e) Hf6C2N3-C2;(f) Hf4CN2-Cmmm;(g) Hf6CN3-C2/m;(h) Hf6CN4-C2/mFig.3.Phonon dispersion curves of (a) Hf6C4N-C2/m,(b) Hf6C3N-C2 ,(c) Hf6C3N2-C2/m,(d) Hf3CN-C2 ,(e) Hf6C2N3-C2,(f) Hf4CN2-Cmmm,(g) Hf6CN3-C2/m,(h) Hf6CN4-C2/m.They are all dynamical stable because no imaginary frequencies were found in Brillouin zone.

表1 Hf-C-N 空位有序結構的空間群、晶格常數、反應焓ΔH (eV/atom)、Hf 原子的配位數(CN) 和空位濃度(CV)Table 1.Space group,lattice constants,the enthalpy of reaction ΔH (eV/atom),coordination number (CN) of Hf and the concentration of vacancy (CV) of Hf-C-N vacancy ordered structures.

3.2 Hf-C-N 空位有序結構的力學性質

首先采用VASP 軟件[51]計算了Hf-C-N 空位有序結構的彈性常數,如表2 所列,這些結構的彈性常數都滿足Born 判據[63],即都是力學穩定的.再根據計算的彈性常數,基于Voigt-Reuss-Hill 近似[54-56],得到體模量B、剪切模量G、彈性模量E、泊松比等.采用Chen-Niu 模型[57],計算Hf-C-N空位有序結構的維氏硬度HV,計算公式如下:

表2 Hf-C-N 空位有序結構的彈性常數Cij (單位:GPa)Table 2.Calculated elastic constants Cij (in GPa) of Hf-C-N vacancy ordered structures.

其中Pugh 比[58]k=G/B.

Hf-C-N 空位有序結構的力學性質如表3 所列,可以看到這些結構都具有非常高的體模量、剪切模量、彈性模量和維氏硬度等.為了對比,HfC1—xNx的力學性質也在表3 中列出,盡管這些結構的力學性質已經在文獻[19]中被報道了.

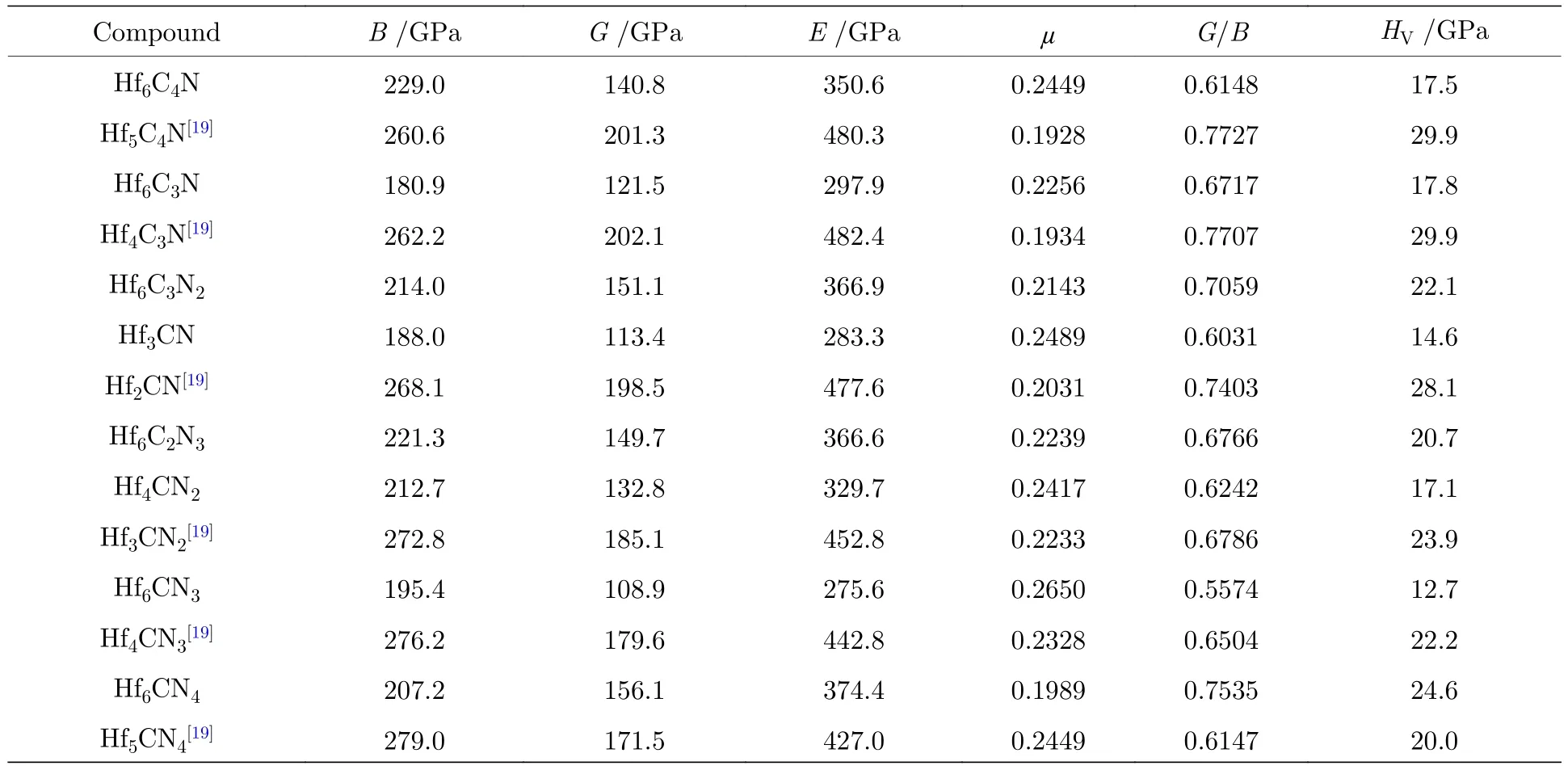
表3 Hf-C-N 空位有序結構和HfC1—xNx[19]的力學性質—體模量(B)、剪切模量(G)、彈性模量(E)、泊松比(μ)、Pugh 比(G/B)、維氏硬度(HV)等Table 3.Mechanical properties—bulk modulus (B),shear modulus (G),elastic modulus (E),Poisson’s ratio (μ),Pugh’s ratio (G/B),Vickers hardness (HV) of Hf-C-N vacancy ordered structures and HfC1—xNx[19].

圖4 為三元Hf-HfC-HfN 體系的力學性質-組分相圖,其中包括三元空位有序結構,Hf-C,Hf-N 體系和HfC1—xNx等的性質[19,25,36].從圖4 可以看到:相同C/N 比下,隨著空位濃度的增大,體模量、剪切模量、彈性模量等減小;如圖5 和圖6 所示,空位濃度增大,Hf-C-N 化合物的有效價電子濃度及總體鍵強減弱,材料抵抗外力的能力減小,則Hf-C-N 化合物的模量減小.然而,Hf6CN4(空位濃度為1/6)的維氏硬度和Pugh 比大于Hf5CN4(無空位)的維氏硬度和Pugh 比,表現出空位硬化現象;而其他組分下,C/N 比相同時,維氏硬度和Pugh 比等隨空位濃度的增大而減小.如圖4(f)所示,泊松比的變化規律與Pugh 比的正好相反.

圖4 三元Hf-HfC-HfN 體系的力學性質-組分相圖 (a) 體模量(B);(b) 剪切模量(G);(c) 彈性模量(E);(d) 維氏硬度(HV);(e) Pugh 比(G/B);(f) 泊松比(μ)Fig.4.Mechanical properties-composition diagrams of ternary Hf-HfC-HfN system:(a) Bulk modulus (B);(b) shear modulus (G);(c) elastic modulus (E);(d) Vickers hardness (HV);(e) Pugh’s ratio (G/B);(f) Poisson’s ratio (μ).

3.3 Hf-C-N 空位有序結構的電子性質

為了分析Hf-C-N 空位有序結構的成鍵特性和空位對電子性質的影響,對其態密度、分態密度和晶體軌道哈密頓分布進行了計算.圖5(a)—(h)為Hf-C-N 空位有序結構的態密度和分態密度圖,在能級為—8 至—2 eV,Hf-d 軌道與C-p 和N-p軌道之間存在大量重疊,即存在強的雜化作用,則Hf—C 和Hf—N 鍵存在強的共價性.這是Hf-C-N空位有序結構具有非常高的模量和硬度的原因.同時,在Fermi 面上存在自由電子,證明其具有金屬性.這些成鍵特點和二元過渡金屬碳、氮化合物[24-28]及HfC1—xNx[19]的相同.對比Hf2CN (不含空位,該結構及其電子性質已在文獻[19]中報道)和Hf3CN(空位濃度為1/3)的總態密度,分析空位對態密度的影響,如圖5(i)所示:可以看到兩者價電子的能級排布基本不變,然而Hf3CN 各能級處對應的價電子狀態數小于Hf2CN 的;這是由于空位存在,Hf3CN 的有效價電子濃度(VEC 為7)小于Hf2CN的(VEC 為8.5).而空位對其他Hf-C-N 空位有序結構的態密度也存在相似的影響.

圖5(a) Hf6C4N-C2/m,(b) Hf6C3N-C2,(c) Hf6C3N2-C2/m,(d) Hf3CN-C2,(e) Hf6C2N3-C2,(f) Hf4CN2-Cmmm,(g) Hf6CN3-C2/m 和(h) Hf6CN4-C2/m 的態密度和分態密度;(i) Hf3CN 和Hf2CN 的總態密度對比;其中Fermi 能級位于0 eVFig.5.Density of state (DOS) and partial density of state (PDOS) normalized by per HfCxNy of (a) Hf6C4N-C2/m,(b) Hf6C3N-C2,(c) Hf6C3N2-C2/m,(d) Hf3CN-C2,(e) Hf6C2N3-C2 ,(f) Hf4CN2-Cmmm,(g) Hf6CN3-C2/m and (h) Hf6CN4-C2/m;(i) the total DOS of Hf3CN and Hf2CN normalized by per HfCxNy.The Fermi level is at 0 eV.

圖6 為Hf-C-N 空位有序結構的晶體軌道哈密頓分布(—COHP),同時對比了HfC1—xNx的—COHP.圖6 中,正值表示成鍵態,負值表示反鍵態.從圖6 可以看到,Hf-C-N 空位有序結構與HfC1—xNx的—COHP 相似,雜化能級(—8 — —2 eV)范圍內,存在寬的成鍵區域,即具有強的共價性,與態密度的計算結果一致.—COHP 的積分用ICOHP 表示,ICOHP 反映了化學鍵的強弱.表4 為Hf-C-N 化合物的Hf—C,Hf—N 和Hf—Hf 鍵的—ICOHP 的大小,可以看到:相同C/N 比下,含空位化合物(如Hf3CN)的Hf—C 鍵和Hf—N 鍵的鍵強要比不含空位的(如Hf2CN)更強,且Hf—Hf 金屬鍵也更強.然而,隨著空位濃度增大,Hf—C 鍵和Hf—N 鍵的總鍵數目減小(如表1 所列Hf 的配位數小于6),則總體鍵強減弱,因此抵抗外力的能力減弱,Hf-C-N化合物的體模量、剪切模量和彈性模量隨之減小.

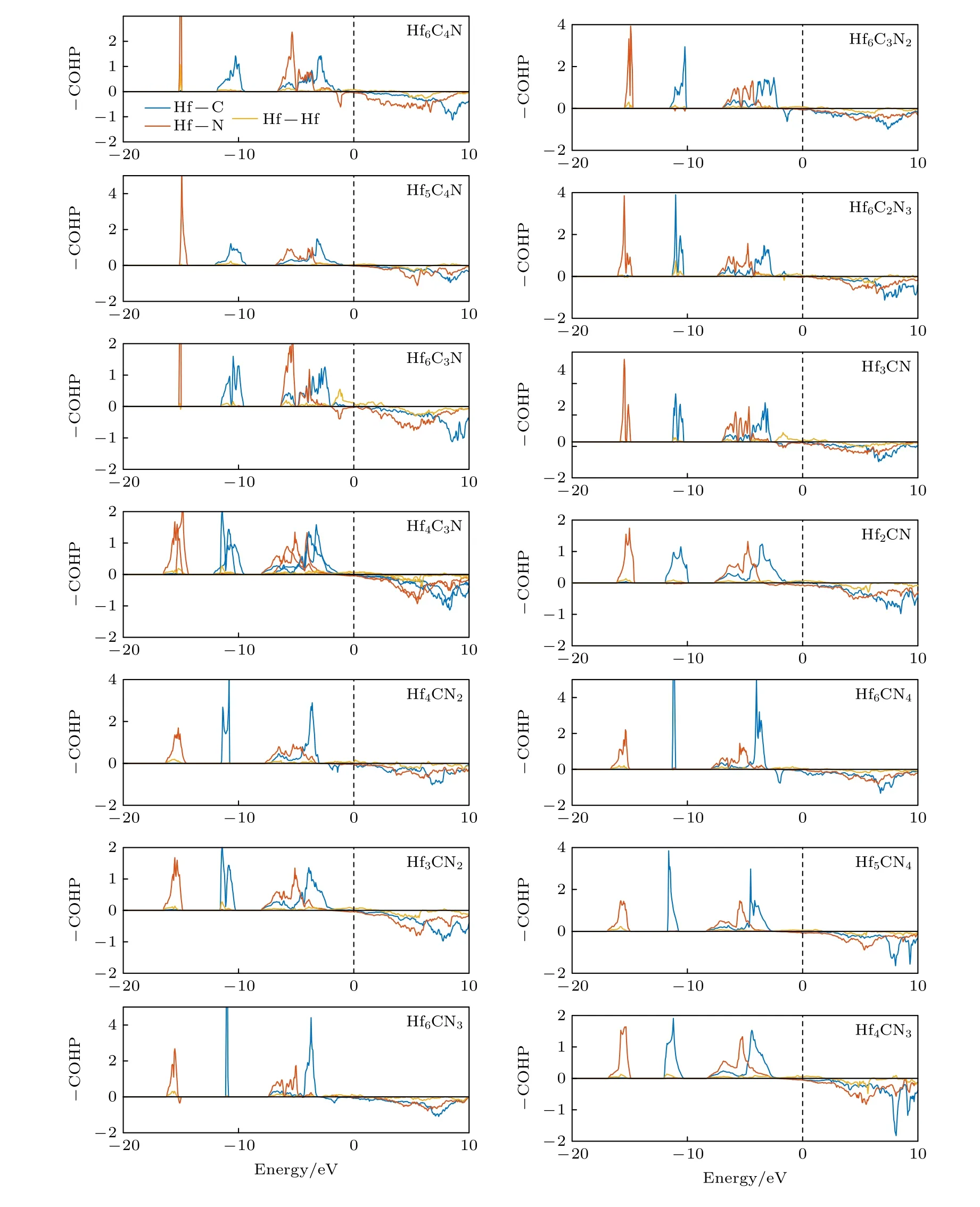
圖6 Hf-C-N 化合物的晶體軌道哈密頓分布(—COHP),Fermi 能級位于0 eVFig.6.Crystal orbital Hamilton populations (—COHP) of Hf-C-N compounds.The Fermi level is at 0 eV.

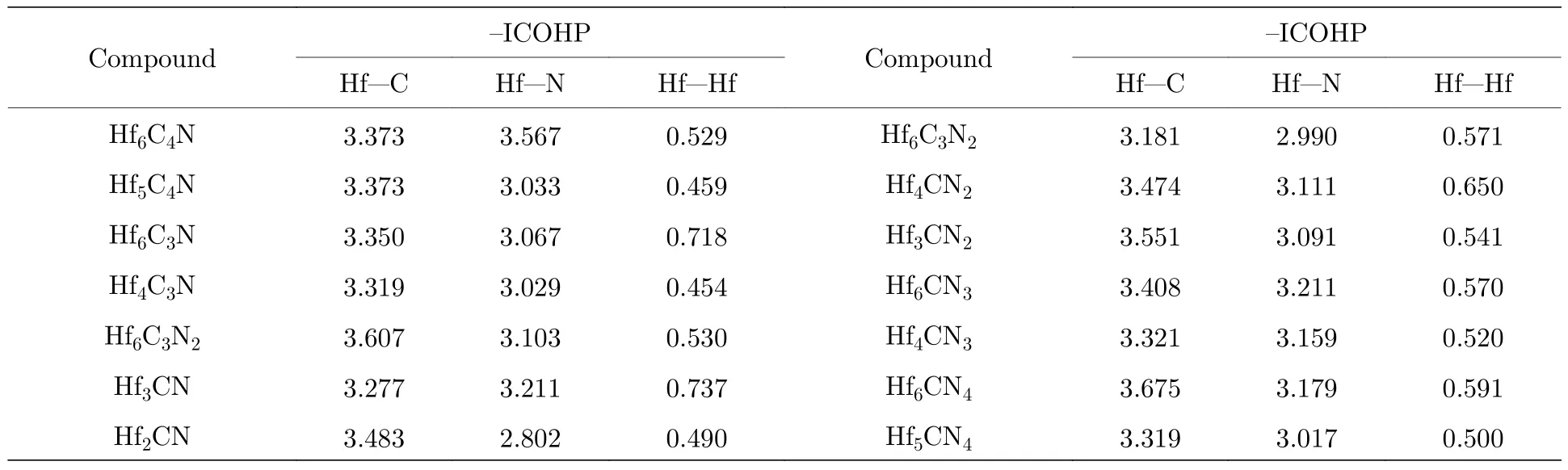
表4 Hf-C-N 化合物的晶體軌道哈密頓分布的積分值(—ICOHP)Table 4.Integrated crystal orbital Hamilton populations (—ICOHP) of Hf-C-N compounds.

4 結論

本文采用空位調控方法,對三元Hf-C-N 體系的組分進行了設計;采用第一性原理方法,研究了Hf-C-N 的空位有序結構及其力學性質和電子性質:

1) 搜索發現了8 種新的Hf-C-N 空位有序結構,且都具有巖鹽結構;空位有序地分布在[Hf6]八面體間隙,證明了Hf-C-N 空位化合物可以以有序結構的形式穩定存在;

2) Hf-C-N 空位有序結構具有非常高的模量和硬度;相同C/N 比時,隨著空位濃度的增大,體模量、剪切模量、彈性模量減小;

3) 發現了一個空位硬化現象,Hf6CN4(空位濃度為1/6)的硬度大于Hf5CN4(無空位)的硬度;

4) Hf-C-N 空位有序結構的化學鍵具有強共價性和金屬性.隨著空位濃度的增加,Hf—C 和Hf—N共價鍵鍵強增大,金屬性增強,但總體鍵強減弱,使其模量減小.