混合量子-經典算法:基礎、設計與應用

陳然一鎏 趙犇池 宋旨欣 趙炫強 王琨 王鑫

(百度研究院量子計算研究所,北京 100193)

量子計算作為一種新興的計算范式,有望解決在組合優化、量子化學、信息安全、人工智能領域中經典計算機難以解決的技術難題.目前量子計算硬件與軟件都在持續高速發展,不過未來幾年預計仍無法達到通用量子計算的標準.因此短期內如何利用量子硬件解決實際問題成為了當前量子計算領域的一個研究熱點,探索近期量子硬件的應用對理解量子硬件的能力與推進量子計算的實用化進程有著重要意義.針對近期量子硬件,混合量子-經典算法(也稱變分量子算法)是一個較為合理的模型.混合量子-經典算法借助經典計算機盡可能發揮量子設備的計算能力,結合量子計算與機器學習技術,有望實現量子計算的首批實際應用,在近期量子計算設備的算法研究中具有重要地位.本文綜述了混合量子-經典算法的設計框架以及在量子信息、組合優化、量子機器學習、量子糾錯等領域的研究進展,并對混合量子-經典算法的挑戰以及未來研究方向進行了展望.

1 引言

量子計算是基于量子力學與計算機科學的一門新興學科,被認為在人工智能、信息安全、生物制藥、量子化學等領域能帶來極具潛力的應用.特別地,通用量子計算機理論上可以高效地解決經典計算機無法高效解決的大數分解[1]、數據搜索[2]、量子模擬[3]等問題.隨著學術界與工業界對量子計算技術研發力度的逐步加大,量子計算硬件的技術在不斷地進步[4-7].盡管如此,目前的技術離通用量子計算機要求的保真度、相干時間等條件還有一段距離.因此,從目前已實現幾十量子位到未來實現通用量子計算這段時間,如何利用好當前不斷增強的有噪中規量子(noisy intermediate-scale quantum,NISQ)計算設備[8],是一個至關重要的問題,也是當前量子計算領域的一個研究熱點.

NISQ 計算設備有從幾十到幾百的量子位,這些量子位是沒有糾錯的物理量子比特(而非邏輯量子比特),只能進行相干時間有限的不完美的量子操作.在追尋量子計算優勢的過程中,學者們基于NISQ 計算設備進行了諸多應用的探索,涵蓋了組合優化[9]、量子化學[10]、量子物理[8]、機器學習[11,12]等諸多方向,目標是盡可能利用NISQ 設備的能力去完成特定的對于經典計算相對有挑戰的任務.

基于NISQ 設備,最常見的算法模型為混合量子-經典算法,旨在借助經典計算機的力量盡可能發揮NISQ 計算設備的能力去解決具體的問題.混合量子-經典算法的一部分任務由量子計算設備完成,然后通過經典計算調整量子計算部分的可調參數,反復迭代最后輸出結果.由于采用的電路擬設可以由NISQ 設備高效實現,混合量子-經典算法被認為可以基于近期設備發揮量子優勢.混合量子-經典算法在諸多領域有著廣泛應用,其中最具有代表性的包括求解組合優化問題的量子近似優化算法(quantum approximate optimization algorithm,QAOA)[13]與求解基態能量問題的變分量子本征求解器(variational quantum eigensolver,VQE)[10,14].囿于目前對外開放的量子設備有限,同時又涉及經典與量子設備之間的交互,目前此類混合算法通常在模擬平臺[15-17]上進行小規模開發,然后通過硬件平臺驗證效果.量槳[15]是國內較為完善的混合算法開發平臺,借助技術領先的產業級深度學習框架飛槳[18,19],通過深度學習賦能量子計算領域的前沿研發.

本綜述就混合量子-經典算法的概念、原理、應用實例、挑戰與瓶頸等方面進行詳細的介紹.具體的文章結構如下:第2 節介紹混合量子-經典算法中的基本概念與設計思想;第3 節列舉混合量子-經典算法在不同領域中具有代表性的若干應用;第4 節討論混合量子-經典算法目前面臨的主要挑戰;第5 節進行總結.

本文常用的符號如表1 所列.

表1 主要符號表Table 1.Notations.

2 基本概念

混合量子-經典算法的核心在于將計算任務轉化為優化問題.以最具代表性的變分量子本征求解器(VQE)[10]為例,VQE 將求解哈密頓量H的基態能量E0問題轉化為整個密度算符(量子態)集合上的優化問題:

其中D表示所有與H維數相同的密度算符的集合,而 Tr[Hρ] 可以通過對量子態的測量得到.進一步地,如果將量子態ρ視作從某個固定量子態ρin出發,經過一個參數化酉變U(θ) 演化之后的量子態ρ=U(θ)ρinU(θ)?,則VQE 可以表示為一個參數空間上的優化問題:

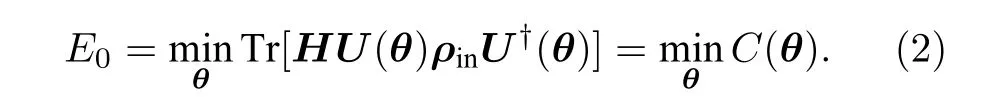
通過調整參數θ以最小化C(θ),VQE 最終得到目標基態能量E0.

從VQE 的例子中可以看出,混合量子-經典算法通常包含一個精心設計的損失函數C,使得當C取最小(或最大)值時可以實現計算任務.隨后,混合量子-經典算法通過調整一個參數化酉變U(θ)最小(或最大)化損失函數,從而實現計算任務.值得注意的是,由于損失函數實現了從實數(可調參數)到實數(測量結果)的映射,混合量子-經典算法可以使用經典優化方法來優化可調參數θ.可見,算法結合了量子設備的計算能力與經典設備的優化方法,故得名混合量子-經典算法.典型的混合量子-經典算法流程如圖1 所示.

由圖1 可知,實現一個混合量子-經典算法必須考慮如何設計損失函數將計算任務轉化為優化問題,以及如何構造一個參數化酉變(如果算法處理的任務涉及到經典數據,則需要額外的編碼過程將數據轉換成量子數據.詳見3.4.1 節).此外,混合量子-經典算法中采用的經典優化方法往往會對算法的效率和準確度產生影響.特別地,相比于不基于梯度的優化方法,解析梯度以及解析高階導數因為需要運行更少的量子電路來決定優化方向成為混合量子-經典算法所關注的重點.本節接下來將就這幾個混合量子-經典算法中的基本概念展開討論.

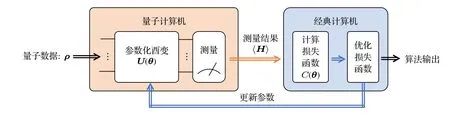
圖1 混合量子-經典算法流程Fig.1.Diagram for hybrid quantum-classical algorithms.

2.1 損失函數

損失函數是混合量子-經典算法設計的核心.一般來說,為保證函數值可以在量子設備上通過測量高效計算,混合量子-經典算法中的損失函數具有如下形式:

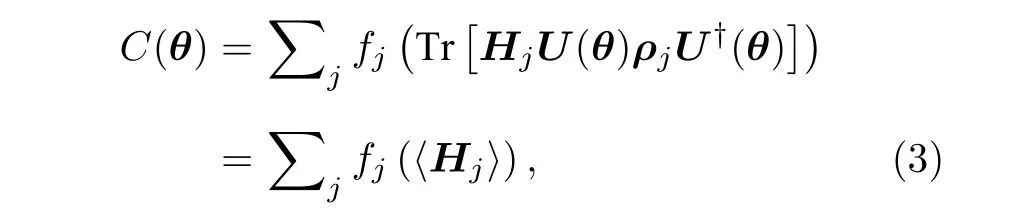
其中ρj是一組輸入量子態,Hj是一組厄米特算符,表示在電路末端進行Hj測量的結果,fj是一組經典函數,表示對測量結果的經典后處理.由混合量子-經典算法的框架可知,損失函數的設計必須滿足:當且僅當損失函數達到全局最小時,計算任務求得解.這被稱為混合量子-經典算法的忠實性條件[20].對于VQE 算法,由于其損失函數直接設為哈密頓量的測量值,忠實性條件自然滿足.

需要指出的是,考慮到在近期設備上的適用性,混合量子-經典算法的損失函數必須能夠高效地計算.根據厄米特算符Hj的種類,計算損失函數的方法可大致分為以下幾種:

1)Hj是泡利算符.此時損失函數可以直接通過對量子態的泡利測量得到.特別地,在許多常見的物理模型(如伊辛模型)中,Hj寫成局部泡利算符的線性組合:

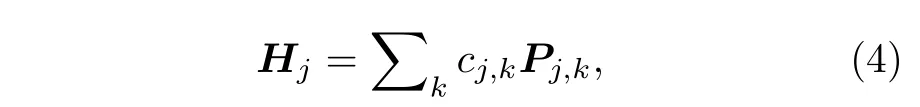
其中Pj,k是泡利算符,且只不平凡地作用在局部的量子比特上.若每一個Pj,k最多只作用于m個量子比特,則稱損失函數為m-局部的.局部損失函數相較于全局損失函數在梯度消失問題上被認為更具有優勢[21](詳見4.3 節).

2)Hj是密度算符σ.此時計算任務往往包含計算量子態之間的態重疊(Tr[ρσ]),或量子態的純性(Tr[ρ2]).這類的損失函數可通過交換測試[22]或其變種破壞性交換測試[23]在量子設備上計算(電路實現分別如圖2(a)和圖2(b)所示).同時,由于密度算符之間的Frobenius 距離可以寫成如下形式:

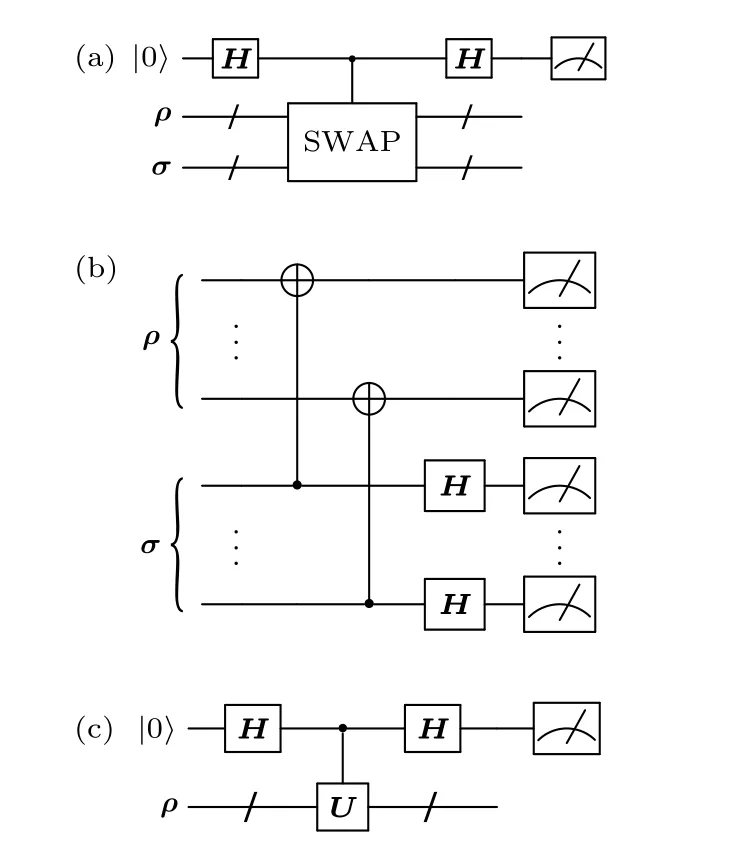
圖2(a) 交換測試電路;(b)破壞性交換測試電路;(c) 哈達瑪測試電路Fig.2.(a) Swap test circuit;(b) destructive swap test circuit;(c) Hadamard test circuit.

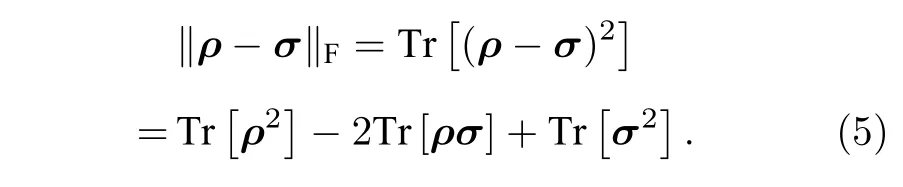
故密度算符的Frobenius 距離也可以由交換測試得到,其常見于量子態制備相關的任務.

3)Hj中包含酉算符.由于酉算符自身不是厄米特算符,此時需要對酉算符進行變換,常見的變換包括哈達瑪測試[24],用于計算

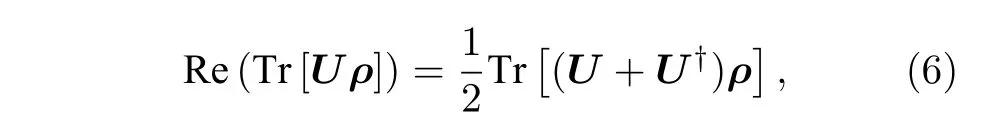
哈達瑪測試的電路實現如圖2(c)所示.同時,通過將哈達瑪測試電路輸入端的|0〉替換為-i|1〉)即可計算 Im(Tr[Uρ]) .

2.2 參數化酉變

作為典型的NISQ 算法,混合量子-經典算法實現的關鍵在于采用近期設備可實現的參數化酉變.參數化量子電路(parameterized quantum circuit,PQC)是一種通用的參數化酉變實現方式.在PQC 中,電路一般采用分層結構:

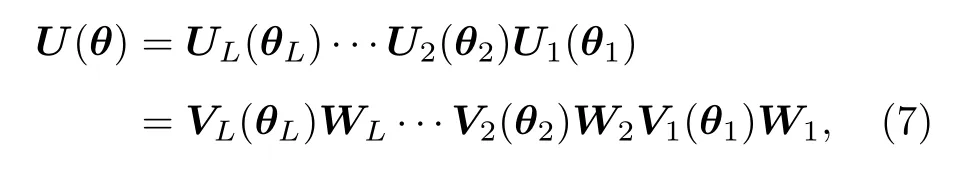
式中L被稱為電路的層數.由于設備噪聲的存在,近期設備所能提供的有效的電路寬度(量子比特數n)和深度(層數L)將受到限制.同時,為使電路能夠在近期設備上高效實現,在電路的每一層Ul(θl)=Vl(θl)Wl中,參數化的酉門Vl(θl)=Πke-iθkAk/2一般采用單比特旋轉門或含參雙比特門(ZZ 門);而不含參的酉門Wl作為連接層,一般由臨近量子比特間的CNOT 或CZ 兩比特門構成,為電路提供糾纏能力.參數化電路的結構也常被稱為擬設.由于參數化量子電路的邏輯結構與設計思想和機器學習中的神經網絡相似,參數化量子電路又被稱為量子神經網絡(quantum neural network,QNN).

在針對特定問題的算法中,可以通過問題的解的先驗信息針對性地設計電路擬設(如組合優化問題中的量子交替算符擬設[9]等).而在針對一般問題的電路結構設計中,或當問題的解不存在先驗信息時,電路結構的每一層Ul(θl) 往往采用相同的結構,即Ul(θl)=U(θl)=V(θl)W.文獻[25]列舉了若干常見的硬件高效擬設.此外,文獻[21]設計了一種交錯分層擬設.這樣的擬設在寬度或深度增大時會面臨電路可訓練性變差等問題.相對地,一些每層結構各不相同的電路擬設在特定任務下擁有更好的表現.下面介紹幾種特殊的的電路擬設.

1) 量子感知機[26,27].類比于經典神經網絡中的感知機模型,在量子感知機模型中,每個神經元對應一個量子比特,神經元之間的連接對應作用在兩端的量子比特上的酉變.量子感知機模型及其對應的量子電路模型如圖3(a)所示.一種耗散量子感知機模型[27]在節省量子比特數方面具有一定優勢.

2) 量子卷積神經網絡(quantum convolutional neural network,QCNN)[28].在QCNN 中,電路各層被進一步分為卷積層和池化層.卷積層電路由參數化的酉門構成,而在池化層中,電路通過測量部分量子比特減小系統的維度.此外,一種樹張量網絡[29]也采用了類似的結構逐層減小系統的寬度.QCNN 和樹張量網絡的結構如圖3(b)所示.由于系統的有效寬度隨層數快速減小,QCNN 等技術有望避免梯度消失問題[30].

3) 影子電路[31].受到經典影子學習[32]的啟發,影子電路模型通過對多次局部酉變和局部測量結果的后處理學習目標特征.在每一次影子電路的運行中,參數化的酉門只作用在部分系統上,然后對這部分系統進行測量,這種部分系統的測量信息被稱為“影子”;最后,將所有的“影子”進行經典后處理(例如全連接的經典神經網絡)以提取特征.影子電路模型如圖3(c)所示.由于采用了局部的電路和測量,影子電路模型在節約計算資源(需要訓練的參數量)和可訓練性方面更有優勢.

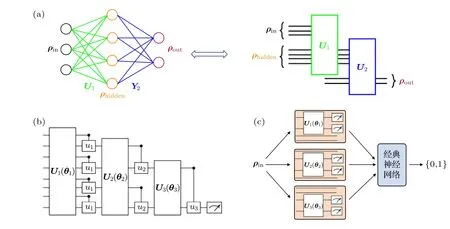
圖3 (a) 量子感知機;(b)量子卷積神經網絡;(c)影子電路Fig.3.(a) Quantum perceptron;(b) quantum convolutional neural network;(c) shadow circuit.

參數化量子電路的設計目前主要面臨兩個挑戰:其一是如何在有限的深度下保證擁有足夠的表達能力和糾纏能力來完成任務,其二是如何保證參數的可訓練性.第4 節將就這兩個問題作進一步討論.

2.3 優化方法

由于混合量子-經典算法將損失函數的優化任務“外包”給了經典計算機,絕大多數經典優化方法都可以用于混合量子-經典算法中的優化步驟.常用的混合量子-經典算法的經典優化方法中,基于梯度的方法有批量梯度下降、ADAM 優化、涉及多樣本的隨機梯度下降(stochastic gradient decent,SGD)、以及基于梯度估計的同步擾動隨機逼近算法(simultaneous perturbation stochastic approximation,SPSA)等.由于混合量子-經典算法中損失函數的解析梯度可以在量子設備上直接計算(詳見2.4 節),SGD 和ADAM 被廣泛應用于各類混合量子-經典算法,特別是算法的經典模擬[33]中;同時,非梯度的優化方法包括下山單純形法、粒子群算法、貝葉斯估計等,這些優化算法的詳細內容可參閱優化理論相關教材[34].

值得一提的是,基于參數化量子電路特有的屬性,專門針對混合量子-經典算法的優化方法也相繼被提出.一種基于梯度的優化方法被稱為量子自然梯度[35]優化.相比于傳統的梯度下降法,量子自然梯度優化在每輪迭代中參數更新時需額外計算因子g+:

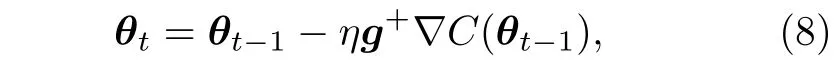
其中g為Fubini-Study 度量張量,g+表示g的偽逆.更進一步地,由于Fubini-Study 度量張量g的分塊對角矩陣近似也可以在量子設備上直接計算(詳見2.4 節),結合解析梯度?C,整個量子自然梯度優化的參數更新便可以在混合量子-經典算法的框架下實現.相比于傳統的梯度下降法,量子自然梯度在一些VQE 問題中具有更快的收斂速度.

另一類針對混合量子-經典算法的非梯度優化方法被稱為量子序列最小優化[36-38].此類優化方法的關鍵在于利用了損失函數的如下性質:當損失函數(3)式中的后處理函數fj均為一次函數,且參數化酉門Vl(θl)=Πke-iθkAk/2中的生成元Ak滿足=I時,固定其他參數,損失函數C是任一參數的周期為 2π 的正弦函數.基于此,量子序列最小優化方法在優化參數時,可以選取一個或一組參數并固定其他參數,直接將選取的參數調至當前最優,隨后對所有參數重復這一過程直至收斂.相比于傳統的梯度下降法,量子序列最小優化在一些VQE問題中具有更快的收斂速度.

2.4 解析梯度

混合量子-經典算法的一大優勢在于其損失函數的梯度可以在量子設備上直接計算.不失一般性,假設損失函數不包含對測量結果的經典后處理:

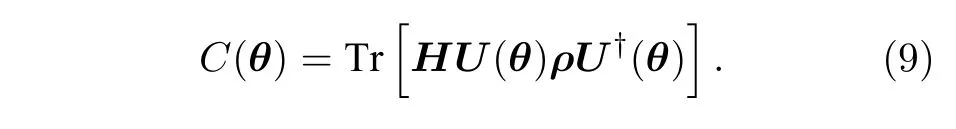
顯然,包含經典后處理的損失函數可以利用鏈式求導法則得到.

參數平移規則[39,40]是計算混合量子-經典算法中解析梯度的基本工具.該規則表明,當參數化酉門Vl(θl)=Πke-iθkAk/2中的生成元Ak滿足=I時,形如(9)式的損失函數對參數θk的偏導為

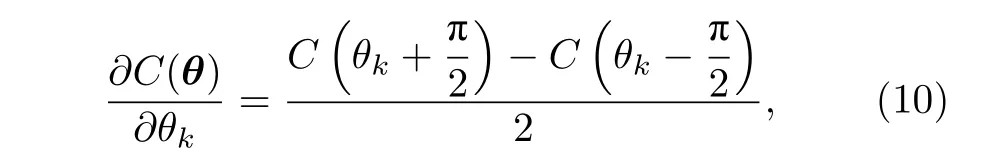
式中C(θk±π/2)表示C中參數θk±π/2 而其他參數保持不變.因此,通過改變目標參數后計算兩次電路的輸出,可以得到損失函數關于目標參數的梯度值.進一步地,在一些基于梯度的優化算法中需要用到高階導數信息(如黑塞矩陣等),此時反復利用參數平移規則即可求解相應的高階導數.

除參數平移規則之外,另一種計算參數的方法[41]將偏導式(10)表示為

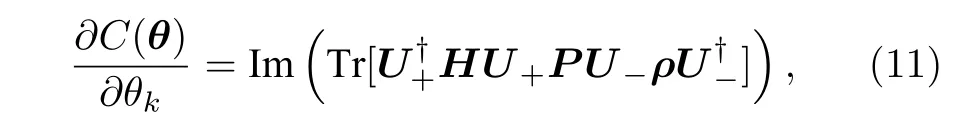
式中U-(U+)表示參數θk對應的參數化酉門之前(之后)的電路,即U-=Ul(θl)···U1(θ1),U+=UL(θL)···Ul+1(θl+1).因此,當P也是酉算符時(P通常為局部泡利算符),梯度值也可以通過引入一個輔助比特經由哈達瑪測試(見2.1 節)計算得到.

最后簡單介紹量子自然梯度中的Fubini-Study度量張量的近似計算[35].文獻[35]表明,Fubini-Study 度量張量有分塊對角矩陣近似g=diag(g(1),g(2),···,g(L)),且對角子矩陣g(l) 的矩陣元滿足

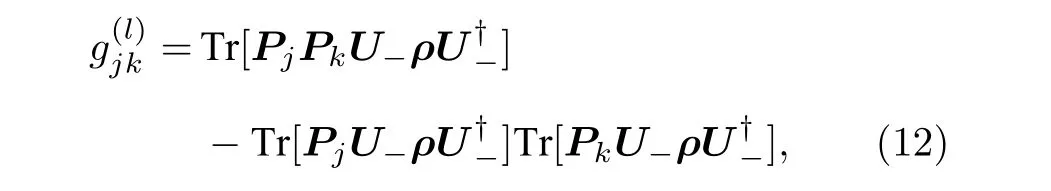
可見,通過對電路運行結果進行測量可以直接得到度量張量的分塊對角矩陣近似.

2.5 計算精度

本節的最后簡單討論混合量子-經典算法中計算損失函數時達到的精度與所需的測量次數.不失一般性,設待計算的損失函數為C=Tr[Hρout],其中ρout表示電路輸出量子態.由于量子力學的內稟隨機性,損失函數C實際上通過測量結果估計得到.為此,首先將H分解到泡利測量算符上:.隨后,損失函數C可按如下方式估計:

1) 在泡利算符Pj上對ρout進行T次測量.由于泡利測量只有兩種測量結果,記+1 結果出現的次數為M0,—1 結果出現的次數為M1,記Xj(1)=(M0-M1)/T.

時,估計誤差有 1-δ的概率小于?,即Pr[≤?]≥1-δ.因此,當m=O(poly(n)) 時,損失函數可以通過測量在量子設備上以任意精度高效地估計.

3 應用實例

3.1 譜信息估計

由于物理粒子的密度算符、哈密頓量等物理量的矩陣描述都是厄米特矩陣,粒子的各種特性往往能被對應物理量的譜信息(本征值)很好地描述;另一方面,量子電路模型也能直接處理密度矩陣(量子態)和哈密頓量(可觀測量).因此,對厄米特矩陣的譜信息估計是混合量子-經典算法的一個重要也是直接的應用.

VQE 是譜信息估計中最典型的一個例子.在VQE 中,基態能量直接對應厄米特矩陣的最小本征值;同時,VQE 基于“對任意量子態的測量值的期望都不小于最小本征值”這一性質設計損失函數,從而成功求解基態能量.受VQE 啟發,提取更多譜信息的混合量子-經典算法被相繼提出.

3.1.1 子空間搜索-量子變分本征求解器

子空間搜索-量子變分本征求解器(subspace search VQE,SSVQE)[43]是VQE 算法的一個直接拓展.SSVQE 求解目標哈密頓量的基態以及前K-1個激發態能量,亦即求解厄米特矩陣最小的K個本征值.在SSVQE 中,損失函數對K個正交單位向量(通常選取計算基向量)經過參數化電路后的測量值加權求和:

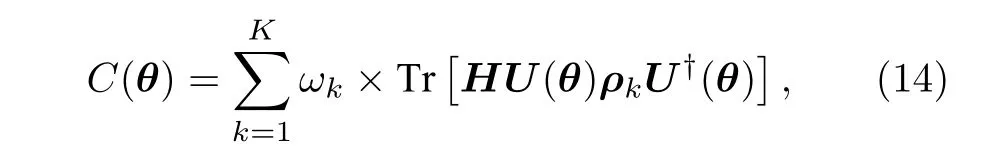
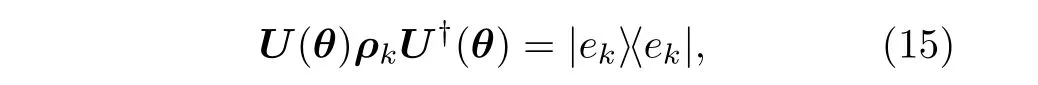
其中|ek〉為H第k小個本征值對應的本征向量,即H的第k激發態.因此,當損失函數優化到最小時,測量得到Tr[HU(θ)ρkU?(θ)]即為厄米特矩陣第k小個本征值,亦即待求的基態或激發態能量.

3.1.2 變分量子態對角化

對混態的譜分解(對角化)有助于我們理解量子態的糾纏性質.變分量子態對角化(variational quantum state diagonalization,VQSD)[44]算法求解酉變U使得目標態ρ經過酉變后在計算基上對角化,即.在VQSD 中,記=U(θ)ρU?(θ),損失函數提供了兩種設計:

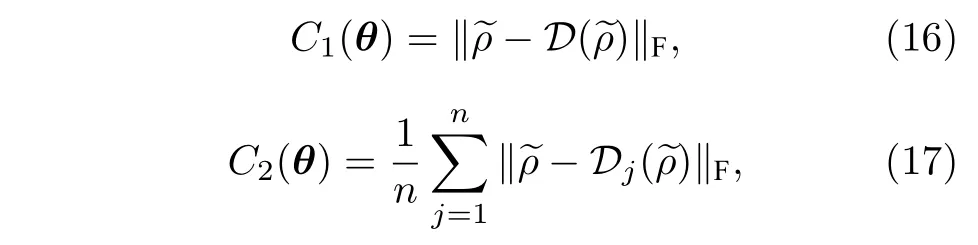
其中D表示整個輸入量子態上的(完全)去極化信道,Dj表示僅對第j個量子比特作用的(完全)去極化信道.顯然C1和C2等于0 當且僅當ρ～ 實現了對角化.因此,通過優化損失函數至0 即可完成量子態的對角化.同時,文獻[44]分別設計了兩種電路用于計算兩個損失函數.文獻[44]指出,由于C1擁有更簡單的計算電路,而C2擁有更好的可訓練性,在實際訓練中可以根據量子比特數對兩種損失函數進行加權求和作為最終的損失函數.

值得一提的是,由于哈密頓量和輸入量子態在損失函數中具有對偶性,3.1.1 節SSVQE 中對正交量子態加權求和的技巧也可用于量子態對角化,如文獻[20]就基于該技巧實現了量子態的本征值求解.

3.1.3 變分量子奇異值分解

奇異值分解作為譜分解的擴展,在數據壓縮、推薦系統等領域具有重要應用.變分量子奇異值分解(variational quantum singular value decomposition,VQSVD)[45]實現任意方陣M的奇異值分解.VQSVD 中,損失函數定義為

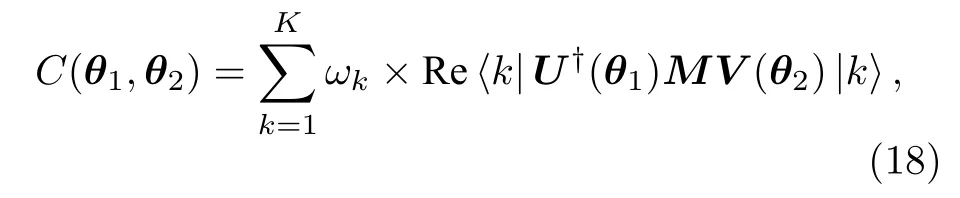
其中是一組互相正交的純態,ωk是嚴格單調減小的正實數序列.文獻[45]證明上述損失函數取到最大值當且僅當

此外,由于對兩方糾纏態的施密特分解等價于糾纏態向量重排矩陣的奇異值分解,文獻[46]通過對優化兩個局部參數化電路實現施密特分解.本質上,文獻[46]和VQSVD 相當于對待分解的矩陣采用了不同的編碼方式:VQSVD 將矩陣分解為酉算符的線性組合,而文獻[46]相當于將矩陣重排為兩方量子態對應的向量.

3.1.4 跡范數估計

3.2 距離估計

在量子設備上制備特定的量子態是一項重要的基本能力,例如在變分量子本征求解器中任務的目標即可認為是制備一個量子系統的能量基態.在制備量子態后,離不開驗證和刻畫的過程.在這之中就會涉及到量子態之間距離估計的函數.這里主要討論常用的兩種距離估計函數[47],即跡距離D

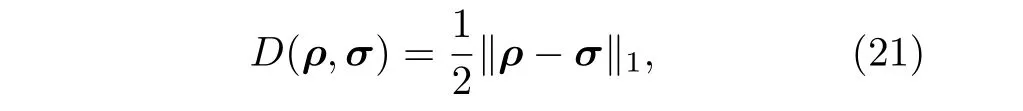
以及態保真度F

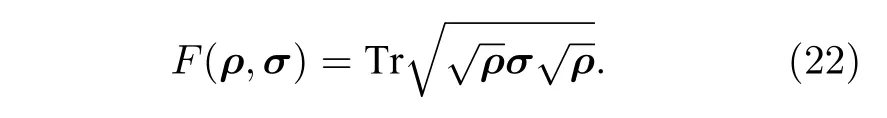
3.2.1 跡距離估計

由于對一般量子態間的跡距離的大小判斷屬于QSZK-complete 復雜度類[50],而QSZK (quantum statistic zero knowledge)包括了BQP (bounded-error quantum polynomial time)復雜度類,因此即使在量子計算機上跡距離的估計目前也不存在高效算法.由于跡距離具有如下性質:

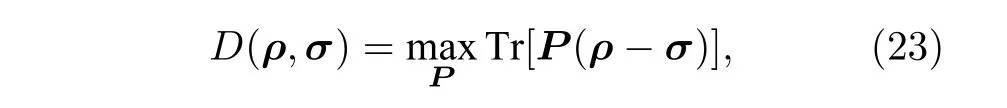
其中P的優化范圍是所有POVM 元(滿足0 ≤P≤I的半正定矩陣),文獻[49]基于該性質,并通過奈馬克擴張定理引入一個輔助比特,將POVM元的優化轉化為酉矩陣上的優化,證明跡距離滿足

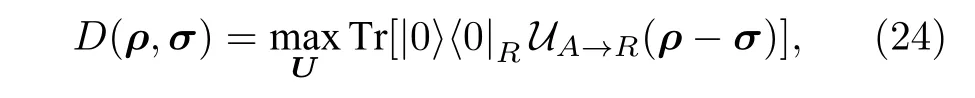
其中UA→R(XA)=TrA[U(XA ?|0〉〈0|R)U?] .因此,通過最大化損失函數C=Tr[|0〉〈0|R UA→R(ρ-σ)]即可得到ρ,σ間的跡距離估計.值得一提的是,在文獻[49]中,(24)式由(20)式令H=1/2(ρ-σ)直接得到.

3.2.2 保真度估計

用經典方法計算保真度F需要先對量子態ρ和σ進行量子態層析來獲取密度算符的矩陣表示,然后在經典計算機上按照(22)式進行計算.由于希爾伯特空間維度隨著量子比特數呈指數增長,這種方法通常認為是困難的.隨之而來的問題就是,在量子設備上直接估算態保真度是否可行,是否更高效.這種思路下的主要問題在于保真度計算公式中涉及到對量子態的非整數冪的操作,沒有已知的量子算法可以精確完成這一任務.針對這一問題,文獻[20]提出了一種混合量子-經典算法用于近似任意混合態σ和低秩態ρ之間保真度的方案(variational quantum fidelity estimation,VQFE),并給出對保真度估計的上下界.其主要原理是通過對ρ對角化獲取其在本征子空間上的譜信息然后計算σ在該基組表示下的矩陣元素從而得到對保真度的估計.進一步地,文獻[49]基于烏爾曼定理(Uhlmann’s theorem)給出了計算任意混合態之間保真度的方式.通過純化子程序,先分別獲得需要測量保真度的兩個量子態ρA和σA的純化態|ψ〉AR和|φ〉AR.然后通過純化中輔助量子比特的自由度以及經典優化算法去最大化兩個純化態之間的態重疊,即可獲得對保真度的估計:

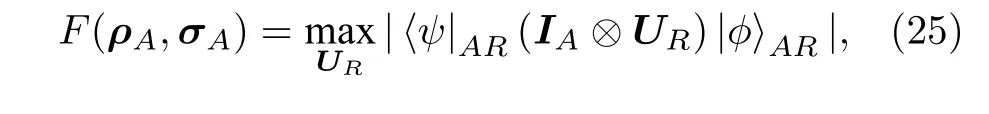
其中A表示原始問題的空間,R表示純化子程序中引入的輔助量子比特的空間.

3.3 組合優化問題

組合優化問題是指從離散的可行解集合中找出最優的一個解,如旅行商問題、最大割問題等著名的NP 困難問題都屬于組合優化問題.這些問題都可以抽象為最小化(或最大化)一個目標函數D(x),其中x為一組離散的二進制變量.

要在量子計算機上解決經典組合優化問題,需要先把它轉化成量子優化問題.最直接的做法是將原問題的目標函數D(x)編碼為哈密頓量HD,使得該哈密頓量的基態對應原優化問題的解[51].這樣,組合優化問題就變成了求解哈密頓量基態的問題,即找到一個量子態|ψ〉使得

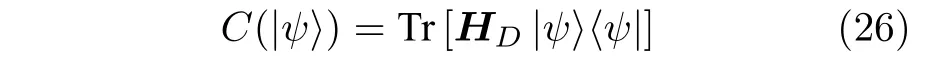
最小,而這正是混合量子-經典算法擅長的.根據VQE 的思想,可以利用參數化量子電路尋找態|ψ(θ)〉=U(θ)|s〉,其中量子態|s〉為量子電路運行前的初始態,θ為量子電路中可優化的參數.

量子近似優化算法(quantum approximate optimization algorithm,QAOA)[13]提供了一種設計參數化量子電路的思路,該算法最初由Farhi等[52]提出,專門用于解決組合優化問題.與量子絕熱算法(quantum adiabatic algorithm,QAA)[52,53]類似,QAOA 受到絕熱定理的啟發,構造類似絕熱演化的參數化量子電路來求解哈密頓量HD的基態.根據絕熱定理,如果一個系統的哈密頓量隨時間的演化由H(t)=(1-t/T)HB+tHD/T給出,且初始時該系統處于哈密頓量HB的基態,那么通常經過足夠長的演化時間T,系統最終會處于哈密頓量HD的基態.因此,只需要準備一個基態易于制備的輔助哈密頓量HB,將其基態作為初始量子態借助Trotter 乘積式來近似演化哈密頓量H(t),最終便能得到哈密頓量HD的基態,也即原組合優化問題的最優解.這個演化過程可以近似為如下的參數化酉變:

其 中,UD(γj)=e-iγjHD和UB(βj)=e-iβjHB分 別是哈密頓量HD與哈密頓量HB對應的參數化酉變;γ,β是可以優化的參數;p則是參數化酉變的層數.

事實上,QAOA 的思想不僅可以解決組合優化問題,由其推廣得到的一類參數化量子電路,即量子交替算符擬設電路,可廣泛應用于其他問題[9].

3.4 量子機器學習

量子機器學習就是量子算法和機器學習的有機結合.經典的神經網絡分為兩部分:神經網絡和優化器.而量子機器學習,就是把經典的神經網絡換成量子的神經網絡并由量子計算設備執行,并且在經典設備上進行量子神經網絡的參數優化,即使用經典的優化器去優化量子神經網絡.通常情況下,量子神經網絡是由參數化量子電路表達的.量子機器學習有望利用量子的并行運算的特性對經典的機器學習算法進行加速.下面討論幾種較為常見的量子機器學習問題:量子分類器[31,39,41,54]、量子生成對抗網絡[55,56]和量子自編碼器[57,58].

3.4.1 量子分類器

在機器學習中,分類問題是極其重要的監督學習問題.分類過程實質上是一個給數據貼標簽的過程,當輸入數據滿足某個條件的時候,就給該數據貼上相應的標簽,從而完成分類.分類問題通常會給定一個訓練包含N個樣本的數據集{(x(k),,其中x(k)是數據點,y(k) 是數據的標簽.該任務的目的是通過訓練數據集訓練神經網絡,使得該神經網絡在遇到沒有處理過的數據時能夠做出正確的分類.在量子分類器的框架下,量子神經網絡主要表達形式為參數化量子電路,Mitarai 等[39]以及Farhi 和Neven[41]采用參數化量子電路的結構分別完成了二分類任務和手寫數字的分類任務.

通常情況下,給定的數據集是經典的數據,所以分類器第一步需要做的便是把經典數據編碼成可在量子設備上可以執行的量子數據(量子態),即x(k)→|ψ〉(k).下一步需要把參數化量子電路U(θ)作用在編碼后的量子態上,由此得到U(θ)|ψ〉(k) .隨后,把損失函數定義為真實標簽和某個可觀測量O的期望值的距離,即

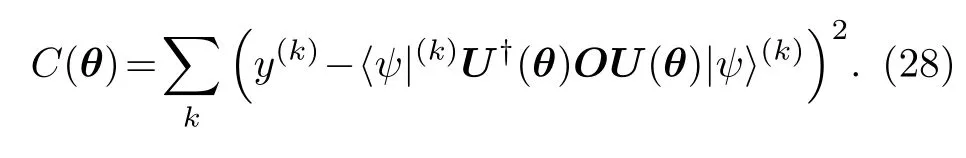
使用經典優化器對損失函數進行優化,通過不斷調整參數化量子電路中的參數,使得損失函數收斂至最小值.值得注意的是,編碼方法以及量子神經網絡結構并不唯一.合理的編碼方式和神經網絡能夠提高分類器的運行速度和預測準確性,因此,針對不同的問題,應比較并選用更優的編碼方式.目前常用的編碼方式[59,60]包括基態編碼、振幅編碼、角度編碼和IQP 編碼.關于神經網絡表達能力將在4.2 節詳細討論.

值得一提的是,文獻[31]提出了影子量子學習方法,利用作用在局部量子比特上的影子電路實現多分類任務.數值實驗結果表明,相比于已有的量子分類算法,該算法具有更強大的分類能力,同時大幅減少了網絡參數,降低了訓練代價.此外,量子核方法[59,61-63]也是實現量子分類器的可行方案.和經典核方法一樣,量子核方法也是先通過特征映射把原始數據映射到特征空間里,然后尋找超平面把數據分類.從理論上來說,相較于經典的核方法,量子核方法在處理分類問題時有平方級的加速效果[64].

MNIST 作為常用的數據集,常常在分類任務中作為基礎測試的數據集.Wang 等[65]在光量子平臺上實現了對MNIST 數據集中的手寫“0”和“1”進行分類,三層結構的分辨準確率達98.58%,五層結構的分辨準確率達99.10%.在影子量子學習方法中,本課題組使用35 個參數使得MNIST的二分類任務準確率達到99.52%.而在MNIST十分類任務中,在使用928 個參數的情況下,準確率達到 87.39%[31].

3.4.2 量子生成對抗網絡

生成對抗網絡(generative adversarial network,GAN)[66]在經典學習中扮演著重要的角色.GAN 通常由生成器和判別器兩部分組成,其中生成器接受隨機的噪聲信號,以此為輸入來生成期望得到的數據;判別器判斷接收到的數據是不是來自真實數據,通常輸出一個P(x),表示輸入數據x是真實數據的概率.

量子生成對抗網絡[55,56,67](quantum generative adversarial network,QGAN)的目的是利用量子計算設備加速經典生成對抗網絡的訓練.相比于GAN,QGAN 生成的是量子態,而不再是經典數據.在QGAN 的框架下,生成器G和判別器D分別對應著兩個參數化量子電路UG和UD.生成器的目標是最小化損失函數,從而達到生成的數據以假亂真的效果;判別器的目標是最大化損失函數,要盡可能地分辨出哪些是真實數據,哪些是生成器生成的數據.可以把訓練過程視為博弈的過程,訓練的結果會使得生成器和判別器達到納什均衡點,即生成器具備了生成真實數據的能力,而判別器也無法再區分生成數據和真實數據.一般情況下,量子對抗生成網絡的優化函數都可以寫成以下形式:

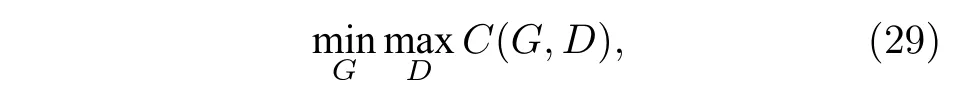
其中C根據任務的不同而相應變化.值得注意的是,實際過程中,通常采用交替訓練的方式,即先固定G,訓練D,然后再固定D,訓練G,不斷往復.當兩者的性能足夠時,模型會收斂,兩者達到納什均衡.

QGAN 由經典的GAN 發展而來,所以QGAN也繼承了經典GAN 的不足,比如訓練不穩定、訓練效果局限于網絡框架等.在經典領域,WGAN(Wasserstein GAN)[68]解決了GAN 的缺陷.相應地,在量子領域,QWGAN (quantum Wasserstein GAN)[69]的提出也提升了QGAN 效果.如今,量子對抗生成網絡的方法已經被應用到各種任務上,比如概率分布的學習[70-72]、量子態的學習[56,73]、量子電路的學習[69]以及糾纏的探測[74].

3.4.3 量子自編碼器

量子自編碼器和經典自編碼器一樣,都是由編碼器和解碼器組成,是用于壓縮數據,進行特征降維的一種算法.在量子自編碼器中,輸入的數據為復合量子系統AB的量子態ρAB.將編碼器E=U(θ)(即參數化量子電路)作用在量子態上,得到U(θ)ρABU?(θ).該步驟將量子系統AB的信息編碼到量子系統A上.對于量子系統B,只需要對他們進行測量并丟棄即可,即ρ?A=TrB(U(θ)ρABU?(θ)).至此,已經完成了信息的壓縮.在進行解碼時,需要引入與系統B維度相同的系統C,并且固定其量子態ρC.隨后將解碼器D=U?(θ) 作用在整個量子系統A+C上,得到還原后的量子態=U?(θ)[ρc ?TrB(U(θ)ρABU?(θ))]U(θ)[57].

在量子自編碼器中,損失函數一般有兩種定義方法:

1) 由于量子自編碼的任務是對數據進行編碼并解碼,希望輸出的量子態ρout和輸入的量子態ρin盡可能地相似,所以損失函數定義為兩個量子態之間的保真度F,即

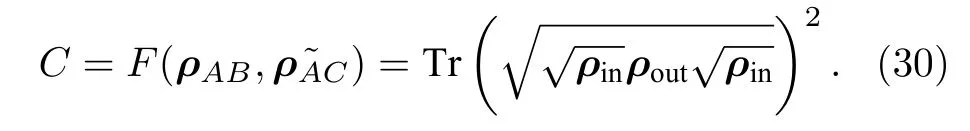
2) 在還原被壓縮信息的時候,需要引入另一個固定的純態量子系統C,與系統A進行耦合.相對應地,壓縮過程可以理解為量子系統A和量子系統B解耦的過程,由此可以定義損失函數為壓縮后的量子系統和引入的量子系統ρC之間的保真度,即

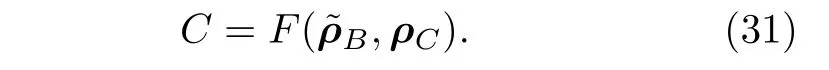
值得注意的是,待編碼的量子態所包含的糾纏資源量在一定程度上決定了量子自編碼器的效果.簡單地說,如果量子態ρAB含有的量子資源超過了量子系統A所能容納的上限,那么量子自編碼器必然會導致信息的損失.文獻[58]設計了一種可以在量子退火機上運行的絕熱算法進行量子信息的壓縮.和其他的量子自編碼器相比,該算法充分利用了測量所得到的信息,在一定程度上解決了信息損失的問題.

3.5 量子糾錯

量子糾錯[75-77]可表示為如下過程:1)編碼信道U將k個邏輯量子比特的量子態|Ψ〉編碼到n個物理量子比特,得到邏輯量子態|Ψ〉L;2)邏輯量子態|Ψ〉L經過噪聲信道N,該噪聲信道由具體硬件設備決定;3)糾錯信道W嘗試糾正噪聲對邏輯量子態的影響,該信道使用輔助量子比特探測并糾正錯誤;4)解碼信道U?(編碼信道U的逆)從物理比特解碼還原量子態.整個過程如圖4所示.編碼信道U和糾錯信道W決定該糾錯方案的性能:復合信道U??W ?N ?U和理想無噪信道越接近,糾錯效果越好.然而設計高效的糾錯方案是極具挑戰性的任務.近年來,研究人員嘗試利用經典機器學習技術提高量子糾錯效率[78-88],這類工作屬于典型的混合量子-經典算法.使用混合量子-經典算法實現量子糾錯的優勢在于構造參數化電路時可以綜合考慮硬件設備的特點,比如所支持的量子門類型以及拓撲結構等,設計出更高效的硬件相關的糾錯方案.下面介紹兩個具有代表性的探索工作.

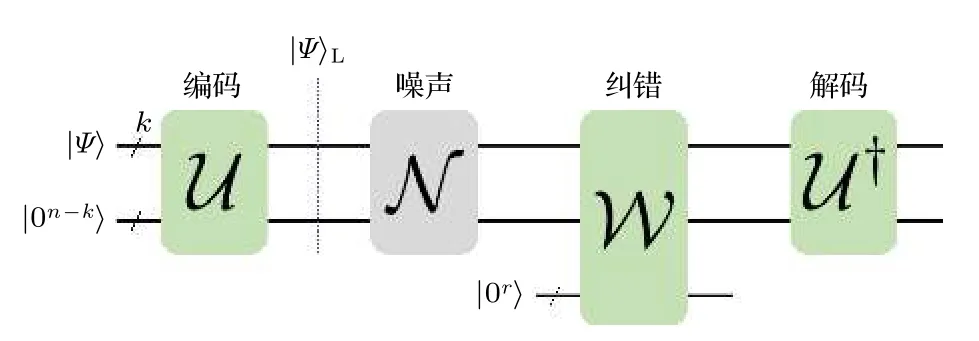
圖4 量子糾錯基本框架:量子態 |Ψ〉使用編碼信道 U 編碼,經過噪聲信道 N后使用糾錯信道 W糾正錯誤,最后使用解碼信道 U? 解碼,還原輸入量子態Fig.4.Framework of quantum error correction.The quantum state |Ψ〉 first is encoded by the encoding channel U,then passes the noise channel N,and then is corrected by the correction channel W,finally is recovered by the decoding channel U? .

文獻[78]提出量子變分糾錯算法QVECTOR(variational quantum error corrector).該方法的基本思路是將如圖4 所示的編碼信道U和糾錯信道W表示為參數化量子電路U(·)=U(θ1)(·)U?(θ1)和W(·)=W(θ2)(·)W?(θ2) .我們期望復合信道U?(θ1)W(θ2)NU(θ1) 等效或者逼近理想無噪信道,因此定義如下形式的平均保真度作為損失函數:

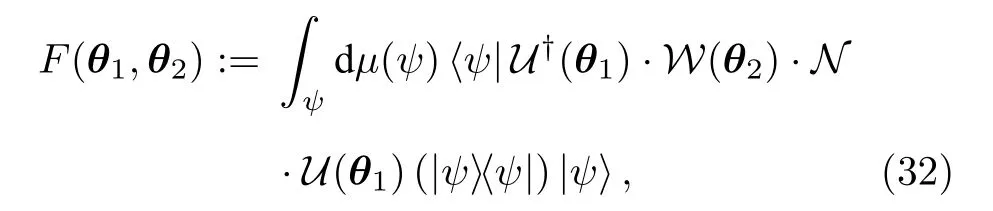
其中μ(ψ) 表示哈爾測度.直觀上而言,該損失函數刻畫了上述糾錯方案在輸入量子態上的平均表現行為.當F(θ1,θ2)=1 時,對應的參數化量子電路U(θ1)和W(θ2)實現了對噪聲信道N的完全糾錯.可采用更高效的酉2-設計[89]或近似酉2-設計[90]進行隨機采樣量子態來估計損失函數(32)式.實驗數據表明,相對五比特量子糾錯碼[91,92],QVECTOR算法在處理特定噪聲時有更好的效果.

由圖4 可知,設計合適的編碼信道U精確地制備邏輯量子態|Ψ〉L是量子糾錯中的關鍵任務.文獻[79]提出使用混合量子-經典算法制備|Ψ〉L,其核心思想是分析|Ψ〉L的數學性質將之編碼為某個哈密頓量H的基態本征向量,調用變分量子本征求解器求解H的基態能量和本征向量,對應的參數化量子電路即為編碼信道.該方法的關鍵步驟是構造哈密頓量H.下面以穩定子碼[93]為例給出H的構造方法.假設S為某單量子比特糾錯碼的穩定子碼且其穩定子為S=〈g1,···,gK〉.著名的例子包括五比特量子糾錯碼[91,92]、Steane 糾錯碼[94]和Shor 糾錯碼[95].由穩定子碼定義可知,對任意k=1,···,K均有表示|Ψ〉L的正交態,定義算符,易見OL|Ψ〉L=|Ψ〉L.算符OL編碼邏輯量子態|Ψ〉L的系數信息.定義哈密頓量

3.6 其他應用

本節介紹3 種不直接屬于上述分類但具有代表性的混合量子-經典算法.選擇這些算法的原因在于它們使用的技巧具有一定代表性和啟發性.

3.6.1 量子線性求解器

變分量子線性求解器(variational quantum linear solver,VQLS)[96-98]實現線性方程組Ax=b的求解.不失一般性,假設b是歸一化的.VQSL首∑先將矩陣A分解為酉矩陣的線性組合A=,隨后根據歸一化向量b制備對應的量子態|b〉,并將|0〉態輸入參數化電路得到|x〉=U(θ)|0〉,然后最小化損失函數:

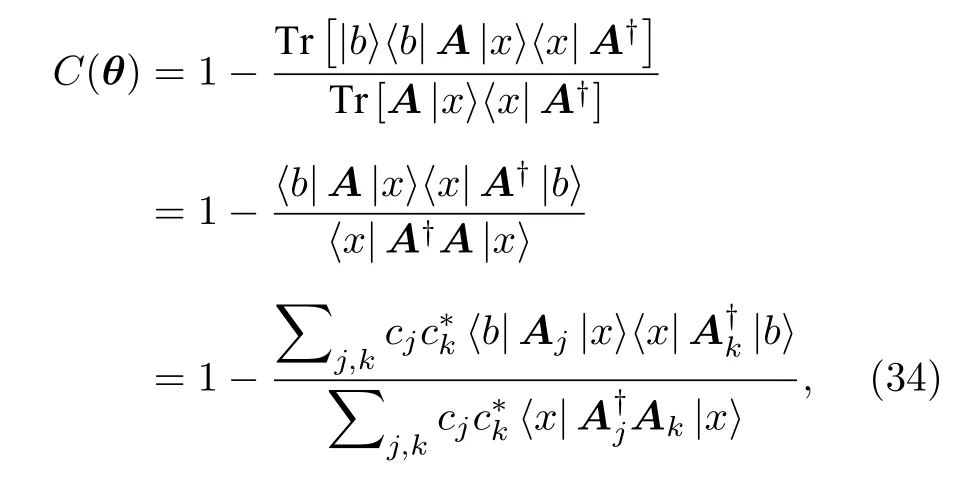
3.6.2 糾纏檢測

變分糾纏檢測(variational entanglement detection,VED)[99]利用了轉置映射的準概率分解[100].對于密度矩陣,轉置映射T將其映射為.對于兩方量子態ρAB,量子糾纏存在的一個充分條件是ρAB在B系統上部分轉置后的最小本征值小于0,這種方法被稱為PPT 準則(positive partial transpose criterion)[101].據此,VED 通過估計ρAB部分轉置后的最小本征值檢測兩方糾纏.由于轉置映射不是完全正的,不能在物理設備上直接實現,文獻[99]將轉置映射分解為泡利門的線性組合,隨后基于準概率分解對電路進行隨機采樣得到相應損失函數的無偏估計.文獻[99]同樣給出了其他糾纏判定條件對應映射的泡利門分解.

3.6.3 吉布斯態制備

吉布斯態是量子模擬、多體物理研究等諸多領域的關鍵步驟.給定哈密頓量H,其對應的吉布斯態表示為

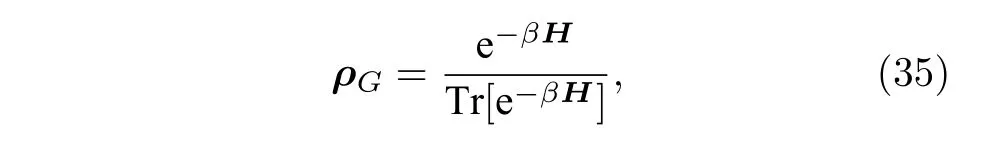
其中β=1/(kBT) .由于吉布斯態使得系統自由能最小:

其中S為量子態ρ的馮諾依曼熵S(ρ)=-Tr[ρlogρ],基于該性質可以設計混合量子-經典算法,通過最小化自由能制備吉布斯態.對于量子態的自由能在量子設備上的估計,文獻[102,45]分別提供兩種方法:文獻[102]將馮諾依曼熵中的對數運算展開成三角級數并截斷,隨后設計電路估計自由能;而文獻[45]直接將馮諾依曼熵展開成泰勒級數并截斷,隨后利用交換測試計算態重疊和高階態重疊(即Tr[ρ2] 和 Tr[ρ3]),從而估計自由能.

3.6.4 虛時演化

虛時演化[103]是研究量子系統的工具,被廣泛應用在許多物理領域,包括量子力學、統計力學和宇宙學.在實時演化中,一個哈密頓量為H的量子系統的傳播函數為 e-iHt.在虛時演化中,由于時間τ=it為虛數,該系統的傳播函數為 e-Hτ.顯然,演化的時間越長,系統的能量也就越低,最終會穩定在系統的基態能量E0,即τ →∞,Esys→E0.因此,虛時演化算法可用于求解子系統的基態.由于虛時演化過程是數學的而非物理的,如何模擬演化過程是虛時演化算法的關鍵.

基于虛時演化的特殊性質,文獻[104,105]提出了使用變分量子電路對虛時演化進行模擬,并計算化學系統的基態能量.首先,需要制備一個追蹤態|ψ(θ(τ))〉=V(θ(τ))|0〉,其中,V(θ(τ))=UN(θN)···Uk(θk)···U1(θ1)代表著一系列酉門,這里可以把V(θ(τ))當作參數化量子電路.當τ=0時,代表著量子系統的初始態.隨后,對V(θ(τ)) 的各個參數進行更新

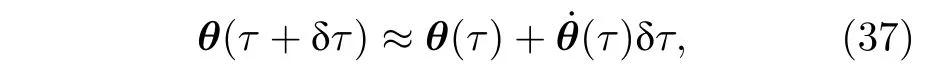
其中(τ) 是量子電路的自然梯度.隨后通過迭代NT=τtotoal/δτ次,來模擬虛時從τ=0→τ=τtotal的演化過程.當模擬的時間足夠長時,便能夠得到系統哈密頓量H的期望值的最小值,即

4 挑 戰

盡管混合量子-經典算法已經在理論和實踐上被證明在求解特定問題時具有高效的表現,該領域仍然存在若干開放性問題與挑戰.本節主要介紹3 種對混合量子-經典算法效果的制約因素和潛在的解決思路,分別為噪聲影響、電路表達能力以及可訓練性.

4.1 噪聲影響

作為一類NISQ 算法,噪聲對混合量子-經典算法的影響值得深入研究.大體上,量子噪聲可以分為相干噪聲和非相干噪聲.相干噪聲的產生可能是由于硬件校準的精度,導致在執行一個量子門U(θ)時實際執行的是U(θ+δ) .通常來說,相干噪聲對于經典優化方法來說并不構成很大的影響,特別是SPSA 這種本身就會對參數產生隨機擾動的優化方法.量子設備的非相干噪聲往往會對損失函數的整體景觀產生影響,使其變得平坦或改變最值的位置,如圖5 所示.文獻[106]和文獻[107]分別從數值和理論上研究了泡利噪聲對QAOA 算法的影響,并指出QAOA 算法對低強度泡利噪聲具有一定抗性;文獻[108]進一步探究了QAOA 算法的誤差上界與噪聲和量子Fisher 信息相關;文獻[109]指出泡利噪聲直接導致混合量子-經典算法的梯度消失問題;文獻[110]表明,在一部分計算任務中(如變分量子編譯),盡管噪聲使得損失函數整體變得平坦,但不會影響最優參數的取值,因此不影響算法最終結果的正確性;文獻[111]表明噪聲會破壞參數空間的對稱性,導致部分全局最優解變為局部最優,從而增加優化難度;文獻[112]對比了有噪條件下混合量子-經典算法和經典算法的復雜度,證明了在大噪聲條件下混合量子-經典算法相比于經典算法不再具有優勢.

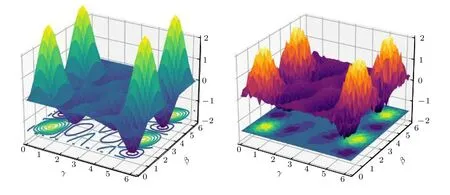
圖5 無噪(左)與有噪(右)條件下損失函數景觀對比Fig.5.Comparison between noise-free (left) and noisy (right) cost function landscape.

4.2 電路表達能力

2.2節曾提到,在參數化量子電路的模型設計中,為使參數空間能夠對應盡可能多的酉變,從而使優化過程覆蓋盡可能大的解空間.參數化量子電路的表達能力可直觀地理解為電路取遍所有參數時能表達的酉變范圍的大小.一般來說,更深的電路具有更強的表達能力,但電路深度同時會帶來更嚴重的噪聲和可訓練性問題.因此,如何權衡電路深度與表達能力,以及如何設計表達能力更強的電路模型是混合量子-經典算法面臨的重要一項挑戰.

目前,一種電路表達能力定義基于電路輸出量子態的平均高階張量積和對應哈爾積分之間的Frobenius 距離.由于該距離與電路輸出量子態對間的保真度分布直接相關,最終采用參數化電路與哈爾分布輸出的保真度分布之間的K-L 散度對電路U(θ) 表達能力進行量化:

其中DKL(A‖B)表示概率分布A,B之間的K-L 散度;P(U,F)表示電路U在輸入|0〉且參數θ成隨機均勻分布時,隨機輸出的一對量子態間的保真度的概率分布;PHaar(F) 表示一對滿足哈爾分布的隨機量子態間的保真度的概率分布且有解析表示:PHaar(F)=(d-1)(1-F)d-2;d是系統希爾伯特空間的維度.由于P(U,F) 可以通過對電路參數采樣后測量估計,表達能力因此可以在近期設備上有效計算.文獻[25]首先定義并計算了若干常用參數化電路模型的表達能力;文獻[113]進一步比較了常見的硬件高效擬設與交錯分層擬設的表達能力,指出后者相較于前者,在提供更強的可訓練性的同時保留了幾乎相當的表達能力.文獻[114]從理論角度證明了損失函數的梯度方差的上界與電路表達能力有關.

值得一提的是,文獻[25]基于梅爾-沃勒克度量定義了電路的糾纏能力,即電路平均能提供多少糾纏.電路糾纏能力在一些量子態制備任務中起到關鍵作用.

4.3 可訓練性

目前混合量子-經典算法的可訓練性主要指的是由貧瘠高原現象對優化過程造成的困難.貧瘠高原(barren plateau)現象[115]最早于2018 年被提出,當混合量子-經典算法所選取的非結構化的擬設電路U(θ) 進行隨機參數初始化時,算法對應損失函數C(θ) 的梯度方差在采樣的平均意義下會隨著問題規模n的擴大呈現指數遞減.直觀來看,這種現象會使得問題的優化曲面變得非常平坦(故稱貧瘠),從而使得為了達到確定優化方向的計算精度所需的測量數變得非常巨大(如果無法達到測量精度要求,電路的優化過程可能會接近于隨機游走),最終導致基于梯度或者非梯度的優化方法[116]都很難找到全局最小值.產生這種現象背后的數學原因在于非結構化的電路在隨機初始化參數時滿足酉2-設計的性質[117].相關證明和避免貧瘠高原現象的理論研究也是圍繞這個核心性質展開的.值得注意的是,文獻[115]中的結果部分表明了4.2 節中提到的電路表達能力和可訓練性之間的權衡關系.當電路的深度增加時相應的表達能力增強,但同時梯度的方差(可訓練性)也會逐漸減小.

近些年,隨著對混合量子-經典算法的深入研究,相應的可訓練性解決方案也在陸續提出.針對貧瘠高原現象,文獻[118]提出了一種初始化參數θ的方案.其核心思想在于通過先選取部分參數隨機初始化,然后特定剩下的參數使得整個電路由一系列的單位陣構成.這樣可以減少電路中的隨機性從而破壞酉設計的性質獲取可訓練性.文獻[119]進一步提出了分層訓練的方案,即使用若干初始層訓練然后依次添加電路結構和層數.除了上述通過設計初始化訓練方案,基于特定問題啟發設計的電路結構[9,120]通常認為對于大規模的問題依然是可以訓練的.此外,3.1.2 節提到的通過重新設計損失函數將其表達為局部損失函數的形式(只同時測量部分量子比特)[21]也被證明可以有效應對可訓練性問題.然而很多算法的損失函數是否存在這樣的表達形式依然未定.最后,有研究表明噪聲[109]和過度的糾纏能力[121]也會造成類似現象并阻礙訓練過程.可以說,可訓練性問題至今依然是混合量子-經典算法長遠發展的一大挑戰.

5 總結與展望

本綜述介紹了混合量子-經典算法的基本概念,此類算法在量子化學、機器學習、組合優化、量子信息等領域的研究進展以及算法目前面臨的主要挑戰.一方面,可以看到混合量子-經典算法已為許多領域問題提供了有效且具備潛在優勢的解決方案,同時可以結合優化理論和機器學習中的現有技術,盡可能在近期量子設備上發揮量子計算的能力,推動量子計算與機器學習的融合創新.另一方面,我們也認識到混合量子-經典算法作為一個相對“年輕”的研究方向存在若干瓶頸,包括對電路表達能力的理論分析工具不夠完善,對算法規模的可擴展性有限,大部分算法的量子優勢缺乏嚴格的理論和實驗證明等.如何克服這些混合量子-經典算法的瓶頸以及探索其在更多領域的應用,將是混合量子-經典算法未來重要的發展方向.此外,張量網絡作為連接經典與量子計算的數學模型,已經從理論[122,123]和應用[124,125]層面啟發了機器學習領域的許多研究方向.因此,這一工具在近期量子設備上的探索同樣值得關注.隨著量子硬件能力的不斷提升與混合量子-經典算法技術的不斷發展,相信具有量子優勢的近期量子設備實用化應用將有望實現.