基于測量的量子計算研究進展*

2021-11-19 05:15:24張詩豪張向東李綠周

物理學報 2021年21期

張詩豪張向東李綠周?

1) (中山大學計算機學院,量子計算與計算機理論研究所,廣州 510006)

2) (北京理工大學物理學院,先進光電量子結構設計與測量教育部重點實驗室,北京 100081)

相比于量子門電路模型,基于測量的量子計算模型為實現普適量子計算提供了另一途徑,且經過近二十年的發展其內涵已得到了極大豐富.本文對基于測量的量子計算模型的研究歷史和現狀進行綜述.首先簡要介紹該模型的基本理論,包括量子圖態等資源態的概念和工作原理、模型的計算普適性和經典模擬方法、在相關量子信息處理領域的應用等.接著從量子物理特性的角度概括基于測量的量子計算模型和量子多體系統之間的緊密聯系,包括量子糾纏、互文性、量子關聯、對稱保護拓撲序和量子物質相等作為計算資源所發揮的獨特作用.然后,總結實現基于測量的量子計算模型的不同技術路線和實驗成果.這些理論和實驗方面的進展是不斷推動可擴展容錯量子計算機研制的力量源泉.最后,對該領域未來的研究方向進行討論和展望,希望能啟發讀者進一步學習和探索相關課題.

1 引言

量子計算與量子信息是當代科學的前沿,具有廣闊的發展前景[1].在現代量子信息科學中,有兩類物理內涵豐富且實驗可行的量子計算模型值得關注:1)基于幺正演化的量子門電路模型[2];2)基于測量的量子計算(measurement-based quantum computation,MBQC)模型[3,4].MBQC 模型在理論上和量子門電路模型等價,都可以實現普適的量子計算.就技術層面而言,MBQC 的實現僅取決于糾纏態的制備和對量子比特的測量操作,方便在光學和離子阱等體系中進行實驗演示[5,6].隨著量子技術的進步,MBQC 已用于構建量子Toffoli 門[7],演示量子算法[8-10],展示量子糾錯碼[11],執行基于測量的量子網絡編碼[12]等信息處理任務.

直觀地看,如果將量子門電路的構建比作逐塊搭建積木至目標結構,那么MBQC 的執行更像從一整塊木材中挖除多余部分以得到所要結果.因此,相比之下MBQC 在實現量子計算時往往需要用到更多的量子比特(quantum bit,qubit)資源,如執行3-qubit 量子傅里葉變換(quantum Fourier transform,QFT)需制備1 個33-qubit 糾纏圖態作為初始資源態[13].此外,量子電路的合成與優化有經典電路作為參照,而MBQC 沒有直接的經典模型對應,因而在量子算法的設計層面需要更多巧思.盡管在實現量子計算上存在這些挑戰,但人們發現MBQC 能與其他領域的研究相結合,如將圖論、量子糾纏理論、計算復雜性、物質拓撲相、統計物理等主題聯系起來,因而逐漸成為交叉領域的研究焦點[14].

本文從量子物理學和計算機科學的角度概括MBQC 模型的相關理論,包括MBQC 的基本原理、計算普適性及應用、相關衍生模型的計算特點及背后的物理屬性,并且梳理了不同技術路線下的實驗進展,探討了未來的潛在研究方向.希望能對當前帶噪聲中等規模量子(noisy intermediate-scale quantum,NISQ) 時代[15]下的研究有所啟示.

2 MBQC 的基本原理

2.1 量子計算的基礎概念

為了便于讀者更好地領會本文主旨,在正式介紹MBQC 的理論模型之前,這里先對量子計算中的一些關鍵概念進行說明.

量子信息處理的基本單元稱為量子比特(qubit),它可以表示為兩個狀態|0〉和|1〉的疊加態:

其中復數c0和c1稱為振幅且滿足歸一化條件,右矢(ket)|〉是表示量子態的狄拉克符號.1 個qubit 態可視為1 個二維復向量空間中的向量,而|0〉和|1〉構成此向量空間的正交基,稱為計算基態(computational basis state).對于n個qubit 構成的量子系統,其計算基態|x1x2···xn〉共有 2n個,故此系統中的任意1 個量子態都可以由2n個振幅值確定.因此,用經典計算機存儲1 個nqubit 量子態的所有振幅信息需要指數級增長的空間.實際上,量子態中往往蘊含著豐富的關聯和糾纏信息[16],其中2-qubit 糾纏態的典型例子為4 個正交Bell 態:

量子計算即為對多量子比特所構成的量子態進行一系列特定操作以達成目標結果的新型計算模式,其過程遵循量子力學規律.主要有兩類量子操作:量子門變換操作和測量操作.量子門可以表示為作用到量子態上的幺正矩陣,常用的單量子比特門如泡利算符(X,Y,Z)和Hadamard 門(H)為

單量子比特旋轉門操作為

常用的兩量子比特門有受控非(controlled-NOT,CNOT)門和受控Z(controlled-Z,CZ)門:

其上標 (a,b) 表示2-qubit 門的受控位和靶位分別為a和b.理論上[2](6)—(8)式中的單比特旋轉門和(9)式的兩比特門可以合成任意的幺正變換矩陣.

量子測量由一組作用到量子態空間的測量算符{Mm}描述,其中下標m表示測量1 個量子態|ψ〉后可能得到的結果,其發生概率為

相應地系統狀態在測量后變化為

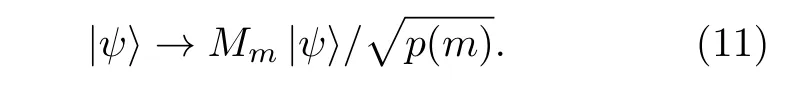
注意測量算符{Mm}需滿足完備性關系:

以確保對于任意量子態|ψ〉,(10)式所示測量態|ψ〉后得到所有可能結果的概率之和為1.

最常見的量子測量是投影測量(projective measurement)操作,由1 個可觀測量O描述.O是作用到量子態空間上的厄米算符,具有譜分解:

其中Pm為O本征空間的投影算符,m為相應本征值.測量量子態|ψ〉得到結果m的概率為

且測量后量子系統的態變化為

可以看出,當一般量子測量中符合(12)式的算符{Mm}為厄米算符,且滿足MmMm′=δm,m′Mm時,(10)式和(11)式可分別約化到(14)式和(15)式,即為執行投影測量操作.通常(13)式中的投影算符Pm可以寫為|φm〉〈φm|的形式,|φm〉稱為投影測量基.例如,以(1)式為測量基可對量子態做單比特局域測量,以(2)式和(3)式為測量基可執行量子傳態中所用Bell 測量[17,18].

在量子門電路模型中,通過排布好的量子門對輸入態執行特定幺正變換以得到目標輸出態,并可由測量操作讀取結果.下面著重介紹本文關注的對象:基于測量的量子計算模型(MBQC).

2.2 MBQC 理論模型

首先需要指出的是,所謂基于測量的量子計算并非只能執行測量操作,而是指計算的過程主要由測量操作序列來確定.大部分情況下,人們提到MBQC 默認指的就是自2001 年Raussendorf 和Briegel[3,4]提出的單向量子計算 (one-way quantum computation,1WQC)模型.但是嚴格來講,MBQC 也包含其他一些理論模型,如基于隱形傳態的量子計算(teleportation-based model of quantum computation,TQC)模型[19],基于量子態轉移的方法[20,21],關聯空間中的MBQC 模型[22,23]等.下面主要對1WQC 進行解釋,并簡要介紹TQC.

與量子電路模型通過門變換得到目標態不同,1WQC 模型的執行過程分為3 步:1)制備“普適資源態”,即系統初始制備1 個可用于普適量子計算的特定糾纏態,并劃分為S1和S2兩部分;2)依次對S1部分執行適應性單qubit 測量,即該過程中的測量操作都是作用在單qubit 上的,且后一步測量操作的設置依賴于前一步的測量結果;3)對S2中qubit 進行泡利修正,根據第2)步中測量S1的結果,對作為輸出態的S2部分執行(4)式和(5)式中的局域泡利操作X和Z,從而確定性地得到目標態[24-26].如果還需進一步讀取該輸出態的測量結果,那么泡利修正可直接吸收到對輸出態的測量操作中[3,4],此時整個計算過程就只包含對資源態的適應性測量.1WQC 最常用的普適資源態為量子簇態(cluster states)和圖態(graph states)[13,27,28],這里對二者進行簡要介紹.2001 年Briegel 和Raussendorf[27]考慮在具有伊辛類型相互作用的自旋鏈或自旋晶格中的量子比特,按特定哈密頓量進行演化得到態為

其中C為一部分量子比特形成的“簇(cluster)”,對于一維鏈、二維晶格和三維晶格分別有T={1},T={(1,0),{0,1}}和T={(1,0,0),{0,1,0},{0,0,1}},當c+t∈/C時,這樣的(16)式稱為簇態.簇態同時具有所謂的最大連通性(maximum connectedness)和糾纏持久性(persistency of entanglement),并經論證可用作1WQC 模型的資源態[3].類似地,量子簇態的定義被進一步推廣到與圖相聯系的量子圖態[4].首先考慮1 個由N個頂點的集合V={a1,a2,···,aN}和連接它們的邊的集合E構成的圖G=(V,E) .圖G的鄰接矩陣AG為1 個N×N矩陣,其元素為

并且對于1 個給定的頂點a ∈V,其近鄰頂點的集合Na ?V中的元素b滿足{a,b}∈E.

對于任意1 個圖G=(V,E),都可以定義1 個對應圖態.令每1 個頂點a ∈V對應一個qubit,考慮與之相關的1 個厄米算符:

圖態|G〉也可以根據圖的結構直接制備.首先將所有頂點處的qubit制備為疊加態|+〉=(|0〉+,然后對所有鄰接頂點{a,b}∈E上的一對qubit 執行(9)式中的幺正操作 CZ(a,b),就可得到圖態|G〉:

在大信號掩蓋下，機密信號的解調必然受到影響.下面分析機密信號解調BER(Bit Error Rate).機密信號在(i-1)Tw≤t

不同結構的圖會導致具有不同性質的圖態,見圖1,其中線性簇態和馬蹄形簇態均為圖態特例[29],星形圖態在局域幺正變換下等價于GHZ 態[30],可擴展的2D 方格圖態用于執行普適MBQC[3,28].在大多數MBQC 的相關研究中,都將簇態視為定義在特定晶格結構上的圖態例子[4,13,28,31],可按(20)式直接制備.下面介紹如何基于簇態確定性地執行任意單qubit 旋轉操作和2-qubit CNOT 門.

圖1 不同類型的圖態 (a)線性簇態;(b)星形圖態;(c)馬蹄形簇態;(d)可擴展的二維方格圖態Fig.1.Different types of graph states:(a) A linear cluster state;(b) a star-graph state;(c) a horseshoe cluster state;(d) the scalable 2D square graph state.

|ψout2〉與|ψout1〉僅相差一個整體相位因子,即圖2(b)等價實現了圖2(a).

進一步地,以上構造方法可推廣到實現任意單qubit 旋轉U=HRz(-γ)Rx(-β)Rz(-α) .將未經泡利X修正的圖2(b)中線路作為基本單元串聯3 次,其中各qubit 的測量基分別為|±α〉,|±β〉,|±γ〉并得到結果k,l,m ∈{0,1},則qubit 4 上的態為

接下來,介紹如何實現普適量子計算所需的2-qubit CNOT 門.注意圖1(b)所示圖態可視為六角晶格結構上的星形簇態[34],當在泡利X基中測量其qubit 1 和2 并分別得到結果m,n ∈{0,1},則剩余兩個qubit 3 和4 所處的輸出態為

因此,如圖2(d)所示先制備這樣的星形簇態,再對qubit 1 和2 做泡利X測量并對作為輸出態的qubit 3 和4 做相應泡利修正,可確定性實現|ψout4〉=CNOT|+〉|+〉.更一般地,可驗證當圖2(d)中的輸入qubit 3 和2 換成任意2-qubit態|ψin〉時,則經過后續操作最終qubit 3 和4 所處輸出態為|ψout4〉=CNOT|ψin〉.類似地,測量圖1(c)中馬蹄形簇態的qubit 1 和4 并對qubit 2 和3 做泡利修正,可以實現2-qubit CZ 門[29].以上理論顯示一般的輸入態本身也可以由測量簇態來得到,因此當如圖1(d)所示2D 方格圖態足夠大時,通過精心設計測量模式并輔以適當的泡利修正就能夠確定性地實現普適量子計算[3].若量子方案需要對輸出態做讀取測量,那么泡利修正操作也可以合并到測量操作中[4].相比于1WQC 使用單比特測量來完成計算,下面簡要介紹另一種使用兩比特測量的MBQC 模型—基于傳態的量子計算(TQC).

1999 年Gottesman 和Chuang[19]提出使用量子傳態技巧[17,18]和單qubit 操作來實現普適量子計算.圖3(a)為量子傳態的1 個例子:Alice 對制備好的單qubit 態U|α〉和(2)式中Bell 態|β00〉的1 個qubit 執行聯合Bell 測量,并將測量結果a和b發送給Bob.后者對|β00〉態的另1 個qubit 執行ZbXa,即可得到態U|α〉.實際上Alice 的操作等價于在一組新基為(2)式和(3)式中的Bell 態)中對態|α〉和|β00〉的1 個qubit做2-qubit 測量[35],則此時對U的實現只用到聯合測量操作和泡利修正.

圖3 基于傳態的方案實現單量子比特門 (a)一方遠程制備態 U|α〉并通過Bell 測量和泡利修正傳給另一方,注意U 和Bell 測量可以直接合并成新的聯合測量;(b)利用制備好的資源態 (I ?U)|β00〉來間接執行U|α〉Fig.3.Teleportation-based scheme for implementing any sing-qubit gate:(a) State U|α〉 is remotely prepared at one site and teleported to another site via Bell measurement and Pauli corrections,note here U and Bell measurement can be directly combined into a new joint measurement;(b) the scheme to indirectly implement U|α〉 via a prepared resource state (I ?U)|β00〉 .

另一種間接執行U的方式如圖3(b)所示,將態|α〉和資源態 (I ?U)|β00〉中的1 個qubit 做Bell測量,并根據測量結果對另1 個qubit 做修正操作=UXU?和=UZU?,即可確定性地得到目標輸出態U|α〉.這樣的傳態技巧可以從單量子比特門U推廣到多量子比特門的作用,如用CNOT 門作用2-qubit 態等價于制備資源態(I(1)?CNOT(3,2)?I(4))|β00〉|β00〉并執行兩組Bell 測量和相應泡利修正[19].因此,這種利用傳態思想的計算方法的好處在于:即便目標操作U難以直接實現,也可以通過制備已知的初始資源態來間接地執行U.在Gottesman-Chuang 方案的啟發下,后又發展出各種不同的TQC 模型,如Leung[35]提出對任意雙量子比特執行適應性2-qubit 測量來完成計算.

2.3 MBQC 的計算普適性及其經典模擬

在1WQC 模型中,對2D 方格簇態執行特定模式的單qubit 測量就可以實現普適量子計算.反過來1 個自然的問題是:用于MBQC 的普適資源態具有何種必要屬性? 更確切地,既然涉及有限糾纏的系統可以被經典計算機有效模擬[41],那么執行普適MBQC 的資源態中需要多少糾纏? 最強的“普適性”可以自然地定義為對資源態執行單qubit操作來產生任意量子態的能力,則此意義下的普適資源態(如2D 簇態)的多種糾纏度量必然隨系統尺寸呈現無界增長.例如,2006 年Nest 等[32]引入熵糾纏寬度(entropic entanglement width)作為評判圖態普適性的標準,并舉出對應六角晶格、三角晶格、Kagome 晶格的普適資源圖態例子.相對地,他們也揭示出n粒子1D 簇態,GHZ 態,W 態以及某些1D 自旋系統的基態至少不滿足一種糾纏度量下的最大糾纏性,因此非普適資源[25].當普適性的概念為只要求MBQC 能夠有效再現量子門電路的經典輸出結果時,矩陣乘積態(matrixproduct state,MPS)和投影糾纏對態(projected entangled pair state,PEPS)可以作為相應關聯空間量子計算的普適資源[22,23],而無需具備2D 簇態呈現的一些糾纏特征(如最大局域糾纏).

檢驗一種特定MBQC 模型計算能力的常用手段是考察其經典模擬方法:若目標MBQC 模型存在以多項式時間實現的有效經典模擬,則意味著該模型不具備加速計算的能力.在某些圖態(如1D簇態和GHZ 態)上執行的1WQC 可以用經典計算機有效模擬[32,42,43].細致考慮圖的拓撲結構和糾纏性質,研究者揭示出一系列特定資源態參與的MBQC 可以用張量網絡方法有效模擬,如任意兩體劃分的糾纏(Schmidt 數)較小[44]或具有對數有界的Schmidt-rank 寬度情形[45],有限寬度的簇態計算[46],以及圖的樹寬度較小且最大度(degree)為常數的圖態計算[42]等.除了圖態外,參考平面圖Ising 模型的嚴格可解性,基于環面碼(toric code)態這種量子資源的MBQC 也可以有效經典模擬[47].這些圍繞經典模擬的研究不僅有助于深入理解MBQC 計算能力的普適性,還能啟發新的經典算法[48,49].

2.4 MBQC 在量子信息領域的應用

MBQC 在量子信息處理領域具有多方面應用.首先,作為一種普適量子計算模型,MBQC 模型已用于構建量子Toffoli 門[7],演示Deutsch-Jozsa,Bernstein-Vazirani 算法[8,9]以及Grover 量子搜索算法[5,29,50],執行QFT[13,28]和量子加法器[4],求解Simon 問題[10],計算非線性布爾函數[51,52]等量子算法相關場景.值得一提的是,1WQC 和量子電路模型在執行這些算法上是多項式時間等價的,但前者可能在并行化方面優于后者[53,54].例如,2010 年Browne 等[55]提出QFT 在1WQC 模型中能以常數深度近似執行,從而更有利于實驗演示.因此,利用量子電路模型與MBQC 模型之間的轉換關系來研究電路的深度復雜性具有理論和實用意義.

其次,相比于使用量子糾錯碼的量子電路模型,MBQC 也為實現容錯通用量子計算提供了新的途徑.早在2003 年,Raussendorf[56]就討論了容錯1WQC 方案:可使用2D 簇態模擬1D 容錯量子電路.隨后,Nielsen 和Dawson[57]也證明了當錯誤率低于某個閾值時,能夠實現基于簇態的可擴展容錯1WQC,并以光學量子計算中的光子損失噪聲和去極化噪聲為例數值研究了容錯閾值[58].Raussendorf 等[59,60]還進一步利用3D 簇態中的2D 切片來模擬一種常用的糾錯碼—表面碼(surface code),其中特定的測量模式可模仿拓撲量子計算中的任意子編織操作.這樣以拓撲保護的量子門實現的容錯MBQC 具有較高的容錯閾值[61,62],且適合qubit 和連續變量系統的實驗演示[63-65].

最后,MBQC 的理念還能運用到網絡編碼[12]、盲量子計算[66,67]、多人協作量子計算[68]、量子博弈[69]、量子通信[70]等量子信息處理場景中.例如,量子網絡編碼技術有望提升分布式量子計算中的資源利用率,而使用量子簇態實施糾纏交換(entanglement swapping)或基于測量的糾纏分布(entanglement distribution)時可以給電路深度[71]、最終的Bell 態保真度[12]等方面帶來改善.又如盲量子計算是一種與MBQC 模型有緊密聯系的安全計算協議.未來量子計算機可能趨向于以云計算形式提供給客戶使用,因此如何保證客戶的數據和計算過程的私密性顯得尤為重要.2009 年Broadbent等[66]首次提出的通用盲量子計算協議中,客戶端將制備好的隨機量子比特發送給服務器,服務器將這些qubit 制備為brickwork 糾纏態并按客戶的要求進行測量,再將測量結果返回給客戶端,后者又根據這些測量結果確定后面量子比特的測量參數并發送給服務器.這樣雙方不斷交互進行直至所有量子比特都被測量,協議完成.此協議秉承MBQC的基本思想,能夠保證客戶端的信息安全.在物理學領域,MBQC 模型可以用作研究經典自旋模型[72,73]、量子模擬架構[74]及對稱保護的拓撲相[75]等物理理論的工具.

3 MBQC 的物理內涵

特定MBQC 模型的計算能力與其內在的物理屬性有緊密聯系,如一類利用量子關聯及非適應性測量的計算模型可展現出相對經典局域隱變量模型的量子優勢[76].下面從量子糾纏、量子關聯、對稱保護的拓撲相等角度概述相關物理內涵.

3.1 MBQC 中的量子糾纏

MBQC 模型的計算能力可以追溯到其所用糾纏資源態的性質.在2.3 節中,已概述了糾纏和MBQC 的普適資源態及經典可模擬性之間的關系.后續圍繞量子糾纏在MBQC 中作用的研究包括:一些多體糾纏量子系統的基態(如自旋 5/2 系統[77]和自旋 3/2 系統[78])可用作普適MBQC 的資源態,而某些具有兩體相互作用的自旋 1/2 無阻挫哈密爾頓(frustration-free Hamiltonian)系統則無此能力[79];關聯空間中執行“普適態制備”意義下的MBQC 時,所用資源必然會展現類似簇態的極值糾纏特征[80];近年類比量子圖態提出的超圖態[81,82],其獨特的糾纏和非局域性質導致相應MBQC 在一些方面優于圖態方案,例如2016 年Gachechiladze等[83]揭示出超圖態相比于GHZ 態對于粒子損失噪聲具有更強的魯棒性.

有趣的是,2009 年Gross 等[84]發現隨機態等具有過多糾纏的量子態反而無益于MBQC 展現量子計算加速.同年,Bremner 等[85]也在抽象MBQC框架下得到了類似的結果.實際上,2017 年Morimae[86]論證了尋找適用于MBQC 的資源態通常是1 個困難任務.

3.2 MBQC 模型與量子關聯

量子關聯是量子計算、量子通信等領域的重要資源,其具體表現如量子非局域性(quantum nonlocality)[87]和量子互文性(quantum contextuality)[88]可用于分析和詮釋MBQC 中通過測量糾纏資源態展現的計算能力.

2009 年,Anders 和Browne 通過定義1 個一般性的框架分析“關聯的計算能力”[89],并以典型的GHZ 和CHSH 問題作為例子,揭示出局域實在模型的違背和糾纏資源態的計算能力之間的有趣關系,例如3-qubit GHZ 態加上線性副處理(經典異或門和非門)足以實現經典計算所用的普適與非門.如圖4 所示,此計算模型包含兩部分:1 個關聯多方資源態和1 個經典控制計算機,彼此之間可以交換經典信息.其中關聯多方資源由一些個體組成,控制計算機可為其提供k個不同的測量設置,每個個體經測量后得到l個可能結果中的1 個并返回控制計算機.當設置k=l=2 時,此框架與原始的量子one-way 模型相符.此外,他們還從計算復雜度的角度探討了在使用不同的資源態(如簇態,二維圖態,計算張量網絡態等)和僅包含經典CNOT 操作和NOT 操作的計算機時,三種復雜度類別⊕L,P和BQP之間可能的轉化關系.除了直接考察量子資源態中的關聯,2014 年Hoban 等[90]提出利用量子方式生成的概率分布中的關聯,來構造一種MBQC 的經典對應(稱為“基于測量的經典計算”,MBCC),可以展現特定量子模型的非經典計算特性,如計算一種可能無法用傳統經典計算設備有效模擬的IQP*量子線路.

圖4 利用關聯的計算模型.經典控制計算機提供k 個測量設置中的1 個作為對關聯多方資源態中個體的經典輸入(藍色箭頭),并且接收l 個測量結果中的1 個(紅色箭頭)作為輸出Fig.4.A computational model exploiting correlations.The classical control computer provides one of k measurement settings as the classical input (blue arrows) to each of the parties in the correlated resource state and receives one of l possible measurement results (red arrows) as the output.

與具有適應性測量的MBQC 模型相比,2011年,Hoban 等[91]提出在一般的具有線性副處理(做模2 加法運算)且非自適應的MBQC (non-adaptive MBQC with linear side-processing,NMQC⊕)模型,通過測量特定糾纏態得到的非局域關聯結果可以實現對非線性布爾函數的確定性計算、與多方Bell 不等式違背有關的概率計算等.2013 年,Raussendorf[51]展示了在一些自然的假設下,以高成功率計算1 個非線性布爾函數的MBQC 具有互文性.互文MBQC 中的1 個有趣例子是求解離散對數問題的量子算法,其相對經典算法能展現超多項式加速.2017 年,Oestereich 和Galv?o[52]進一步基于互文性MBQC 發展出的非線性函數計算模型中,實現了可靠計算所需的3-MAJ 門和3 輸入的XNAND 門.與僅能計算線性布爾函數的局域隱變量模型或非互文隱變量模型相比,NMQC⊕模型僅用少量量子資源就能展現量子優勢,且2017年Abramsky 等[92]提出一種互文性度量方式來量化這樣的量子優勢.這是不同于某些量子霸權方案中通過不斷擴展量子規模來達到量子優勢的思路[93],為人們理解量子計算與經典計算之間的差異提供新穎的視角.此外,由于不需要用到傳統適應性測量操作,NMQC⊕模型對實驗維持相干性的要求更低,因而更容易在近期的實驗平臺上進行演示.2021 年,Demirel 等[76]于實驗上演示了利用4 光子GHZ 態來計算簡單的低度非線性函數.

3.3 MBQC 與對稱保護的拓撲相

具有特定群對稱性的量子態所呈現的多體糾纏可導致所謂的對稱保護拓撲序(symmetry-protected topological order,SPTO)現象[94-97],而SPT態可以為MBQC 普適資源態的刻畫提供一種新的視角.2012 年,Else 等[98]論證了所有屬于1D 自旋鏈SPT 相的基態都具有“量子計算導線(quantum computational wires)”的統一屬性,如Z2×Z2旋轉對稱性保護的1D 簇態和1D Affleck-Kennedy-Lieb-Tasaki (AKLT)態,并能確保MBQC 中恒等門的完美操作.2015 年,Miller 和Miyake[99]展示了S4對稱下的1D SPT 相能以任意高保真度執行單qubit 門操作且能作為TQC 的潛在資源,隨后2017 年Raussendorf 等[100]將該結果推廣到了執行更一般的MBQC 模型.

在1D 物質相研究的基礎上,2015 年Nautrup和Wei[101]刻畫了任意晶格上的元格態(plaquette state)呈現的非平凡SPTO,及用作MBQC 的普適資源態.與之不同的是,2016 年Miller 和Miyake[75]提出將3-qubit CCZ 門作用到位于Union Jack 晶格中三角元胞上的qubit,可以得到具有2D SPTO的資源態(系統具有Z2×Z2×Z2對稱).該工作指出具有1D SPTO 的糾纏態(如傳統簇態)配合任意單qubit 測量可以實現普適量子計算,而對于具有更加復雜糾纏形式的2D SPTO 只需執行泡利測量就可以得到相同的結果.基于Union Jack 態實現普適MBQC的工作將凝聚態物理中SPTO 的層級概念和量子計算中的所謂Clifford 層級聯系起來.這樣的量子計算普適性也于2018 年推廣到了d維量子比特(qudit)系統的非平凡Zd×Zd×ZdSPT 態[102].除了以上運用群上同調(group cohomology)工具構建MBQC 的普適資源態及SPTO分類,最近一兩年的工作系統性地研究所謂“量子物質的計算相(computational phases of quantum matter)”概念,指出具有普適計算能力的對稱保護量子相由所謂的子系統對稱性保護[103-105].在取得這些理論成果的同時,2018 年以來對SPT 態的表征和基于測量的算法也出現實驗演示[106,107].

4 MBQC 的實驗進展

除了理論進展外,在硬件方面當前量子技術已進入NISQ 時代,光量子、離子阱、超導體系、半導體量子點等多條技術路線并行發展,面向特定領域、特定問題的專用量子計算設備已取得了較大進步.下面概述量子實驗中對于MBQC 算法的演示或相關量子原理的驗證.

4.1 光量子系統

光子具有能同時應用于量子信息處理的多自由度(極化、軌道角動量、空間模式、頻率等)和退相干率低等特點,近年來研究者圍繞MBQC 計算模型開展了一系列基于光學系統的實驗演示,主要包括以下幾方面:

2005 年Walther 等[29]利用后選擇技術制備4 光子簇態并實現1WQC 中的基本要素:單量子比特旋轉門和兩量子比特受控門,并演示四元素搜索的Grover 算法.隨后的光學實驗擴展到利用多光子多自由度制備糾纏圖態,且運用前饋技術來克服執行測量操作時的隨機誤差,從而執行確定性1WQC 中的門操作[5,34,50,108,109],并演示Deutsch算法[8,110]和Simon 算法[10],量子博弈[69],盲量子計算[67],量子糾錯碼[111],關聯空間中的MBQC 模型[112]等.2019 年,Reimer 等[113]利用光子的時間和頻率自由度實驗演示了基于多能級簇態的高維1WQC,顯示出相對傳統二能級簇態更高的抗噪特性.從技術上看,1WQC 模型與集成光量子芯片技術的結合有助于未來可擴展的光學量子信息處理[114,115].

在基于傳態的計算模型方面,以Gottesman-Chuang 傳態計算理論[19]為基礎,2001 年Knill-Laflamme-Milburn (KLM) 方案[116]僅用分束器、相移器、單光子源和光探測器等構成的線性光學系統就能有效實現量子計算.具體而言,光探測過程中潛在的非線性可以通過測量轉移到量子比特上,從而實現普適計算.2005 年,中國科學技術大學郭光燦課題組[117]利用線性光學操控、參數下轉換產生的光子極化-路徑糾纏以及符合測量中的后選擇技術,實現了TQC 模型中關鍵的量子CNOT門傳輸.隨后,該組又實現了傳輸單量子比特旋轉作用于遠程光子[118].2010 年,潘建偉課題組[119]也發展出了基于其他光子自由度和糾纏態來實現傳輸量子門的實驗方案及演示工作.

除了離散變量系統,近年來MBQC 也在多模連續變量光學系統中得以實現.山西大學彭堃墀課題組[120-123]和東京大學Furusawa 課題組[65,124-126]在制備連續變量光學簇態和實驗演示MBQC 方面積累了顯著的系統性工作,當前基于連續變量系統執行容錯MBQC 的挑戰在于低錯誤率立方相位門的實現及可擴展的光學集成等方面.

4.2 離子阱體系

早在1995 年Cirac 和Zoller[127]就提出了將離子阱系統用于量子計算的方案.離子阱將一串離子囚禁在線性阱中,且用其冷卻到基態的兩個內能級編碼1 個量子比特.單比特操作可以通過激光脈沖尋址作用在相應離子上實現,兩比特的受控操作可通過用離子串的公共質心及聲子協助完成,測量離子發出的熒光光譜就實現了量子態讀取.離子阱系統在制備二維簇態上表現出良好的擴展性[128],且可在2D 離子阱陣列上演示適用于容錯MBQC 方案的3D 簇態[129].2013 年Lanyon 等[6]制備多種不同類別的圖態用于演示MBQC 中的普適門操作和糾錯碼,并獲得較高的態保真度.進一步地,該課題組[130]也演示了離子阱系統圖態對于多方Bell不等式的違背.

4.3 超導量子體系

在超導量子系統中,基于約瑟夫森效應構造超導約瑟夫森結作為量子比特,通過施加電流、電場或微波控制實現相應的量子門操作.早期MBQC相關的實驗方案包括:超導量子電路中使用“一步法”制備大規模簇態[131],與腔QED 相結合的超導量子比特系統[132-134]等.2019 年,潘建偉組在超導電路系統制備具有真多方糾纏且保真度達到70%的12 量子比特簇態[135],Mooney 等[136]也基于IBM的量子云平臺制備20 量子比特規模的圖態并用特定的糾纏見證(entanglement witness)進行刻畫,且Albarrán-Arriagada 等[137]提出使用幾十個量子比特執行1WQC 且相比簇態更加節省資源的超導實驗方案.這些成果為未來可擴展的MBQC 奠定了理論和實驗基礎.目前已有一些基于超導電路的量子計算云平臺問世(如IBM Q),方便研究者們實驗演示各種MBQC 相關的信息處理方案,如執行基于測量的量子網絡編碼[12].

4.4 其他方案

當前,基于其他物理體系來制備量子簇態和圖態或演示MBQC 模型的方案包括光學晶格囚禁冷原子體系[138,139]、量子點[140,141]、核磁共振(NMR)系統[142]、腔量子電動力學(QED)[143]等.整體而言,當前基于離散變量系統演示MBQC 的實驗規模還局限在幾十個量子比特,而連續變量系統技術上可以產生具有上百萬個不可分模式的簇態[126].這些實驗技術與方法的新進展為未來實現大規模MBQC 提供了更多選擇.

5 MBQC 的未來研究展望

如前文所述,MBQC 將量子信息處理和凝聚態物理領域中的問題相聯系,相關研究內容至今還在不斷拓展和深化.這里對未來具有潛力的研究方向進行討論和展望.

1)構建基于新型資源態的MBQC 模型.例如在實現普適計算方面,對一類具有對稱保護拓撲序的Union Jack 態執行單qubit 泡利X,Y和Z測量[75],或對2019 年Takeuchi 等[144]構造的特定超圖態僅用泡利X和Z測量都足以實現普適量子計算.就計算魯棒性而言,超圖態本身的一些非局域性和糾纏性質使得其對于局域實在(local realism)呈現指數增加的違背,因而可以很好地抵抗粒子損失[83].如何基于其他類別的資源態設計抗噪且操作簡便的普適MBQC 也符合實際的實驗需求.此外,2019 年Gachechiladze 等[145]提出了一種3-一致超圖態用作新型確定性MBQC 的資源態,且相關計算模型具有一些新的特征:僅用泡利測量就可以實現普適計算;允許并行執行所有的邏輯CCZ和SWAP 門;計算的邏輯深度等于邏輯Hadamard門的整體層數等.因此,有望進一步從深度復雜性和并行化計算的角度研究MBQC 的優化方案.

2)量子關聯與特定計算模型之間的關系及其應用.在3.2 節中已介紹了MBQC 模型和量子關聯非經典性之間的緊密聯系,這些研究近年來啟發了不少新奇的后續進展,如2018 年Mansfield 和Kashefi[146]提出“序列文本變換中的互文性”可能導致的計算優勢,Frembs 等[147]展示在d維qudit系統中,強非局域性配合經典線性處理足以估計高度多項式函數.因此,值得進一步探索的問題是:其他類型的MBQC 是否也具有特定的量子關聯特性? 這樣的特性能否帶來相對經典算法的計算優勢? 傅里葉分析理論表明任意的布爾函數都具有相應的多項式表示.因此,進一步發展和挖掘NMQC⊕以及MBQC 模型的潛力,有望構建出能計算任意非線性布爾函數且相對特定經典模型展現量子優勢的新型計算模型,并應用到依賴于Bent 函數等高度非線性布爾函數的密碼學[148],或需要非線性激活層的量子神經網絡[149]等領域.不同量子資源態在計算特定布爾函數的同時,所得結果又能反過來用于測試和核實該量子態在實際實驗中的非經典特性,預示著新的量子態驗證方法.

3)用于普適量子計算的物質相研究.從凝聚態物質的角度看,量子計算的物質相是1 個有趣的交叉研究方向[103,104].如3.3 節所述,考慮SPTO的概念包含了多種不同類別的態結構和物質相,進一步探索SPTO 和MBQC 及量子元胞自動機(cellular automaton)這幾者之間的關系,有助于構造新型計算普適的物質相(如對稱保護簇相[105,150]),及相應SPT 態執行普適量子計算的具體例子.在應用層面,考慮將MBQC 和拓撲糾錯的思想結合起來,能促進對噪聲環境中順利運行的可擴展量子計算設備的研制.

6 總結

MBQC 計算模型及相關理論經過近二十年的發展其內涵已得到了極大豐富,重要結果和相關文獻資料繁多,本文在選題上注重基礎概念和典型案例,希望能啟發讀者進一步學習和探索本文中未加詳述但同樣具有重要研究意義的相關課題,如用于普適MBQC 的AKLT 態[151],MBQC 與經典自旋模型的聯系[72]等.本文涵蓋的主要內容如下.

首先,簡要介紹MBQC 模型的基礎概念和基本原理,包括用作計算資源態的量子圖態,典型1WQC 和TQC 模型的執行過程,MBQC 模型用于普適量子計算的條件及其在量子信息處理領域的應用.接著,分析了MBQC 的計算能力和多體物理系統之間的聯系.前人的研究從多角度揭示出多體系統的各種量子特性,如量子糾纏、互文性、量子非局域性、對稱保護的拓撲序等是MBQC 模型能展現特定計算能力的物理根源.這些發現既可以促進MBQC 等相關新型量子計算模型的設計和原理分析,也為復雜量子系統的性質研究提供了來自計算機科學領域的審視.然后梳理了演示MBQC的不同技術路線,包括光量子、離子阱、超導電路等多種方案的實驗進展.最后展望未來MBQC 模型的潛在研究方向,除了用于MBQC 的資源態類型和物理性質可進一步豐富和擴展外,還能與計算機領域關心的核心問題相聯系,從而應用到更廣闊的信息處理場景.

總之,MBQC 以具有不同糾纏特性的量子多體系統為資源態,將其特有的非局域性、互文性和拓撲保護等物理性質與進行信息處理的卓越能力(如量子優勢)相聯系,為實現普適量子計算或特定算法提供了新的理論途徑,且相關實驗演示促使人們不斷提升對于量子物理系統的構建與操控水平.因此,圍繞MBQC 模型開展的研究將會給量子物理學、計算機科學、光學和材料學等多個學科領域帶來新的啟示,并促進NISQ 時代下量子計算機的發展.