巧用點子圖建構(gòu)乘法計算模型，為學(xué)生的思維搭橋鋪路

宋霞林

摘要：點子圖是小學(xué)計算教學(xué)中常見的數(shù)學(xué)模型，特別在乘法計算學(xué)習(xí)中，教科書借助點子圖這一直觀教學(xué)模型，引導(dǎo)學(xué)生建構(gòu)兩位數(shù)乘一位數(shù)、兩位數(shù)乘兩位數(shù)的豎式計算過程，數(shù)形結(jié)合，讓學(xué)生直觀理解乘法豎式筆算的算理與算法。

關(guān)鍵詞：小學(xué)數(shù)學(xué);點子圖;乘法計算

中圖分類號：A ?文獻(xiàn)標(biāo)識碼：A ?文章編號：（2021）-41-297

《小學(xué)數(shù)學(xué)課程標(biāo)準(zhǔn)》 明確指出：在數(shù)學(xué)課程中，應(yīng)當(dāng)注重發(fā)展學(xué)生的數(shù)感、符號意識、空間觀念、幾何直觀、數(shù)據(jù)分析觀念、運(yùn)算能力、推理能力和模型思想。點子圖作為一種幾何直觀的形式引入到兩位數(shù)乘兩位數(shù)筆算乘法中， 發(fā)揮著不可或缺的重要作用： 一方面， 點子圖幫助學(xué)生直觀地明晰乘法計算的算理， 使不易理解的算理變得簡明、形象、可視化;另一方面， 借助點子圖促使學(xué)生在操作活動中自主建構(gòu)乘法的口算模型， 讓算理有章可循，有理可說。 下面以北師大版教材為例結(jié)合小學(xué)三年級兩位數(shù)乘一位數(shù)和兩位數(shù)乘兩位數(shù)的教學(xué)實踐談?wù)匋c子圖對學(xué)生模型建構(gòu)及思維發(fā)展的影響。

一、數(shù)形結(jié)合，有效的輔助學(xué)生理解算理算法

在三年級上冊“螞蟻做操”教學(xué)中，學(xué)生第一次學(xué)習(xí)乘法的豎式計算，受加減法豎式的影響，部分學(xué)生會出現(xiàn)兩位數(shù)乘一位數(shù)只乘個位上的數(shù)作為乘積的錯誤，如果教師在計算教學(xué)中只是一味強(qiáng)調(diào)乘的過程要完整，對于這類錯誤并不見效。追根究底，學(xué)生對乘法的計算算理并不理解，如果借助直觀的點子圖，要求學(xué)生在點子圖上圈一圈，算一算，學(xué)生便能清楚地知道12×4中2×4是求出兩列有多少個點，10×4是求10列有多少個點，合在一起共48個點。在《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》中指出：“幾何直觀主要是指利用圖形描述問題和分析問題。借助幾何直觀可以把復(fù)雜的數(shù)學(xué)問題變得簡明、形象、有助于套索解決問題的思路，預(yù)測結(jié)果。”學(xué)生通過直觀地圖形找到了計算的算理，對于學(xué)生來說，這樣點子圖直觀生動、易于理解、印象深刻。為學(xué)生接下來的兩位數(shù)乘兩位數(shù)的筆算算法奠定基礎(chǔ)。

二、幫助學(xué)生溝通不同形式的內(nèi)在聯(lián)系，促進(jìn)深入學(xué)習(xí)

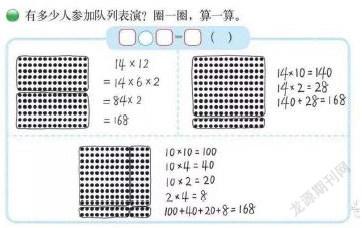
在三年級下冊“列隊表演（一）”教學(xué)中，教材創(chuàng)設(shè)了學(xué)校舉行隊列表演情景（一共有12行，每行有14人）。在解決有多少人參加隊列表演時，多數(shù)學(xué)生根據(jù)以往乘法學(xué)習(xí)經(jīng)驗，已經(jīng)會用橫式來完成計算，如：14×2=28， 14×10=140，140+28=168。少部分學(xué)生會用乘法豎式表示計算過程，也出現(xiàn)了步驟不完整或者是數(shù)字占錯位的問題，這些問題都暴露了學(xué)生對兩位數(shù)乘兩位數(shù)乘法的算理不理解，計算模型是不清晰。教材中再次出現(xiàn)的點子圖巧妙的將乘法豎式計算的步驟與對應(yīng)的點子聯(lián)系起來，通過直觀的觀察，讓學(xué)生明確了乘法豎式的計算方法與橫式計算、點子圖有著內(nèi)在的聯(lián)系，例如在課堂教學(xué)中教師通過“連一連，找一找，看一看，說一說”活動環(huán)節(jié)的設(shè)計讓學(xué)生發(fā)現(xiàn)豎式、橫式、點子圖雖然形式不同但都是用同種方法計算14×12，有利于學(xué)生發(fā)現(xiàn)豎式和橫式之間的對應(yīng)關(guān)系， 發(fā)掘出算理和算法之間的聯(lián)系與共同之處，發(fā)現(xiàn)所有算法都在“拆分”， “拆分”的目的是為了轉(zhuǎn)化，自然而然地在學(xué)生心中建構(gòu)乘法豎式計算的模型，也促進(jìn)學(xué)生思維從直觀到抽象，從片面到整體的發(fā)展。

三、豐富學(xué)習(xí)經(jīng)驗，幫助學(xué)生形成多樣化的算法

還是在“列隊表演（一）” 中，教材出示了三種點子圖的圈法：①把12行分成6行和6行;②把12行分成10行和2行;③ 分成大小不同的4部分。這三種不同圈法對應(yīng)三種不同的拆分計算，前兩種方法對學(xué)生后續(xù)學(xué)習(xí)乘法結(jié)合律、分配律有著重要的啟示，第三種方法還可以看到多項式乘多項式的雛形，為學(xué)生做了長遠(yuǎn)的鋪墊。由于點子圖方便操作，通過在圖上分一分、圈一圈能清晰直觀地表示出不同算法，很好地激發(fā)學(xué)生嘗試和操作的欲望，這也有利于學(xué)生思維的發(fā)散，探索出不同的計算方法。

總而言之，點子圖作為小學(xué)乘法計算數(shù)學(xué)教學(xué)中的典型直觀模型，在小學(xué)數(shù)學(xué)的教學(xué)中發(fā)揮著不可替代的作用，但是當(dāng)學(xué)生慢慢形成口算兩位數(shù)乘兩位數(shù)的數(shù)學(xué)思維和學(xué)習(xí)經(jīng)驗的時候，也會慢慢丟下點子圖，然后形成自己的口算能力。點子圖能夠為學(xué)生的思維搭橋鋪路。學(xué)生充分利用點子圖， 挖掘口算的算理，建立口算和豎式之間的內(nèi)在聯(lián)系。教學(xué)中點子圖這種直觀的教學(xué)工具在幫助孩子經(jīng)歷從算式到具象的過程中的價值是不可否認(rèn)的。但是，當(dāng)算理借助點子圖在學(xué)生心中悄然開花之后， 最終還是要走向計算方法。學(xué)生總有一天要學(xué)會丟掉點子圖這根直觀的“拐杖”內(nèi)化形成為自己的算理和算法。

參考文獻(xiàn)

[1]吳斯嫻.從學(xué)生的需要出發(fā)用好“點子圖”——“兩位數(shù)乘兩位數(shù)的筆算乘法”三次教學(xué)實踐與反思（J）.小學(xué)數(shù)學(xué)教育.2015.17

[2]鄧德彬. “點子圖”——促進(jìn)數(shù)學(xué)理解的有功之臣（J）.新世紀(jì)小學(xué)數(shù)學(xué)，2015.5

[3]黃慧章.幾何直觀——讓算理看得見，讓算法說得清（J）. 小學(xué)數(shù)學(xué)2017.9