一種新的魯棒PM濾波及其在組合導航中的應用*

梁 浩 張子劍 賈 睿 崔利軍

1.北京宇航系統工程研究所，北京 100076 2.太原衛星發射中心，山西太原 030027

0 引言

星光導航系統(CNS)具有精度高、自主隱蔽的特點，能夠為載體提供高精度姿態信息[1]；合成孔徑雷達(Synthetic Aperture Radar，SAR)是一種高精度微波成像雷達，它具有全天時、全天候、遠距離工作的優點[2]；CNS、SAR和捷聯慣導(SINS)組成的CNS/SAR/SINS組合導航系統是一種性能優異的無依托自主導航方式[3-4]。

Kalman濾波限制條件比較苛刻，要求系統模型精確已知，然而在實際應用中，受各種條件的限制，很難獲得噪聲準確的先驗統計特性；另一方面，系統的噪聲特性也是不穩定的，噪聲特性因內部器件特性變化或外部力學沖擊等環境因素，可能產生不可預知的變化。

為了處理這種存在偏差的系統，魯棒濾波被研究并發展應用起來，M估計濾波和H∞濾波是2種最典型的魯棒濾波，被廣泛用來處理高斯分布受到污染或干擾的系統。M估計濾波對應用系統的噪聲特性變化較遲鈍，能夠解決系統噪聲和測量噪聲統計特性不確定的問題[5-6]，H∞估計濾波將模型誤差看作未知但有界的噪聲，使噪聲污染情況下的估計誤差最小[7]，但當系統出現尖銳的野值時，M估計濾波和H∞濾波均會出現較大誤差以至發散。

本文針對組合導航系統中出現多種尖銳野值的情況，引入GM估計野值檢測抑制方法，構建了魯棒PM估計濾波，應用于高空飛行器CNS/SAR/SINS組合導航中，并進行了仿真分析。

1 基于M估計的線性濾波

1964年，Huber經過嚴格的推導[5]，提出了廣義極大似然估計，即M估計魯棒濾波。針對高斯噪聲受到污染的系統，M估計結合了l1和l2范數構造代價函數，其魯棒性優于l2范數估計，其優點是保證最大漸近估計方差最小以及純高斯分布時l2范數估計的效率。

線性離散系統如下

xk=Fk-1xk-1+wk-1

(1)

yk=Hkxk+vk

(2)

式中：xk為狀態量，yk為觀測量，Fk-1為狀態轉移矩陣；系統噪聲wk-1和量測噪聲vk為高斯白噪聲，方差為Qk-1和Rk。

1)預測

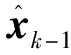
(3)

(4)

2)更新

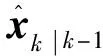
(5)

針對量測更新過程，構造線性回歸模型以提高系統的冗余性：

(6)

定義如下變量：

(7)

(8)

(9)

(10)

則線性回歸模型可以轉化為

zk=Mkxk+ξk

(11)

M估計求解如下代價函數的極小值，通過求解代價函數獲得狀態估計值：

(12)

式中：ei=(zk-Mkxk)i；ρ為任意函數，通過選擇ρ函數，可以使估計器獲得某些特定的性質，Huber建議的ρ函數形式如下

(13)

式中：μ為可調節參數。而當殘差較大時，ρ函數具有l1范數的性質，相反當殘差較小時，ρ函數具有l2范數的性質。通過配置μ，可以使濾波器在高斯分布下具有較高的估計效率，并且能夠抑制濾波噪聲污染對系統的影響。

Huber在公開文獻中已證明，當選擇式(13)作為ρ函數的形式時，M估計濾波對受污染的高斯系統具有漸近最優魯棒性。

2 魯棒PM估計

2.1 系統野值的類別及影響

在實際系統中除了存在受污染的高斯噪聲，還會存在各種干擾野值，一般認為在組合導航系統中出現的野值主要是系統狀態野值和量測野值2種，然而狀態轉移矩陣和量測矩陣中也會出現野值，稱為結構野值，結構野值是由時變系統模型匹配錯誤和計算浮點數錯誤等引起的，3種類型野值列表如下。

在回歸模型中野值點遠離其它正常點，會對M估計產生較大的影響，M估計也僅能夠抑制系統的部分量測野值，當系統同時存在表1中的3種野值時，M估計濾波會出現偏差。

表1 組合導航系統中3種野值類型

近年來，在電力系統狀態估計中，出現了一種廣義M估計(GM估計)濾波算法[8]，通過構造回歸模型并采用迭代方法求解最優估計，GM估計對量測野值、狀態野值和結構野值均具有魯棒性。GM估計包括Mallows型GM估計和Schweppe型GM估計2種，Mallows型GM估計在目標函數中引入權函數以降低所有量測點的權重，Schweppe型GM估計只針對野值點進行衰減，后者具有更高的效率。

2.2 GM估計中的PS野值檢測方法

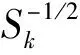
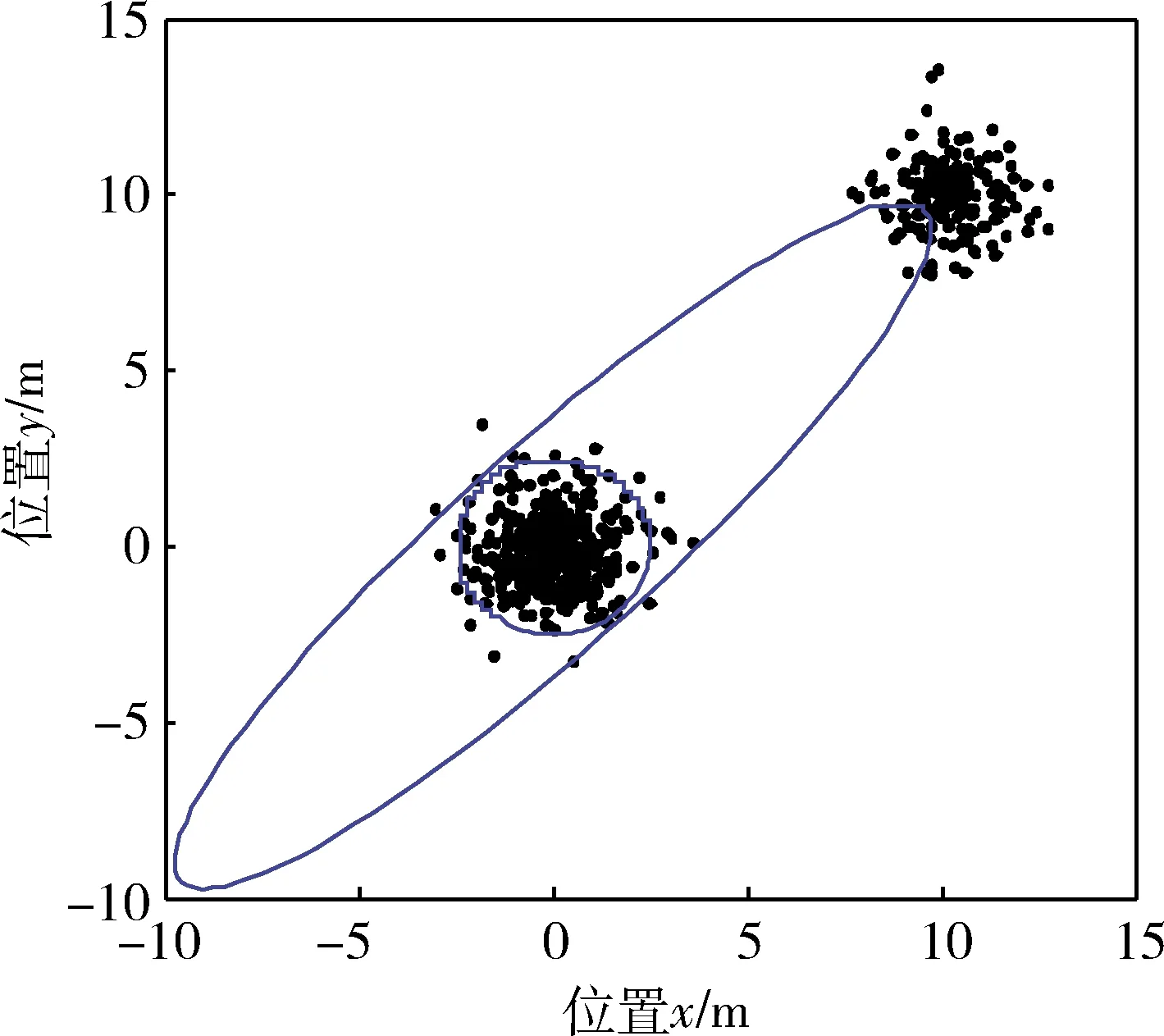
圖1 導航系統中被污染的樣本點

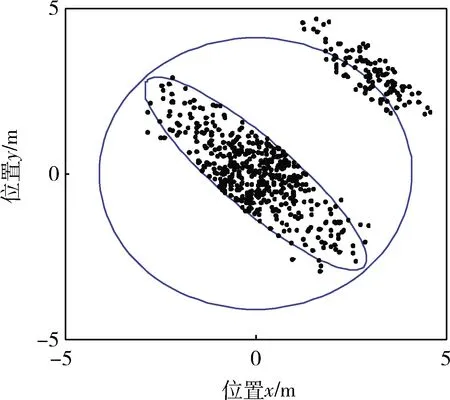
圖2 預白化處理后的樣本點分布

MD(Mahalanobis Distances)是一種經典的基于樣本點均值和方差的野值檢測方法，定義樣本點集的中心為c=[p1,p2]T，同一組狀態信息樣本點形成一擬合圓，令di=[di1,di2]T表示樣本點xi(i=1,…,m)到擬合圓的矢量，xi到擬合圓的距離為p3，那么di又可表示為di=(xi-c)(1-p3/‖xi-c‖)。MD野值檢測方法表示如下

(14)

(15)

(16)

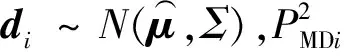
為此，人們提出了一種魯棒的野值檢測方法，魯棒PS(Projection Statistics)檢測法[9]，PS利用樣本點中值和中值絕對偏差(Median Absolute Deviation, MAD)來構造檢測方程：

(17)

式中：uk表示PSi檢測的基準方向，每個點都需對m個方向的投影進行檢測；PS方法受野值點干擾較小，當同時存在多處野值時也能夠準定位，其計算速度也較快。

2.3 魯棒PM估計濾波構建

將GM估計中的PS野值檢測方法應用到M估計濾波中，構建一種新的魯棒PM(Projection M-estimation)估計濾波。構建方法為：

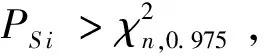
(18)

3 CNS/SAR/SINS組合導航模型

3.1 捷聯慣導誤差傳播模型

捷聯慣性導航系統是飛行器CNS/SAR/SINS組合導航系統的核心，SINS的誤差傳播方程也是組合濾波器模型的基礎。根據SINS誤差傳播方程構建組合系統的狀態方程，利用CNS和SAR的外部導航量構建量測方程，設計濾波器對慣導誤差進行估計。

以東北天地理坐標系為導航坐標系，CNS/SAR/SINS組合導航系統的慣導誤差傳播模型為[10-11]：

(19)

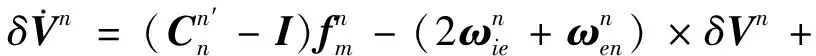
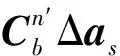
(20)

(21)

(22)

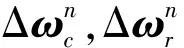
3.2 觀測方程

星光導航系統中星敏感器實際測得的星光矢量可表示為

(23)

星光矢量的理論測量值為：

(24)

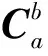
星敏感器對星光矢量的實際測量值rb與理論測量值pb有一定的偏差：

(25)

星光導航系統中一般將2個星敏儀正交安裝，把星敏感器實際測得的2個星光矢量rb1、rb2與理論測量值pb1，pb2相減，得到CNS/SINS的觀測量，INS的水平位置與SAR輸出的水平位置之差構成SAR/SINS量測信息[12]，則CNS/SAR/SINS系統的量測方程為

(26)

其中：vk為量測噪聲。

3 仿真校驗

將常規Kalman濾波、M估計線性濾波以及魯棒PM濾波分別應用于CNS/SAR/SINS組合導航系統進行數學仿真實驗。

仿真參數設置為：飛行器初始位置為東經116°，北緯38°，速度180m/s，方位角40°，俯仰和滾轉角為0°，飛行器有0.3m/s2的加速度和0.2(°)/s的轉彎角速度。捷聯慣導陀螺零漂不穩定值0.05(°)/h，加表零偏不穩定值100μg；星敏感器導航精度為20″(1σ)，SAR導航位置精度為20m(1σ)。仿真時間100s。

由于高空飛行器導航系統長時間工作，導航系統不可避免會出現各種野值、噪聲特性產生變化。下面通過設置不同的仿真條件，對3種線性濾波算法進行對比分析。

仿真條件1：

各導航設備的噪聲統計特性為受到污染的混合高斯分布，方差是原高斯分布的3倍，污染率為ε=0.2，混合高斯分布描述如下

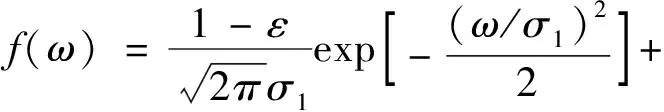
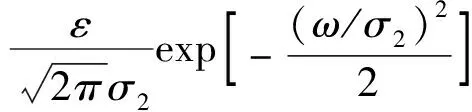
(33)

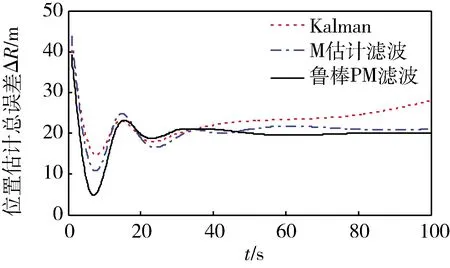
圖4 水平位置估計總誤差

仿真條件2：

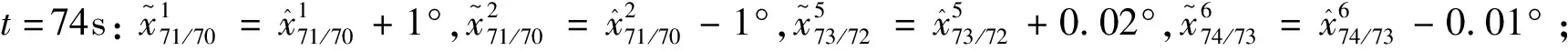
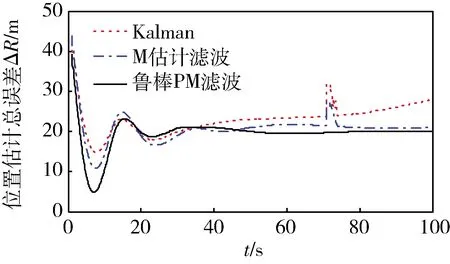
圖6 水平位置估計總誤差

仿真結果圖3～4表明，當導航設備的噪聲特性為混合高斯分布時，常規Kalman濾波呈發散趨勢、估計誤差較大，M估計濾波和魯棒PM濾波估計精度較高，驗證了M估計濾波和魯棒PM濾波對受污染的高斯分布噪聲具有魯棒性。

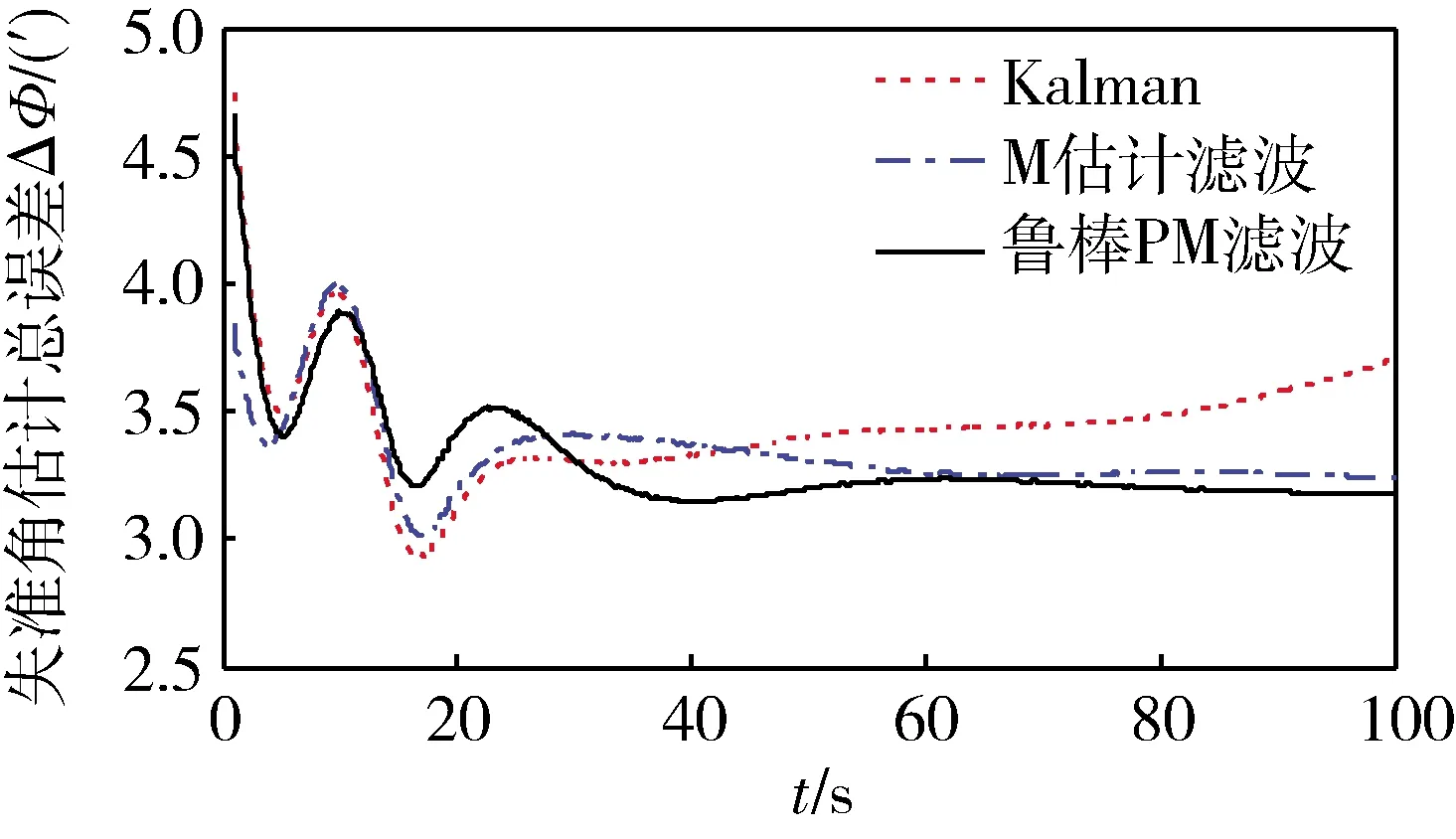
圖3 三向姿態失準角估計總誤差

仿真結果圖5～6表明，當導航系統中存在尖銳野值和結構野值時，常規Kalman濾波和M估計濾波對這些野值無法抑制，而本文提出的魯棒PM濾波使用了PS野值檢測方法和魯棒構架，可以對污染噪聲和多種野值進行有效抑制。

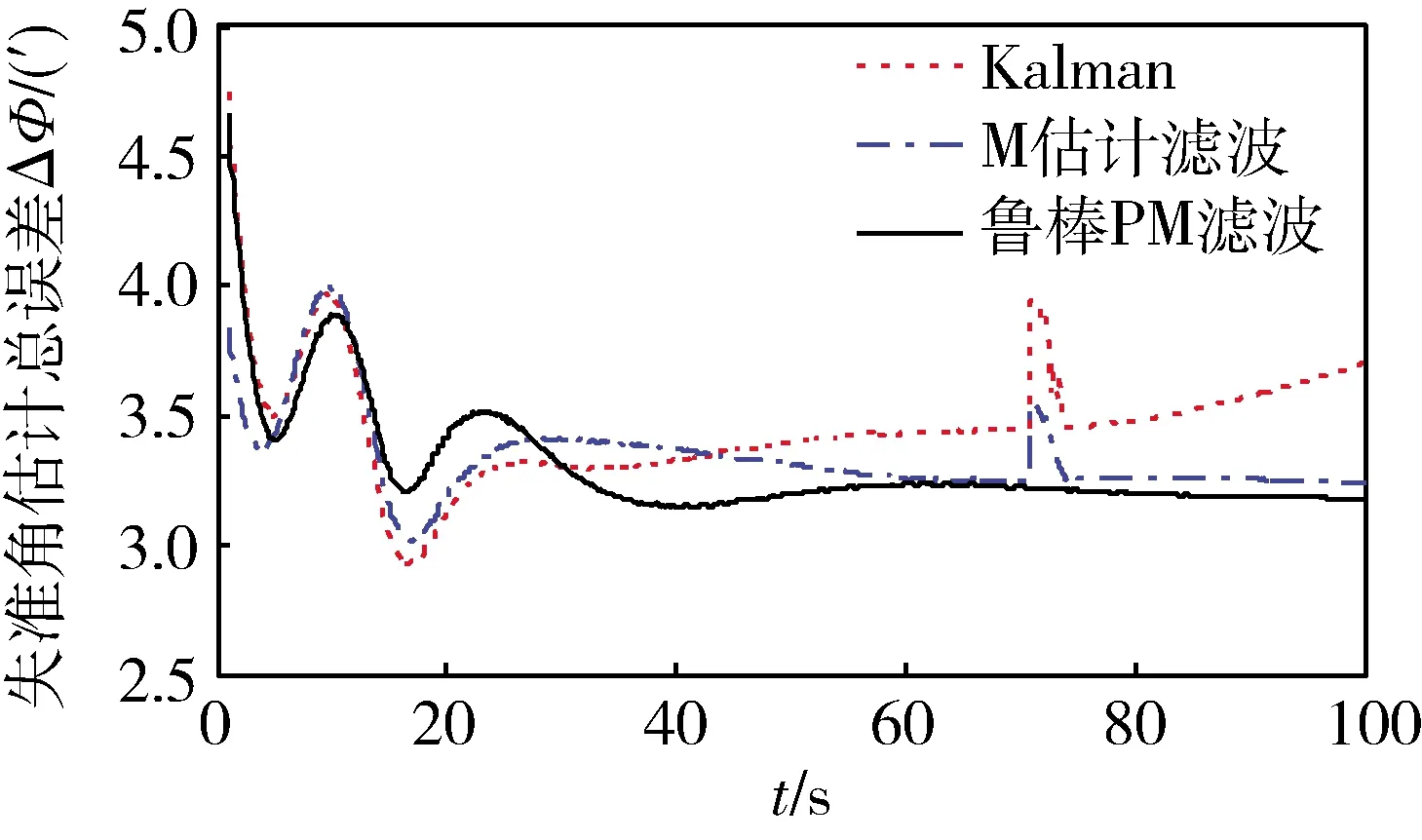
圖5 三向姿態失準角估計總誤差

4 結論

分析了傳統的M估計濾波在處理系統野值上的缺陷，借鑒了電力系統中的魯棒PS野值檢測方法，將魯棒PM估計濾波應用到組合導航系統中，以CNS/SAR/SINS非線性組合導航為應用背景，對常規Kalman濾波、M估計線性濾波以及魯棒PM濾波進行了對比分析。仿真結果表明，魯棒PM濾波能夠同時對受污染的高斯噪聲和多種系統野值進行抑制，具有較強的結構抗差能力。