高速飛行器編隊隊形快速成形設計方法

陸浩然 邱 薇 孫海亮 鄭 偉

1.國防科技大學，長沙 410073 2.北京宇航系統工程研究所，北京 100076 3.火箭軍研究院，北京 100089

0 引言

高速飛行器具有速度快、升阻比大、航程遠、機動性強等特點，已成為各種空間力量發展的重點方向。與單個飛行器相比，高速飛行器編隊在協同感知、博弈對抗、多維運用等方面具有更為廣闊的應用前景，因此研究其編隊控制問題具有重要意義。

針對多飛行器編隊控制問題，國內外學者開展了大量的研究，主要方法有PID控制、最優控制、高斯偽譜、滑模控制等。韋常柱等[1]建立了導彈的相對運動模型，將領彈的運動狀態視為輸入擾動，采用線性二次(LQR)最優控制理論設計了導彈編隊飛行保持控制器。張磊等[2]采用仿射非線性系統最優控制理論，設計了基于領彈-從彈法的多導彈編隊控制器，使之能夠在領彈機動地情況下快速、穩定地實現編隊隊形的形成和保持。Wen等[3]基于最小化隊形代價得到了一種隊形沖突預報和協調的算法，并通過仿真分析證明了其有效性。Wang等[4]考慮多種約束的編隊隊形最優軌跡，利用跟蹤算法實現了在多種擾動條件下的隊形形成與穩定控制。李文等[5]面向多導彈協同飽和攻擊同一目標需求，設計了綜合考慮脫靶量、攻擊時間、攻擊角度和視場角限制的三維協同制導律。但是，上述研究對象是彈道式或巡航式導彈，其氣動力常被忽略或簡化為常值，與實際偏差較大，而對于高速飛行器而言，先后經歷寬速域、大空域的復雜飛行環境，高動態氣動特性是必須重點考慮的因素。

近年來，偽譜法(Pseudospectral Method, PM)引起了學者們的廣泛關注，在航空航天飛行器軌跡優化領域得到深入研究。王芳等[6]基于高斯偽譜法，提出編隊形成-保持-攻擊一體化的時間最優控制算法，實現了導彈編隊協同攻擊全過程快速控制。姚寅偉等[7]提出了一種基于“初值軌跡生成+Gauss偽譜法+SQP求解NLP”的高超聲速飛行器多維再入軌跡優化方法，既利用了Gauss偽譜法收斂快#精度高的特點，又結合初值軌跡生成算法，彌補了Gauss偽譜法對初值敏感的不足。雷虎民等[8]提出一種自適應更新的偽譜法，以較小的網格規模獲得較高的精度，并成功應用于最優控制問題。

本文針對高速飛行器編隊控制問題，設計了一種基于偽譜法的編隊成形隊形自適應優化方法。該方法通過分析高速飛行器的運動狀態，利用最低能量原則和最小偏轉角度對編隊隊形成形的位置進行設計，避免了初始狀態與期望隊形偏差過大時問題無解的情況；同時設計出期望的隊形成形狀態，將原編隊控制問題轉化為軌跡設計問題，采用Radau偽譜法對軌跡設計問題進行求解；通過數值仿真驗證了該編隊設計方法的有效性，結果表明高速飛行器能在一定范圍內的初始狀態下形成穩定的空間構型。

1 動力學方程及約束

在地心坐標系下，高速飛行器運動方程為：

(1)

式中：r為地心距，是飛行器質心到地心的距離；λ和φ分別為飛行器所在位置的地心經度、地心緯度；V為飛行器相對地球的速度大小；γ為速度傾角，是速度矢量與當地水平面的夾角；ψ為速度方位角，是速度矢量與正北方向的夾角，順時針為正；σ為傾側角，是速度系與航跡系繞速度軸旋轉的角度，以逆時針為正；D和L分別為阻力加速度、升力加速度。

實際上，阻力、升力滿足以下關系式：

(L,D)=f(α,β,v,h)

(2)

式中：α為攻角，β為側滑角，h為飛行高度，均與飛行器當前運動狀態有關。需要說明的是，在仿真過程中，上述函數是通過對標準氣動參數插值得到的。

高速飛行器在大氣層內機動飛行時，除了需要滿足高度、速度等終端約束外，還必須滿足熱流、動壓、過載等過程約束條件。

1)熱流約束

高速飛行器在大氣層內飛行時，與來流發生劇烈碰撞和摩擦，導致了嚴重的氣動加熱問題。在理論研究中，一般選擇駐點熱流密度來表征氣動加熱的嚴重程度，如式(3)所示：

(3)

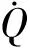
為避免駐點處熱流密度超出約束，應滿足：

(4)

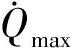
2)過載約束

高速飛行器在大氣層內飛行時，為避免出現結構性破壞，需對氣動過載加以約束，如式(5)所示：

(5)

式中：n為氣動過載，nmax為飛行器能承受的最大氣動過載，g0為地球引力加速度。

3)動壓約束

動壓是飛行器最重要的特征量之一，其極限值主要取決于熱防護材料強度和氣動控制鉸鏈力矩。動壓必須限制在一定范圍內，以確保表面絕熱材料結構不受破壞，不超過對應于控制氣動操作面所要求的最大鉸鏈力矩允許動壓。

動壓約束q的表達式為：

(6)

式中：qmax為約束的最大動壓。

2 編隊隊形快速成形實現方法

高速飛行器在編隊飛行過程中，期望隊形根據任務要求設計，當編隊開始時刻飛行器位置相對于期望隊形存在較大偏差時，如果對編隊成形隊形直接賦值，將會在初始狀態和氣動力約束下出現無解現象。針對該問題，本節分析編隊控制過程中飛行器機械能的變化，并以此為原則設計編隊成形時的隊形位置和過渡時間，確保從初始狀態到終端期望隊形存在可行解。

2.1 問題轉化

高速飛行器在大氣層內飛行時，主要受地球引力和氣動力作用，升力控制速度方向，阻力改變速度大小，動能轉化為熱能散掉，整個飛行過程中的機械能逐漸降低。因此，對于多飛行器編隊控制，將以最低能量飛行器作為參考，設計編隊成形狀態。

為確定編隊形成時的飛行器與初始時刻飛行器的對應關系，設計一種以最小偏轉角度為原則的飛行器標號識別方法。假定飛行器k的速度和速度傾角不變，經過一段時間Δt后到達一虛擬位置，計算該虛擬位置與起點連線的虛擬方位角ψ1k。對于一種確定的終端編隊飛行狀態，存在n!種不同隊形和對應關系的排列，分別計算該位置相對于起點的方位角ψk，并計算方位角偏轉角度絕對值|ψ1k-ψk|的總和。通過優化方法尋找最小方位偏轉角度的編隊隊形，從而確定初始時刻與編隊形成時刻飛行器的對應關系。

設計的隊形確定方案如下所示：

a)計算初始時刻各飛行器的機械能，找出能量最低飛行器，并按照機械能大小由低到高依次排列

i={i∈(1,2,…,n)|Ei=min(E1,E2,…,En)}

(7)

b)對機械能最低的飛行器，利用偽譜法優化T時間內的運動軌跡和終端狀態，使下式所示的指標J最優，其中T是選擇的編隊成形時間

(8)

c)若以機械能最低的飛行器T時刻狀態為參照，對于最終期望的編隊隊形，可以得到n種不同的編隊成形隊形，以及n!種“成形時刻—初始時刻”飛行器的一一對應狀態，利用下式求解不同情況下的方位角偏轉角度

(9)

d)尋找方位角偏轉角度最小的情形，確定飛行器間的對應關系

j={j∈(1,2,…,n!)|Ei=min(A1,A2,…,An!}

(10)

至此，確定了初始時刻飛行器的編號和狀態以及編隊成形時刻飛行器的編號和狀態，編隊成形過渡時間由T確定，將原編隊成形問題轉化為軌跡優化問題。

2.2 軌跡設計

本文采用Radau偽譜法，求解各飛行器滿足動壓、熱流、過載、終端狀態等約束的飛行軌跡，實現由散亂的初始狀態形成期望的編隊隊形。

在偽譜法中，取新的自變量τ∈[-1,+1]對時間做單位化，將間隔τ∈[-1,+1]劃分為由K個網格間隔[Tk-1,Tk]，k=1,…,K組成的網格，其中(T0,T1,…,TK)是網格點。

在每一個k∈[1,…,K]間隔內部，狀態量使用N+1次拉格朗日多項式逼近：

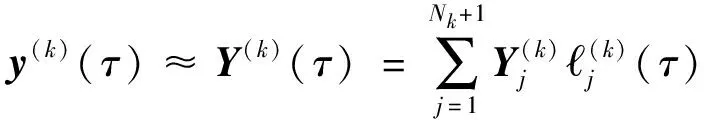
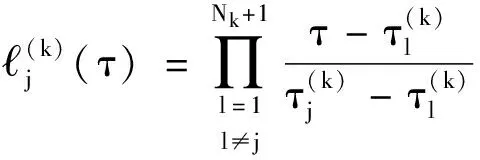
(11)

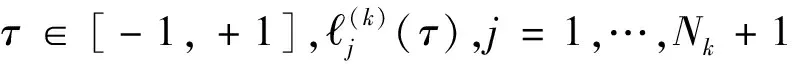
對狀態作微分可以得到：

(12)

目標函數為：

(13)

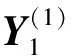
動力學方程為：

(14)

式中，i=1,…,Nk；Ui是控制量的近似，控制量由N+1階多項式逼近，D(微分形式)表示如下：

(15)

式中：i=1,…,Nk，j=1,…,Nk+1，k=1,…,K。

路徑約束為：

(16)

式中：i=1,…,Nk。

積分約束為：

(17)

式中：i=1,…,Nk，j=1,…,nq。

通過上述處理將原連續問題離散逼近，進一步求得關于離散優化問題的梯度、雅可比矩陣等信息，通過調用IPOPT、SNOPT等二階或一階求解器解決上述離散系統非線性優化問題。

3 仿真分析

不失一般性，以3個高速飛行器編隊初始控制為例驗證本文所提出算法的有效性，飛行器初始狀態如表1所示。

表1 高速飛行器初始運動狀態

其中，假設3個飛行器的氣動參數相同，其質量、參考面積、升阻力系數參照CAV-H。3個飛行器位于同一高度上，且編隊時的緯度相同，沿不同經度成一字形排列，相鄰兩個飛行器間的距離為10km。

令最低能量飛行器偽譜法求解的飛行時間T=30s，控制量為攻角、傾側角，設置范圍為0～30°，±90°，攻角和傾側角變化率范圍為±10(°)/s和±40(°)/s，采用GPOPS進行離散化處理，路徑約束包括過載、熱流、動壓約束，范圍分別為0～10g、0～104kW/m2、0～100kPa，相對求解精度設置為1e-4，并調用IPOPT求解器求解如上非線性規劃問題，仿真結果如圖1所示。

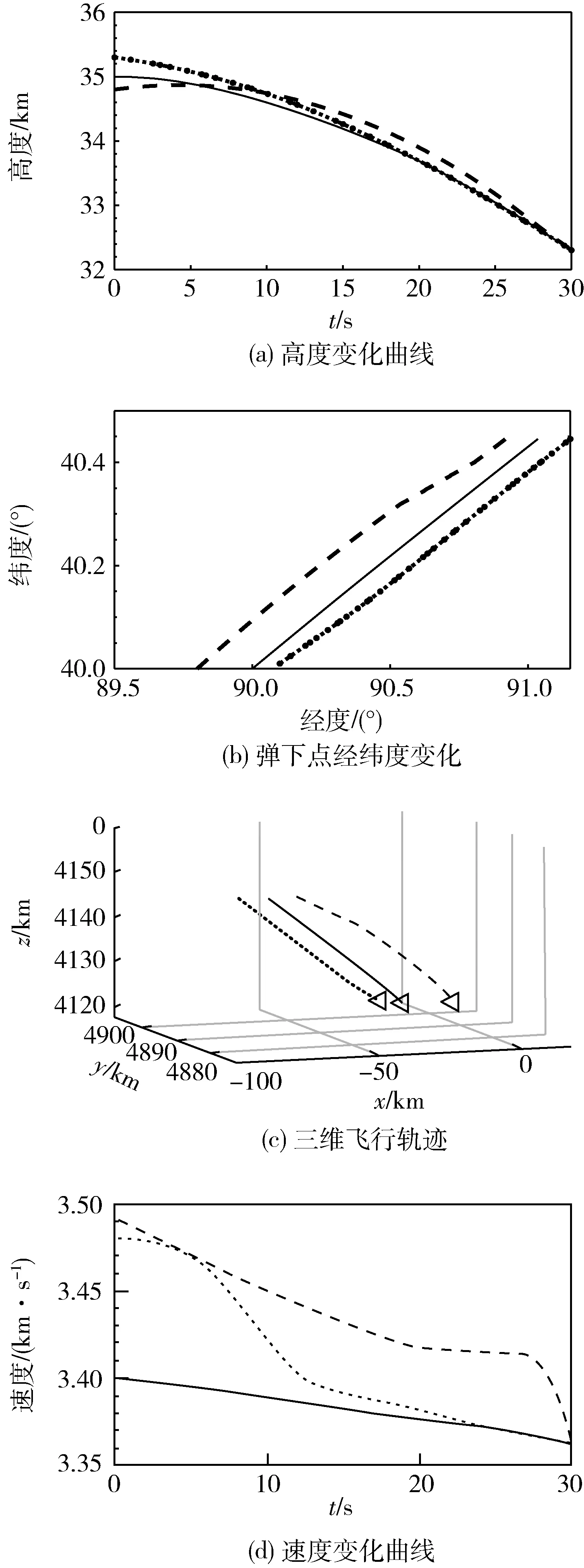
圖1 飛行器狀態變化歷程圖

圖1給出了3個飛行器狀態變化歷程，其中實線代表最低能量飛行器，點劃線為中間能量飛行器，虛線為最高能量飛行器。由結果可知，在高度上三者的變化相對較為平緩，其中點劃線所對應飛行器平滑過渡到實線的高度上，而虛線則相對而言有一個躍起的過程。在經緯度平面上，虛線相對實線有聚攏的趨向，點劃線則相對實線有一定的偏離。最終三者能夠形成期望的隊形，其三維圖像如圖1(c)所示，三角表示編隊成形時的位置。在圖1(d)中，可以明顯地看到虛線所對應的飛行器在軌跡末段有較大的機動減速過程，而點劃線所對應飛行器速度的變化集中于過渡前段，這與高度的變化規律是一致的。

攻角、傾側角變化歷程如圖2所示。由圖2(a)可知，點劃線對應飛行器的大攻角集中于軌跡前段，虛線對應飛行器集中于軌跡后段，與上述關于機動的分析一致。由圖2(a)，可以看到在前20s范圍內，虛線與點劃線的變化基本上相反。根據初始時刻對應飛行器的相對位置可以給出解釋，即虛線對應飛行器過于遠離最低能量飛行器，而點劃線飛行器則過于靠近，因此形成了2種不同的傾側角變化方式。

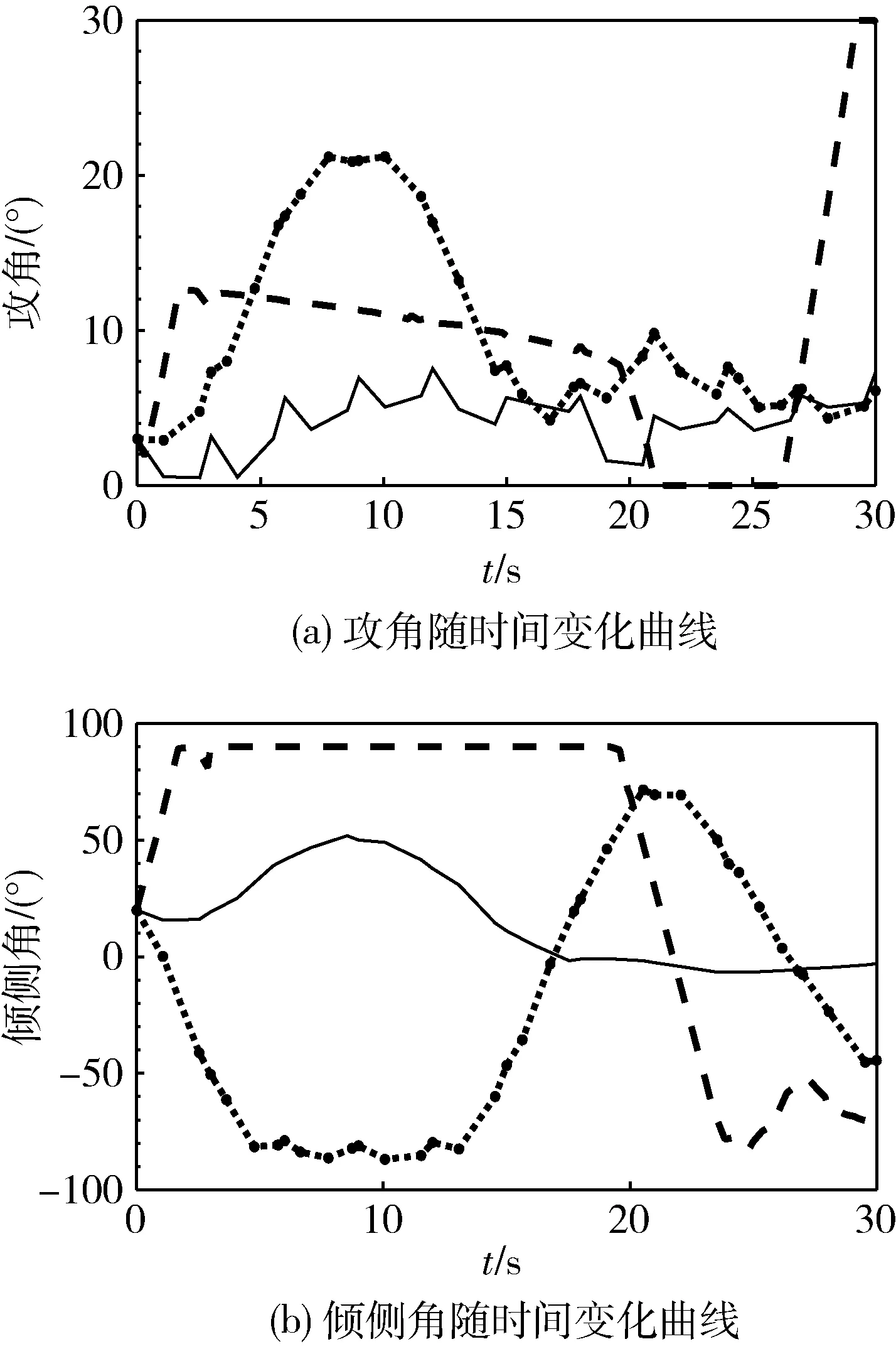
圖2 攻角和傾側角變化歷程圖

表2給出了飛行過程中過載、動壓、熱流約束的最大值。由計算結果可知，過載、動壓、熱流均滿足過程約束要求，其中動壓、熱流密度相對較小，而最大過載相則對較大，在7.09g左右，結合圖2可知，是由于虛線對應的飛行器在軌跡末段機動所致。

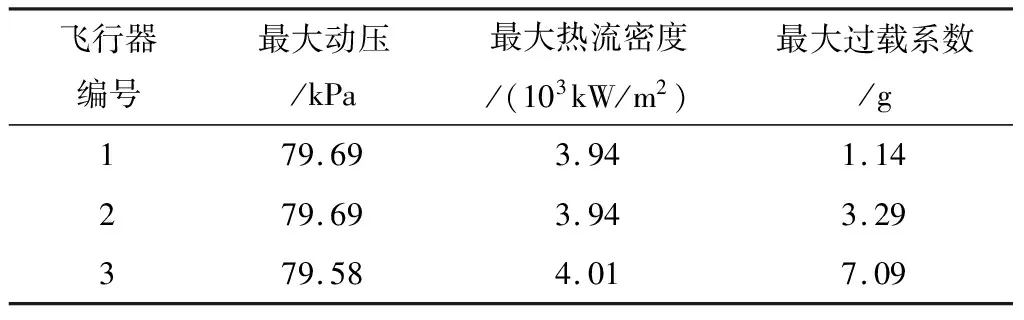
表2 飛行過程約束最大值

在飛行器不同初始狀態下，對本文所提方法的魯棒性進行驗證，認為初始時刻飛行器位置、速度在基本初始狀態下有如表3所示的偏差分布。

表3 初始運動狀態偏差分布

在飛行器不同初始狀態下，對本文所提方法的魯棒性進行驗證，認為初始時刻飛行器位置、速度在基本初始狀態下有如表3所示的偏差分布。同時，為更好的表現仿真打靶結果，定義多個飛行器系統的隊形偏差為：

(18)

式中：Hi0，λi0和φi0是由當前時刻最低能量飛行器和理想隊形為基準確定的其他飛行器的期望高度、經度、緯度，Hi，λi和φi為第i個飛行器的高度、經度和緯度。在達到期望隊形后，上述系統高度偏差ΔH、經度偏差Δλ和緯度偏差Δφ應當收斂為0。

100組仿真打靶結果如圖3所示。

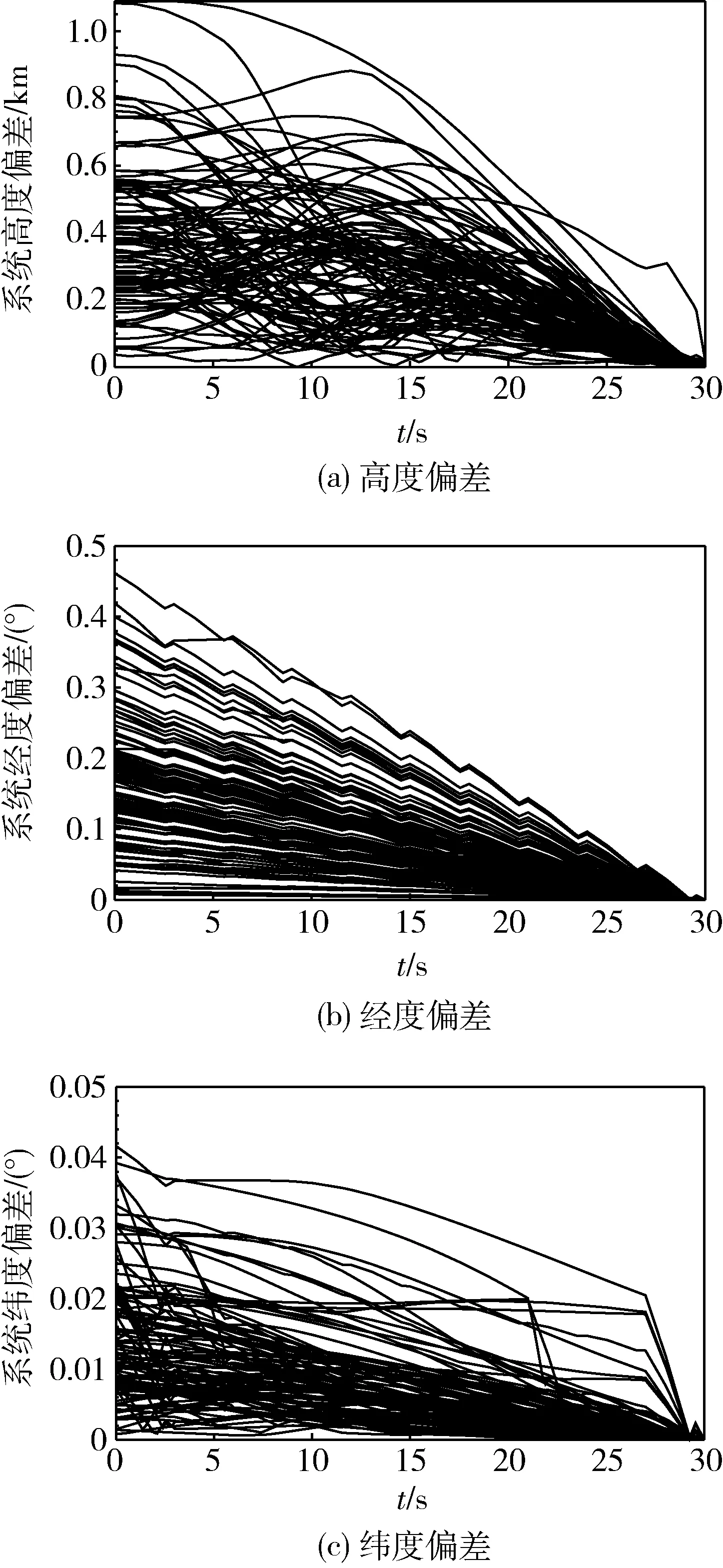
圖3 打靶仿真結果

可以看到，對于給定初始狀態偏差條件下的3個飛行器，經過上述方法后均可形成最終的穩定隊形。圖3(a)中所有曲線均在30s處收斂于0，即滿足最終隊形的同一高度要求。圖3(b)中，偏差同樣在30s處收斂于0，滿足穩定狀態下的經度要求。在圖3(c)中，可以看到絕大部分曲線呈緩慢下降趨勢，在30s處收斂于0，極少部分曲線其偏差變化集中于最后5s以內，但總體而言均同樣滿足穩定狀態下的緯度要求。

4 結論

研究了一種考慮多種路徑約束的高速飛行器編隊隊形快速成形設計方法，利用最低能量原則和最小偏轉角度原則確定了編隊形成時期望編隊隊形的位置和“成形時刻—初始時刻”飛行器的一一對應關系，避免了初始狀態與期望隊形偏差過大時問題無解的情況，從而將編隊成形問題轉化為軌跡設計問題，并基于偽譜法對多飛行器軌跡設計問題進行求解。仿真驗證了該編隊控制方法的有效性，結果表明多個高速飛行器最終能夠形成期望的穩定隊形，打靶結果表明該方法具有一定的魯棒性，能夠適應一定范圍內的初始狀態。