預防維護下裝配線平衡的多目標重啟變鄰域搜索算法
趙聯鵬 唐秋華 張子凱 蒙 凱
1.武漢科技大學冶金裝備及其控制教育部重點實驗室,武漢,4300812.武漢科技大學機械傳動與制造工程湖北省重點實驗室,武漢,430081
0 引言
裝配流水線常用于汽車、電器等產品的大批量生產,是制造型企業最基本的生產單元。裝配線的平衡程度直接影響制造系統的效率,關乎產品質量以及生產成本,因此使裝配線達到平衡狀態至關重要。裝配線平衡問題(assembly line balancing problem, ALBP)就是將所有基本工作單元分派到各個工位,以使每個工位在節拍(相鄰兩產品通過裝配線尾端的間隔時間)內都處于繁忙狀態。該問題自被提出以來就受到學者廣泛關注,BOYSEN等[1]根據求解目標將其劃分為四類,并衍生出一系列變體問題及相關理論,其求解方法多樣,可分為精確算法[2]、啟發式算法[3]以及元啟發式算法[4]。
由于設備損耗、不確定性因素的存在,在實際生產時機器會出現故障,又因為裝配線生產過程具有連續特征,故障一旦出現便會導致生產過程中斷,故需要對機器進行維護。設備維護通常分為糾正性維護(corrective maintenance, CM)和預防性維護(preventive maintenance, PM)。前者在設備發生故障后進行維修,屬于事后維護;后者利用機器診斷、定期檢查等技術對設備狀態進行監測,并有針對性地安排維修,該方法可以將機器故障事先排除,提高設備的可靠性,減少或避免停機損失[5]。
預防維護現已成為制造型企業普遍采用的設備維護方式。預防維護與車間調度的相互影響很大,集成預防維護和車間調度的研究近年來也大幅度增加。ALIREZA等[6]將預防維護與柔性流水車間調度進行集成優化,提出了融合遺傳算法與模擬退火算法的元啟發式算法,以最小化最大完工時間。WANG等[7-8]提出多目標禁忌搜索以及四種啟發式算法,分別求解預防維護與兩階段混合流水車間、雙機流水車間集成調度問題。同樣,在已知預防維護計劃前提下,也應考慮基于預防維護情形的裝配線平衡,以便在設備維護時迅速做出生產調整。面向該問題,蒙凱等[9-10]建立多目標優化模型,并提出了改進多目標灰狼算法與改進鯨群優化算法兩種群智能算法。ZHANG等[11]針對考慮預防維護的U型裝配線平衡問題,提出改進多目標JAYA算法。總體來說,針對預防維護下的裝配線平衡研究相對較少,并且求解方法主要集中在群智能算法的改進。仍然有必要對預防維護下的裝配線平衡問題進行深入研究,特別是面向問題獨有特征的分析,同時應拓展如局部搜索等求解方法,以結合問題本質特征,快速有效求解問題。
為此,本文提出了一種多目標重啟變鄰域搜索(multi-objective restart variable neighborhood search, MORVNS)算法,探索面向預防維護下裝配線平衡問題屬性的鄰域結構特征與Pareto前沿推進方法,并且將其與基本變鄰域搜索算法、改進多目標灰狼算法以及另外四種經典算法進行比較,以評估所提算法的有效性和優越性。
1 問題描述
1.1 預防維護下的裝配線平衡
相比正常工作,預防維護會使得工作工位減少、生產節拍增加以及工序調整,這時需根據工序間的優先關系確定操作序列,同時將相應工序重新分配到不同的工位,并保證正常工作和預防維護兩種情形下的生產效率。如圖1所示,某案例具有12道工序和4個工位,已知各工序操作時間及其優先關系。由于工位2需要進行預防維護,則工序[5 3 6 9]需要進行調整。

(a)各工序優先關系

(b)工序安排圖1 工序優先關系及安排Fig.1 Process priority relationship and arrangement
由此可以看出,正常生產和預防維護情形下的任務分配既具有一定的相同性,同時又具有極強的差異性。其中,相同性體現在:不同情形下的工序分配都必須滿足優先關系;各工位時間不能大于當前情形下的生產節拍。差異性主要體現在以下三個方面:
(1)預防維護情形下,至少有一個工位被維護,被維護工位沒有生產能力,其他工位能夠參與生產。考慮到工位維護會改變生產狀態,所以會導致一定時間的生產中斷,為縮短該調整時間,每次維護應暫停盡可能少的工位。
(2)預防維護下參與生產的工位減少,意味著該情形下的生產節拍不會小于正常工作時的生產節拍。
(3)預防維護工位的工序需調整到其他工位,而且其他工位上的工序也可能會被調整,以達到負載均衡的目的。因此工序調整數應盡量少,以減少調整時間并更好地保持生產連續性。
1.2 多目標優化模型
預防維護下的裝配線平衡優化正常工作、維護情形下的節拍與工序調整三個目標,基于此構建多目標優化模型,并做出以下假設:
(1)已知各個工序的操作時間與優先關系;
(2)各道工序必須并且只能夠被加工一次;
(3)在每一個工位上都能夠加工所有工序;
(4)裝配線是生產單一產品的單邊直線型;
(5)不考慮工序準備時間與工件移動時間;
(6)每次計劃必須且只能夠維護一個工位。
模型中,n為工序數;m為工位數;I是工序集合,I={1,2,…,n},i,k∈I;J是工位集合,J={1,2, …,m},j,l∈J,l為需要維護的工位序號;S是工作情形集合,S={0, 1,…,m},ω∈S,當ω=0時為正常工作的情形,ω=l時為對第l號工位預防維護的情形;Pn×n為優先關系矩陣,若工序i為工序k的直接前序則Pik=1,否則Pik=0;ti為第i道工序的加工時間;Cω是ω情形下的生產節拍;Aω為正常工作轉換到ω情形下的工序調整數量,當ω=0時Aω=0;Xijω是決策變量,表示在ω情形下,若工序i分配到工位j上則Xijω=1,否則Xijω=0。
基于上述定義,該問題多目標優化模型的目標函數可以表示為
z1=minCω=0
(1)
z2=minCω=l
(2)
z3=minAω=l
(3)
式(1)與式(2)分別表示最小化正常工作以及預防維護情形下的生產節拍;式(3)表示最小化由正常工作切換到某種預防維護情形時產生的工序調整數量,其計算依據下式:
(4)
式(4)通過將預防維護與正常工作情形下每個工位上的工序分配相比較,來計算該預防維護情形下的工序調整總量,以便進行生產準備。
多目標優化模型的約束條件可以表示為
(5)
(6)
(7)
(8)
(9)
式(5)為工序分配約束,表示每道工序都必須分配到一個工位并且只能分配一次;式(6)為工序優先關系約束,表示只有當某工序的所有緊前工序全部完成后才能對其進行分配;式(7)與式(8)為工位分配約束,表示工位不被維護時應至少被分配一道工序,進行維護的工位不應該被分配任何一道工序,因此被維護工位上的總操作時間為零;式(9)為節拍約束,表示在ω情形下任何一個工位上的總操作時間都不能大于生產節拍。
2 多目標重啟變鄰域搜索算法
變鄰域搜索算法(VNS)[12]是一種經典的局部搜索算法,因其結構簡單、易于實現且參數較少等優點,自提出以來就被廣泛應用于生產調度、路徑規劃等組合優化問題,它通過對多鄰域進行特定形式的搜索來找到問題的滿意解。裝配線平衡問題是典型的NP-hard問題,當問題規模較大時需要運用近似算法對其進行求解,在該問題研究領域,變鄰域搜索算法已被應用于優化雙邊裝配線平衡問題[13-14]中工人數量、線長以及生產節拍。
基本變鄰域搜索算法通過設計擾動算子來避免陷入局部最優。本文所提算法設計重啟算子以替代擾動算子作為跳出局部最優的手段,并對多種鄰域結構的選擇、組合與搜索策略進行研究。
2.1 初始化與解碼
2.1.1初始解的生成
預防維護下裝配線平衡問題的可行解包括正常工作、設備維護情形下的工序安排以及工序調整三部分,解的表達采用滿足優先關系的實數編碼[9]。在局部搜索算法中,初始解通常由隨機或啟發式方法獲得,從一個性能較優的初始解出發能夠更快找到滿意解。
考慮多目標和裝配線平衡問題的特性,本文所研究問題的初始解利用啟發式規則與隨機編碼相結合的方式生成。首先按照最短操作時間(shortest processing time, SPT)規則[15]、最長操作時間(longest processing time, LPT)規則[16]、優先位置權重(ranked positional weight, RPW)規則[17],分別混合最短與最長操作時間和優先位置權重規則隨機編碼生成6種操作排序方案,由此得到36個不同的待選初始解。然后,利用“擂臺賽法則”[18]依據它們的目標函數值進行非支配排序,找出初始非支配解集,并計算解集中各解與其他解之間的距離,最終選出距離之和最大的解作為初始解。
2.1.2固定工位下的動態迭代解碼
在求解預防維護下裝配線平衡問題中的不同工作情形下的生產節拍時,其本質是求解第二類裝配線平衡問題,即在給定工位數時最小化生產節拍。當操作序列確定后需要將各工序分配到各工位并獲得該序列下的最小生產節拍。由于每種生產情形下工位數目固定,又因同一序列的分配方案有多種,故不能采用增加工位的方式進行解碼,所以采用固定工位下的動態迭代解碼。基于某一情形下的工序操作序列,具體解碼步驟如下。
(1)依據下式計算該操作序列下的理論最小生產節拍:
(10)
并令當前節拍C=CE。
(2)按照當前節拍C將該序列中的操作依次分配到各工位,直至分配到第(m-1)號工位滿足當前節拍要求,然后將剩余操作全部依次分配給第m號工位。
(3)計算此時每個工位上的總操作時間Tj與T′j,后者的計算公式如下:
T′j=Tj+t1(j+1)
(11)
其中,t1(j+1)表示此時第(j+1)個工位上的第一道工序的操作時間。
(4)令C′=maxTj,C″=minT′j,若C′≤T″,那么C″就是該操作序列下的最優生產節拍,此時的分配方案也為該操作序列下的最佳分配方案;若C′>C″,那么,令當前節拍C=C″,并重復步驟(2)~步驟(4)。
針對每種情形,固定待維護工位和可工作工位,運行上述解碼,可獲得目標值(C0,Al,Cl)。其中,C0為正常工作情形下的生產節拍;Cl為對l號工位進行維護的情形下的生產節拍;Al為兩種情形切換時的工序調整數量。
2.2 接收準則
新解的接收準則是:若該解能支配當前Pareto前沿解集中的某些解,或者與其中所有解互不支配,那么就將該解放入前沿解集并刪除被其支配的所有解,否則丟棄該解;在新解與當前非支配解集中的所有解互不支配時,則將其保留在前沿解集中,但不認為前沿解集獲得實質性推進;只有當前Pareto前沿解集中全部或者部分解被新解支配時才認為其發生實質性推進。
2.3 變鄰域搜索算子
在對多鄰域進行搜索時,若鄰域結構數量太多則會增加計算的時間成本,反之將會導致對解空間探索不完全,最終遺失滿意解。因此,在進行算法設計時必須考慮以下三點內容[12]:
(1)設計恰當數量并且針對問題屬性的鄰域結構;
(2)確定所采用的多種鄰域結構的排列組合形式;
(3)采用面向問題屬性尋優能力最好的搜索策略。
在本文所提算法中,對上述內容進行深入研究,并最終使算法展現出相對較好的性能。
2.3.1鄰域結構的選擇
針對裝配線平衡問題,現已有發展成熟且性能良好的鄰域結構,如互換算子、后插算子以及前插算子。在搜索階段,通常為了追求運行速度而忽略鄰域解的可行性,一般采取修復機制使不可行解轉換為可行解,這種設計方法不僅降低了產生可行解的概率又增加了計算復雜度。修復機制如同設備管理中的糾正性維護,本文在設計鄰域算子時運用預防維護思想,選取互換、后插與前插三種鄰域結構,并根據工序優先關系設計一次互換與多次互換、一次后插與多次后插、一次前插與多次前插六個算子以生成可行鄰域解,并且避免各算子鄰域空間出現重疊現象,消除重復操作帶來的時間損失。
同時,本文設計了一種新型鄰域結構,稱為重排式鄰域算子。已知某一操作序列,隨機選擇其中任意兩個位置,分別以近前端、近后端為起止點截取子序列,并根據子序列中各操作之間的優先關系形成部分優先關系矩陣,基于此對子序列進行重新排列得到新序列,如圖2所示。該例中起點為3、終點為9,初始子序列包含操作為[6 3 4 7 8 5 9],根據優先關系重新排列之后得到新的子序列[4 5 9 3 6 7 8],對應地,由初始序列[1 2 6 3 4 7 8 5 9 10 11 12]得到新的可行鄰域解序列[1 2 4 5 9 3 6 7 8 10 11 12]。
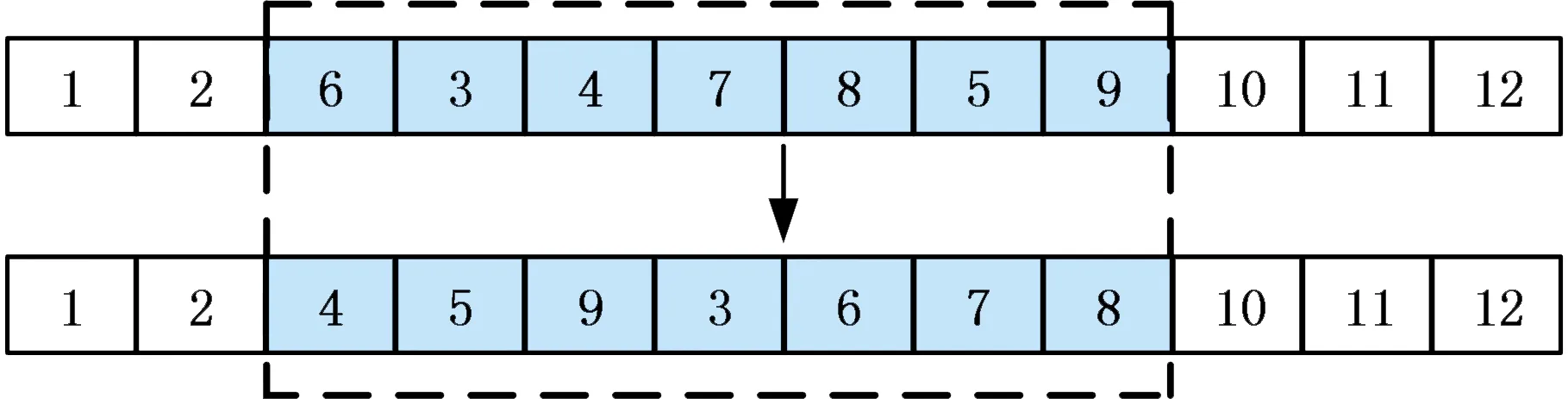
圖2 重排式鄰域算子實例Fig.2 Examples of rearranged neighborhood operators
2.3.2鄰域結構的排序
所提算法采用四類七個鄰域結構,除重排式鄰域結構之外,實現了互換、后插與前插算子的鄰域解空間完全沒有交叉部分。而重排式鄰域結構隨機性大,其鄰域解空間與其他三類算子的解空間有部分重疊,在其余算子探索不到的解空間,該結構起一定的補足作用。
大量實驗證明,根據工序優先關系實現的四類鄰域結構性能由優到劣依次為重排、互換、后插和前插,在鄰域搜索階段多種鄰域結構按此順序進行排列,以保證盡快找到滿意解。
2.3.3搜索策略的選擇
多鄰域結構的搜索方式通常有三種,分別是每次迭代隨機選擇一種鄰域結構進行探索的隨機鄰域搜索(stochastic neighborhood search, SNS)策略、交替進行的變鄰域搜索策略和對多種鄰域結構全部探索的全局鄰域搜索(global neighborhood search, GNS)策略。
面向預防維護下裝配線平衡問題,鄰域搜索策略采用交替搜索。理論上,假設選取K種不同的鄰域結構,在每次迭代時隨機搜索策略的計算復雜度為1,該策略時間成本最低;全局鄰域搜索策略的計算復雜度為K,時間成本最高;而采用交替搜索策略時計算復雜度在區間[1,K]內,時間成本也在其他兩種策略之間。采用三種搜索策略展現出的性能也將通過實驗算例進行驗證說明。
當鄰域結構選擇、組合以及搜索策略確定之后,隨即實現重啟前的變鄰域搜索階段(variable neighborhood search before restart, VNSBR),使它在算法中承擔重啟前的探索工作,并依據接收準則對新解進行判斷。偽代碼如下所示。
算法1VNSBR
1: Input:Ω,Nh(h=1, 2,…,K),POS
2: Begin:
3:d=0;
4: Forh=1 toKdo
5:Ω′=Nh(Ω);
6: If ?π∈POS:Ω′πthen
7:POS←POSπ∪Ω′;
8:Ω←Ω′ ∧d=0;
9: break
10: Else If ?π∈POS:πΩ′then
11:d←d+1;
12: Else
13:POS←POS∪Ω′;
14:d←d+1;
15: End If
16: End For
17: Output:Ω,POS,d
算法1中,Ω為被探索解;Ω′是鄰域解;Nh表示第h種鄰域結構;POS為當前Pareto前沿解集;POSπ表示解π在POS中的相對補集,是由POS中所有不同于π的解組成的集合;d用來記錄前沿解集連續未發生實質性推進的代數。
2.4 重啟算子
由于接收準則的本質是貪心策略,所以算法容易陷入局部最優。基本變鄰域搜索(basic variable neighborhood search, BVNS)算法采用擾動算子在每次尋優前對被探索解進行擾動得到中間解,從而獲得全新的鄰域解空間并進行探索,從而達到跳出局部最優的目的,但擾動具有隨機性,中間解性能有時會劣于當前解,所以增加了尋優過程的波動性。
為跳出局部最優,實現Pareto前沿解集的推進并同時保證算法穩定性,本文設計了一種新型重啟算子來替代擾動算子。
2.4.1自適應閾值
非支配解集連續未獲得實質性推進的代數是判斷何時重啟的關鍵,將它作為重啟算子的啟動閾值,記為g。若閾值取值過小,將導致頻繁執行重啟算子并錯過滿意解;若閾值取值過大,則會遲遲不重啟從而無法跳出局部最優,浪費CPU時間[19]。
在算法運行過程中,解的性能會隨著尋優次數的增大逐漸變優,因此在尋優后期相比前期更容易陷入局部最優。針對不同規模的裝配線平衡問題,陷入局部最優的可能性與工序數n、工位數m、操作時間不同的工序個數a以及優先關系約束強度R有關。在確定上述因素與重啟閾值的函數關系之后,當前尋優代數自適應重啟閾值g依據下式確定:

(12)
(13)
(14)

以基準案例Hahn中53工序4工位、Arcus2中111工序12工位以及Scholl中297工序26工位情況為例,重啟算子中自適應閾值g隨著算法迭代次數r動態變化曲線如圖3所示。圖3中,go為關于迭代次數的實際閾值函數。圖3顯示,隨著迭代次數r的增大,go曲線的斜率不斷減小,并且在尋優前期下降迅速,中后期趨于緩慢,這說明前期非支配解集能夠快速向真實前沿推進,中后期逐漸接近真實前沿。因此go的增長趨勢在不斷減緩,且向上取整后得到的每個g值持續代數增大。自適應g值曲線動態變化與算法在求解過程中陷入局部最優的趨勢吻合。
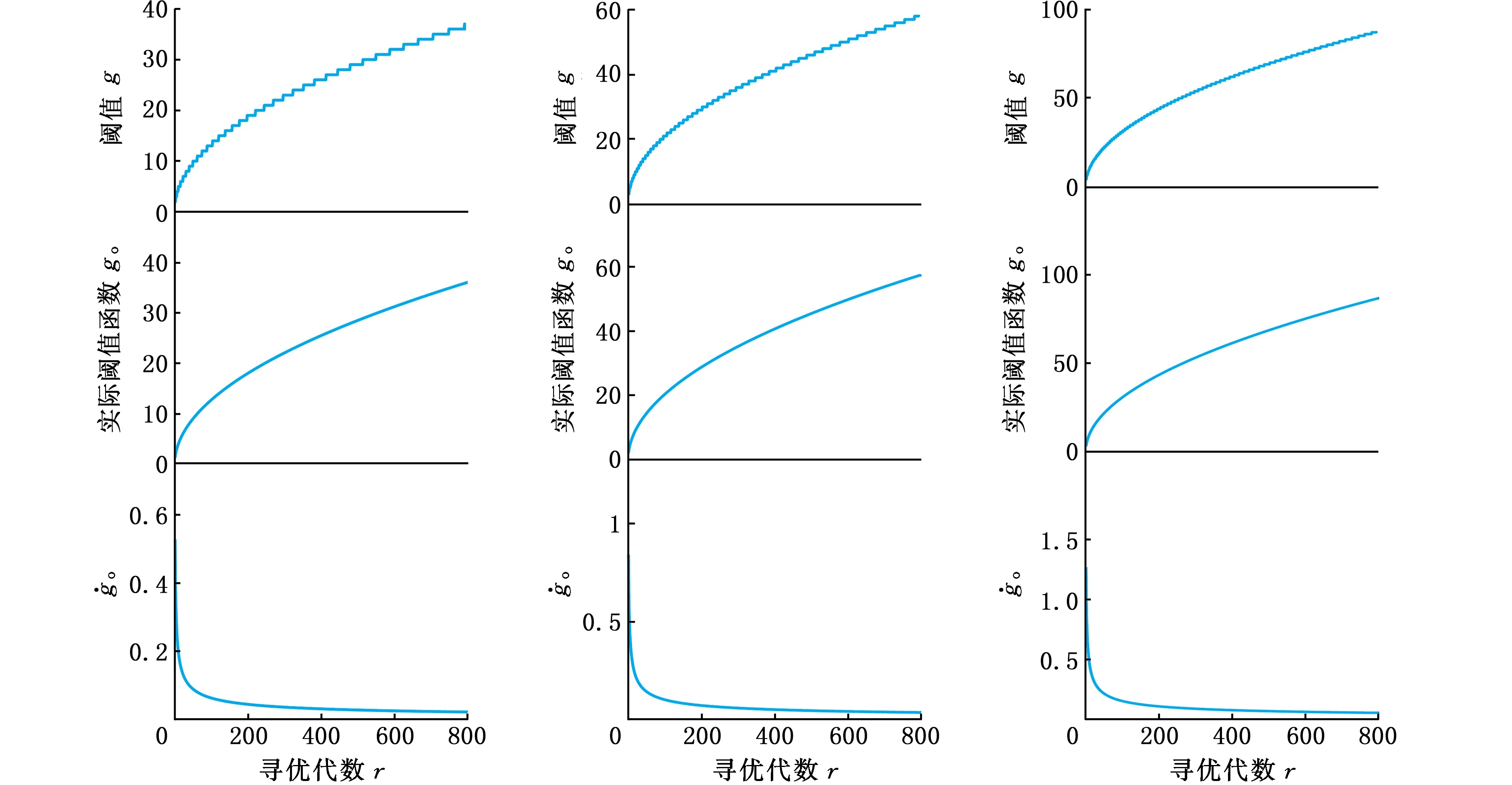
(a)Hahn(53工序4工位) (b)Arcus2(111工序12工位) (c)Scholl(297工序26工位)圖3 不同規模案例值曲線Fig.3 Curves of the values of g,go and for different scale cases
2.4.2自適應鄰域結構
當d>g時,執行重啟算子,即在當前非支配解集中隨機選擇一個候選解并記錄此時刻的重啟時間節點tr,并進入重啟后的變鄰域搜索(variable neighborhood search after restart, VNSAR)對候選解進行探索。與VNSBR階段不同的是該階段的多種鄰域結構是自適應的,每一次執行重啟更新該階段的鄰域結構規模時依據下式進行:
(15)
式中,Round(·)表示四舍五入取整。
式中,KM隨尋優進程動態變化,表示當前時間節點重啟執行后的鄰域搜索階段的鄰域規模;Tt是算法最大尋優總時間;K為全部鄰域結構的個數。
隨尋優進程的推移,該階段鄰域空間不斷擴大,從開始時只有性能最優的重排式鄰域空間逐步擴展到全鄰域空間。這是因為在尋優前期,重啟之后要立即將探索重點放在更容易產生滿意解的鄰域空間中以快速跳出局部最優,到中后期非支配解集中的解已接近滿意解,此時要將探索重點放在更廣闊的鄰域空間中,防止滿意解丟失。
2.4.3基于空間距離的選擇策略
在執行完畢重啟算子與重啟后的變鄰域搜索后,可以獲得最新的Pareto前沿解集。此時,為確保進入下一次重啟前的變鄰域搜索階段的候選解具有良好的多樣性,本文基于空間距離最大策略從當前非支配解集中選擇候選解。
每個解的適應度值(C0,Pl,Cl)都可視為三維空間中的一個點。顯然,Pareto前沿解集中與所有解距離之和最大的解就是位于最不擁擠區域的解,即為當前解集中多樣性最好的解,選此為候選解進入下一次重啟之前的變鄰域搜索階段。至此,多目標重啟變鄰域搜索算法執行完畢,其偽代碼如下所示。
算法2MORVNS
1: Input:n,m,R,Pn×n,ti
2: Begin:
3: Generate aninitialPOS;
4: Find the initial solutionΩ;
5:d=0;
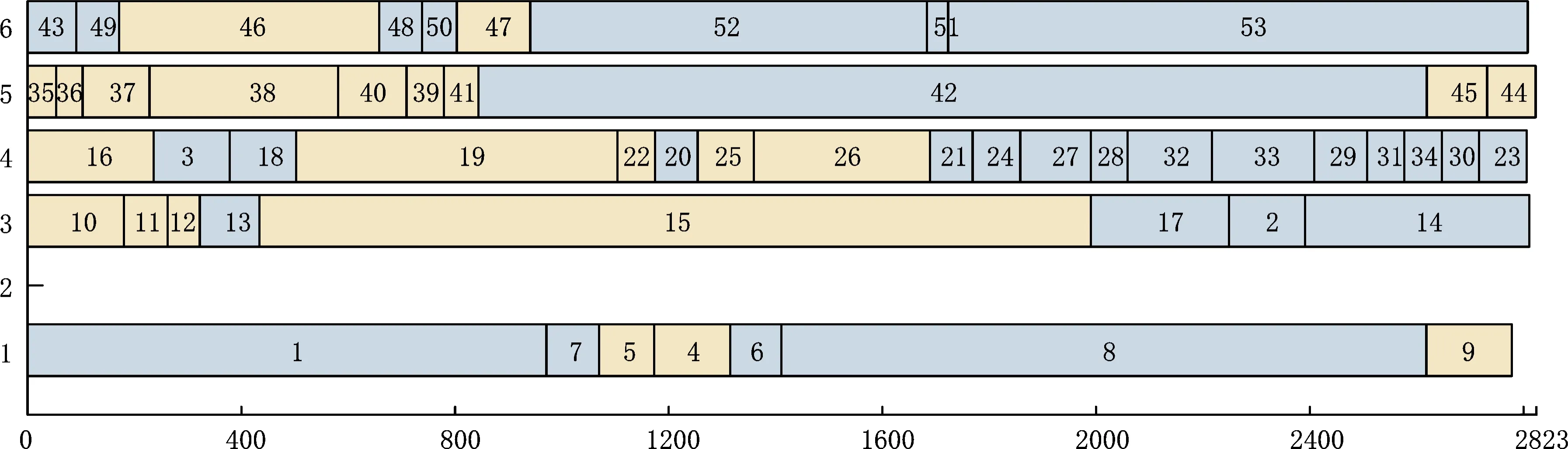
6: Whiletp 5: Forr=1 toβdo 6:g=G(n,m,Pn×n,ti); 7: (Ω,POS,d)=VNSBR(Ω); 8: Ifd>gthen 9: (Ω,POS,d)=VNSAR(Ω); 10:S=D(POS); 11: End If 12: End For 13: End While 14: Output:POS 算法2中,tp表示算法當前尋優總時間;β為足夠大的正整數;G為閾值g的生成函數;D為基于空間距離的候選解選擇函數。 為證明重啟算子、交替搜索策略以及多目標重啟變鄰域搜索算法的有效性和優越性,本文采用MATLAB R2018a編程,電腦配置為:Intel(R) Core(TM) i5-6200U CPU @2.30GHZ 2.40GHZ and 4.00GB RAM;預防維護情形全部基于裝配線平衡問題標桿案例生成,且每次計劃隨機選擇一個工位進行維護,標桿案例數據來自裝配線平衡專業網站[20];在進行算法對比時,選取30個案例進行實驗,每個案例運行8次,算法運行的終止條件設置為tp≥Tt,算法最大尋優總時間Tt=ρn2/1000,其中ρ=10。 以案例Hahn中53工序6工位情況的運行結果來說明預防維護下裝配線平衡多目標優化模型的優勢,其甘特圖見圖4。其中,橫軸表示每個工位上的工序操作時間,縱軸表示工位序號;圖4a表示正常工作情形下的工序安排,圖4b表示對工位2進行維護的工序安排。 (a)正常工作時最佳工序安排 (b)預防維護時最佳工序安排圖4 案例Hahn(53工序6工位)不同情形下的工序安排Fig.4 Tasks arrangement of Hahn(53 process 6 work station) in different scenarios 由圖4可知,該方案目標值為(2400, 23, 2823),說明正常工作的生產節拍為2400個單位時間,工位2維護情形的生產節拍為2823個單位時間,狀態切換時對23道工序進行了調整。若不考慮預防維護,當某工位發生故障時需要對其進行糾正性維護,此時整條線處于停工狀態。假設對一個工位維護的時間為x小時,產線的產值為每小時e萬元,則直接損失ex萬元。當考慮預防維護來進行裝配線平衡時,維護與生產在相同時刻進行,則損失僅為工序調整所需時間與成本,調整時間遠小于工位維護時間,隨行夾具以及各裝置調整成本也遠遠小于工位維護成本,由此可見,與不考慮預防維護的裝配線平衡相比,將預防維護提前考慮,能有效保證生產連續性、降低維護時的損失。 為全面評價算法的性能,本文選取世代距離(GD)DGD、逆世代距離(IGD)DIGD和超體積率(HVR)RHVR來判斷算法所得Pareto前沿解集的優劣[21]。 (1) 收斂性評價指標DGD用來衡量算法所求得的近似前沿解集Su與真實Pareto前沿解集之間的逼近程度。DGD(Su)值越小,說明Su與真實前沿PTP逼近程度越高,收斂性越好。計算如下: (16) (17) (2)逆世代距離DIGD同時評價解集收斂性與分布性,通過衡量真實前沿逼近Su的程度來判斷Su的優劣。DIGD(Su)越小,說明解集Su的綜合性能越好。計算如下: (18) (19) (3)綜合性評價指標RHVR通過計算Su與參考點σ形成的超體積占真實前沿PTP與參考點σ形成的超體積的比率。參考點σ應該被所有的解支配,將所有解進行歸一化后,選取(1,1,1)為參考點。RHVR(Su)值越接近1,說明Su的綜合性能越好。計算如下: (20) (21) 式中,VHV為解集S與參考點σ圍成的超體積;VOL(·)為勒貝格測度。 3.2.1搜索策略的有效性 為驗證多鄰域結構搜索時交替搜索策略的有效性,將MORVNS與多目標重啟隨機鄰域搜索算法(MORSNS)以及多目標重啟全局鄰域搜索算法(MORGNS)進行對比實驗。為確保實驗的公平性,算法均采用所設計的重啟算子、相同的鄰域結構和排列方式以及初始解生成策略。 采用不同搜索策略的算法分別對30個標桿案例進行8次對比實驗,所有基準案例所得結果GD、IGD以及HVR的均值的95%置信區間如圖5所示。由圖5可以看出,算法MORVNS獲得的非支配解集相比于算法MORSNS和MORGNS獲得的非支配解集在GD、IGD以及HVR評價指標上都具有良好的表現,這說明多種鄰域結構的交替搜索策略的性能優于隨機鄰域搜索以及全局鄰域搜索策略。 圖5 三種算法30個案例的GD、IGD與HVR均值的95%置信區間Fig.5 95% confidence interval for means of GD、IGD and HVR in 30 cases of three algorithms 3.2.2重啟算子的有效性 為了證明重啟算子的有效性,將所提多目標重啟變鄰域搜索算法(MORVNS)與多目標基本變鄰域搜索算法(MOBVNS)進行對比實驗。為確保實驗的公平性,MORVNS與MOBVNS均采用相同初始解生成方法和搜索策略、鄰域結構及其組合方式,并且在MOBVNS中根據性能較好的重排式鄰域結構設計擾動算子。 兩種算法對比結果通過30個案例的GD、IGD與HVR均值的95%置信區間圖顯示,如圖6所示。從圖6中可以看出,MORVNS得到的Pareto前沿解集的收斂性、多樣性以及綜合性能都顯著優于MOBVNS得到的非支配解集,因此,為跳出局部最優所設計的重啟算子是有效的。 圖6 兩種算法30個案例的GD、IGD與HVR均值的95%置信區間Fig.6 95% confidence interval for means of GD、IGD and HVR in 30 cases of two algorithms 為了能夠更好地分析所提出算法的綜合性能,將所提多目標重啟變鄰域搜索算法與改進多目標灰狼算法(IMOGWO)[9]和多目標粒子群算法(MOPSO)、多目標模擬退火算法(MOSA)、多目標禁忌搜索算法(MOTS)、帶精英策略的快速非支配排序遺傳算法(NSGA-Ⅱ)[22]進行對比實驗。其中,MOSA與MOTS兩種局部搜索算法均采用和本文算法相同的鄰域結構以及初始解生成方式。 在實驗進行之前,運用Minitab 18中田口實驗方法確定各個算法之中的參數,由于所提算法參數自適應,所以不對其進行參數校驗。各對比算法參數校驗結果如表1所示。 表1 各測試算法參數校驗結果Tab.1 Parameter validation results of test algorithms 在各對比算法參數確定之后,對30個案例進行實驗得到的結果如表2所示,所選取的評價指標GD、IGD以及HVR的均值的95%置信區間如圖7所示。 分析表2與圖7可知,所提算法MORVNS獲得的非支配解集相比其余測試算法所得的非支配解集的GD值與IGD值更接近于0、HVR值更接近于1,這說明所提算法在解決預防維護下裝配線平衡多目標優化問題上具有出眾的表現,所得非支配解集擁有較好的收斂性以及多樣性。 表2 各測試算法實驗結果Tab.2 Experimental results of test algorithms 圖7 各測試算法30個案例的GD、IGD與HVR均值的95%置信區間圖Fig.7 95% confidence interval for means of GD、IGD and HVR in 30 cases of test algorithms 以大規模標桿案例Scholl中具有297工序26工位的情況為例說明所有測試算法獲得的Pareto解集在三維空間中的分布狀態,如圖8所示。 圖8 Pareto前沿在三維空間中的分布Fig.8 Distribution of Pareto front in 3D space 分析圖8可知,MORVNS得到的非支配解集在一定程度上能夠支配改進多目標灰狼算法以及其余四種經典多目標算法得到的前沿解集,并在收斂性較好的基礎上獲得數量較多的滿意解。 綜上所述,所提算法獲得的前沿解集具有較好的綜合性能,因此所提MORVNS能夠獲得具有競爭性的Pareto前沿解集。 本文以最小化設備正常工作、預防維護情形下的生產節拍以及工序調整為目標,構建預防維護下裝配線平衡的多目標優化數學模型,并提出多目標重啟變鄰域搜索算法來解決該問題,所提算法具有以下特點: (1)實現四類能夠直接生成可行解的鄰域算子,并根據各算子性能對其進行組合排序。 (2)探索多鄰域結構搜索策略,并從理論與實驗兩方面驗證交替搜索為最有效的搜索方式。 (3)設計重啟策略跳出局部最優,并以自適應重啟閾值作為判斷是否重啟的條件。 (4)參考尋優進程逐漸擴大重啟后的鄰域空間,并基于空間距離選擇進入下次重啟前的待探索解,從而有針對性地對特定解與特定鄰域空間進行重點搜索。 實驗證明本文所提算法能獲得綜合性能較好的非支配解集。決策者可以在不同性能且具有競爭性的多個非支配解中進行選擇,更好地指導實際生產。后續工作將對預防維護與其他類型以及更符合現場的裝配線平衡問題進行集成,并考慮成本、能耗和負載等多個目標。3 實驗分析
3.1 案例分析

3.2 有效性分析
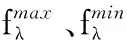

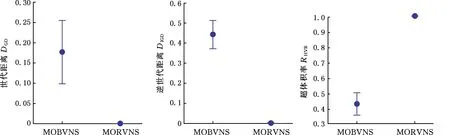
3.3 綜合性能分析

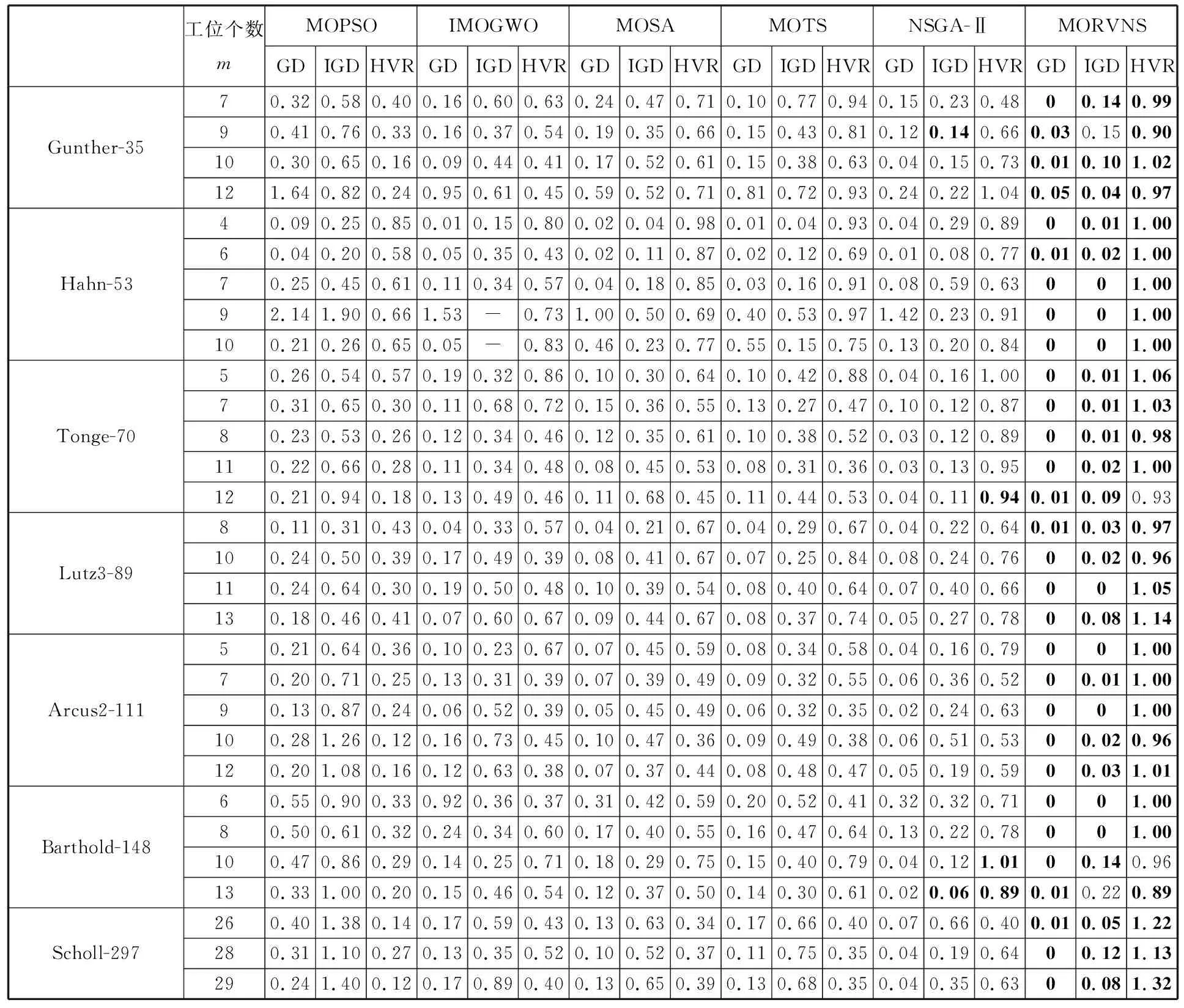

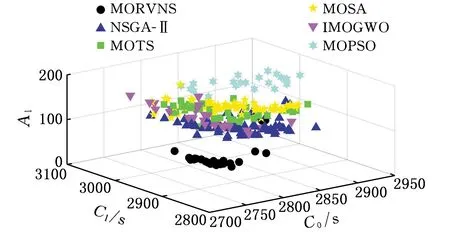
4 結論

