基于采蜜機制的正弦余弦算法及其在機械優化設計中的應用

王聯國 劉小娟

甘肅農業大學信息科學技術學院，蘭州，730070

0 引言

正弦余弦算法(sine cosine algorithm，SCA)[1]是一種基于正弦余弦函數模型的群體智能算法。該算法主要利用三角函數模型的周期振蕩性使其趨于問題的最優解，同時嵌入隨機參數和自適應參數，平衡算法的全局探索階段與局部開發階段。盡管SCA控制參數較少、模型簡單、易于實現、全局尋優能力強，但與其他智能優化算法一樣，在迭代后期仍易出現局部開發能力差、收斂速度慢和求解精度低等問題，致使算法陷入局部最優。

為了提高SCA的優化性能，國內外學者相繼以不同策略對SCA進行了改進。劉勇等[2]通過分析轉換參數，設計出了轉換參數拋物線函數遞減和指數函數遞減兩種正弦余弦算法，并以協同過濾推薦算法中相似度函數的計算為應用對象，驗證了改進指數函數遞減正弦余弦算法的可行性和有效性；徐明等[3]提出了一種基于非線性轉換參數和隨機差分變異策略的改進正弦余弦算法，并利用該算法優化神經網絡參數解決了兩類經典的分類問題；曲良東等[4]通過對正弦余弦算法進行簡化，提出了一種簡化的正弦余弦算法，仿真實驗結果表明新算法的搜索效率明顯高于基本正弦余弦算法；方旭陽等[5]通過引入精英反向學習策略及利用個體的反思學習能力，對正弦余弦算法進行改進，提高了算法的尋優精度，也避免了其未成熟收斂；郭文艷等[6]提出了一種基于精英混沌搜索策略的交替正弦余弦算法，增強了算法的探索能力，降低了算法時間復雜度，提高了算法收斂速度；李銀通等[7]提出了一種自學習策略和Lévy飛行的正弦余弦算法，提高了算法的優化性能；何慶等[8]提出了一種基于改進正弦余弦算法的節點部署優化方法，通過引入雙曲正弦調節因子、動態余弦波權重系數、拉普拉斯和高斯分布的變異策略，有效提高了無線傳感器網絡的性能；SHUBHAM等[9]提出了一種改進的全局優化正弦余弦算法，該算法主要將交叉的開發方案與個體解的最佳狀態相結合，同時將自學習與全局搜索機制相結合，增強了算法的開發能力，并減少了經典正弦余弦算法搜索方程中存在的多樣性溢出問題，最后通過圖像分割中的多閾值分割的仿真實驗，驗證了新算法解決實際優化問題的有效性；CHEN等[10]提出了一種用于求解全局優化和約束實際工程問題的多策略正弦余弦算法，將Cauchy突變算子、混沌局部搜索機制、基于反向學習策略等多種機制與基于差分進化的兩種算子相結合，有效避免了算法陷入局部最優；LALIT等[11]提出了一種混合二進制粒子群優化-正弦余弦算法(BPSO-SCA)特征選擇方法，仿真實驗表明該方法具有良好的性能。

上述改進算法通過調整參數、引入不同局部搜索策略或與其他智能算法相融合等策略，提高算法的優化性能，并且部分改進算法在求解實際復雜問題方面取得了較好的優化效果。然而，分析上述文獻發現，SCA與其他智能優化算法的混合模式研究成果相對較少，并且已有的研究成果在實際問題中的應用仍存在一定的局限性。

本文在已有SCA研究的基礎上，對縮短算法運行時間、參數位置調整、參數r1的自適應調整及r3的動態調整、與人工蜂群算法的采蜜機制融合、提高收斂速度、平衡全局探索與局部開發能力、防止算法陷入局部最優等方面進行了進一步的探索研究，提出了一種基于采蜜機制的正弦余弦算法(sine cosine algorithm based on the honey gathering mechanism，SCAHGM)。對23個標準測試函數和2個機械優化設計實例進行仿真實驗，驗證了SCAHGM的可行性、魯棒性和適用性。

1 標準正弦余弦算法

SCA求解優化問題始于一組隨機解，并通過全局探索和局部開發兩個階段逐步趨向全局最優解。假設優化問題的候選解對應搜索空間中個體的空間位置，則第i個個體的空間位置可表示為Xi=(Xi1，Xi2，…，XiD)T，i∈{1，2，…，N}，N為種群規模，D為搜索空間的維度，f(Xi)為第i個個體的目標函數值，P=(P1，P2，…，PD)T為種群中最優個體的空間位置。首先，在解搜索空間中按下式隨機初始化N個個體的空間位置：

(1)

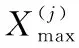
然后，在每一次迭代中，種群中第i個個體以均等概率選取正弦函數或余弦函數更新空間位置，其空間位置更新方程為：

(2)

由式(2)可見，r1、r2、r3和r4是SCA中起重要作用的4個參數。其中，參數r1決定下一次迭代時第i個個體的空間位置區域，它可在當前解與目標最優解間的區域或兩者所構成區域以外自由變化；參數r2定義了當前解朝目標最優解向內或向外移動的方向和步長；參數r3的作用是為目標最優解賦予一個隨機權重，以反映其所定義的搜索步長對目標最優解增強(r3>1)、減弱(r3<1)或保持(r3=1)的作用；參數r4的作用是以均等概率決定式(2)中正弦和余弦函數部分的迭代更新。隨機參數和線性遞減參數的設置使得算法能夠很好地平衡全局探索與局部開發能力[12]。

SCA能使全局探索和局部開發階段起到較好的平衡作用，以發現搜索空間中有希望的區域，并最終收斂到全局最優。在整個迭代過程起主要貢獻作用的是參數r1，并且r1是一個線性遞減函數，其值隨迭代次數的增加而線性減小，使用下式自適應地調整與變換式(2)中正弦與余弦的范圍：

(3)

式中，t為當前迭代次數；T為最大迭代次數；a為一個值為2的常數。

默認情況下，當迭代過程中滿足條件t>T時，算法終止優化過程。

圖1為正弦余弦算法的原理示意圖。在算法的整個迭代過程中，全局探索能力和局部開發能力的有機協調，體現出了種群個體在不同搜索空間的搜索行為。當正弦和余弦函數的范圍位于區間(1，2]和[-2，-1)之間時，SCA全局探索搜索空間；在區間[-1，1]之間時，局部開發搜索空間。

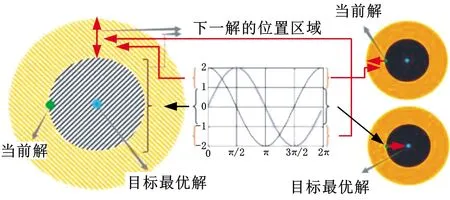
圖1 正弦余弦算法原理示意圖Fig.1 Principle diagram of SCA

2 基于采蜜機制的正弦余弦算法

2.1 改進算法的思路策略

2.1.1每個個體采用相同的參數r1、r2、r3和r4

由于SCA在一次迭代中，r1本身是采用統一的計算公式，即所有個體都采用相同的r1，因此，將SCA中參數r2、r3和r4的位置從每個個體的維度循環內改為維度循環外，使每個個體采用相同的參數r1、r2、r3和r4，并使每個個體的所有維度以相同方式與比例進行搜索，提高算法的搜索效率。

2.1.2按冪遞減函數自適應調整參數r1

文獻[2]將參數r1改為指數遞減函數，分析了參數r1對算法性能的影響。本文調整參數r1為冪遞減函數，表達式如下：

(4)

式中，s為調整參數，主要作用是調整非線性冪遞減函數的下降速率。

圖2反映了算法在最大迭代次數為1000時參數r1按線性遞減函數[1]、指數遞減函數[2]和冪遞減函數變化的趨勢。從圖2可以看出，在算法的整個迭代過程中，線性遞減函數曲線是勻速下降的。相比線性遞減函數曲線，指數遞減函數曲線隨著迭代次數的增加，r1逐漸變小，與線性遞減函數曲線下降規律相似，體現出算法全局探索能力和局部開發能力的有機協調。冪遞減函數曲線與線性遞減函數曲線下降規律不同，在前期迭代次數小，r1較大，當迭代次數大于500時，曲線出現轉折，之后執行算法的局部開發階段，中后期隨著迭代次數的持續增加，r1非線性遞減，逐漸為0，體現出算法在前期全局探索能力最強，到中后期局部開發能力增強。

圖2 參數r1遞減曲線對比圖Fig.2 Comparison chart of decline curve of parameter r1

由于標準SCA中正余弦算子具有優異的全局探索能力，但局部開發能力較弱，因此本文調整參數r1為冪遞減函數以更好地平衡算法的全局探索能力和局部開發能力。

2.1.3動態調整參數r3

參數r3反映其所定義的搜索步長對目標最優解增強(r3>1)、減弱(r3<1)或保持(r3=1)的作用。算法前期，r3在[0，2]之間隨機取值，有利于算法的全局搜索，但到中后期既要注重算法的全局探索能力，更要加強算法的局部開發能力，同時要發揮目標最優解對優化過程的實際引導作用，提高算法的優化精度，因此，在算法中后期，r3以一定概率取常數1，減少隨機性，加快算法的搜索速度。參數r3的調整策略如下：

(5)

式中，ξ、Ψ分別為[0，1]之間的常數；R2、R3分別為(0，1)和[0，2]之間的隨機數。

2.1.4貪婪選擇策略

貪婪選擇通用于所有的智能優化算法，該策略通過保留種群中的精英個體，使算法進化方向恒定，促使算法盡快找到全局最優解。根據個體i的空間位置Xi和按更新策略產生的新個體空間位置Vi的函數值f(·)，選擇較優個體進入下一代。對于最小化問題，其選擇策略按下式進行：

(6)

同時按照下式更新連續停留次數n：

(7)

2.1.5蜂群采蜜機制

人工蜂群(artificial bee colony，ABC)算法是土耳其學者DERVIS等[13]于2005年受蜜蜂行為啟發提出的一種覓食尋優算法。ABC算法利用不同類型蜜蜂(采蜜蜂、觀察蜂和偵察蜂)的分工協作機制求解問題的最優解，主要包括種群初始化、采蜜蜂、觀察蜂和偵察蜂四個階段。本文利用ABC算法中的采蜜蜂算子增強SCA的局部開發能力，提高算法的優化精度。在迭代過程中，以一定概率交替執行正余弦算子或采蜜蜂算子，同時利用偵察蜂算子防止算法陷入局部極值，提高全局探索能力，較好地平衡SCA的全局探索和局部開發階段。

(1)采蜜蜂算子。采蜜蜂算子具有較強的局部開發能力，采蜜蜂根據下式進行鄰域搜索并產生新蜜源，同時計算新蜜源的適應度函數值，再采用貪婪選擇策略或輪盤賭法更新蜜源：

Vij=Xij+R4(Xij-Xkj)

(8)

式中，Vij為新產生的蜜源位置；R4為[-1，1]之間的隨機數；j和k隨機選取，j∈{1，2，…，D}，k∈{1，2，…，N}，且k≠i，N為蜜蜂總數。

(2)偵察蜂算子。偵察蜂算子主要搜尋在蜂巢周圍潛在的蜜源。當連續停留次數n達到一定的閾值L仍未找到更優空間位置時，即表明陷入了局部最優，此時蜜蜂的角色由采蜜蜂或觀察蜂轉變為偵察蜂，并按照式(1)重新搜索隨機產生新蜜源。

2.1.6更改空間位置更新方程

因正弦函數sinr2取正值和負值的概率相等，文獻[4]去掉式(2)中的絕對值符號，故本文引入該方法并將空間位置更新方程改寫為

(9)

2.2 改進算法的具體步驟

SCAHGM的具體步驟如下：

(1)初始化參數，如種群規模N、空間維度D、閾值L、當前迭代次數t、最大迭代次數T、目標精度O及常數a等，隨機產生初始種群；

(2)計算種群中每個個體的函數值，并記錄全局最優解；

(3)按照概率P執行正余弦算子階段，按照概率1-P執行采蜜蜂算子階段，若執行正余弦算子階段，轉向步驟(4)，否則，執行采蜜蜂算子階段，并轉向步驟(5)；

(4)在正余弦算子階段，隨機產生參數r2和r4，并根據式(4)、式(5)計算參數r1和r3的值，隨后再以式(9)更新每個個體的空間位置，轉向步驟(6)；

(5)在采蜜蜂算子階段，根據式(8)產生新蜜源；

(6)計算每個個體的函數值；

(7)執行貪婪選擇策略，按照式(6)更新每個個體，按照式(7)更新連續停留次數n；

(8)更新全局最優解；

(9)執行偵察蜂算子，若連續停留次數n達到閾值L，則采蜜蜂變為偵察蜂，按照式(1)隨機產生新蜜源；

(10)判斷是否達到算法設定的收斂條件(如最大迭代次數T或目標精度O)，若是，停止迭代并輸出最優值，否則轉向步驟(3)。

2.3 改進算法的時間復雜度分析

SCAHGM的時間復雜度主要由標準SCA、采蜜蜂算子和偵察蜂算子三部分組成，并按照概率P執行正余弦算子階段，按照概率1-P執行采蜜蜂算子階段。假設種群規模為N，問題維度為D，最大迭代次數為T，則正余弦算子的時間復雜度為O1(NPDT)，采蜜蜂算子的時間復雜度為O2(N(1-P)T)，偵察蜂算子的最大時間復雜度為O3(NDT/L)，則SCAHGM的時間復雜度為

O(SCAHGM)=O1(NPDT)+O2(N(1-P)T)+

O3(NDT/L)

(10)

標準SCA的時間復雜度為

O4(SCA)=O5(NDT)

(11)

3 仿真實驗與分析

3.1 測試函數及參數設置

以求23個標準測試函數的最小值為例進行仿真實驗，客觀評價SCAHGM的優化性能，函數表達式詳見文獻[1，14]，其他參數及目標精度如表1所示。其中，f1～f7為單峰函數，在定義域內只有一個極值，用于測試算法的收斂速度和尋優精度，并考察算法的優化性能；f8～f13為多峰函數，f14～f23為固定維度多峰函數，由于這些函數較復雜，存在多個極值點，因而算法尋找全局最優值的難度較大，常用于測試算法全局探索與避免早熟的能力。

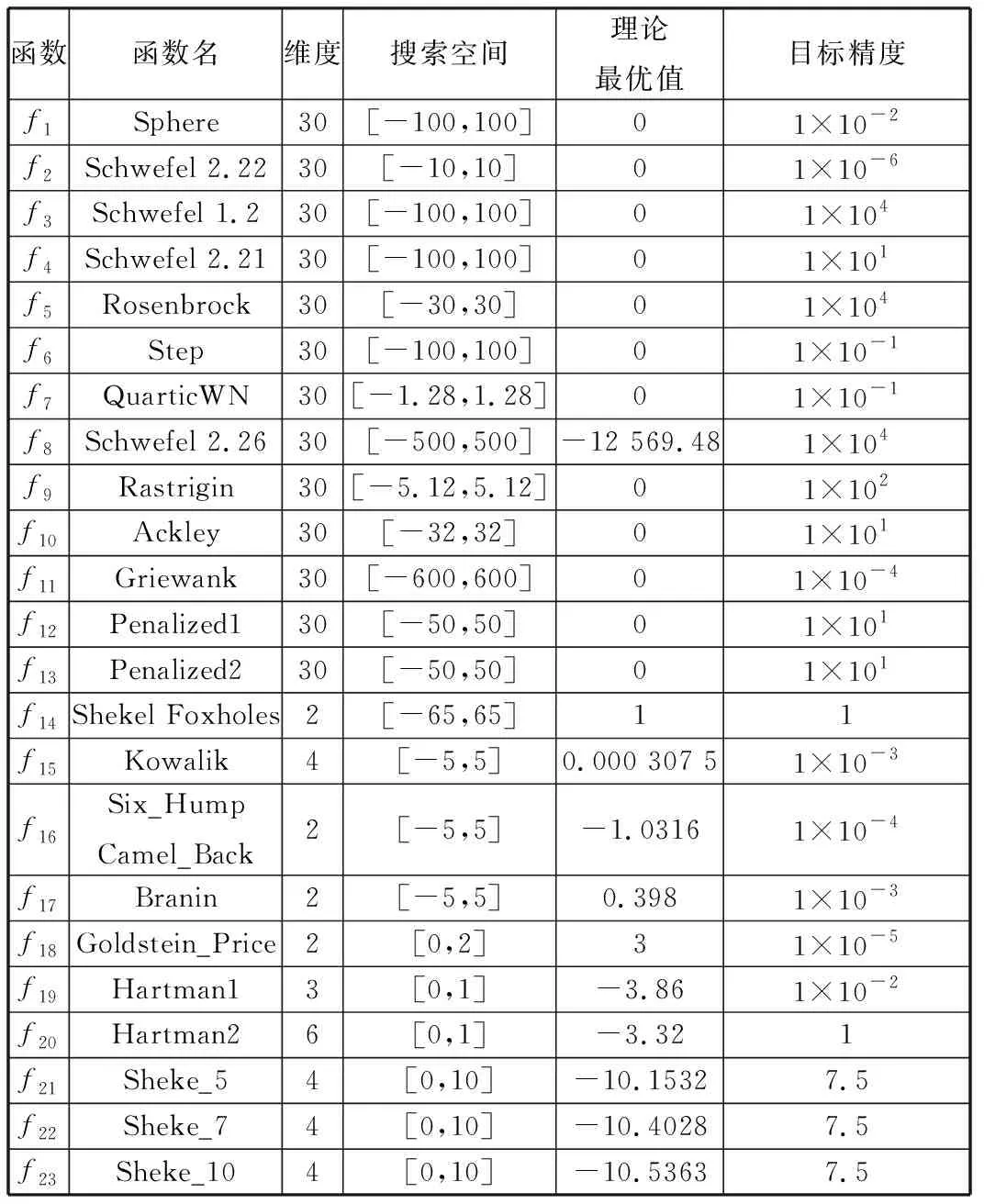
表1 23個標準測試函數參數表Tab.1 Parameters of 23 standard benchmark functions

3.2 SCAHGM與標準SCA的性能比較

為了測試SCAHGM的性能，本文將其與標準SCA在種群規模一定，維度和最大迭代次數變化的條件下進行比較。實驗中兩種算法參數設置為：在單峰函數f1～f7和多峰函數f8～f13中，種群規模N=30，維度D為30、50、100，對應的最大迭代次數T為1000、2000、3000；在固定維度多峰函數f14～f23中，種群規模N=30，最大迭代次數T=1000。即，為了公平起見，兩種算法采用相同的函數最大評價次數M(M=NT)。此外，經實驗驗證，當閾值L=140、式(4)中的s=5、式(5)中的ξ=0.5和Ψ=0.6以及根據式(2)中參數r4的范圍所確定步驟(3)中概率P=0.5時，SCAHGM優化效果較好。兩種算法獨立運行30次的實驗結果見表2，其中，加粗數據代表對比結果的最優值，下同。圖3～圖8列出了N=30，T=1000的部分測試函數收斂曲線。其中，平均最優值反映算法的收斂速度和求解精度，標準差反映算法的穩定性和魯棒性，最大值和最小值反映可行解的質量，成功率反映算法達到目標精度的執行效率，平均運行時間反映算法運行的時間成本，收斂曲線圖反映算法的收斂趨勢變化。

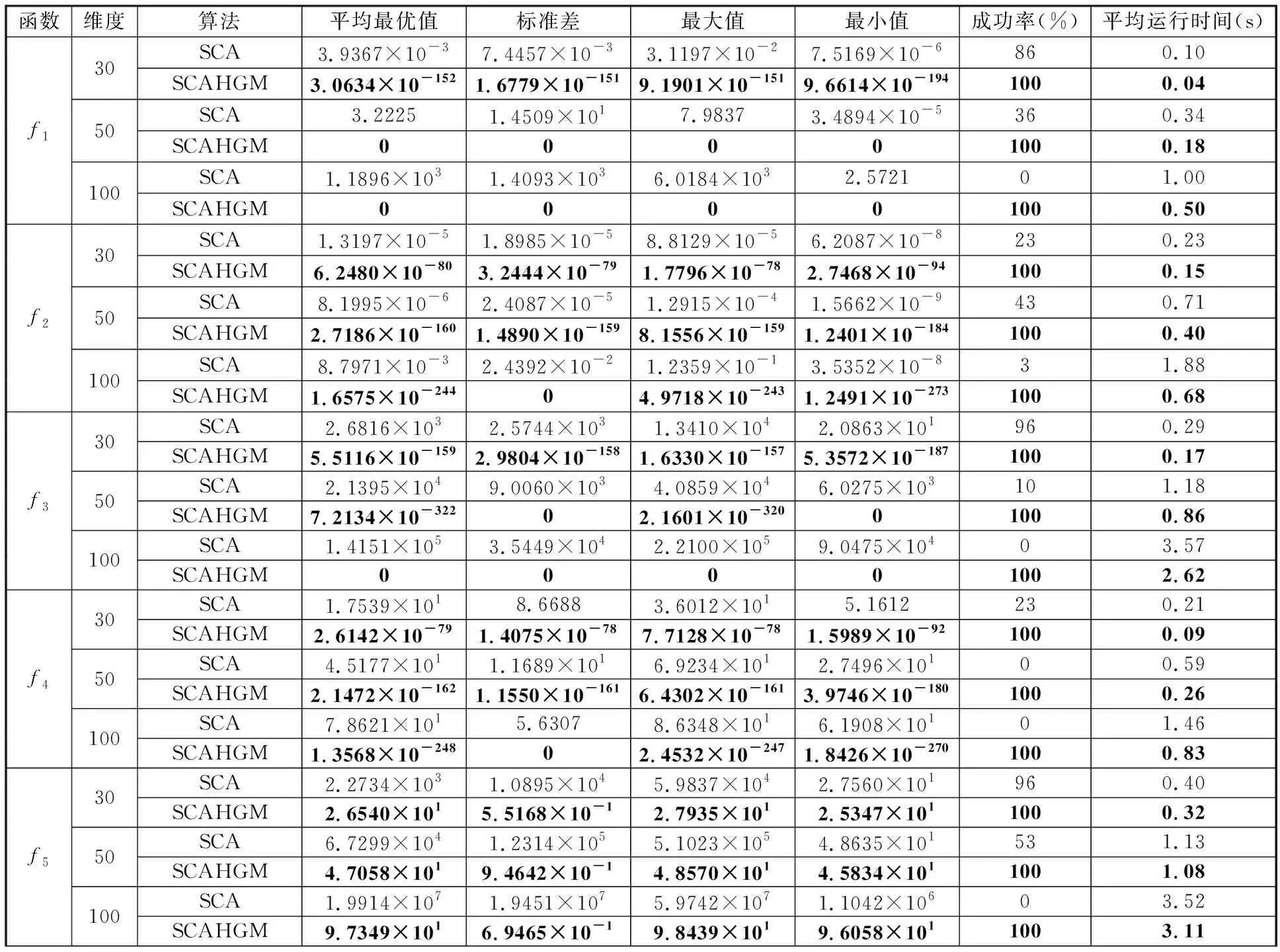
表2 SCAHGM與標準SCA的實驗結果Tab.2 Experiment results of SCAHGM and standard SCA

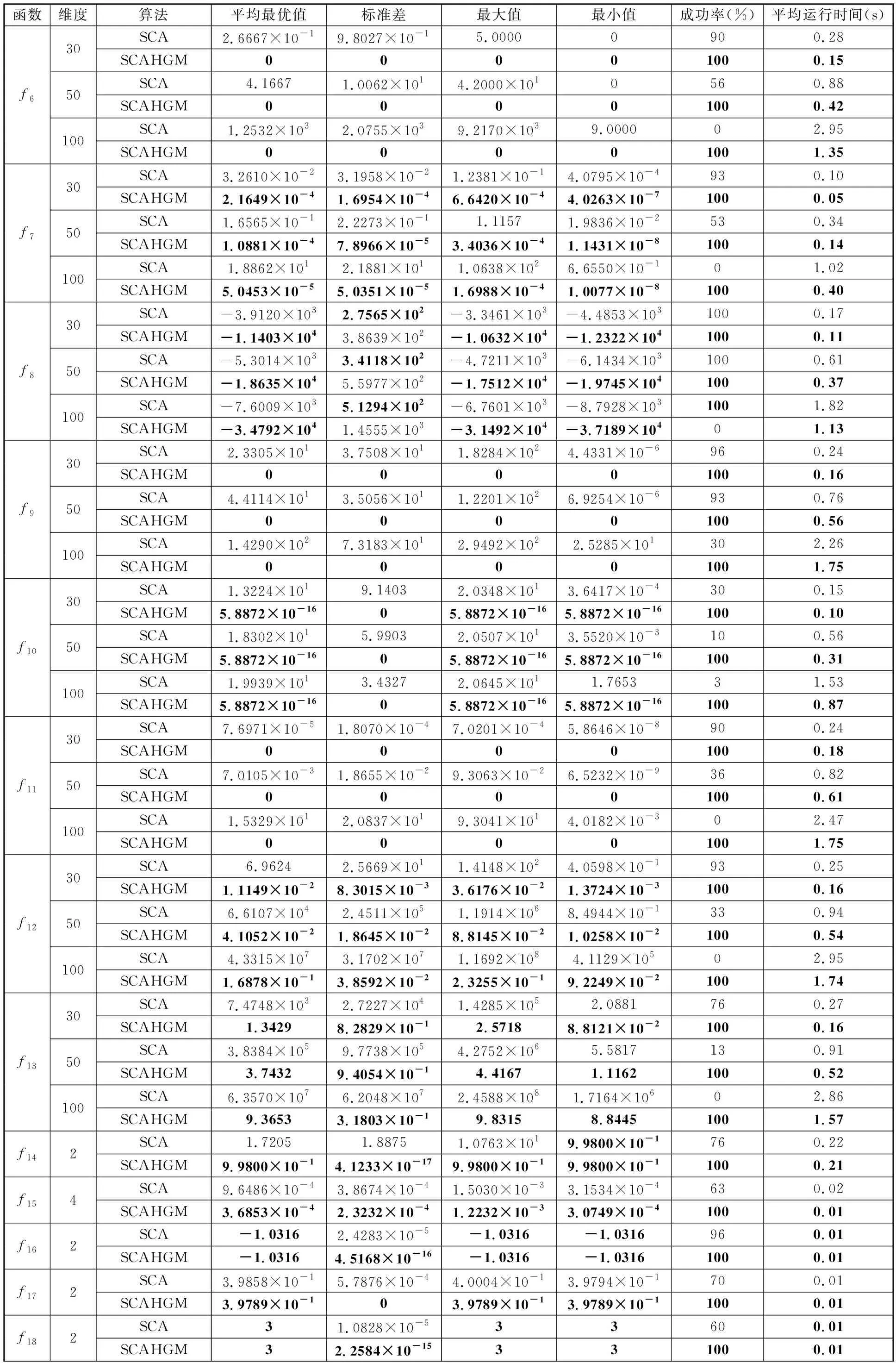
續表

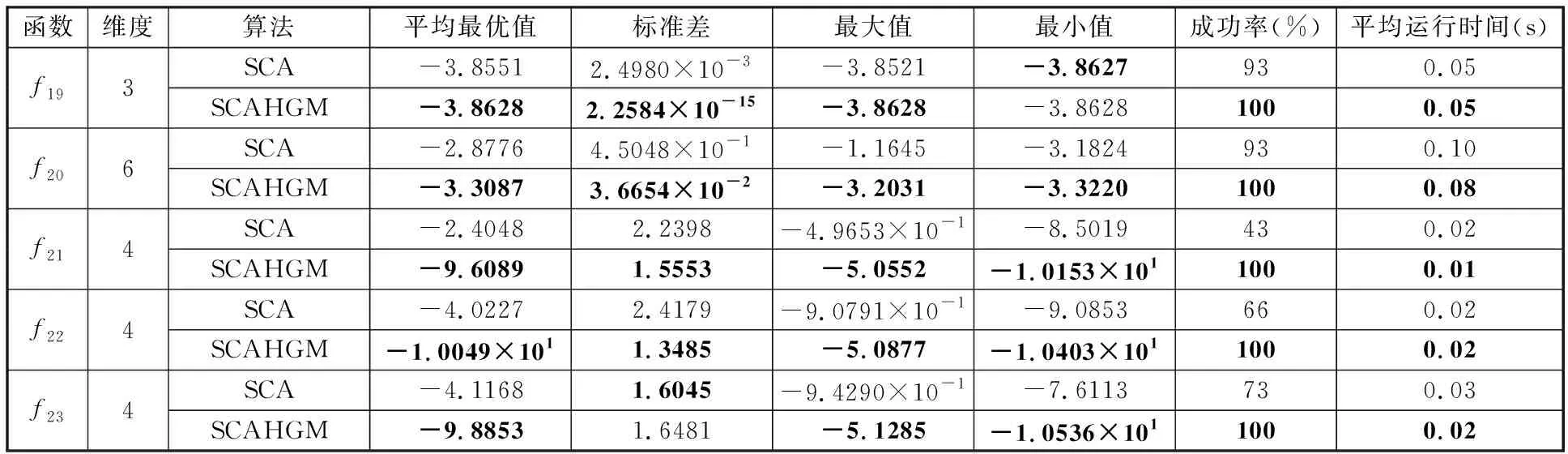
續表

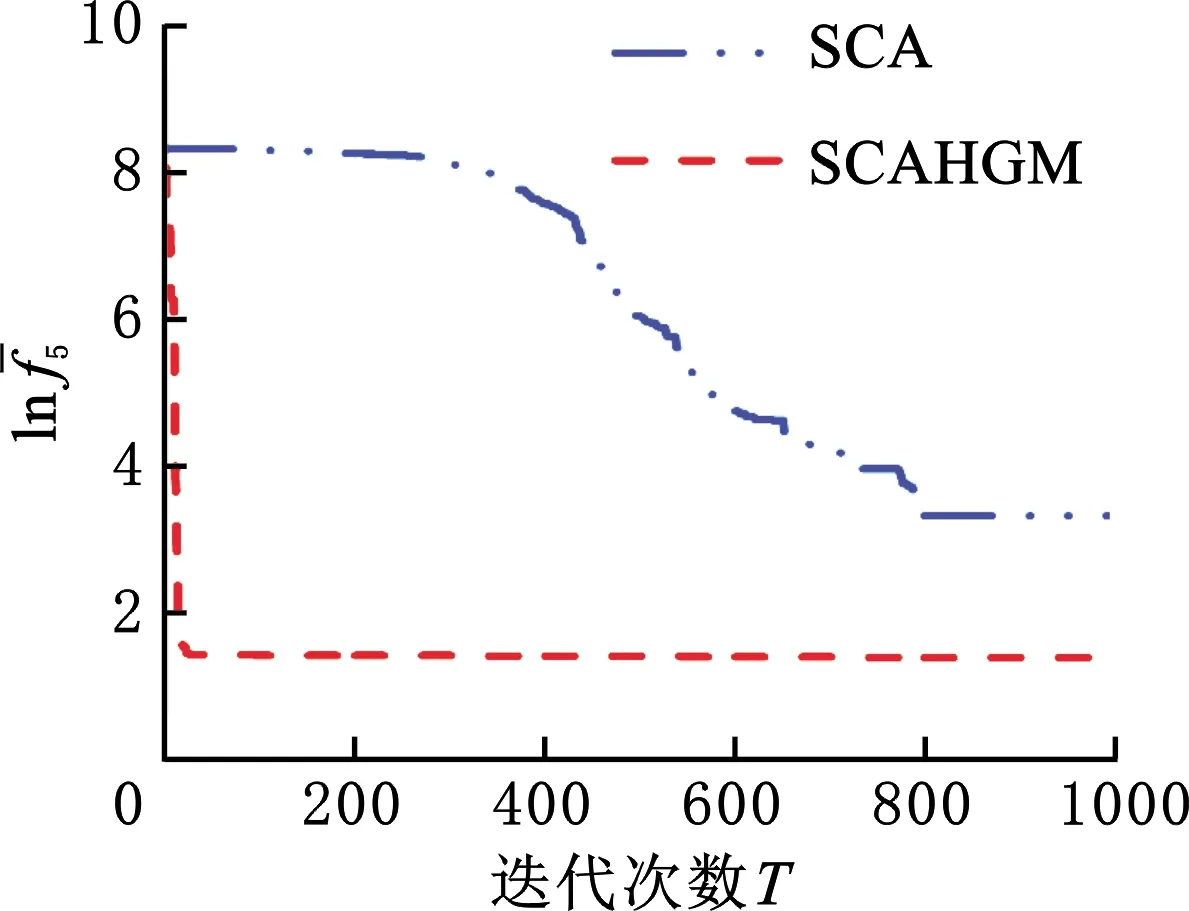
圖3 f5平均最優值的收斂曲線Fig.3 Convergence curve of the average optimal value of f5

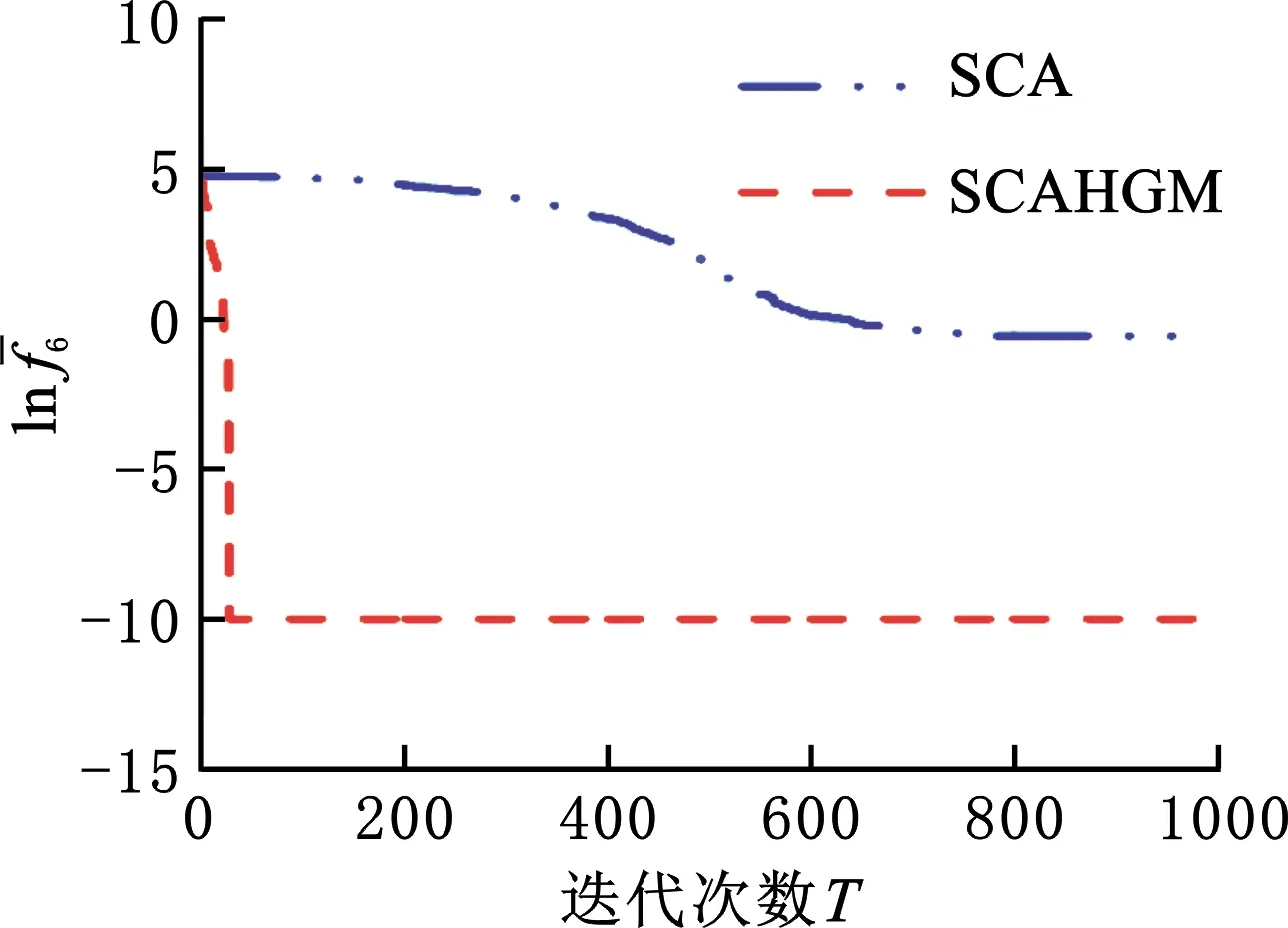
圖4 f6平均最優值的收斂曲線Fig.4 Convergence curve of the average optimal value of f6

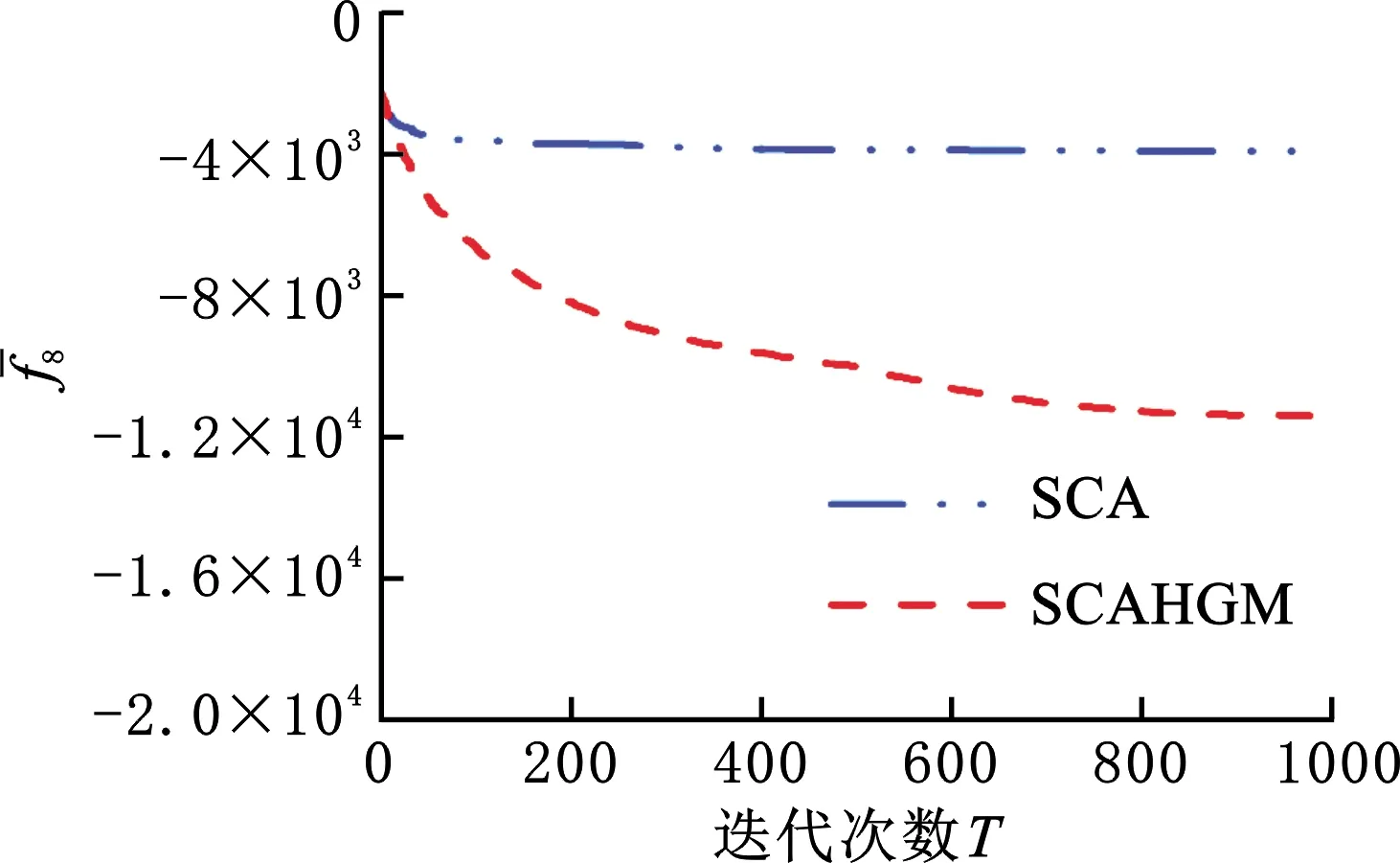
圖5 f8平均最優值的收斂曲線Fig.5 Convergence curve of the average optimal value of f8

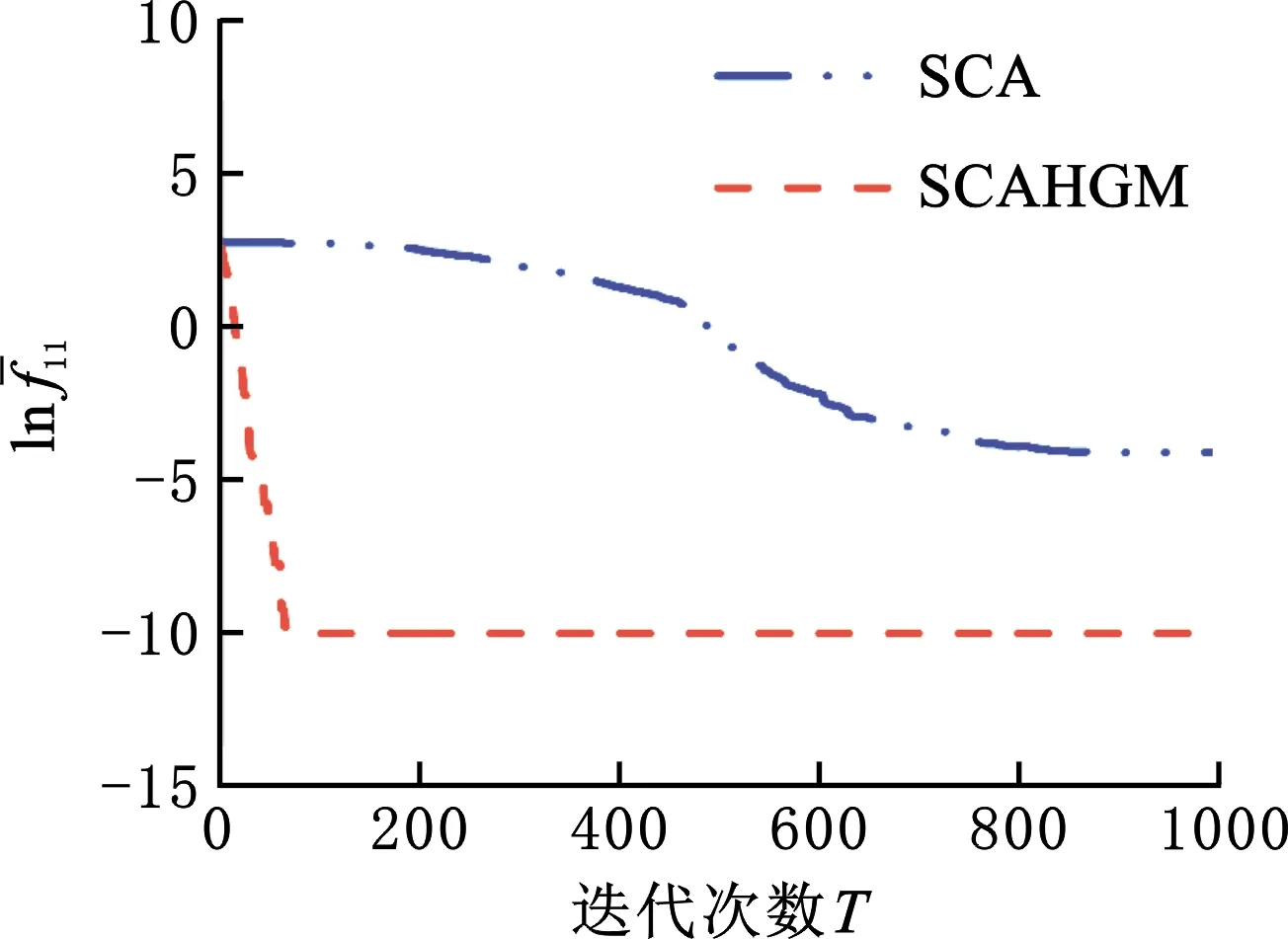
圖6 f11平均最優值的收斂曲線Fig.6 Convergence curve of the average optimal value of f11

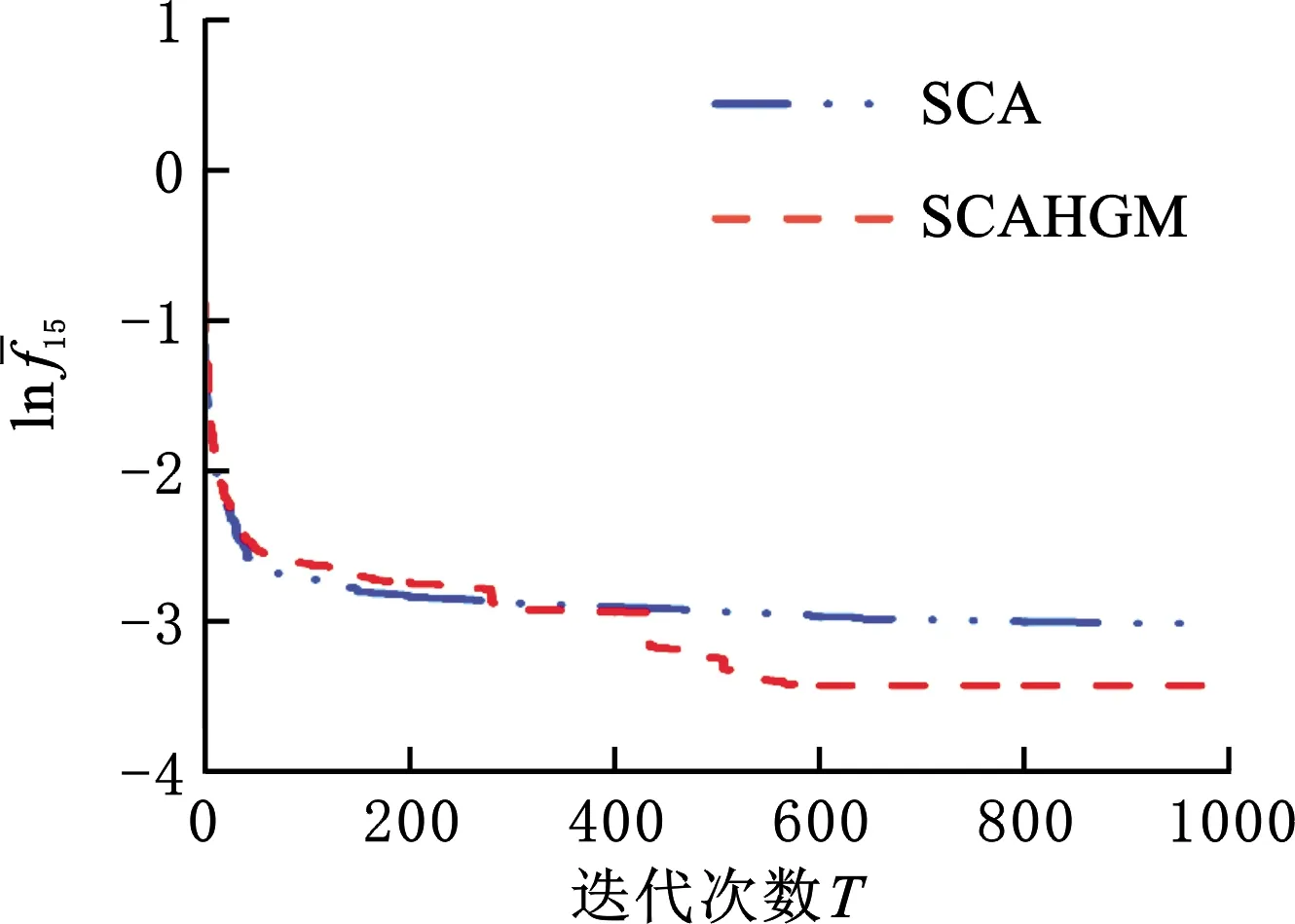
圖7 f15平均最優值的收斂曲線Fig.7 Convergence curve of the average optimal value of f15

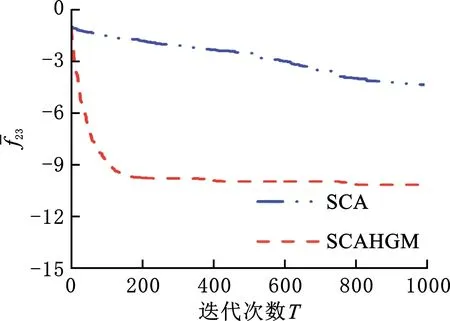
圖8 f23平均最優值的收斂曲線Fig.8 Convergence curve of the average optimal value of f23

從不同峰型的測試函數在平均最優值、標準差、成功率和平均運行時間四方面的優化效果來看：在f1～f7單峰函數中，SCAHGM在四方面均達到了顯著的優化效果。其中，f5(Rosenbrock)被稱為“病態函數”，是一個對大部分優化函數都難以收斂到全局最優的極復雜單峰函數，而SCAHGM卻能得到較好解，這說明SCAHGM較好地克服了SCA的缺陷；在f8～f13的多峰函數中，對尋優難度較大的f8，SCAHGM在維度D為30，50，100下的穩定性不如SCA。然而，對具有許多局部極小值的函數f10和多模態函數f12、f13，SCAHGM均達到了一定數量級的明顯優化效果，并且在具有強烈振蕩的復雜多模態函數f9和f11中，也已取得了理論最優值；在f14～f23的固定維度多峰函數中，SCAHGM均表現出較好的優化能力。在所有測試函數的對比結果中，SCAHGM平均運行時間變短，這是由于在局部開發能力較強的采蜜蜂算子中，每個個體只更新一個維度的數據，再結合全局探索能力強的正余弦算子，運算速度加快，時間變短。

收斂曲線圖中，除了圖5和圖8外，其余曲線圖的縱坐標為函數平均最優值的對數值，橫坐標為迭代次數。另外，圖4和圖6均以10-10作為截止值，避免函數值變為0致使曲線中斷。

分析收斂曲線圖發現，對f8和f23而言，SCAHGM分別約在500和150次時開始收斂，并隨著迭代次數增加持續收斂；對f5、f6和f11而言，SCAHGM一開始就表現出顯著的收斂速度，迭代次數不到100次時已收斂；對于SCAHGM，f15在前期收斂速度和精度稍遜于SCA，但當迭代次數在400次以后，其收斂速度加快并取得更高的收斂精度。總體上看，SCAHGM的收斂速度和精度都有顯著的改進效果。

為驗證以上實驗結果的真實性并更好地評估算法性能，采用顯著性水平為5%的Wilcoxon signed ranks檢驗進行測試。表3給出了SCAHGM與標準SCA的Wilcoxon signed ranks統計決策結果。其中，“+”表示SCAHGM優于SCA，“-”表示SCAHGM遜于SCA，“=”表示兩者作用相當。

表3 顯著性水平為0.05的Wilcoxon signed ranks統計決策Tab.3 Statistical decision based on Wilcoxon signed ranks

表3中決策結果顯示，23個測試函數的所有顯著性pvalue均小于0.05，并且決策結果均顯示為“+”，這說明了SCAHGM的有效性，也表明SCAHGM較標準SCA具有顯著的優化效果。

以上分析表明，改進SCAHGM具有更好的收斂效果、更高的優化精度、較強的魯棒性和較小的時間代價，從而驗證了算法的優越性。

3.3 SCAHGM與SCA改進算法及其他元啟發式算法的性能比較

為進一步測試SCAHGM的性能，將其與SCA的改進算法及近年來提出的其他元啟發式算法進行比較。

(1)將SCAHGM與SCA改進算法OBSCA[15]、COSCA[6]、m-SCA[16]、ESCA[2]、MSCA[17]進行比較。為體現公平性，SCAHGM和其他SCA改進算法采用相同的參數設置，并使算法的函數最大評價次數保持一致。除了ESCA 和SCAHGM外，其他算法的實驗數據取自各文獻。表4列出了SCAHGM與幾種SCA改進算法的性能比較結果，其中，Ave表示平均值，Std表示標準差。由表4可以看出，在SCAHGM與OBSCA、COSCA、m-SCA三者的比較實驗中(函數最大評價次數M=15 000)，SCAHGM相對于OBSCA，除了測試函數f7的優化效果稍遜于OBCSA外，其余測試函數的優化效果均優于OBSCA；SCAHGM相對于COSCA，除了測試函數f2、f21、f22和f23的優化效果稍遜于COSCA外，SCAHGM對其他19個測試函數的優化效果優于COSCA；SCAHGM相對于m-SCA，除了測試函數f13和f16的優化效果稍遜于m-SCA外，SCAHGM對其他21個測試函數的優化效果相對較好；在SCAHGM與ESCA比較實驗中(M=300 000)，SCAHGM相對于ESCA，除了測試函數f7的優化效果遜于ECSA外，在其他22個測試函數上的優化效果仍然相對較好；在SCAHGM與MSCA比較實驗中(M=500 000)，SCAHGM相對于MSCA，除了測試函數f1～f4、f6、f9、f11、f14和f16的優化效果與MSCA相當，f5、f8、f12、f13和f15的優化效果遜于MSCA外，在其他6個測試函數上的優化效果仍然相對較好(測試函數f21～f23在文獻[17]中無實驗數據)。

(2)將SCAHGM與其他元啟發式算法[18]及HPSO[19]進行比較。將SCAHGM、HPSO及文獻[18]中的7種算法的參數設置相同，即所有算法的函數最大評價次數仍保持一致。除SCAHGM和HPSO進行仿真實驗外，其余對比算法的實驗數據來自文獻[18]，表5列出了SCAHGM與其他元啟發式算法的性能比較結果(表中僅列出了算法運行30次后取得的平均最優值)。

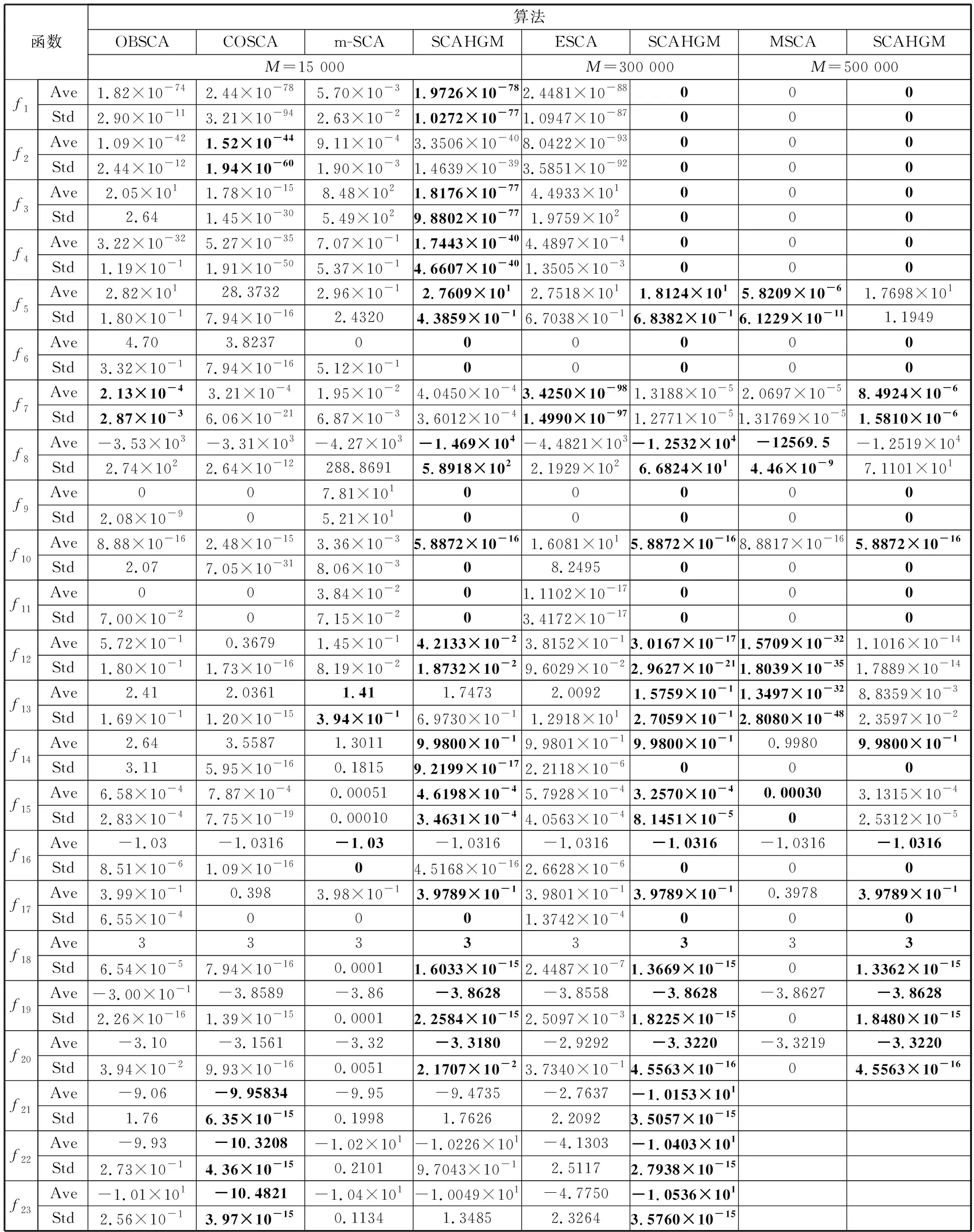
表4 SCAHGM與SCA改進算法的性能比較Tab.4 Performance comparison of SCAHGM with the improved algorithms for SCA

表5結果顯示，相比其他8種對比算法，除了測試函數f7、f12、f13、f16和f17外，SCAHGM對其他18個測試函數都能得到最好的優化結果，表現出了相對顯著的優化性能。

綜上所述，基于采蜜機制的正弦余弦算法求解精度高、魯棒性強、收斂性好，取得了相對較好的優化效果，提高了算法的優化效率。

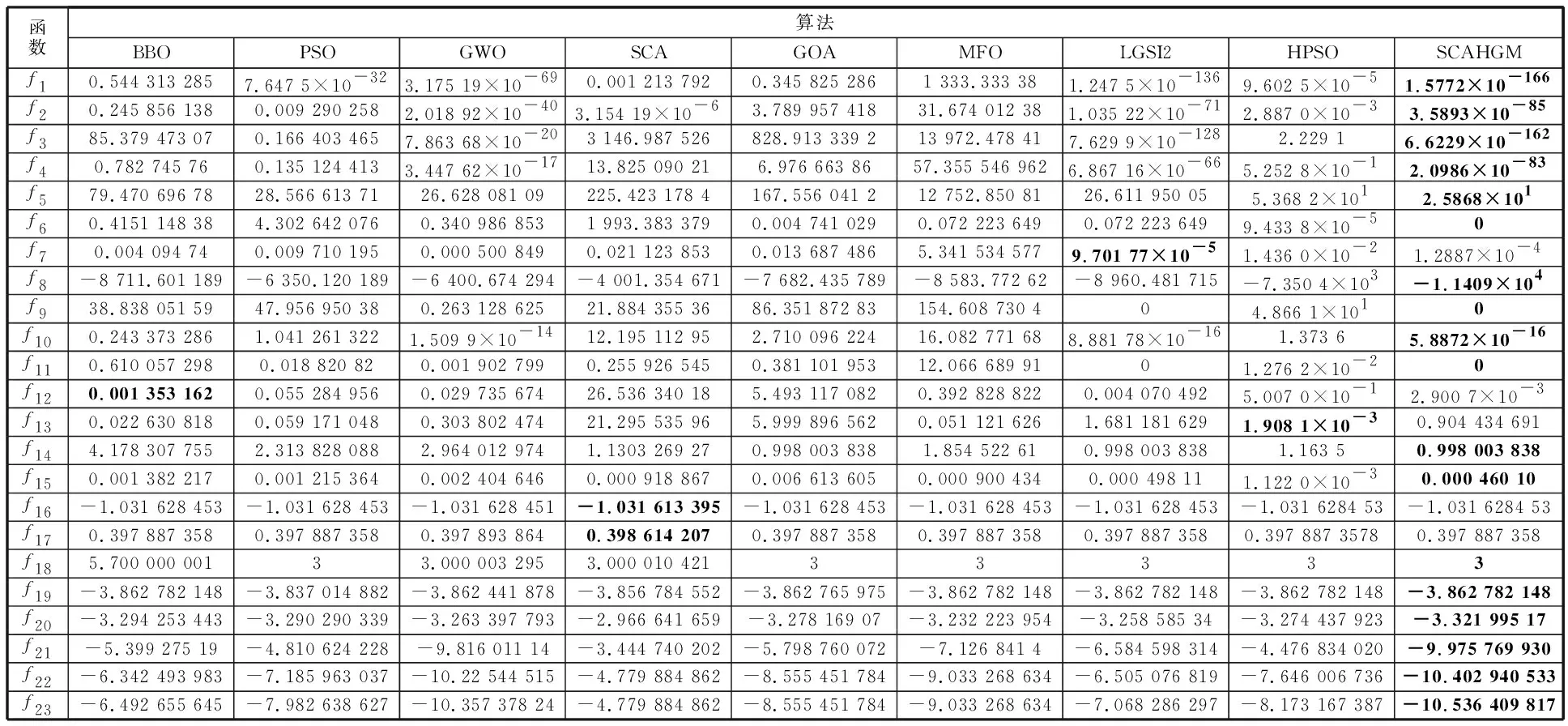
表5 SCAHGM與其他元啟發式算法的性能比較Tab.5 Performance comparison of SCAHGM with other meta-heuristic algorithms

4 應用

本文將提出的SCAHGM用于求解機械優化設計問題，以說明提出算法的可行性和適用性。

4.1 機械優化設計問題的數學模型

選取設計變量、列出目標函數、給定約束條件是構造優化設計問題數學模型的重要步驟。該問題的數學模型一般可以描述為如下約束非線性優化設計問題[20]：

(12)

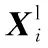
4.2 約束優化問題的處理方法

群體智能優化算法求解約束優化問題時需要將約束問題轉化為無約束優化問題進行求解。將約束優化問題轉化為無約束優化問題的主要處理方法是罰函數法[21]。該方法的基本思想是：構造懲罰項并將其加入目標函數中以構成懲罰函數，使約束優化問題轉化為求解一系列無約束極值子問題，然后按照無約束優化方法來求解。該策略將對求解過程中違反約束條件的迭代點進行“懲罰”，進而迫使無約束子問題的極小值點趨向于滿足約束條件[22]。

基于此，罰函數的一般形式為

F(X)=f(X)+λ(h2(X)+[min(0，g(X))]2)

(13)

式中，F(X)為懲罰函數；f(X)為優化問題的原始目標函數；λ為懲罰因子；h2(X)和[min(0，g(X))]2分別為與等式有關的懲罰項和與不等式有關的懲罰項。

4.3 設計實例及仿真實驗

利用SCAHGM優化2個機械設計問題，通過計算機仿真來驗證所提出算法的性能。實例1來自文獻[16]，實例2來自文獻[19]。為了體現比較的公平性，SCAHGM與其他算法作對比時，實例1和實例2中SCAHGM參數設置分別為：N=50，T=2500和N=30，T=2700。另外，因實例均受約束限制，SCAHGM采用罰函數法處理約束越界。算法獨立運行30次并取最優值，具體實驗結果如表6～表8所示。

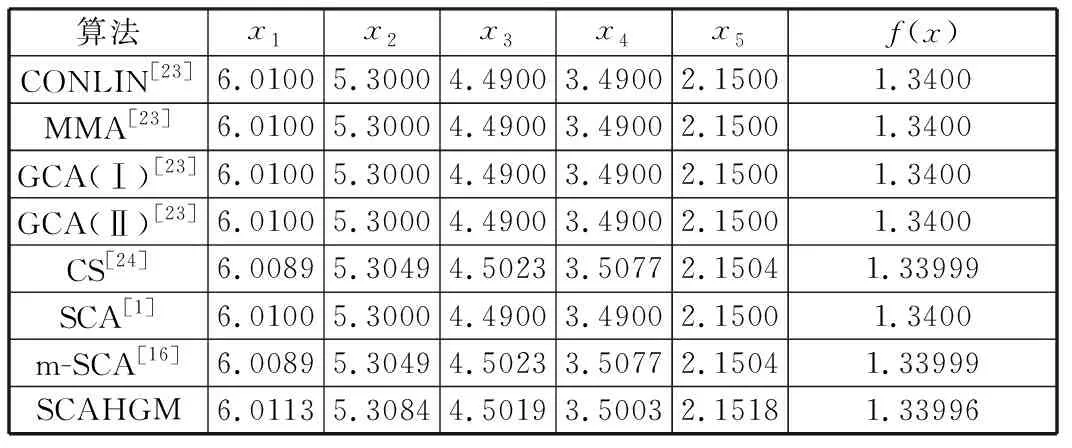
表6 不同算法對實例1的最優解比較Tab.6 Comparisons of the optimal solution for example 1

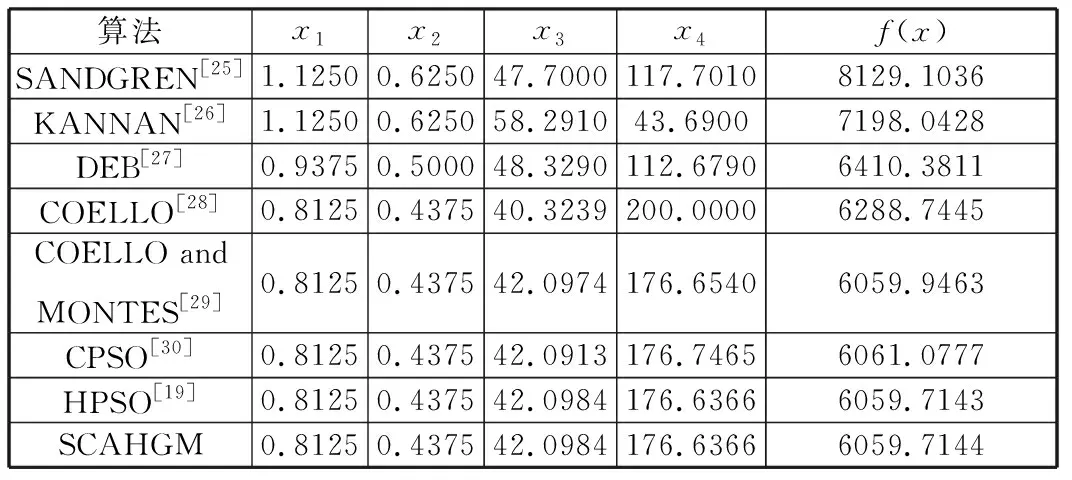
表7 不同算法對實例2的最優解比較Tab.7 Comparisons of the optimal solution for example 2

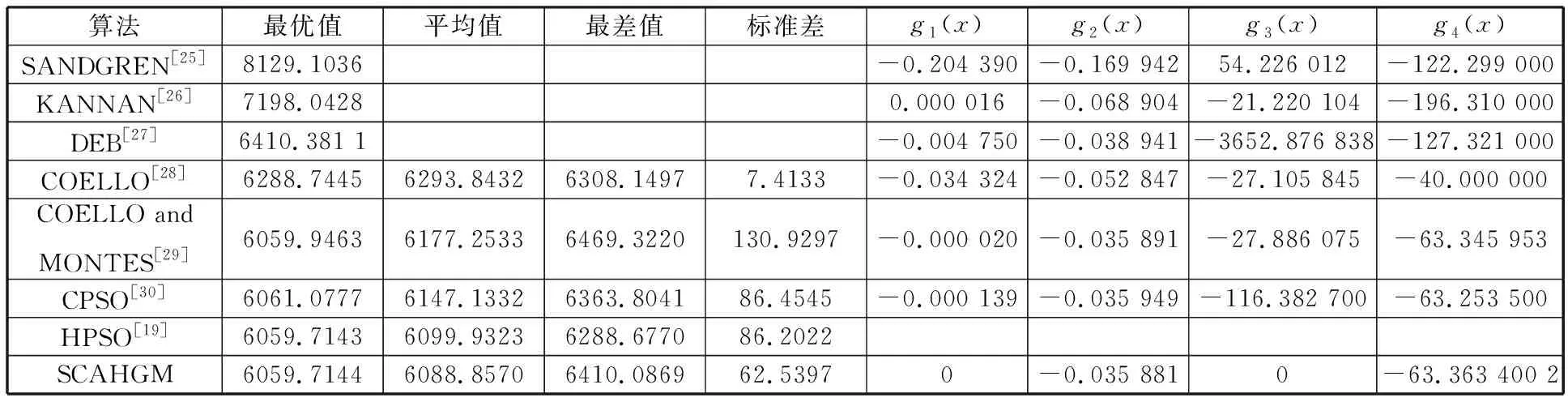
表8 不同算法求解實例2的統計結果Tab.8 Statistical results of the optimal solution for example 2 by different algorithms

4.3.1懸臂梁設計問題

根據懸臂梁平面結構[16]，該問題受不同單元梁高度(或寬度)約束，設計目標為使懸臂梁矩形截面的質量盡可能小。其數學模型如下：

(14)

式中，f(x)為最小化懸臂梁矩形截面的質量；設計變量

xi表示不同單元梁的高度(或寬度)。

文獻[1，16，23-24]給出了該實例的解，表6所示是SCAHGM與其他文獻獲得最優解的比較結果。可以明顯地看出，SCAHGM獲得的最優解要優于其他文獻中算法的最優解。

4.3.2壓力管道設計問題

根據壓力管道平面結構[19]，該問題的設計目標為最小化費用總成本，包括材料、成形和焊接的成本。其數學模型如下：

(15)

式中，f(x)為最小化費用總成本；四個設計變量x1，x2，x3和x4分別表示殼體厚度、頭部厚度、內半徑和除頭部外的圓柱形截面長度，x1和x2必須為1.5875 mm(0.0625 in)的整數倍，x3和x4為連續變量。

文獻[19，25-30]給出了該實例的解，表7所示是SCAHGM與其他文獻獲得最優解的比較結果，表8給出了不同算法求解實例2獲得最優值統計結果的比較(表中g1(x)～g4(x)部分的數據來自文獻[30])。

由表7可見，SCAHGM的最優解與HPSO的最優解相當，且優于其他算法的最優解。同時，在表8的統計結果中，除了文獻[28]外，SCAHGM的平均值和標準差小于對比算法的平均值和標準差，這表明SCAHGM的平均搜索能力優于其他算法，具有較好的收斂精度和較強的魯棒性。此外，根據表8所列的其他算法求解函數值和SCAHGM處理的約束函數值，SCAHGM獲得的函數最優解為(x1，x2，x3，x4)=(0.81250，0.437 50，42.098 445 595 854 919，176.636 599 813 031 040)，最優值f(x)=6 059.714 427 88，約束函數g1(x)=0，g2(x)=-0.035 880 829 015 544 069，g3(x)=0，g4(x)=-63.363 400 186 968 960 000，均滿足約束條件。

4.4 求解機械優化設計實例小結

(1)通過懸臂梁設計和壓力管道設計問題的實例驗證，本文算法SCAHGM可以取得優于或相近于其他文獻算法的優化結果，說明SCAHGM優化機械設計問題是可行有效的。

(2)由于機械優化設計問題的數學模型具有一定的通用性，故其他工程優化設計問題均可表示為式(12)描述的約束非線性優化設計問題，通過罰函數法轉化為無約束優化問題，再用改進算法SCAHGM求解，表明SCAHGM具有一定的實際應用可行性。

5 結論

(1)更改標準正弦余弦算法(SCA)中參數的位置，使每個個體采用相同的參數r1、r2、r3和r4，并按冪遞減函數非線性調整參數r1，動態調整參數r3，減少隨機性，提高了算法的搜索效率。

(2)利用智能算法通用的貪婪選擇策略，加快了算法的收斂速度，并協同偵察蜂算子，提高了種群多樣性，防止算法陷入局部最優。

(3)按一定概率交替執行正余弦算子或采蜜蜂算子，更好地平衡算法的全局探索與局部開發能力，有效彌補了算法局部開發能力差的不足。

(4)選取23個標準測試函數進行仿真實驗，將基于采蜜機制的正弦余弦算法(SCAHGM)與標準SCA、改進SCA和其他元啟發式算法進行比較，結果表明提出的SCAHGM具有較好的尋優性能。

(5)通過優化2個機械設計實例，驗證了SCAHGM的可行性和適用性，為解決工程設計優化問題提供了一條新途徑。