彈塑性狀態下扭轉中心移動分析*

田志昌，王彪

(內蒙古科技大學 土木工程學院，內蒙古 包頭 014010)

1 結構側移剛度

若一幢建筑質量分布的中心軸與結構抗扭中心軸重合，則抗震中結構不會被扭轉.彈性狀態的結構抗扭中心被稱作剛度中心，彈塑性狀態的結構抗扭中心被稱作強度中心.當構件處于彈性階段強度中心和剛度中心都是存在的，并且重合，但在彈塑性階段，沒有剛度中心，只有強度中心.并且在彈性階段時，兩個中心是靜止的，在彈塑性階段，強度中心是隨著荷載的作用不斷運動的.如圖1所示.

文章通過對目標模型進行PUSH-OVER分析[1]，得到各層的質量中心、每步抗側力對應的剪力、層間最大位移、節點位移荷載曲線.通過分析數據就能夠得到強度中心、剛度中心與扭轉變形的關系.PUSH-OVER是模擬地震荷載的，所以，力是加在質量上的，因此合力在質量中心上.

2 結構在彈塑性狀態下扭轉

在push-over推覆作用下，取結構層兩端各步位移.

Umax——樓層角點豎向最大層間位移.

Umin——樓層角點豎向最小層間位移.

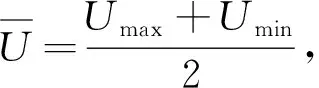
由圖2可知，ξ是角點最大位移與角點最小位移之比的關系.可知，當ξ>1.8，Umax/Umin急劇增大，呈發散狀.

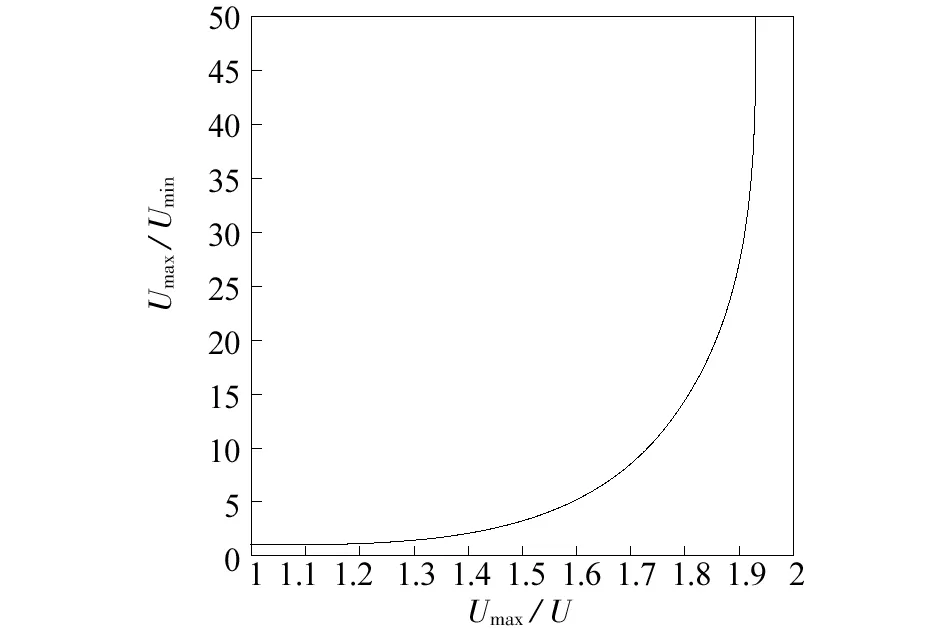
圖2 結構平面扭轉關系圖

3 PUSH-OVER推覆分析步驟

PUSH-OVER是一種靜力彈塑性分析法[2]，按照既定的加載方式對構件施加水平荷載，如果構件開裂就修改構件的剛度，通過不斷的迭代進行下一步運算，逐步將構件推至愈加真實的運動及受力狀態.經過一次又一次的循環，能夠得到構件破壞的全過程，得到每一荷載步構件的基底剪力和頂點位移.

采用完全牛頓-拉夫遜迭代和修正牛頓-拉夫遜并用的方法，在開始時通過修正剛度形成最初的切線剛度，但是在局部的迭代時不再修正.如圖3所示.

圖3 迭代步

推覆加載方式：

(1)確定等效水平推力{P}.

(2)加載{P/5}，求位移{D}.

(3)將{D}作為初始位移，求最大荷載{Pmax}.

(4)取{P/20}作為荷載步長{Δ}.

(5)以步長{Δ}控制進行推覆計算，即荷載步長控制.

(6)若荷載步內3次迭代不能收斂，則下一步采用球面控制法.所謂球面控制法就是在荷載步長控制結果中選擇一個正常迭代結果{Δ}和{D}，令

c=2，定為球面弧長，以后的迭代結果要求滿足弧長控制.

cp和cd為球面半徑.

(7)強度中心的計算

由PUSH-OVER推覆分析可得知每一步各柱或剪力墻所受到的外力FXi，FYi.計算強度中心，需先假定一坐標系.不妨設柱或剪力墻所受到的外力作用于柱或剪力墻的截面形心處，即(Xi，Yi)[3].

強度中心可認為是該結構層各柱或剪力墻所受到的剪力合力作用點[4].計算公式如下：

推覆分析是單側加荷，合力點應該是一條合力作用線.存在扭轉，作用點很不穩定.文章討論的合力點即合力作用線.

4 計算模型

4.1 工程概況

該工程是辦公樓，長26.6 m，寬29.3 m，高17.8 m，框架為不規則結構.底層高5.1 m、第二、三層高3.9 m、第四層高4.9 m、第五層高4.9 m.抗震設防烈度8度，設計地震分組為第一組，地震加速度值為0.2 g，設計特征周期為0.35 s，場地類別為Ⅱ類，抗震等級一級[5].

根據結構平面布置的不同，取2種情況.

模型1：三維立體圖如圖4所示，其底層結構平面圖(左下角柱點為原點)，如圖5所示.

圖4 模型1三維立體圖

圖5 模型1底層結構平面圖

模型2：在第一種情況的基礎上，在1～4層圖示位置增設一道剪力墻，三維立體圖如圖6所示，其底層結構平面圖如圖7所示.

圖6 模型1三維立體圖

圖7 模型2底層結構平面圖

結構材料均采用C30混凝土.

4.2 靜力推覆分析

第一種情況:底層質量形心坐標(14.89 m，11.95 m)，剛度形心坐標(15.56 m，12.00 m).

0度靜力推覆分析加載了84步，可得在0度推覆水平時位移荷載曲線，及各載荷步的柱剪力分析表，如圖8，表1所示.由圖可知，當荷載步在1到71步之間時，結構發生塑性變形，71到84步之間，塑性變形十分明顯.

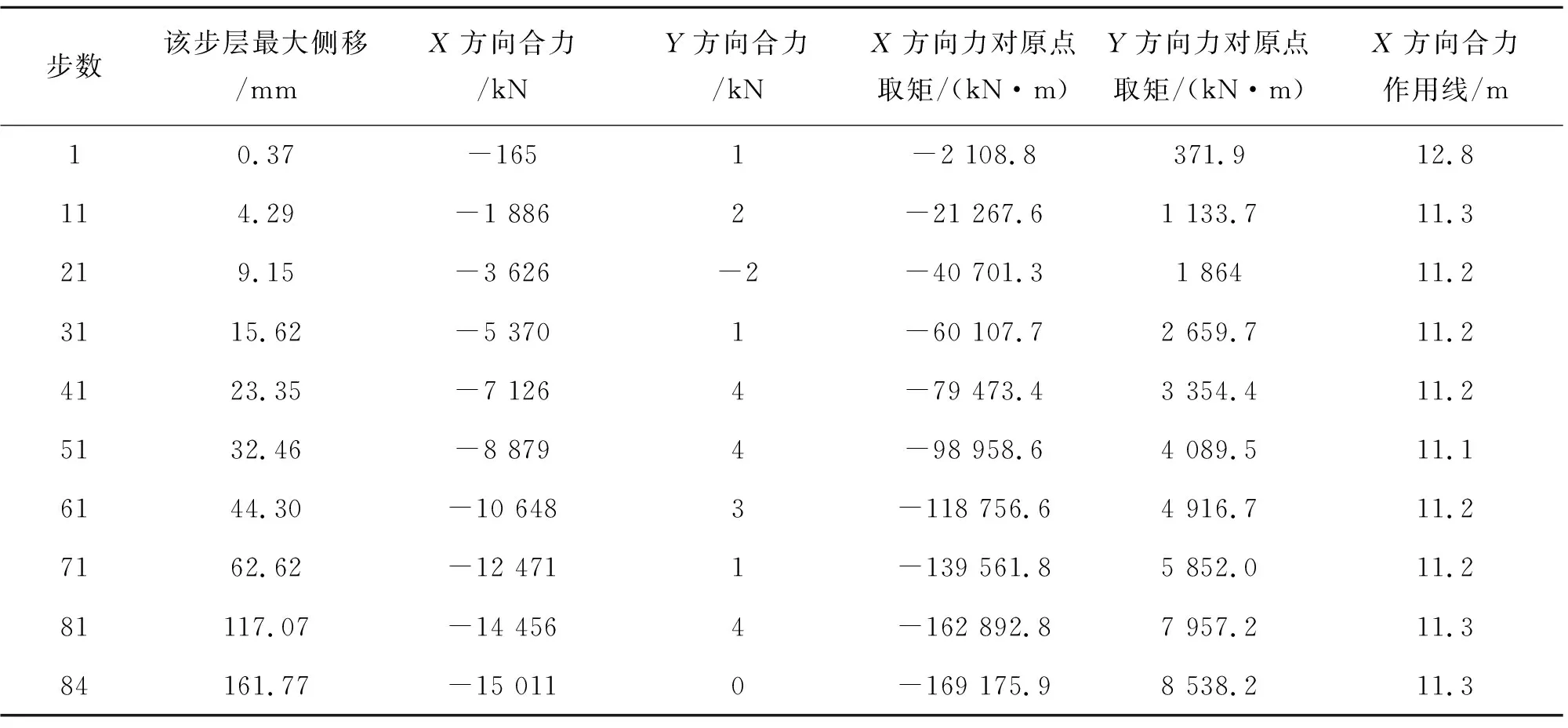
表1 一層柱剪力分析

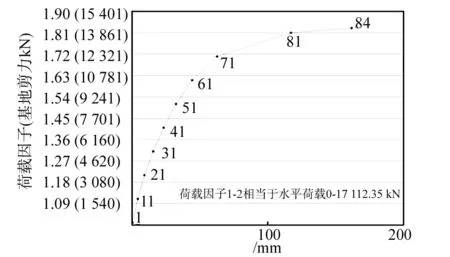
圖8 模型10度推覆底層水平位移荷載曲線

第二種情況:底層質量中心坐標(14.596 m，11.722 m)，剛度中心坐標(10.024 m，4.158 m).

0度靜力推覆分析加載了100步，可得在0度推覆水平時位移荷載曲線，及各載荷步的柱剪力分析表，如圖9，表2所示.由圖9可知，在受力范圍內結構產生得塑性變形并不明顯.

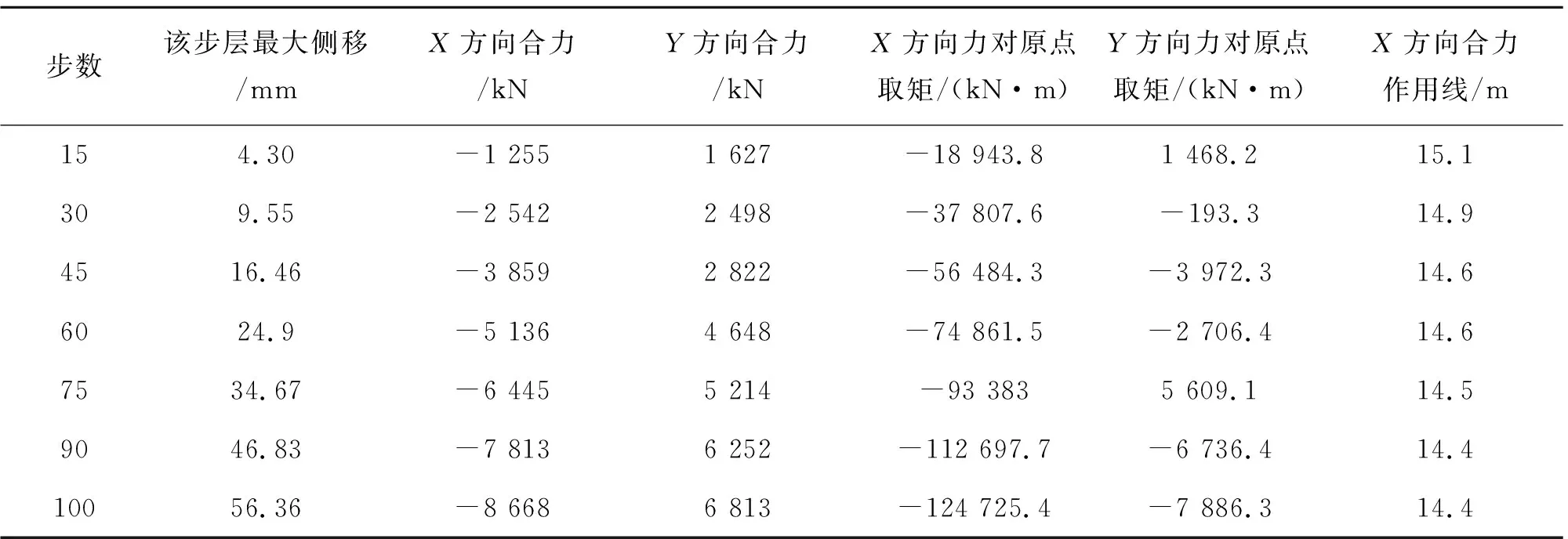
表2 一層柱剪力分析

圖9 模型20度推覆底層水平位移荷載曲線

4.3 數據分析

將底層結構的強度中心看做初始位置，以各步層最大水平位移為橫坐標，強度中心偏移為縱坐標繪制圖10.

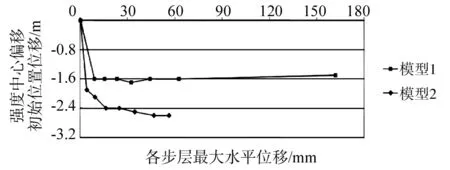
圖10 強度中心偏移過程

模型1框架結構不規則，但是剛度對稱性較好，由圖10可知,最終強度中心偏移1.6 m，之后結構破壞.模型2框架結構不規則，剛度對稱性亦較差，隨著塑性發展，最終強度中心偏移2.6 m.

結構在彈塑性狀態下扭轉情況如表3和表4所示，可知模型2的扭轉變形ξ大于模型1.

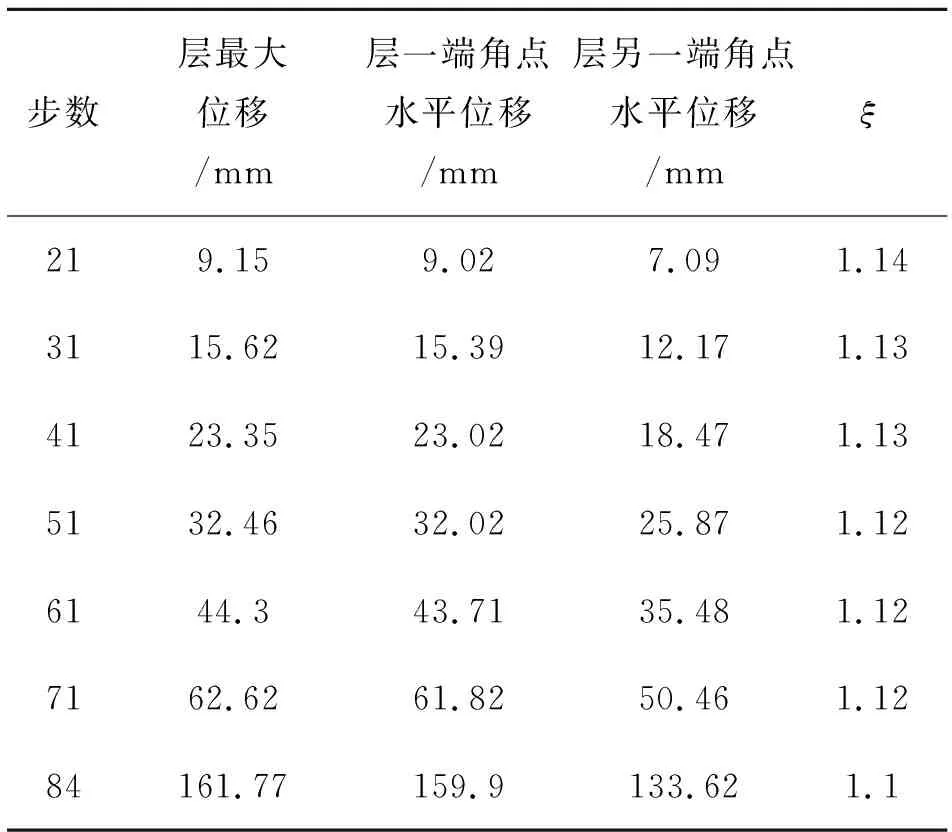
表3 模型1扭轉情況

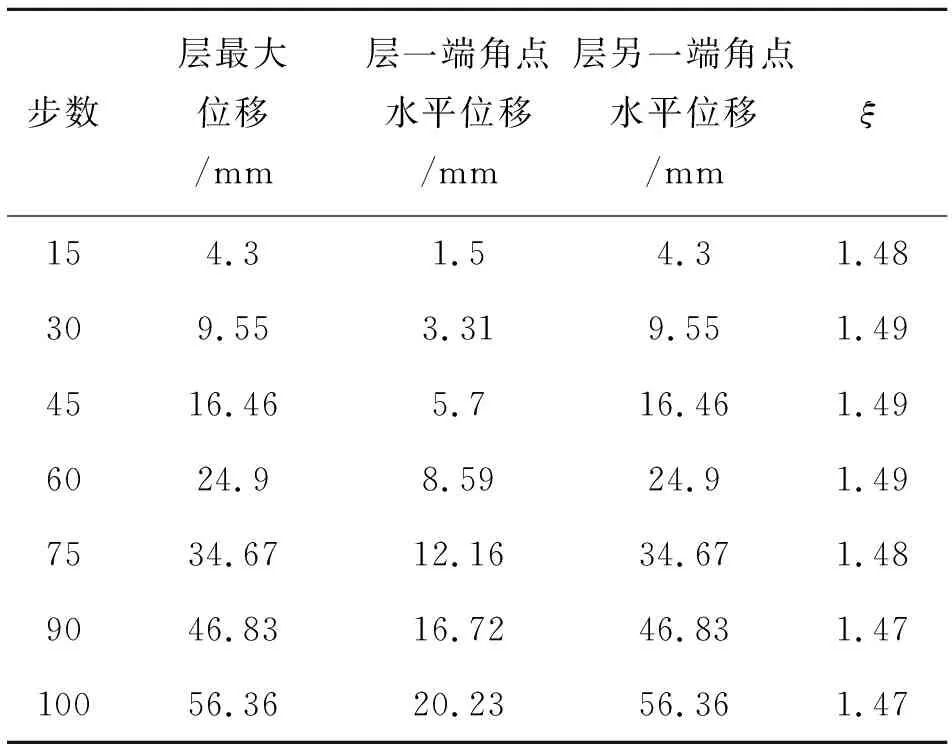
表4 模型2扭轉情況

5 結論

根據強度中心和剛度中心的移動，所得結論如下：

(1)結構幾何形狀規則，同樣的結構，在質量分布不同的情況下，抗震性能不一樣.設計中通常采用的控制剛度中心的做法無法規避扭轉破壞，應該重視強度中心的移動過程對結構產生的影響.

(2)剛度和幾何都不對稱的混凝土結構，隨著靜力推覆，強度中心有逐步向質量中心靠近的趨勢，扭轉變形逐步減小，與彈塑性狀態下非對稱結構的扭轉變形相對應.