基于多尺度卷積神經網絡的高光譜圖像分類

劉 娜，宋 娟，董 麗，尤洪峰

(1. 青島黃海學院智能制造學院，山東青島 266427；2. 新疆大學 信息科學與工程學院，新疆烏魯木齊 830000)

1 引言

高光譜圖像(HSIs)在每個像素中包含數百個波段。由于高光譜圖像光譜的豐富性，它們被廣泛用于農業[1]、林業[2]和城市分區等[3]。豐富的波段給HSIs圖像帶來了足夠的特征的同時也產生了許多冗余特征。最近，研究人員提出了一些新的方法來解決冗余特征。聶飛平[9]等提出了一種特征自動加權模型，使得冗余特征最小化。Ayinde等人[10]通過為不同的冗余特征建立相對余弦距離，最終消除了大量冗余特征并降低了模型計算成本。主成分分析(PCA)在消除冗余特征方面起著重要作用[11-14]，并且它不受參數設置的影響，所以選擇了PCA模型做特征預處理。小樣本HSIs也是特征挖掘和分類中的一個難題。為了更好地實現高光譜圖像的小樣本分類，研究者們做了大量的研究，如支持向量機(SVM)[4]，條件隨機場(CRF)[5]，k最近鄰(KNN)[15]，基于聚類[16]等。然而，上述方法對挖掘高維特征不夠充分。近年來，深度學習由于其強大的特征學習和分類能力，在圖像分類方面取得了越來越大的成就[17]。為了更好地挖掘高維特征，Mesut Salman[6]等人使用AlexNet提取高光譜圖像的形態特征，并通過形態特征來加強特征間的空間關系；Mercedes E.Paoletti等人[7]提出了一種殘差神經網絡(ResNet)，逐步增加卷積維數，最終實現冗余特征的消除。Gefei Yang 等人[8]提出了一種雙通道稠密卷積網絡(DenseNet)來提取高光譜圖像的光譜特征和空間特征，并通過充分利用多種特征進一步提高了圖像分類的精度。以上方法在特征挖掘中表現出優異的性能。

然而，由于卷積核的大小決定了最終學習的特征，且高光譜圖像具有高維特征的性質，使得單個卷積核難以適用。雖然深層網絡可以通過挖掘更深的特征來獲取更多的信息，但隨著模型層數量的增加，大量的有用特征同樣被丟失。最終導致復雜的小樣本高光譜圖像識別變得困難。H Lee[18]等人提出了上下文CNN挖掘不同尺度的高光譜圖像特征，并取得了良好的效果，但這方面的工作只是對輸入部分進行了改進，模型的中后期對特征的挖掘還不夠全面。為了解決上述問題，提出了一種MSC運算方法，在整個網絡中同時對每個模塊提取不同尺度的卷積特征。實驗結果表明，該算法能較好地挖掘高光譜圖像的特征。這篇文章的主要貢獻如下：1)首次將MSC方法應用于任意模型中的每個卷積模塊。這種方法特別適用于樣本有限的小規模數據集。2)為了更好地理解MSC卷積的訓練結果，對三個公共數據集進行了收斂性可視化分析。

2 模型結構

圖1顯示了基于AlexNet算法提出的MSC運算方法。首先，利用PCA算法對原始高光譜圖像進行降維，保留其大部分信息維數，降低了計算量。其次，將降維后的特征輸入改進后的AlexNet模型，最后通過Softmax預測每個像素并實現識別。

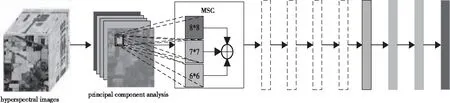
圖1 改進后的AlexNet模型

圖1中，MSC代表提議的MSC，虛線表示MSC方法，綠色矩陣表示Maxpooling層，藍色矩陣表示密集層，紫色矩陣表示Softmax函數，⊕表示特征融合操作。

2.1 傳統卷積

卷積可以根據給定的權重自動計算特征，最終保留有用的信息(如圖像方向邊、線、點等)。局部信息通過Flatten 層組合得到圖像的全局信息。每個卷積核對應于一個基本特征，并且生成一對特征映射，并且共享特征圖中的權重。傳統的卷積運算如圖2所示。

圖2 傳統的卷積運算過程

圖2 中，綠色矩陣表示輸入特征，橙色矩陣表示3的卷積核，粉紅色矩陣表示輸出。

傳統的卷積公式如下所示

i，j代表了圖像輸入特征點的橫坐標和縱坐標；n代表了卷積運算的次數；X代表了圖像特征矩陣；Wk代表了卷積核為k的權重矩陣；bk代表了卷積核為k的偏置函數；S表示得到的新特征矩陣；*表示卷積運算公式。

2.2 多尺度卷積

特征挖掘直接受卷積核尺度的影響。有時單個卷積核不能充分挖掘復雜圖像中的關鍵特征，導致一些關鍵特征的丟失。為了解決上述問題，提出了一種新的MSC方法，通過多個卷積核利用多個尺度同時挖掘特征。實驗結果表明，MSC能更多的保留關鍵特征。MSC運算如圖3所示。

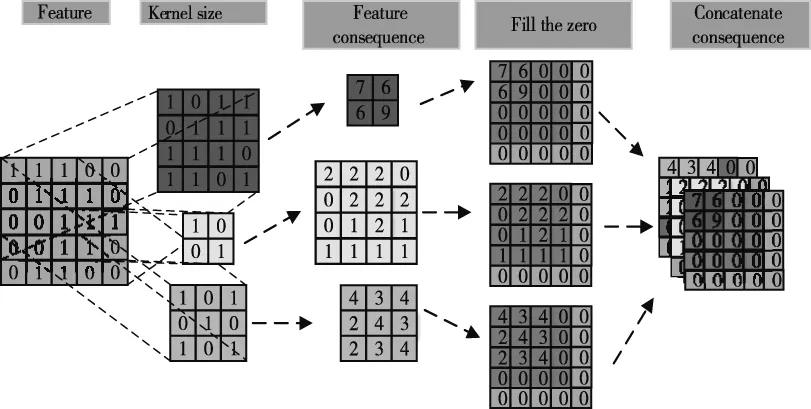
圖3 MSC運算過程

圖3中，綠色表示輸入特征；紅色、橙色和黃色表示不同尺度下卷積核的大小，粉色表示各卷積核運算結果；多顏色矩陣表示輸出的特征結果；多尺度特征通過級聯融合作為下一模塊的輸入。

多尺度卷積公式如下所示：

W(k-1，k，k+2)代表了k-1，k，k+1 三個不同尺度的卷積核運算；b(k-1，k，k+1)分別代表了k-1，k，k+1 三個卷積的偏執函數。

2.3 特征融合與分類

首先提取包含豐富空間信息和光譜信息的三維特征矩陣D(x，y，b)，然后利用PCA算法進行降維，保留其包含重要特征的維數。最后，將降維的3-D特征矩陣轉換為2-D(x*b，y)特征矩陣作為模型輸入。公式如下：

Input=Reshape(PCA(Dx，y，b))

PCA代表了降維算法；Reshape代表了維度轉換函數；Dx，y，b代表了原始特征數據；Input代表了模型輸入矩陣；x表示圖像的橫向長度；y代表了圖像的縱向長度；b表示圖像的光譜緯度。

當特征被輸入到MSC運算方法時，每個卷積核分別計算其特征，最后將生成的多尺度特征融合，其公式表示如下：

溫度是影響生物生命活動的最重要的環境因子之一。一般能在45℃以上生長和繁殖的細菌可稱為高溫菌，主要包括部分細菌，古菌和真菌［10］。ClpP存在于細菌和真核生物中，除了柔膜細菌和部分真菌外［11］。它是高度保守的絲氨酸蛋白酶。ClpP最早發現于大腸桿菌中［12］。ClpP的結構有一個共同點:它包含了14個亞單元，有兩個七瓣環形成一個圓柱樣結構，該結構圍成一個大腔室內含蛋白酶的活性部位［13］。ClpP能形成AAA+(ATP酶聯合不同細胞間的活性)伴侶蛋白復合物，它可以使底物變性以及通過軸孔把它們轉移到蛋白酶的蛋白水解腔室中進行降解，將蛋白降解成7～8個殘基后從腔室中釋放出來［14］。

Output=Concatenate(F1⊕F2⊕F3)

Output代表了最終多尺度特征融合后的輸出; Concatenate特征融合函數；F1代表了卷積核尺寸為 k-1的運算結果；F2代表了卷積核尺寸為 k的運算結果；F3代表了卷積核尺寸為 k+1的運算結果；⊕代表了融合運算公式。

3 數據集及實驗結果

3.1 數據集及評估方法

在這篇文章中，實驗是基于三個高光譜公共數據集進行的。第一個數據集是Indina Pines，其大小為145*145，并通過PCA降至到100維，整個圖像有16個不同的類。第二個數據集是Pavia University，其大小為610*340，并通過PCA降至到50維。整個圖像有9個不同的類。第三個數據集是Salinas，其大小為512*217，并通過PCA降至到29維。整個圖像有16個不同的類。總體準確度(OA)、平均準確度(AA)和kappa coefficient (Kappa)被用作評估所提算法策略的性能指標。

表1 部分MSC模塊的算法模型

3.2 傳統卷積與MSC卷積性能比較

為了比較單卷積與MSC性能哪個更好，在三個數據集上驗證了它。構造了一組卷積核尺度由3，4，5組成的MSC和單卷積3，4，5比較。實驗一共運行了100輪，每輪迭代20次。實驗結果如圖4所示。從圖4可以看出，本文提出的MSC在特征挖掘和收斂方面都有更好的表現。

圖4 收斂曲線(紅色線代表了MSC運算。其它顏色線代表了單卷積運算)

3.3 不同模型在不同數據集上的實驗結果

為了進行公平的比較，在本實驗中，將MSC運算到三個經典的深度學習分割算法中，包括AlexNet[6]，ResNet[7]，DenseNet[8]，并與原算法進行比較。不同數據集的結果顯示在下表中(其中表2為Indian數據集；表3為Pavia大學數據集和表4為Salinas數據集)。

表2 提取5%，10%，15%的Indian數據集的樣本作為訓練集實現分類，其中粗體表示改進算法之后的結果

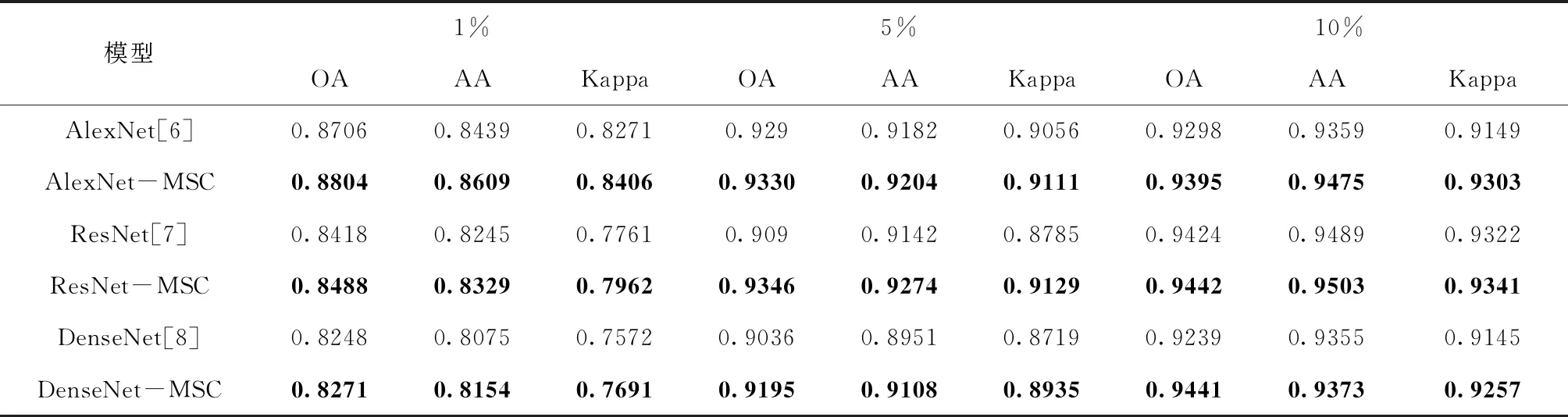
表3 提取1%，5%，10%的Pavia數據集的樣本作為訓練集實現分類，其中粗體表示改進算法之后的結果

表4 提取1%，5%，10%的Salinas數據集的樣本作為訓練集實現分類，其中粗體表示改進算法之后的結果

1) Indian數據集的結果：印度松樹數據集屬于小樣本數據集，其中9個類小于500個樣本，最小類只有20個樣本。從表2中，可以清楚地看到，提出的MSC運算效果比單卷積的效果高2%到4%，對OA、AA和Kappa都是如此。圖5對實驗結果進行了可視化(使用5%的樣本作為訓練集進行訓練)。可以清楚地看到，改進后的模型顯著提高了分類精度(通過紅色圓圈展示了原始算法與改進算法在某些地方的明顯差異)。

圖5 Indian數據集可視化結果

2) Pavia數據集的結果：該數據集分為9類，每類有數千個樣本，但樣本形狀不規則。從表3可以清楚地看出，改進的卷積算法提高了OA，AA和Kappa，并且評估標準隨著訓練樣本數量的增加而顯著增加。圖6對實驗結果進行了可視化(使用1%的樣本作為訓練集進行訓練)。可以清楚地看到，隨著訓練樣本比例的增加，噪聲顯著降低。相對于傳統的單卷積算法，改進的卷積算法的分類效果明顯更強。

圖6 Pavia數據集可視化結果

圖7 Salinas數據集可視化結果

4 總結

針對傳統卷積挖掘深層特征會導致部分關鍵特征丟失，從而給小樣本分類帶來困難的問題。本文提出了一種MSC卷積運算算法改進了傳統卷積運算方式，通過同時計算多個卷積并融合運算后的多尺度深層特征，有效地保留了更多關鍵性特征。在三個公共數據集和三個改進算法上取得了最好的結果。充分證明了本文方法的可行性。下一步將研究關鍵特征間的序列問題，從而通過增強特征間的關系來獲取更高的分類效果。