虛擬軌道列車循跡控制優(yōu)化模型與仿真研究

曾厚銘，車 超，解 靜，賈尚帥

(1. 西南交通大學(xué)牽引動力國家重點實驗室，四川 成都 610031；2. 中車長春軌道客車股份有限公司基礎(chǔ)研發(fā)部，吉林 長春 130062；3. 中國人民解放軍96901部隊24分隊，北京 100094；4. 中車唐山機車車輛有限公司技術(shù)研究中心，河北 唐山 064000)

1 引言

伴隨城市化進程的加快，公共交通運輸越來越難以滿足人們?nèi)找嬖鲩L的出行需求。雖然興建地鐵、輕軌、空軌等可以有效緩解公共交通壓力，但是其建設(shè)周期長、成本高。另一方面，國家新近出臺的國辦發(fā)[2018]52號文件進一步規(guī)范了城市軌道交通修建，大多城市尚不滿足相關(guān)修建要求。在這種情況下，研發(fā)具備較高運載能力，可以在既有道路上行駛的新型城市軌道交通運輸方式勢在必行。虛擬軌道列車[1，2]就是一種符合這些特點和要求的新型城市交通運輸方式。

虛擬軌道列車是智能軌道快運系統(tǒng)的運載工具[3]，是通過膠輪承載、以地面虛擬軌道為導(dǎo)向運行的道路列車，其軌道非傳統(tǒng)鋼軌而是在道路上鋪設(shè)感應(yīng)標識形成的虛擬軌道，是一種地面自導(dǎo)向新型城市軌道交通工具。虛擬軌道列車的循跡控制是通過車載感知系統(tǒng)獲取車體與虛擬軌道之間的相對位置和姿態(tài)，結(jié)合車體運動狀態(tài)和周邊運行環(huán)境等因素生成控制決策，旨在實現(xiàn)循跡行駛和協(xié)同轉(zhuǎn)向，是虛擬軌道列車的一項關(guān)鍵技術(shù)。德國弗勞恩霍夫交通和基礎(chǔ)設(shè)施系統(tǒng)研究所針對實現(xiàn)循跡行駛和最小化橫向鉸接力這兩個目標，提出了一種三節(jié)編組車輛除首車外所有后車(以下簡稱后車)的橫向控制模型[4，5]。車輛在該模型的控制下，穩(wěn)態(tài)時能實現(xiàn)良好的循跡效果，但在進出圓形軌道時的循跡偏差較大，且越靠后的車輛調(diào)整時間和超調(diào)量都越大，說明該模型對于軌道曲率變化時的循跡效果不佳。因此本文在其基礎(chǔ)上提出一種優(yōu)化模型，對原模型在軌道曲率變化時的循跡效果進行改善；基于虛擬樣機分析軟件ADAMS(Automatic Dynamic Analysis of Mechanical Systems)及其二次開發(fā)技術(shù)建立三節(jié)編組的虛擬樣機模型并實現(xiàn)循跡控制仿真，驗證所提出的優(yōu)化模型的控制效果。

2 循跡控制優(yōu)化模型

原模型在軌道曲率變化處，如由直線進入圓形軌道，當首車開始入彎時，后車還處在直線軌道上，但此時后車后軸已開始轉(zhuǎn)向，雖然使用一階慣性環(huán)節(jié)進行遲滯，但循跡效果不佳，究其原因是一階慣性環(huán)節(jié)的響應(yīng)與理想轉(zhuǎn)角變化不符。因此在原模型的基礎(chǔ)上，將原模型的一階慣性環(huán)節(jié)改為增設(shè)多個傳遞環(huán)節(jié)，使其響應(yīng)盡可能逼近理想轉(zhuǎn)角。

2.1 后車后軸理想轉(zhuǎn)角計算

當跟蹤點設(shè)置在鉸接處時，嚴格循跡的狀態(tài)下各后車的運動狀態(tài)都完全相同，后軸的理想轉(zhuǎn)角變化也相同，循跡控制容易實現(xiàn)。因此，循跡優(yōu)化模型的跟蹤點設(shè)置在鉸接處。

以第i節(jié)車為例，將其簡化為如圖1所示的幾何模型，車輛尺寸參數(shù)L，lF，lR，l均為已知，目標軌道半徑R可由首車運動狀態(tài)計算得到。從第i節(jié)車前鉸Gi-1抵達直線與圓的交界處時，認為其開始入彎，圖1中的粗虛線就表示該時刻的車輛狀態(tài)。根據(jù)跟蹤點在目標軌道上運動且速度方向與目標軌道相切的性質(zhì)，得到該車速度瞬心Mi，再根據(jù)幾何關(guān)系，求解后軸A2i的理想轉(zhuǎn)角。

圖1 后軸理想轉(zhuǎn)角計算原理圖

設(shè)從第i節(jié)車開始入彎后，后鉸Gi移動的距離為s′(0≤s′≤L)，先求Gi與目標軌道圓心O間的距離

(1)

在△Gi-1OGi中，由余弦定理求解ξi-1和βi-1

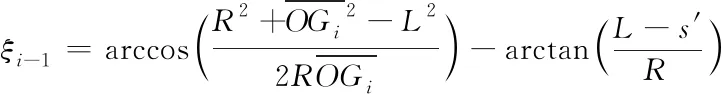
(2)

(3)

從而，求得Mi與Gi-1間距

(4)

在△Gi-1MiA2i中，由余弦定理可得A2i軸的轉(zhuǎn)動半徑

(5)

最后，在該位置時A2i軸的理想轉(zhuǎn)角

(6)

為驗證上述推導(dǎo)結(jié)果，在ADAMS軟件中建立了一個簡化模型，將車輛簡化為桿件，并將跟蹤點使用點線副強制約束在預(yù)設(shè)軌道中線上，給予模型一個初速度，移除重力和摩擦等因素進行仿真，輸出仿真結(jié)果并計算后軸位置處的速度與車體縱軸線間的夾角，所得夾角即為跟蹤點嚴格循跡時的后軸轉(zhuǎn)角。理論推導(dǎo)和簡化模型仿真得到的基于路程的后軸理想轉(zhuǎn)角對比如圖2所示，結(jié)果基本一致。

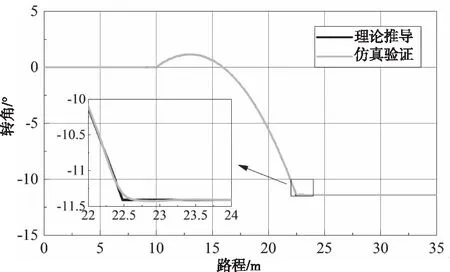
圖2 后軸理想轉(zhuǎn)角理論推導(dǎo)及仿真驗證對比

2.2 后車后軸轉(zhuǎn)角控制模型

將原模型的一階慣性環(huán)節(jié)改為三個由一階、微分、延遲、比例環(huán)節(jié)組成的傳遞環(huán)節(jié)并聯(lián)，其傳遞函數(shù)[6]分別為

(7)

式中，s為復(fù)變數(shù)，X(s)為輸入量的拉氏變換，Y1(s)，Y2(s)，Y3(s)分別為三個傳遞環(huán)節(jié)輸出量的拉氏變換，T1，T2，T3，T4，T5，T6，K1，K2，K3，τ1，τ2為傳遞環(huán)節(jié)的參數(shù)。

以第一個傳遞環(huán)節(jié)為例，進行拉式逆變換，可得微分方程

(8)

式中，x(t)、y1(t)分別表示輸入信號和該傳遞環(huán)節(jié)的響應(yīng)信號。

考慮到實際應(yīng)用，需使用離散形式。同時考慮到車輛的運行速度會發(fā)生變化，后軸轉(zhuǎn)角基于時間遲滯則不能滿足循跡精度的要求，因此將后軸轉(zhuǎn)角基于路程遲滯，將時間常數(shù)T1、T2寫為

(9)

式中，S1、S2為路程常數(shù)，vk表示在第k步時的速度。

此時時間常數(shù)T1、T2變?yōu)榕c當前速度相關(guān)的變參數(shù)，另外用路程延遲S′1代替表示時間延遲的τ1，則式(8)可寫為

(10)

式中，xk、y1k為x(t)、y1(t)的離散形式，分別表示第k步時的輸入信號和該傳遞環(huán)節(jié)的響應(yīng)信號，k1表示第k步的S′1路程前的步數(shù)。

設(shè)第k步時車輛行進的總路程

(11)

式中，Δt為時間步長。

由于Sk是單增的，則k1可由式(12)確定。

Sk1-1≤Sk-S′1≤Sk1

(12)

(13)

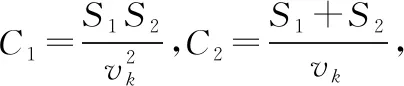
(14)

用同樣的方法可得其余兩個環(huán)節(jié)的響應(yīng)，再將三個響應(yīng)疊加即得最終響應(yīng)。

為使所得響應(yīng)逼近理想轉(zhuǎn)角，需計算參數(shù)X=[S1，S2，S3，S4，S5，S6，K1，K2，K3，S′1，S′2]的最優(yōu)解。該問題的數(shù)學(xué)模型為

s.t.lb≤X≤ub

(15)

式中，nk為總步數(shù)，fk為第k步時的理想轉(zhuǎn)角，ub和lb分別為解空間的上限和下限。

利用MATLAB中的GA函數(shù)，即通過模擬自然進化過程搜索最優(yōu)解的遺傳算法對上述問題進行求解，得到參數(shù)X的最優(yōu)解，從而計算后軸轉(zhuǎn)角基于路程的響應(yīng)，該響應(yīng)與理論推導(dǎo)得出的理想轉(zhuǎn)角對比如圖3所示。

圖3 后軸理想轉(zhuǎn)角與響應(yīng)曲線對比

3 仿真平臺

3.1 虛擬樣機模型

根據(jù)文獻[5]研究的符合虛擬軌道列車特點的雙鉸接道路客車參數(shù)，本文在ADAMS軟件的View模塊中建立了如圖4所示的三節(jié)編組虛擬軌道列車虛擬樣機模型[7]。關(guān)于該模型相關(guān)內(nèi)容的說明見表1。

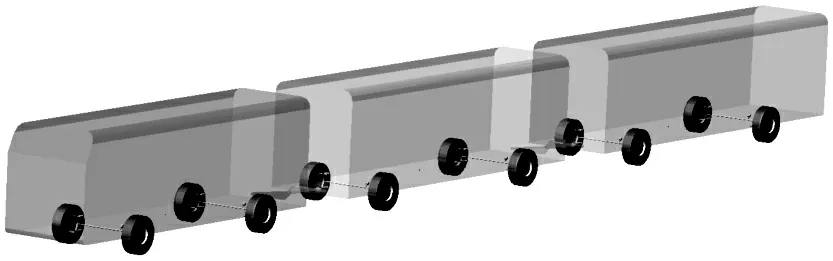
圖4 虛擬軌道列車虛擬樣機模型

表1 虛擬軌道列車虛擬樣機模型說明

3.2 ADAMS二次開發(fā)技術(shù)

ADAMS本身的控制模塊和函數(shù)表達式都不足以實現(xiàn)本文復(fù)雜的循跡控制，因此，需要使用更具有通用性和靈活性的二次開發(fā)技術(shù)。用戶自定義函數(shù)[8]作為一種ADAMS二次開發(fā)技術(shù)的方式，能夠按照用戶的需求，利用通用程序設(shè)計語言(FORTRAN或C)量身設(shè)計ADAMS/View不能提供的函數(shù)并與其連接，這種方法不會折損ADAMS/View的任何功效，對仿真速度也沒有影響。

ADAMS用戶自定義函數(shù)在本文中的應(yīng)用流程如圖5所示。首先使用C語言將運行工況、循跡控制模型、目標軌道都編寫入控制代碼中。隨后使用C++編譯器將控制代碼文件編譯成ADAMS可以直接作為求解庫調(diào)用的動態(tài)鏈接庫(Dynamic Link Library，簡稱DLL)文件，被ADAMS中每個作為執(zhí)行機構(gòu)的Motion調(diào)用。在仿真時，用戶自定義函數(shù)從虛擬樣機模型中獲取需要測量的信息，進而求解出需執(zhí)行機構(gòu)執(zhí)行的命令，在虛擬樣機模型中作動，最終得到列車響應(yīng)。

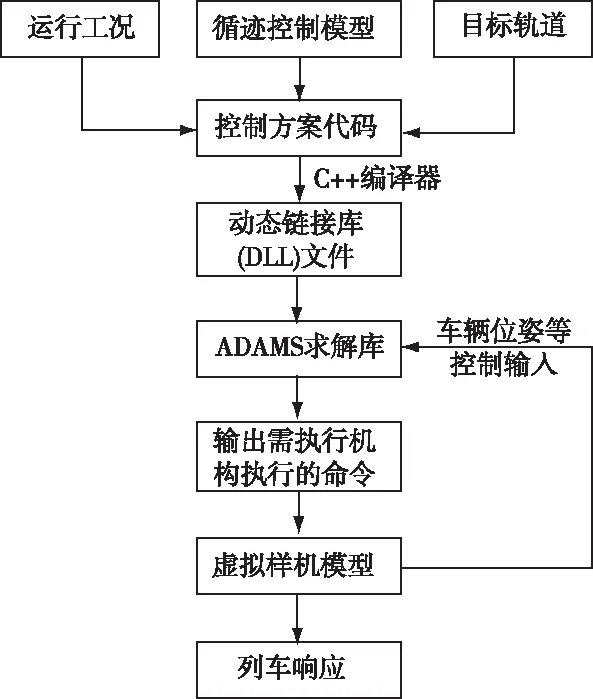
圖5 ADAMS自定義函數(shù)應(yīng)用流程

4 仿真結(jié)果

由于實際道路的道路中線通常由直線和圓弧組成，因此，本文使用的“Ω”形軌道可以模擬列車典型的運行工況。仿真時，列車一開始處在直線軌道上，隨后沿半徑為17.5米的圓形軌道行駛，轉(zhuǎn)過360°后列車再次直行。除了穩(wěn)態(tài)行駛之外，此工況還包括進出圓形軌道的瞬態(tài)，這也是該優(yōu)化模型重點考慮的工況。

該優(yōu)化模型旨在通過控制后車后軸轉(zhuǎn)角在轉(zhuǎn)向行為改變時的變化過程，從而改善循跡效果。仿真結(jié)果中的后車后軸內(nèi)輪轉(zhuǎn)角變化曲線如圖6所示，結(jié)合第2章內(nèi)容可以看出，這一變化過程符合本文的預(yù)期。

圖6 后車后軸內(nèi)輪轉(zhuǎn)角

仿真結(jié)果的循跡效果如圖7所示。由于本文將跟蹤點設(shè)置在鉸接處(尾車設(shè)置在車尾處)，而首車單獨進行控制，非本文的研究內(nèi)容，且首車的運動幾乎不受后車的影響，則認為首車循跡效果良好，因此圖7只給出作為參考的預(yù)設(shè)虛擬軌道中線，以及表征后車循跡效果的后鉸和車尾處的運動軌跡和橫向偏差。

圖7 跟蹤點的循跡效果

根據(jù)圖7(a)顯示的結(jié)果，優(yōu)化后跟蹤點運動軌跡與預(yù)設(shè)虛擬軌道中線的重合度高。圖7(b)顯示，列車在穩(wěn)態(tài)時循跡效果依然很好，并且在進出圓形軌道的瞬變過程，該模型也有著顯著的優(yōu)化效果：最大橫向偏差小于0.1m，相較于原模型的小于1.0m降低了一個數(shù)量級。

圖8顯示了前后鉸接的橫向作用力。由于對于后車前軸的轉(zhuǎn)角控制仍然采用德國弗勞恩霍夫?qū)嶒炇业哪Ｐ汀＜匆韵噜弮绍囋阢q接處的速度方向相等為原則，盡量減小影響循跡行駛的橫向鉸接力。因此本文的結(jié)果與原模型一致，產(chǎn)生的最大橫向鉸接力小于4kN，不會導(dǎo)致輪胎側(cè)向力過大而惡化循跡效果，且鉸接處能承受這種大小的持續(xù)橫向載荷。

圖8 前后鉸接橫向作用力

5 結(jié)語

對德國弗勞恩霍夫交通和基礎(chǔ)設(shè)施系統(tǒng)研究所提出的一種多節(jié)后車橫向循跡控制模型進行了研究，該模型使得車輛在穩(wěn)態(tài)時能實現(xiàn)良好的循跡效果，但在軌道曲率變化時的循跡效果不佳。因此本文在其基礎(chǔ)上提出了一種優(yōu)化模型，將跟蹤點設(shè)置在鉸接處，計算車輛進出圓形軌道的后車后軸理想轉(zhuǎn)角，將原模型的一階慣性環(huán)節(jié)替換為三個組合環(huán)節(jié)，傳遞環(huán)節(jié)參數(shù)通過遺傳算法(MATLAB的GA函數(shù))求得最優(yōu)解。根據(jù)德國弗勞恩霍夫交通和基礎(chǔ)設(shè)施系統(tǒng)研究所研究的符合虛擬軌道列車特點的雙鉸接道路客車參數(shù)，利用ADAMS軟件建立了三節(jié)編組的虛擬軌道列車虛擬樣機模型，并通過ADAMS二次開發(fā)技術(shù)將循跡控制模型應(yīng)用在仿真驗證中。仿真結(jié)果表明，該優(yōu)化模型有明顯的優(yōu)化效果，最大橫向偏差小于0.1m，相較于原模型的小于1.0m降低了一個數(shù)量級。同時，由于仍然對后車前軸采用最小化橫向鉸接力的控制模型，最大橫向鉸接力足夠小，不會對循跡效果產(chǎn)生影響。