增壓速率對多孔金屬篩網泡破壓力影響的實驗研究

馬原, 孫靖陽, 厲彥忠, 汪彬, 李楊

(1.西安交通大學制冷與低溫工程系, 710049, 西安; 2.上海宇航系統工程研究所, 201109, 上海)

針對液體推進劑系統,航天器在軌點火、推進劑在軌傳輸等過程均需要單相液體的穩定供給。微重力條件下,氣液相分布具有很大的隨機性,必須采取推進劑管理技術對貯箱內的氣液相進行控制與管理,才能保障單相液體的穩定獲取[1-2]。篩網式液體獲取裝置(LAD)能夠有效利用表面張力和毛細作用實現液相推進劑的持續獲取,對于流體物性、軌道環境、流量需求等因素的敏感度較低,已經廣泛應用于常溫推進劑的在軌管理,并被認為是低溫推進劑最理想的氣液分離與全液獲取方法[3-4]。

圖1給出了一種四通道篩網式LAD的結構示意圖[5]。貯箱內均勻布置4個液體獲取通道,通道近壁側安裝有一層多孔金屬篩網,其他面為金屬固壁。由金屬細絲編制而成的篩網具有大量微米級孔隙,能夠依靠表面張力和毛細作用引流液體進入通道匯集于出液口,同時對氣體發揮阻隔作用,從而實現氣液分離與單相液體的獲取。

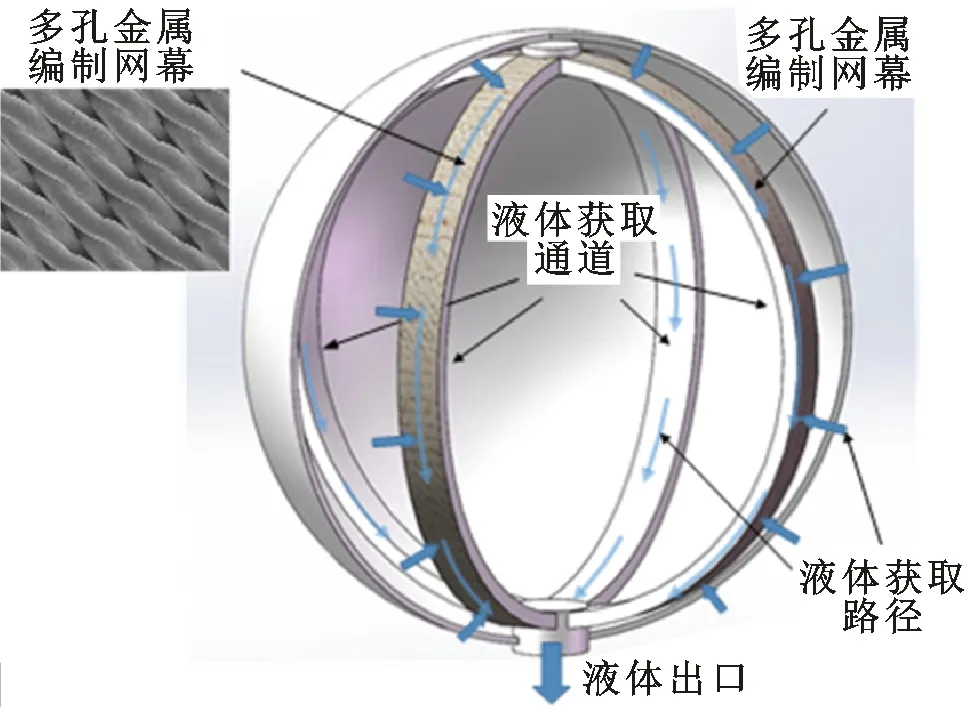
圖1 篩網通道式LAD液體獲取過程示意圖[5]Fig.1 Schematic diagram of the liquid acquisition process of the screen channel LAD[5]

該裝置的氣體阻隔作用主要反映為金屬篩網的泡破壓力,泡破壓力越大,氣體阻隔能力越強[6]。早期,研究學者針對甲醇、水、硅油、氟利昂等多種常溫流體開展了金屬篩網泡破壓力的實驗研究[7-9]。隨后,NASA研究人員先后對金屬篩網在液氧、液態甲烷、液氮、液氫等低溫流體內的泡破壓力進行了實驗研究,考察了篩網類型、流體溫度、系統壓力等因素對篩網泡破性能的影響規律[10-12]。然而,相關文獻雖然提供了大量的泡破壓力測量數據,但是并未針對泡破測量過程的特性規律以及實驗數據處理方法給出詳細介紹。

我國在低溫推進劑氣液管理方面的研究起步較晚,針對篩網式液體獲取裝置,Ma等對荷蘭斜紋篩網(DTW)的液體芯吸特性開展了常溫及低溫實驗測試,并構建了反映低溫流體蒸發作用的芯吸計算模型[13-17]。針對篩網的泡破壓力特性,國內尚未開展系統的深入研究。因此,本文針對3種編織密度的DTW篩網,采用異丙醇為實驗工質,開展了不同增壓速率下的泡破壓力可視化測試,并基于靜態泡破壓力模型計算得到了3種篩網樣本的有效微孔直徑。相關工作可為LAD性能評估、設計優化以及空間低溫系統方案設計提供理論依據和技術參考。

1 泡破壓力預測模型

泡破壓力ΔpBP是指第一個氣泡穿透時篩網兩側的壓差。圖2給出了金屬篩網內任一微孔的剖面示意。首先,液體(僅適用于與壁面接觸角小于90°的潤濕性液體)在毛細力驅動下能夠完全填充孔隙并在孔隙中通流。在表面張力的作用下,氣液界面兩側能夠承受一定的壓差,封阻氣相的穿過。當氣相側壓力不斷升高使篩網兩側壓差超過泡破壓力時,孔隙內氣液界面將無法繼續阻止氣體穿過,從而失去全液獲取能力[9]。

圖2 氣相穿透潤濕篩網微尺度通道的過程示意圖Fig.2 Schematic diagram of the bubble breakthrough across the micro-channel in the wet screen

基于毛細理論,兩靜態流體界面間因表面張力引起的壓力差可以通過楊氏-拉普拉斯方程進行計算,合力方向指向界面凹面所指方向[18]。該壓差與流體表面張力、界面曲率等因素有關,如下式所示

(1)

式中:p(+)、p(-)為界面凸側、凹側界面壓力;σ為表面張力;Rmax、Rmin為界面最大、最小曲率半徑。對于橫截面為圓形的直毛細管(見圖3),Rmax與Rmin相等,上式可以簡化為[19]

(2)

式中:θ為接觸角;dc為毛細管直徑。

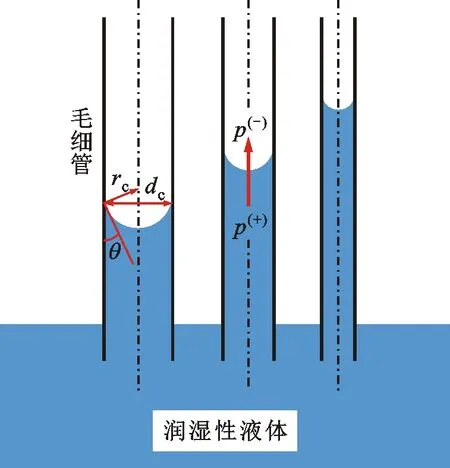
圖3 潤濕性液體毛細現象與界面特征Fig.3 Capillarity action and interface characteristics of wetting liquid

鑒于流體在篩網內的流動與毛細管流動的相似性,研究學者將篩網內部結構復雜的微尺度通道簡化,假設為一組截面為圓形的直通道,且直徑相同的毛細管束,基于式(2)提出了計算篩網靜態泡破壓力的簡化模型[20]

(3)

式中DP為篩網有效微孔直徑,即將篩網內復雜的三維通道結構等效簡化為直通道的、橫截面為圓形的毛細管對應的直徑。DP由篩網編織結構決定,但并不是多孔篩網的客觀結構參數,無法通過直接測量得到,通常采用測量泡破壓力的方法由式(3)反算獲得[21]。由于不銹鋼材料熱膨脹系數較小,應用于不同溫區時不會產生明顯的結構變化,即篩網DP基本不變[22]。經實驗數據驗證,式(3)能夠廣泛適用于多種常溫與低溫流體[7-12]。基于此,有研究學者首先采用常溫標準溶液(如異丙醇)進行泡破壓力測試,計算獲得該篩網結構的DP后,替換低溫流體物性對該篩網結構的低溫泡破壓力進行計算預測[23]。

2 泡破壓力測試系統

實驗系統如圖4所示,主要包括液池、增壓腔、壓力調節系統和數據采集系統,增壓腔通過支撐連桿固定于金屬法蘭下端。如圖5所示,篩網樣本通過可拆卸法蘭配合銦絲密封安裝于增壓腔上端面,樣本更換方便。篩網樣本兩側布置有溫度和壓力測點。溫度傳感器采用Lakeshore鉑電阻PT111,精度0.1 K。壓差傳感器采用EJA110E,精度0.055%。

圖4 可視化泡破壓力測試系統簡圖 Fig.4 Diagram of the visual testing system for bubble point pressure

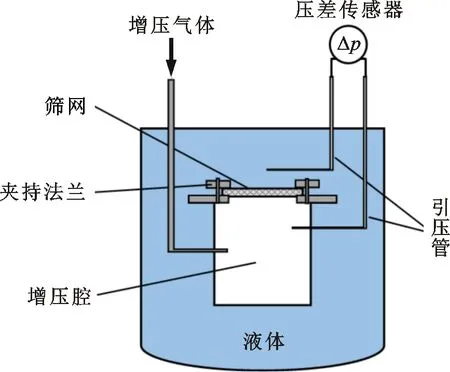
圖5 篩網樣本安裝位置Fig.5 Installation site of the screen sample

開展實驗時,首先加注液體至液位完全沒過增壓腔,待系統穩定后打開調節針閥向增壓腔注入氣體,建立增壓腔內外壓差,即篩網樣本兩側壓差。增壓速率通過調節針閥開度進行控制。篩網樣本上、下兩側壓力分別由引壓管引入壓差傳感器進行測量。增壓過程中,當觀測到有氣泡冒出時表示篩網樣本發生泡破,測量得到的篩網兩側壓差數據即為泡破壓力。

本次實驗采用3種編織密度的DTW不銹鋼篩網作為測試樣本,具體參數列于表1。以DTW 200×600為例,表示一平方英寸(6.451 6 cm2)的篩網由200根經絲和600根緯絲編織而成。由于經緯絲直徑和數量的差異,所形成的篩網有效微孔直徑不同,導致不同篩網針對相同流體的泡破壓力不同,如式(3)所示。實驗工質采用異丙醇,相關物性參數列于表2。

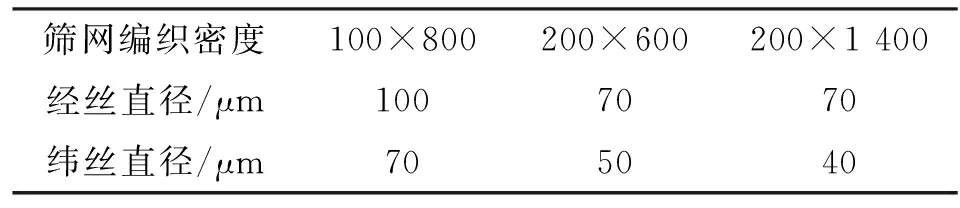
表1 DTW篩網樣本結構參數

表2 異丙醇物性參數[23-24]

3 結果與討論

本文針對3種篩網樣本在異丙醇中的泡破特性開展了多組變工況測試。

圖6 泡破壓力測試過程的典型數據曲線Fig.6 Typical data curve of the testing process of bubble point pressure

圖6展示了一組DTW 200×600測量過程的壓差數據。開始測試前,篩網兩側壓差很小。在25 s左右打開進氣閥,增壓腔壓力伴隨氣體注入不斷上升,注氣速率較為穩定,篩網兩側壓差基本呈線性增長。圖6所示工況的增壓速率約為20 Pa·s-1,在100 s左右壓差達到最大值,同時觀察到篩網上有氣泡溢出,這個壓差峰值即為該工況下的泡破壓力。伴隨著泡破過程對增壓腔的泄壓作用,篩網兩側壓差產生了一定程度的回落。隨后,注氣的增壓作用與泡破的泄壓作用逐漸達到動態平衡,篩網兩側壓差在一定范圍內穩定波動。

針對3種篩網樣本,分別開展了多組不同增壓速率下的泡破壓力測試。以DTW 100×800篩網樣本為例,取4組典型工況進行對比分析,結果如圖7所示,可見增壓速率較小的兩組工況曲線呈現出與圖6相似的變化規律。

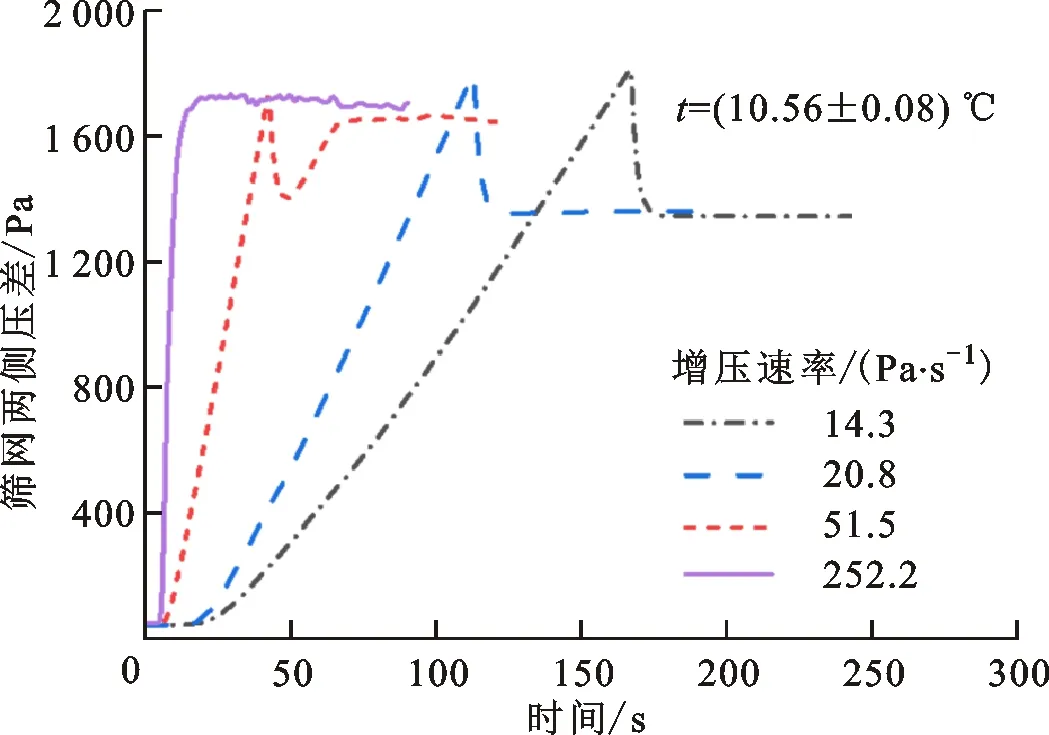
圖7 不同增壓速率下篩網壓差數據曲線Fig.7 Curves of the pressure difference across screen at different pressurization rates

進一步提高增壓速率,壓差曲線雖然仍具有線性增壓和達到峰值后回落的變化特點,但最終達到動態穩定的壓差明顯高于低增壓速率工況的穩定值(51.5 Pa·s-1工況曲線)。這主要是由于流量越大,篩網流動阻力越大引起的。當增壓速率繼續增大至一定值后,篩網壓差轉變為迅速升高后逐漸趨于穩定波動的變化規律,不再具有明顯的峰值特點(252.2 Pa·s-1工況曲線),最終達到的動態穩定值也更高。

圖8展示了不同增壓速率下DTW 100×800篩網泡破過程的氣泡狀態。當增壓速率較小時,個別位置輕度泡破的泄壓能力即可平衡注氣增壓的作用,動態穩定過程的壓力波動幅度很小。隨著增壓速率的增大,篩網泡破的范圍和強度均隨之增大,從而以更強的泄壓能力抵消不斷提高的增壓作用,其動態平衡過程的不穩定性也就越大。

進一步分析各組數據發現,3種篩網樣本在不同增壓速率下測量得到的泡破壓力呈現出了相似的變化規律,均為先線性降低后趨于穩定,如圖9所示。由圖可知,在增壓速率較小的一定范圍內,提高增壓速率,將導致篩網在更低的壓差下發生泡破,即篩網氣泡阻隔能力下降,當增壓速率增大到一定程度后,將不再對泡破壓力產生明顯的影響。

(a)1.26 Pa·s-1 (b)14.3 Pa·s-1

(c)51.5 Pa·s-1 (d)252.2 Pa·s-1圖8 不同增壓速率下篩網泡破現象Fig.8 Bubble breakthrough across screen at different pressurization rates

由于式(3)為靜態泡破壓力的計算模型,當利用該式求解篩網的有效微孔直徑時,理論上應代入增壓速率為零時測得的泡破壓力。也就是說,理論上,靜態泡破壓力是無法通過實驗測量準確獲得的。因此,本文采用線性擬合方法對不同篩網的靜態泡破壓力進行計算預測。由于泡破壓力隨增壓速率的線性變化關系僅在較低增壓速率范圍內較為明顯,結合不同增壓速率下壓差數據的變化特征(見圖7),僅取具有圖6典型曲線特征的測量數據進行擬合。線性擬合結果已在圖9中注明,線性相關系數R2均大于0.95,反映了良好的線性度關系。

表3列出了3種篩網在異丙醇工質內的靜態泡破壓力,即圖9中線性擬合式的截距。同時,表3還列出了將靜態泡破壓力和流體物性參數代入式(3)計算得到的有效微孔直徑。可以看出,隨著篩網編織密度的增加,篩網有效微孔直徑減小,泡破壓力增大。也就是說,編織越密的篩網具有更強的氣體阻隔能力。

表3 3種篩網樣本的靜態泡破壓力和有效微孔直徑

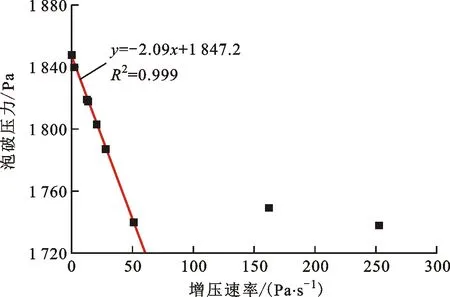
(a)DTW 100×800,t=(10.56±0.08) ℃

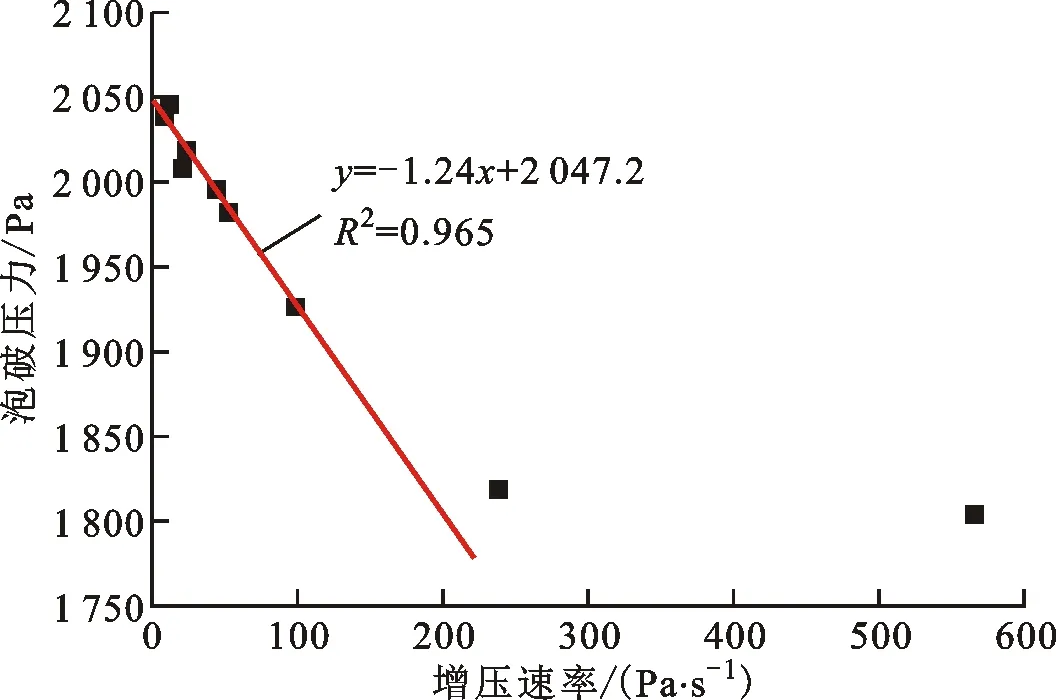
(b)DTW 200×600,t=(10.38±0.15) ℃

(c)DTW 200×1 400,t=(10.64±0.33) ℃圖9 泡破壓力與增壓速率的關系 Fig.9 Relationship between bubble point pressure and pressurization rate

4 結束語

本文針對DTW 100×800、200×600和200×1 400共3種編織密度的不銹鋼篩網,以異丙醇為工質,進行了不同增壓速率下的泡破壓力測試,主要結論如下。

(1)隨著增壓速率的升高,篩網樣本在異丙醇液體中的泡破壓力呈現出先降低后趨于穩定的變化規律,篩網泡破強度不斷增大,從局部小氣泡溢出逐漸轉變為大面積劇烈泡破。

(2)在增壓速率較低時,泡破壓力隨增壓速率呈現出良好的線性遞減趨勢,通過數據線性擬合,得到了3種篩網樣本在異丙醇液體中的靜態泡破壓力,靜態泡破壓力高于動態泡破壓力。

(3)隨著篩網編織密度的增加,篩網有效微孔直徑逐漸降低,泡破壓力逐漸增大,體現出更強的氣體阻隔能力。基于本文獲得的有效微孔直徑,可以通過式(3)對3種篩網在不同流體內的泡破特性進行初步預測。