基于多重廣義Hough變換的多星時頻差聯合定位方法

孫 哲，霍立寰，柏如龍，陳 兵，馬 飛，江 漫

(1.海裝駐邯鄲地區軍事代表室，河北 邯鄲 056000；2.中國電子科技集團第五十四研究所，河北 石家莊 050081；3.河北省電磁頻譜認知與管控重點實驗室，河北 石家莊 050081)

0 引言

無源定位技術無需向待定位目標發射探測信號，利用被動接收的目標輻射的電磁波信號，基于相位差、時頻差等信息對目標進行無源定位[1-2]。近年來，隨著衛星通信技術和相關業務的飛速發展，地面干擾源對衛星通信的威脅也在日益增加。因此，有必要開展衛星平臺的無源定位技術研究。現有的衛星干擾源定位系統以美國的TLS2000系統和英國的satID系統為代表，這些系統采用雙星時頻差定位和三星時差定位等方法，能夠快速、準確地發現廣域范圍內的干擾源目標，在民用和軍事領域都有著重大的應用潛力[3-4]。

基于時差和頻差等信息的定位體制是目前主要的衛星無源定位方法，利用時頻差信息，近年來發展出了多種求解方法[5-14]，大致可以分為迭代類、解析類以及近年來發展的智能算法類。解析類方法包括Chan算法、泰勒級數展開法，這類算法對時頻差測量精度和目標初始值的要求較高。迭代類方法一般以圓球模型近似地球WGS-84橢球模型，利用解析方法計算圓球模型下的定位結果，并逐步迭代逼近真實值。該方法計算簡單，但是算法靈活性較差。智能算法類是近年來發展起來，旨在解決傳統的搜索法計算量大的問題。本質上，多星定位問題實質上是等時/頻差線的交會定位問題。而這種點-線的映射關系，與Hough變換實現的是一種從圖像空間到參數空間的映射關系[15-16]。因此，可以將霍夫變換引入到多站時頻差定位中，靈活地實現多時差/多頻差的單參數定位或多參數聯合定位。然而，傳統的基于Hough變換的定位方法[17-18]僅從原理上進行了驗證，沒有考慮時差和頻差的參數不一致性，實際應用存在困難。

近年來提出的廣義霍夫變換(Generalize Hough Transform，GHT)模型在特征檢測、可視化分析方法中得到了廣泛應用，通過將圖像空間與參數空間靈活映射，代表了從統計角度解決問題的新思路。針對傳統的多星時頻差聯合定位方法推導復雜、計算量大和難以擴展的難題，本文將多星時頻差定位轉化成多個雙星時頻差定位的組合，基于雙星時頻差定位原理構建GHT模型，并且利用每個雙星組合的定位幾何稀釋度(Geometric Dilution of Precision，GDOP)，提出了加權融合的多星時頻差定位模型。相比傳統方法，本文方法實現簡單，并且適用于任意衛星數量、任意衛星構型的時頻差定位，能夠實現更高的定位精度，并且對時頻差測量誤差具有良好的穩健性。

1 多星時頻差定位模型

多星時頻差定位模型可以看作多個主星與輔星構成的雙星定位模型的組合，如圖1所示，首先給出了雙星時頻差定位模型。干擾源目標向主星發射干擾信號，同時信號旁瓣泄露到輔星上。通過時頻差測量方法能夠獲得干擾源在主星信號和輔星信號的到達時間差(Time Difference of Arrival，TDOA)和到達頻率差(Frequency Difference of Arrival，FDOA)。TDOA在地球上對應著一條等時差線，即位于等時差線上的位置的時差相同；同樣，FDOA在地球上對應著一條等頻差線。等時差線和等頻差線交會的位置，即為干擾源目標位置。

圖1 三星干擾源定位示意Fig.1 Configuration of the tri-satellite interference source location

假設干擾源的坐標為(x,y,z)，某個時刻時主星坐標為(x0,y0,z0)，速度坐標為(vx0,vy0,vz0)，第l個輔星的位置坐標為(xl,yl,zl)，速度坐標為(vxl,vyl,vzl)，主星與第l個輔星的時差和頻差分別為τl和fl，滿足：

(1)

式中，c為光速；λ為信號波長；r0，rl分別為干擾源與主星、輔星的距離；v0，vl分別為主星和輔星相對于目標點的徑向速度，即：

(2)

根據地球橢球面模型，目標位置滿足：

x2/N2+y2/N2+z2/[N(1-e2)]2-1=1，

(3)

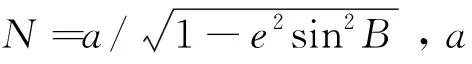
因此，多星時頻差聯合定位方程表示為：

(4)

2 多星廣義Hough變換聯合定位方法

霍夫變換利用了圖像空間和參數空間的映射關系，能夠有效地檢測直線、圓等特征曲線。近年來，霍夫變換在特征檢測、標志識別等領域得到了廣泛應用。而多星時頻差定位本質上是時差/頻差與定位點的映射關系，能夠利用GHT在一定的運算法則下進行表示，從而將多星定位問題轉換為在霍夫空間下的求解問題，相比于傳統的多星定位方法，實現簡單并且易于擴展。

基于GHT，主星與第l個輔星的時差概率密度函數為：

(5)

主星與第l個輔星的頻差概率密度函數為：

(6)

則主星與第l個輔星的時頻差概率密度函數為：

(7)

考慮多星時頻差聯合定位的情況，不同輔星與主星的定位構型不同，所以對不同主輔星組合的時頻差霍夫概率密度函數，需要由不同的加權系數。而GDOP是多星定位領域的一個重要的衡量標準，能夠準確衡量不同定位組合的定位精度。因此，這里采用基于GDOP的加權融合方法，則多星時頻差聯合定位的霍夫概率密度函數表示為：

(8)

式中，wl為主星與第l個輔星的加權系數，即：

(9)

式中，GDOPl,l=1,2,…,L為主星與第l個輔星的雙星時頻差GDOP。

霍夫變換實質上是一種參數空間到圖像空間的網格搜索映射法，霍夫變換精度的提高往往伴隨著大的計算量。針對多星時頻差聯合定位，提出了多重Hough變換策略。首先在廣域范圍內進行粗精度的GHT，然后在搜索到的目標位置附近逐步進行下一重的更高精度的霍夫變換，直至定位結果趨于收斂，從而顯著提升計算速度。

基于多重廣義Hough變換的多星時頻差聯合定位方法步驟如下：

步驟1：初始化參數，經度搜索范圍[Lon1，Lon2]，緯度搜索范圍[Lat1，Lat2]，經度步進steplon，緯度步進steplat，時差測量精度στ，頻差測量精度σf，多重因子μ。

步驟2：計算該重廣義Hough變換函數，在經緯度的網格坐標中，根據式(5)和式(6)分別計算各個主輔星組合的時頻差Hough函數，采用不加權的方式累加后獲得經緯度的初估計。根據式(9)，以該定位結果計算各個雙星時頻差組合的GDOP和加權系數，根據式(8)獲得最終的廣義霍夫函數。對霍夫空間中的累積概率取峰值獲得該重霍夫變換的經緯度估計結果，記為(Lonk,Latk)。

步驟3：計算下一重Hough變換的經緯度搜索步長steplon=steplon/μ，steplat=steplat/μ，經度搜索范圍[Lonk-steplon,Lonk+steplon]和緯度搜索范圍[Latk-steplat,Latk+steplat]。

步驟4：比較經緯度誤差ε=|Lonk-Lonk-1|+|Latk-Latk-1|，若ε<0.000 1，則結束計算，輸出定位結果；若不滿足，則返回步驟2進行下一重的廣義Hough變換。

3 仿真實驗

3.1 算法有效性試驗

首先仿真了理想情況下，多星時頻差Hough變換的結果。主星選擇中星10號，衛星軌位為110.5°E，輔星一選擇中星12號，軌位為87.5°E，輔星二選擇中星6A，軌位為125°E。目標經度為105.65°E，緯度為22.57°E，基于霍夫變換的時頻差變換結果如圖2所示。可以看出，時頻差Hough變換的交點即為目標位置，并且在該時刻下，頻差Hough變換之間的夾角更大，能夠獲得更優的定位精度。

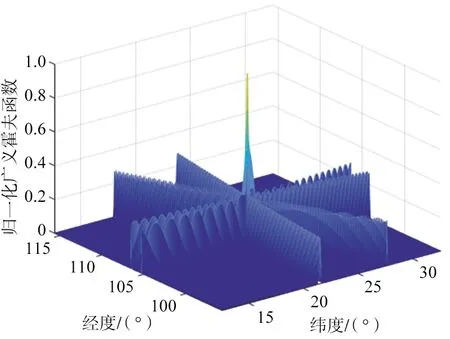
(a) 時頻差Hough變換三維圖

(b) 時頻差Hough變換二維圖圖2 時頻差廣義Hough變換試驗Fig.2 The experiment of the GHT for TDOA/FDOA

定位精度24 h變化情況如圖3所示，以實際的3星定位為例，驗證了算法的有效性。主星選擇中星10號，衛星軌位為110.5°E；輔星1選擇中星12號，軌位為87.5°E；輔星2選擇中星6B，軌位為120.5°E。目標經度為105.65°E，緯度為22.57°E。定位方法選擇3星時差定位、3星頻差定位以及本文所提方法。利用STK仿真某一天的衛星星歷數據，間隔2 h進行定位。其中時差測量的均方根誤差設為1.5 μs，頻差測量的均方根誤差設為10 mHz，蒙特卡洛次數200。可以發現，隨著衛星運動，時差Hough定位和頻差Hough定位的定位精度波動較大，而所提方法都能獲得更高的定位經度。

圖3 定位精度24 h變化情況Fig.3 The varies of the positioning accuracy in 24 hours

3.2 驗證算法穩健性實驗

多時刻定位方法性能影響試驗如圖4所示。以3星組合為例，利用STK仿真0時刻的衛星星歷數據，仿真了不同算法在不同時差測量誤差和頻差測量誤差時定位精度變化情況。圖4(a)仿真了頻差測量的均方根誤差為10 mHz，蒙特卡洛次數為200時，定位精度隨時差測量誤差的變化情況。圖4(b)仿真了時差測量的均方根誤差為1 μs，蒙特卡洛次數為200時，定位精度隨頻差測量誤差的變化情況。通過仿真實驗可以發現，隨著時差測量誤差增加，所提方法的定位精度保持穩定，這是因為在該時刻定位精度受頻差Hough的影響更大，導致聯合Hough定位對時差誤差不敏感；隨著頻差測量誤差增加，所提方法能夠獲得更優的定位精度。

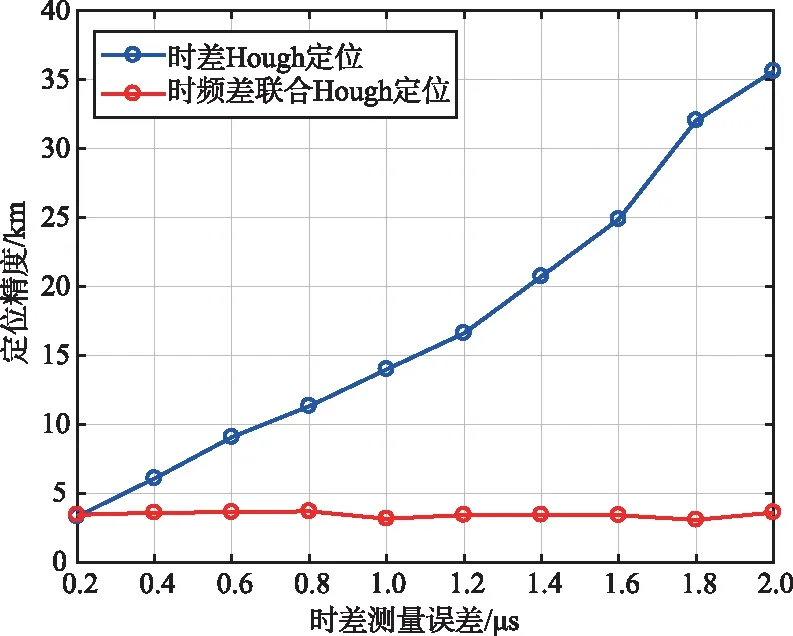
(a) 定位誤差隨時刻個數變化情況

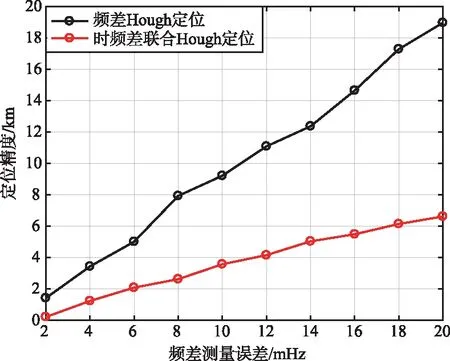
(b) 定位誤差隨時長變化圖4 多時刻定位方法性能影響試驗Fig.4 The experiment of the performance in multi-time positioning method

4 結束語

多星時頻差聯合定位方法具有定位精度高、消除虛假點的優點。然而，傳統的多星時頻差聯合定位方法過程復雜、計算量較大。本文提出了一種基于多重廣義Hough變換的多星時頻差聯合定位方法，將多星時頻差定位模型與廣義Hough變換相互映射。通過多重搜索和GDOP的加權融合，在顯著減小計算量的基礎上，獲得更加穩健的精確定位結果。本文方法實現了廣義Hough變換在多星時頻差定位領域的算法設計、性能分析和仿真驗證，具有良好的工程應用參考價值。