一種緊湊型1024點流水線FFT處理器設計
于 建,霍永華,焦利彬,楊 楊
(1.河北民族師范學院 物理與電子工程學院,河北 承德 067000;2.中國電子科技集團公司第五十四研究所, 河北 石家莊 050081;3.北京郵電大學, 北京 100876)
0 引言
快速傅里葉變換(Fast Fourier Transform,FFT)是基于正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)傳輸方式通信系統中的關鍵性技術,用于傳輸數據在時域與頻域之間的轉化[1]。OFDM作為使用最廣泛的多載波調制技術,已成為多種通信領域的規范基礎[2],如長期演進(Long Term Evolution,LTE)、無線局域網(Wireless Local Area Network,WLAN)以及全球微波互聯接入(Worldwide Interoperability Microwave Access,WiMAX)等[3],同時,OFDM在5G通信系統中仍然是最為主要的調制技術[4]。在OFDM系統中的物理層,FFT處理器是最為復雜的運算模塊,消耗大量的硬件資源[5],因此大量的研究都聚焦于FFT算法與硬件實現架構的優化,達到降低其所消耗的硬件成本。
算法方面,基-2庫里圖基FFT 算法最為著名[6-7],它擁有簡單的蝶形單元,非常適合硬件的實現,但所需的復數乘法運算量大。基-2kFFT算法[8]解決了基-2算法復數乘法運算量過大的問題,同時還能夠保持與基-2算法一樣簡單的蝶形單元,因此非常適合用于FFT處理器的硬件實現。基-2k算法根據k值的不同可分為基-22算法、基-23算法、基-24算法和基-25算法等。
硬件實現架構方面,由于流水線架構(Pipelined Architecture,PA)[9]具有適中的硬件資源消耗與更高的數據吞吐量,常被用于FFT處理器的硬件實現。PA架構又分為前向反饋與負反饋2種風格[10],由于負反饋風格中的SDF架構需要更少的寄存器以及更簡單的控制邏輯,常被用于低硬件成本FFT處理器的設計。
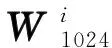
1 算法選擇與評估
考慮到基-2k算法不但擁有與基-2算法一樣簡單的蝶形架構,還能夠減少旋轉因子的運算復雜度,因此本文采用基-2k算法用于1 024點FFT處理器的設計。
不同k值的基-2k算法針對1 024點FFT計算一共包含9個旋轉因子計算階段,只是k值的不同會導致旋轉因子不同。表1所示為不同k值的基-2k算法在計算1 024點FFT時旋轉因子的詳細分布情況。
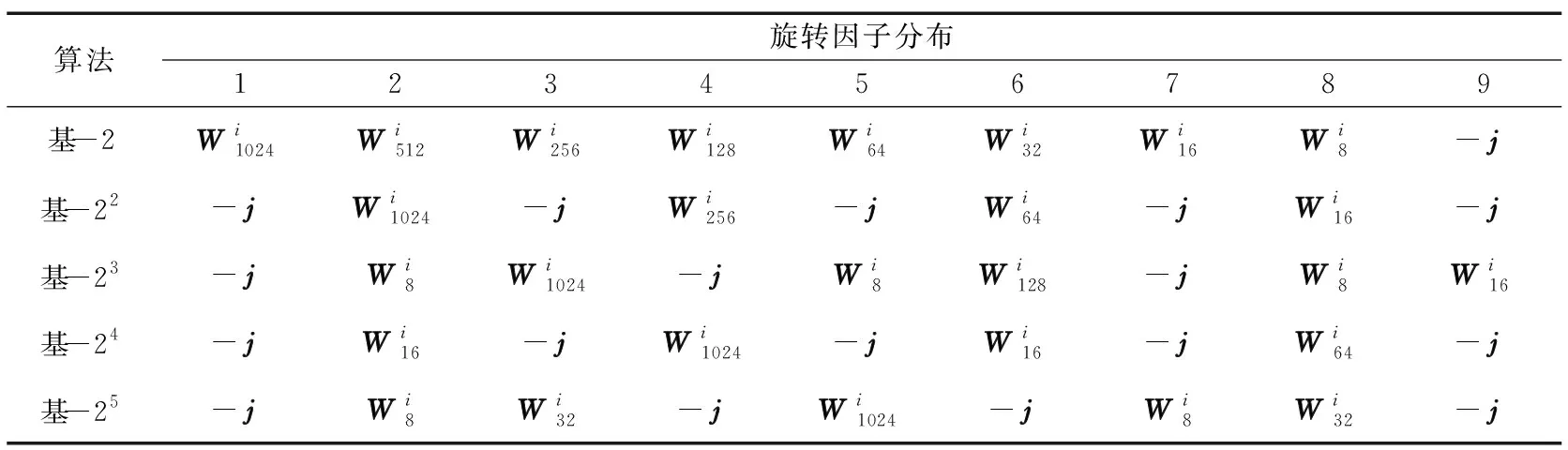
表1 1024點基-2k算法旋轉因子運算分布Tab.1 Distribution of twiddle factor at each stage to compute 1024-point FFT for radix-2k algorithm
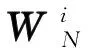
2 整體設計方案
圖1所示為基-25算法SDF架構1 024點FFT處理器的整體結構圖。圖1中,BF2I與BF2II模塊為基本的I型與II型蝶形單元,主要用于輸入復數序列的加法與減法運算,II型蝶形單元除了進行基本的加減法運算還要處理額外的‘-j’運算[14];蝶形單元上方的矩形塊為不同容量的延遲緩沖單元,主要為蝶形單元的輸入提供恰當的數據并對數據進行整理;‘?’代表復數乘法運算單元,輸入序列通過復數乘法單元運算后,就會得到與相應階段旋轉因子相乘的結果,計算后的結果會直接進入下一階段的蝶形運算中;‘CLK’為控制時鐘,由10位計數器產生,用于切換蝶形單元的類型并為復數乘法單元提供合適的控制邏輯。

圖1 基-25算法1024點SDF FFT結構圖Fig.1 Block diagram of radix-25 1024-point SDF FFT
2.1 旋轉因子拆分與兩階段CSD常數乘法
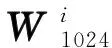
2.1.1 旋轉因子拆分原理
圖2所示為截取基-25算法64點FFT第5階段旋轉因子運算的信號流圖。
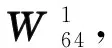
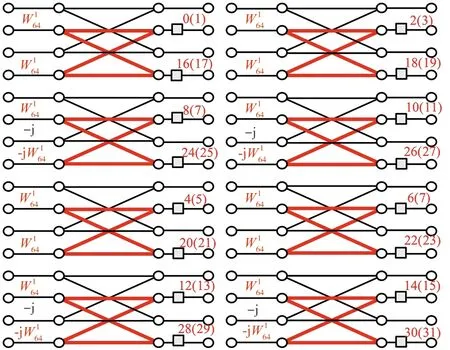
圖2 第5階段基-25算法64點FFT信號流圖Fig.2 SFG of radix-25 for 64-point FFT of the 5th stage
邏輯模塊
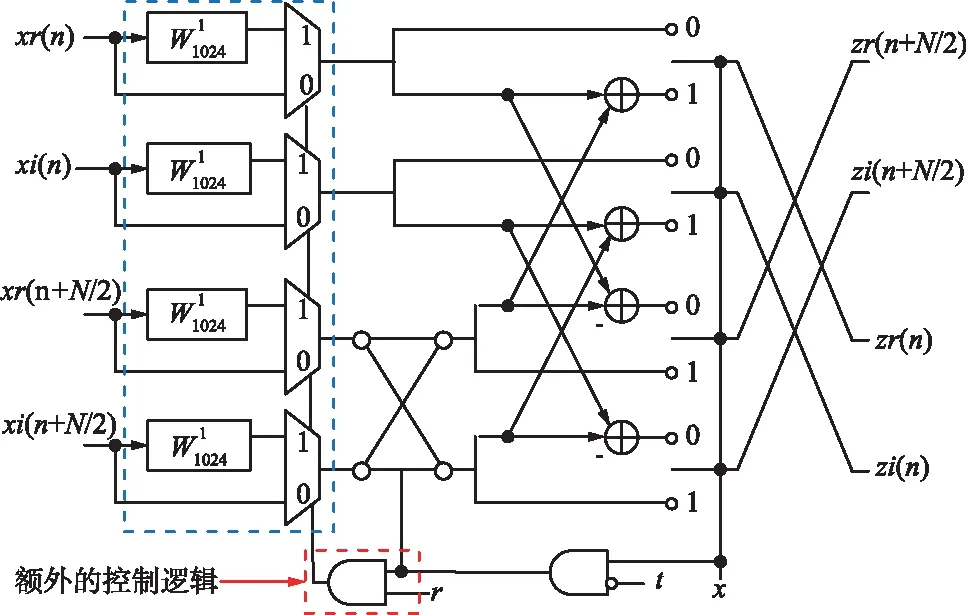
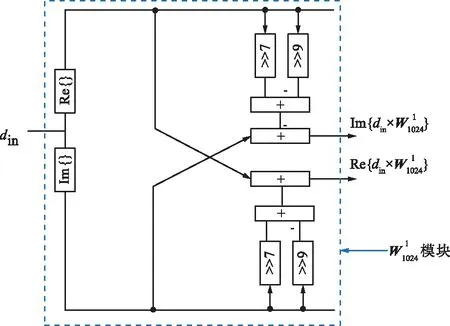
(b) 改良后的蝶形單元圖3 內嵌模塊的蝶形單元Fig.3 Butterfly unit with embedded
2.1.2 兩階段CSD常數乘法單元
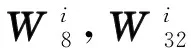

表2 8區域中旋轉因子對應的映射Tab.2 Eight symmetric region mapping of twiddle factor
(1)
CSE1=din+din>>2
CSE2=din-din>>2
CSE3=din+din>>3
CSE4=din-din>>3
CSE5=din-din>>4。
(2)
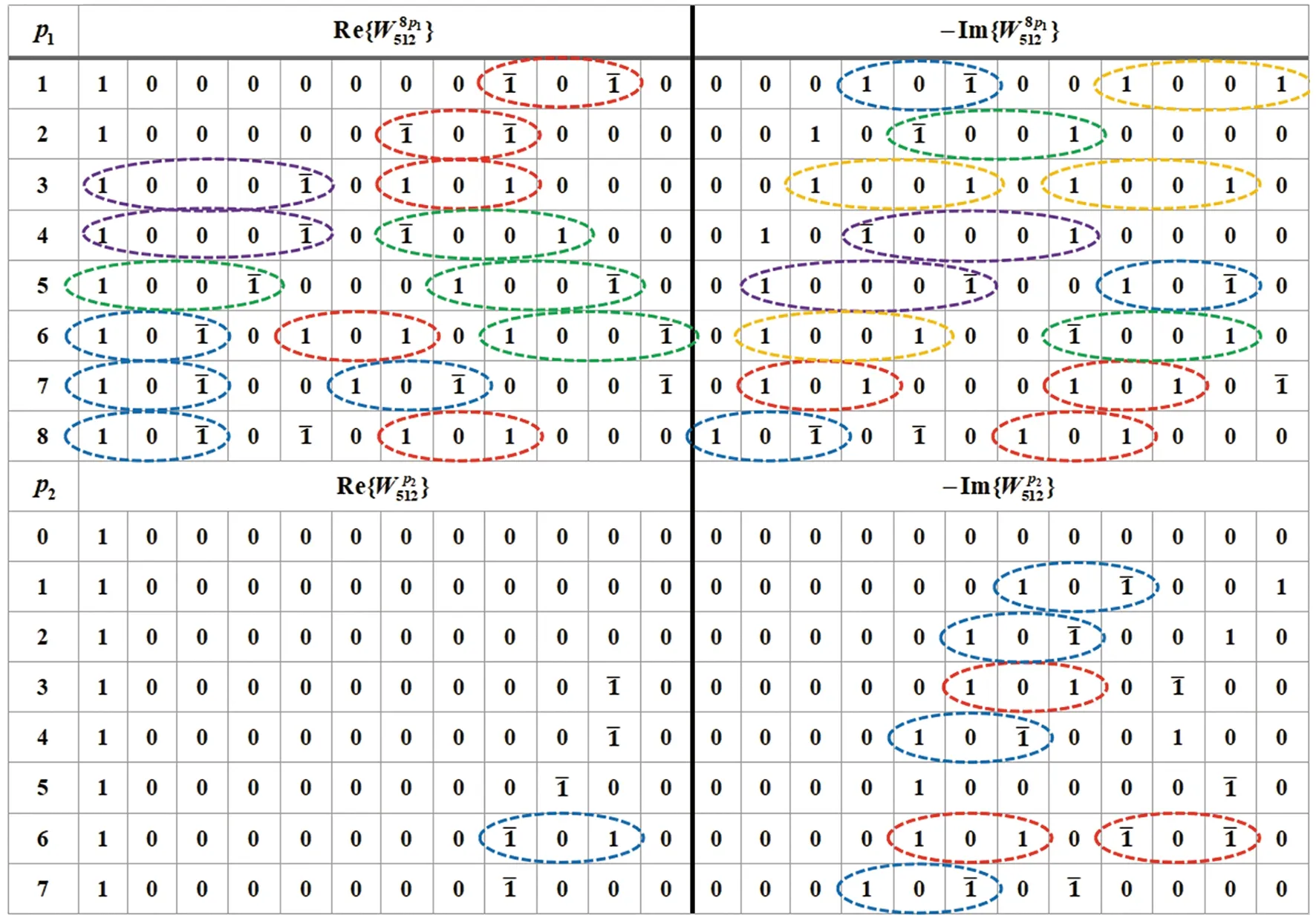
表3 12位字長16組常數值CSD數值表示Tab.3 CSD representation of sixteen constant values with 12-bit word-length
2.2 適配于與乘法單元
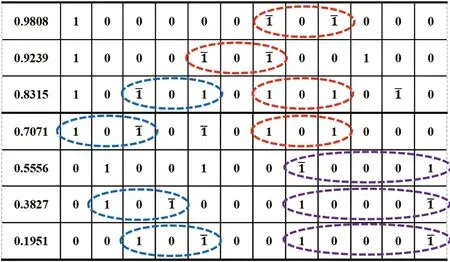
表4 7常數值CSD表示Tab.4 CSD representation of seven constant values
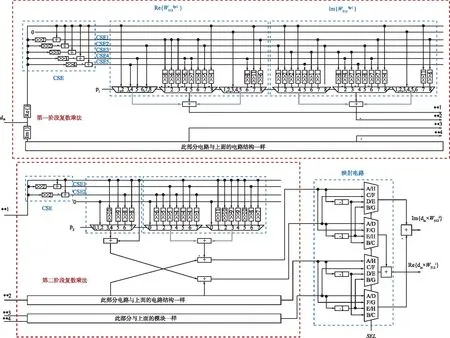
(a) 適配于旋轉因子兩階段CSD常數乘法單元邏輯模塊
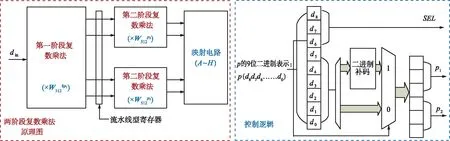
(b) 兩階段復數乘法及控制邏輯圖解圖4 適配于旋轉因子兩階段CSD乘法單元整體架構詳解Fig.4 Detailed overall architecture of two-stage CSD multiplied unit for twiddle factor
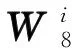
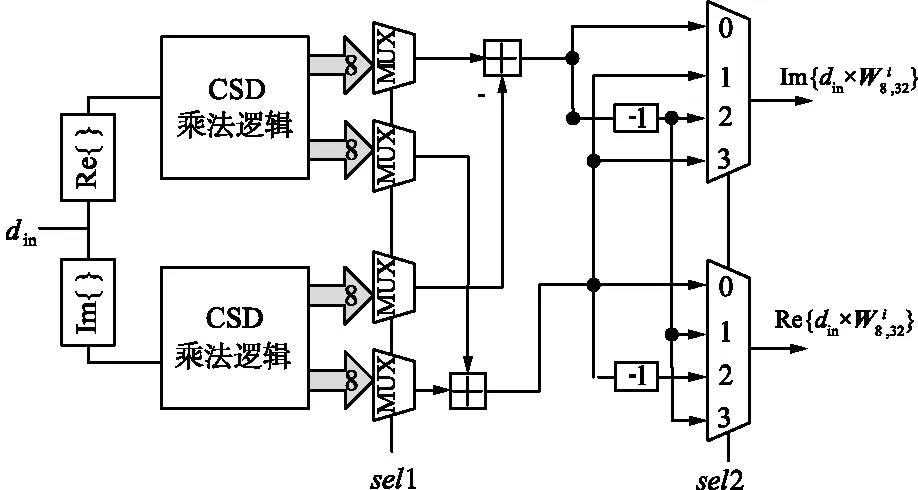
(a) CSD常數乘法單元通用架構
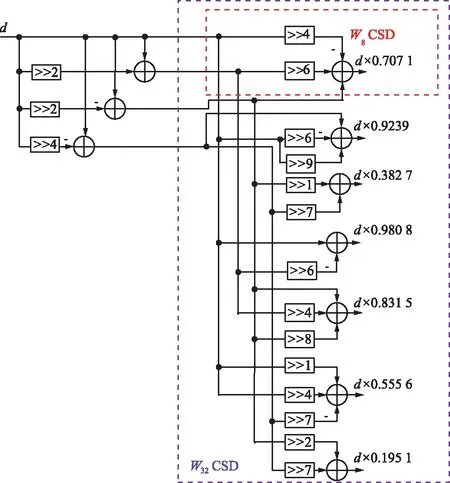
(b) 適配于與邏輯模塊圖與乘法單元Fig.5 CSD multiplied unit for
3 評估與比較
采用Verilog HDL對所設計的1 024點FFT處理器進行建模,利用QUARTUS PRIME開發平臺對設計進行綜合評估,器件選擇Intel FPGA CYCLONE家族的10CL055YU484I7G。表5所示為本文的設計方案與其他已存在的設計方案在1 024點FFT處理器設計方面的比較,為了更加直觀地評估各個方案的硬件資源消耗,對設計所消耗的LEs與MBs進行了標準化處理,設定本文方案的所消耗的LEs與MBs為1。
圖6所示為基于Matlab計算出的結果與QUARTUS PRIME平臺仿真工具MODELSIM-ALTERA得出結果之間的比較(設輸入序列的實部與虛部取值范圍為1~1 024),其中‘*’代表Matlab計算結果,‘△’代表MOELSIM仿真結果。
圖6中FFT點數的輸出結果表明,MODELSIM仿真結果與Matlab計算結果完全吻合,驗證了所提出設計方案的有效性。
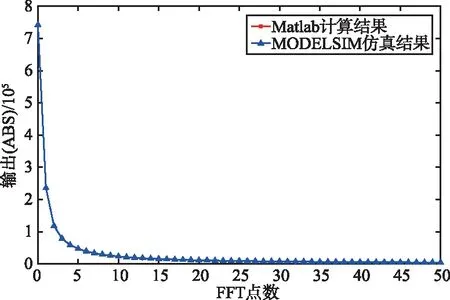
(a) 計算結果比較(FFT點數取值范圍0~50)
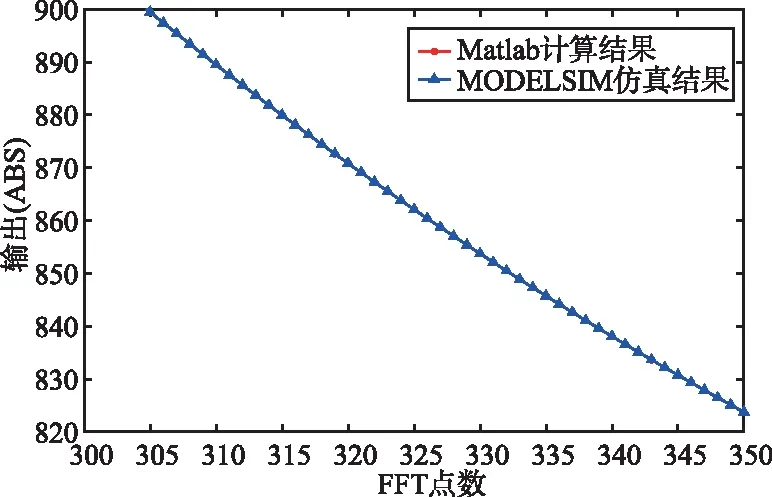
(b) 計算結果比較(FFT點數:取值范圍300~350)
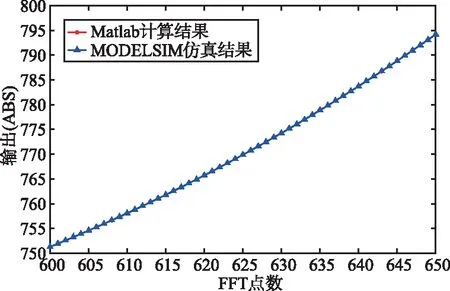
(c) 計算結果比較(FFT點數:取值范圍600~650)
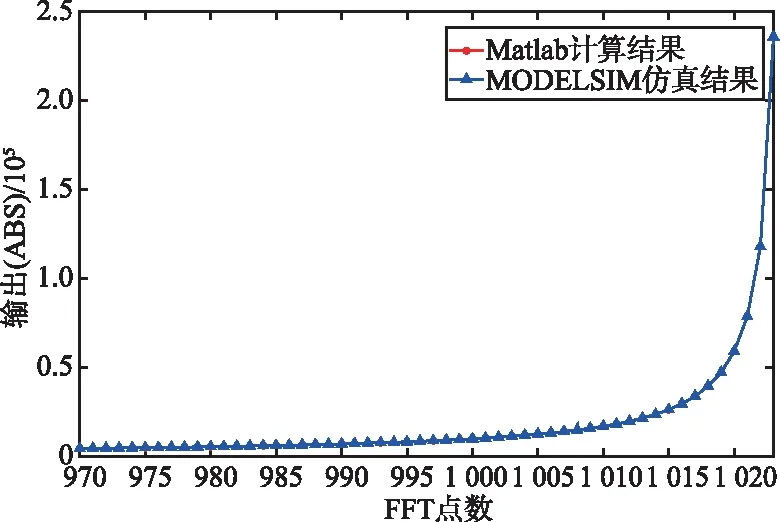
(d) 計算結果比較(FFT點數:取值范圍970~1 023)圖6 MODELSIM結果與Matlab計算結果比較Fig.6 Comparison between MODELSIM simulation result and Matlab calculation result
由表5可知,對比已存在的設計方案,本文的設計方案至少能夠節約28%的LEs與48%的MBs,工作頻率為120 MHz時功耗為12.6 mW。本文的設計方案內部字長設定為24 bit,SQNR達到了57.6 dB,同時本文無需布斯乘法器參與復數乘法運算,全部采用硬件資源消耗低的CSD常數乘法器來完成。

表5 不同方案1 024點FFT處理器性能比較Tab.5 Performance of the proposed 1 024-point FFT processoras compared with existing schemes
4 結束語
本文基于Intel FPGA設計了一種緊湊型1 024點FFT處理器,為了減少旋轉因子的復雜度,采用了基-25算法,考慮到硬件實現的難易度和硬件成本問題,使用了SDF流水線架構。在此基礎上提出了一種旋轉因子的分解方案,使得所有復數乘法運算全部由CSD常數乘法單元完成,大幅度地降低了硬件成本。基于QUARTUS PRIME綜合結果顯示,對比已有的方案能夠至少節約28%LEs和48%MBs的使用量,SQNR達到了57.6 dB,工作頻率為120 MHz時,功耗為12.6 mW,本文所設計的1 024點FFT處理器非常適合對硬件成本和功耗要求苛刻的應用場景。

