基于橢圓函數展開法求Klein-Gordon方程的行波解

韓冰冰

（盤錦職業技術學院 基礎部，遼寧 盤錦 124000）

近年來，非線性方程在自然科學與工程應用方面占據非常重要的地位。其中求解非線性方程的精確解是一項具有重要現實意義的科研工作[1]。同時，非線性方程解的唯一性問題一直都是科研工作者的關注熱點[2]。尤其是求解非線性方程的方法有很多，包括雙曲正切函數展開法[3]、sine-cosine方法[4]、齊次平衡法[5]以及試探函數法[6]等。盡管這些方法能夠求解非線性方程的孤波解或者沖擊解，但對于周期解的解析并不是都適宜[3-6]。針對這一問題科研工作者提出了許多新的求解方法。例如，楊娟等人通過Riccati展開法和復變換獲得非線性分數階Sharma-Tasso-Olever方程和時空分數階耦合Burgers方程的精確解[7]。熊淑雪等人利用復變換和整合分數階導數方法求出了分數階JM方程的新精確解[8]。王輝采用tanh函數方法對耦合Kaup-Kupershmidt方程求解，通過行波約化和Riccati方程進行方程轉化最終求得顯式行波解[9]。目前，尋找非線性方程新形式的精確解仍然是一件很有意義的工作。為尋求非線性Klein-Gordon方程的更多的周期解，將Jacobi橢圓函數展開法作進一步推廣，得到了該方程許多豐富的行波解，然后通過參數取值得到了該方程的一些特殊的精確解，包括三角函數解、雙曲函數解及它們的混合解，使以前的一些結論得到了有效推廣。

1 Jacobi橢圓函數的概述

1.1 Jacobi橢圓函數的性質

Jacobi橢圓函數的定義和性質可以參看文獻[10]，其中sn（ξ,k）稱為Jacobi橢圓正弦函數，cn（ξ,k）稱為Jacobi橢圓余弦函數，dn（ξ,k）稱為第三類Jacobi橢圓函數，用到Jacobi橢圓函數的以下性質：

1.1.1 轉化關系

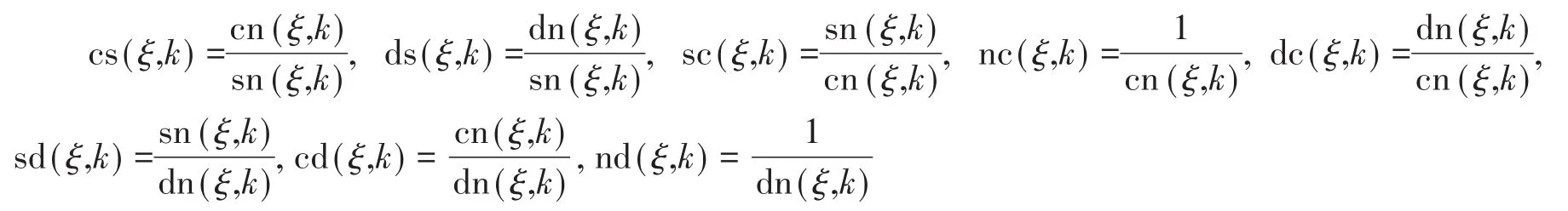
1.1.2導數關系

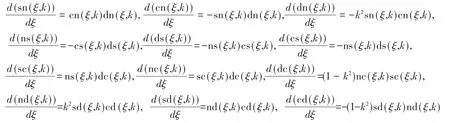
1.1.3 平方關系

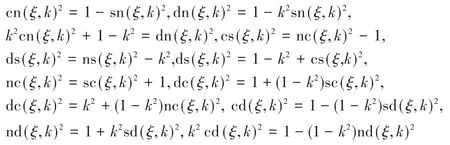
1.1.4 極限關系

當k→0時：

sn（ξ,k）=sin（ξ）,cn（ξ,k）=cos（ξ）,dn（ξ,k）=1,

ns（ξ,k）=csc（ξ）,cs（ξ,k）=cot（ξ）,ds（ξ,k）=csc（ξ）,

sc（ξ,k）=tan（ξ）,nc（ξ,k）=sec（ξ）,dc（ξ,k）=sec（ξ）,

sd（ξ,k）=sin（ξ）,cd（ξ,k）=cos（ξ）,nd（ξ,k）=1

當k→1時：

sn（ξ,k）=tanh（ξ）,cn（ξ,k）=sech（ξ）,dn（ξ,k）=sech（ξ）,

ns（ξ,k）=coth（ξ）,cs（ξ,k）=csch（ξ）,ds（ξ,k）=csch（ξ）,

sc（ξ,k）=sinh（ξ）,nc（ξ,k）=cosh（ξ）,dc（ξ,k）=1,

sd（ξ,k）=sinh（ξ）,cd（ξ,k）=1,nd（ξ,k）=cosh（ξ）

其中0≤k≤1是Jacobi橢圓函數的模數。

1.2 Jacobi橢圓函數的展開法

非線性發展方程的一般形式可寫為

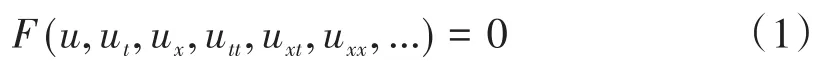
式中的F是關于變元u,ut,ux,utt,uxt,uxx,...的多項式。引入行波變換

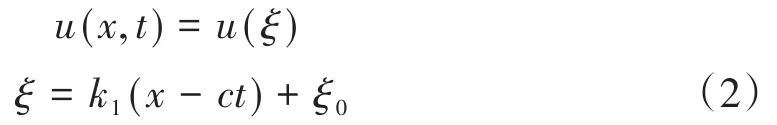
其中k1和c是非零的待定常數，ξ0是任意常數。將（2）代入（1）得到關于u（ξ）的常微分方程

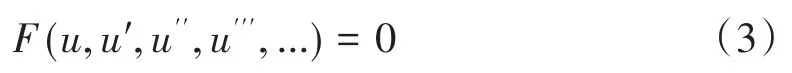
設方程式（3）具有如下形式的行波解

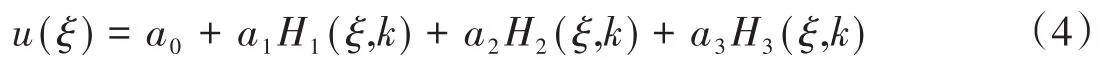
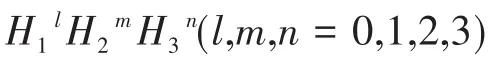
2 Klein-Gordon方程的其他形式的解

2.1 Klein-Gordon方程的行波解

考慮非線性Klein-Gordon方程

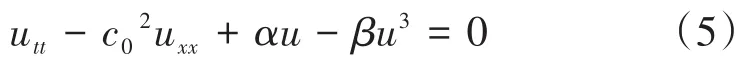
將式（2）代入式（5）,整理得到

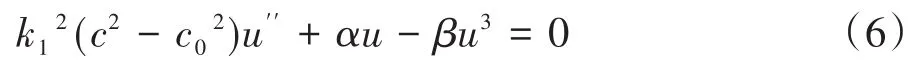
將式（4）代入式（6）。當Hi（ξ,k）選取不同的Jacobi橢圓函數時，計算得到不一樣的非線性Klein-Gordon方程行波解。本研究根據以下4種情形進行計算：

2.1.1 情形一

令H1（ξ,k）=sn（ξ,k）,H2（ξ,k）=cn（ξ,k）,H3（ξ,k）=dn（ξ,k）時，得到

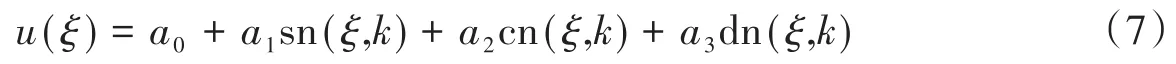
對式（7）求二階導數得到

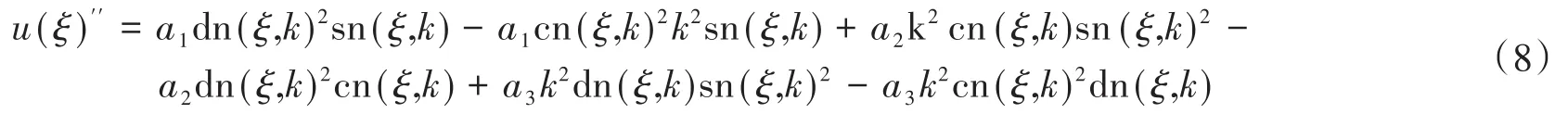
對式（7）求立方得到

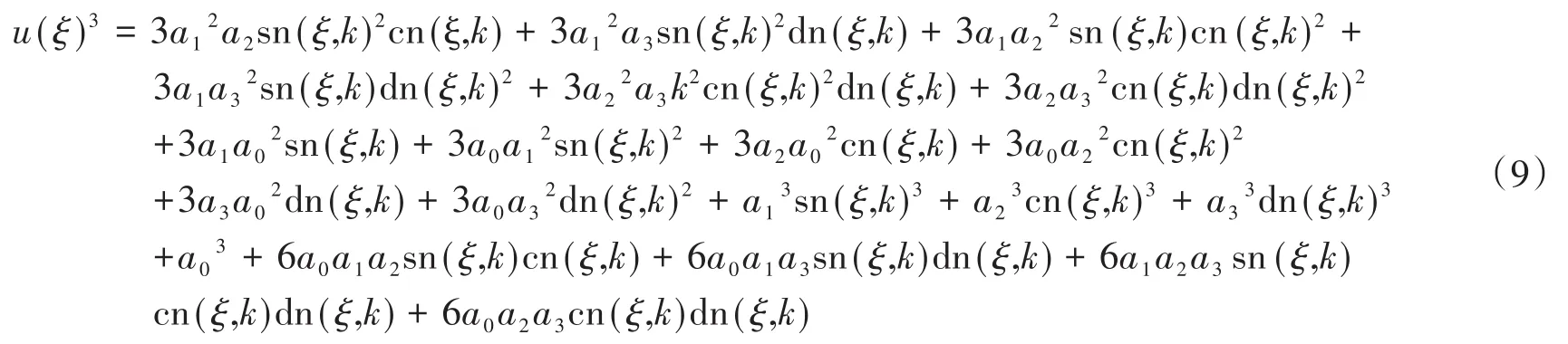
將式（7）、式（8）、式（9）同時代入式（6）整理得到

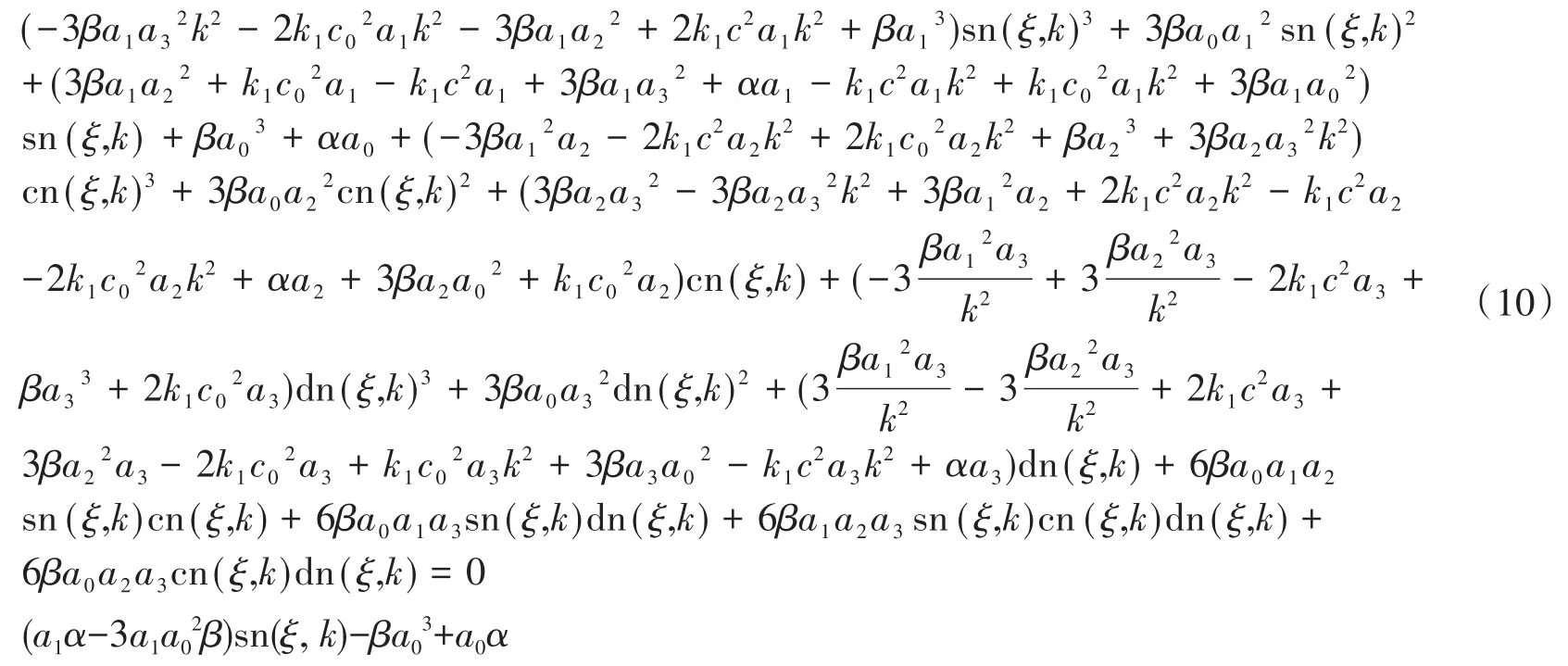
在式（10）中令sn（ξ,k）lcn（ξ,k）mdn（ξ,k）n（l,m,n=0,1,2,3）系數均為零，解得式（5）的以下六個解：

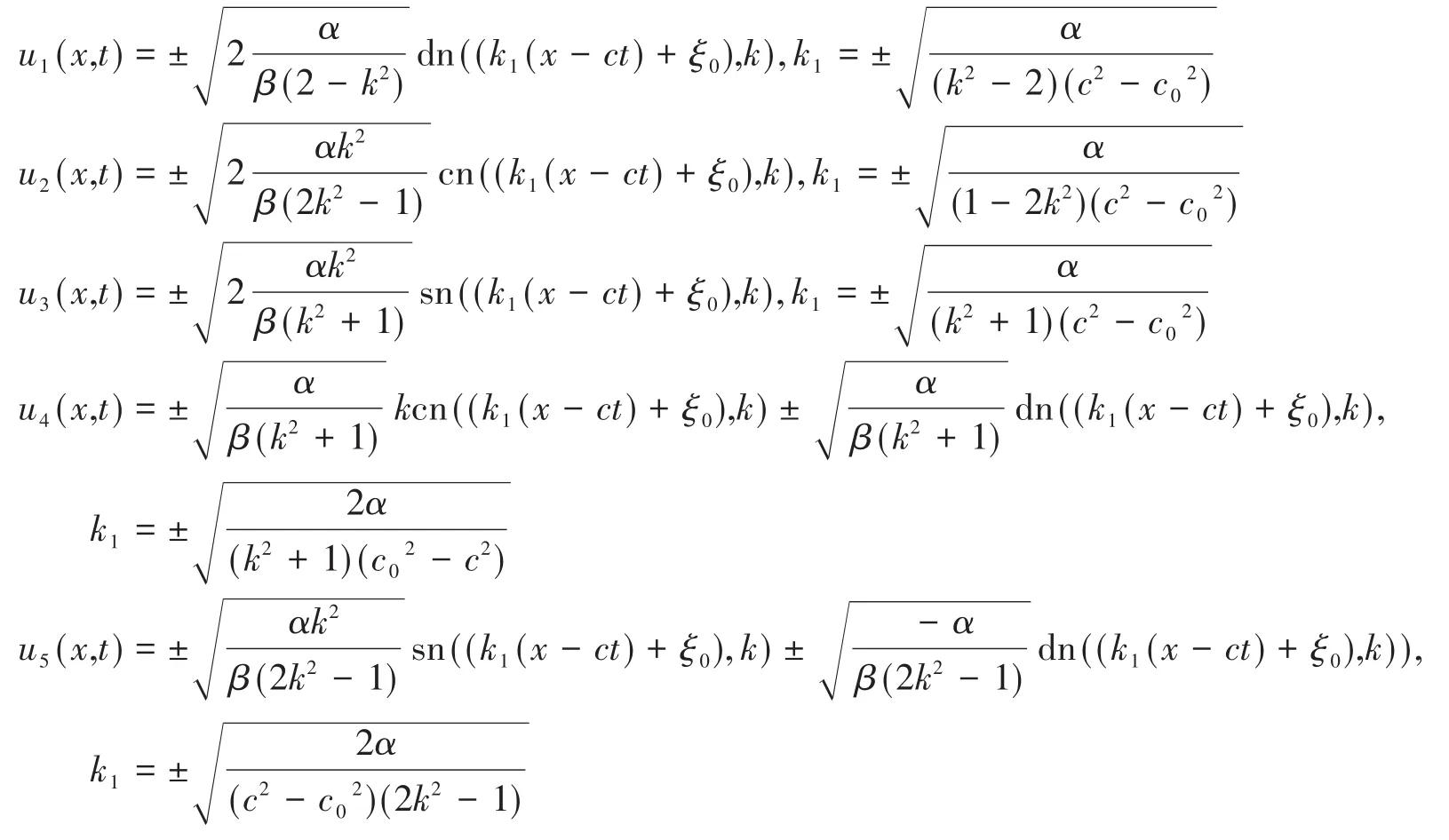
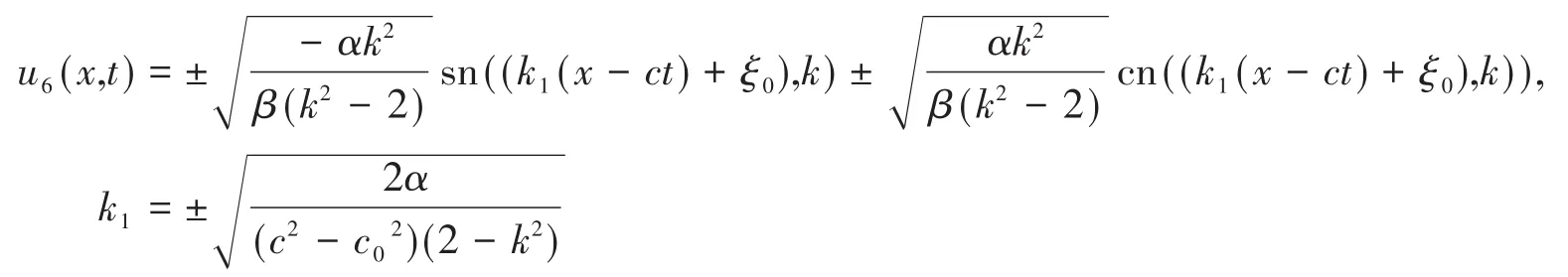
2.1.2 情形二

令H1（ξ,k）=sd（ξ,k）,H2（ξ,k）=cd（ξ,k）,H3（ξ,k）=nd（ξ,k）時，得到

u（ξ）=a0+a1sd（ξ,k）+a2cd（ξ,k）+a3nd（ξ,k）

按照情形一的計算步驟，計算得到以下六個式（5）的解：

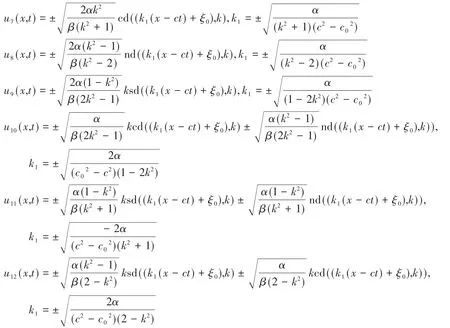
2.1.3 情形三

令H1（ξ,k）=ns（ξ,k）,H2（ξ,k）=cs（ξ,k）,H3（ξ,k）=ds（ξ,k）時，得到

u（ξ）=a0+a1ns（ξ,k）+a2cs（ξ,k）+a3ds（ξ,k）

按照情形一的計算步驟，計算得到以下六個式（5）的解：

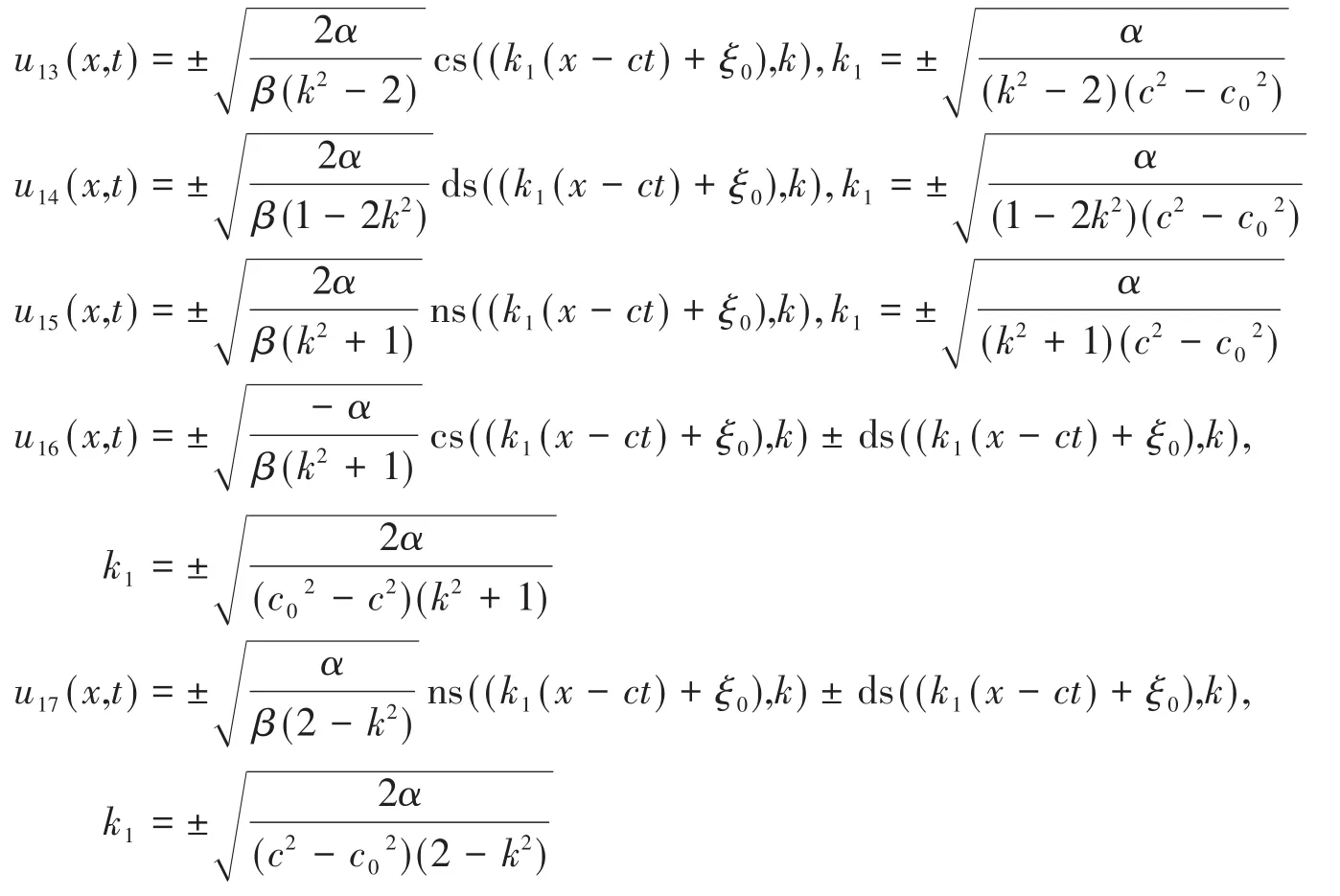
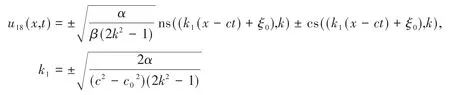
2.1.4 情形四

令H1（ξ,k）=sc（ξ,k）,H2（ξ,k）=nc（ξ,k）,H3（ξ,k）=dc（ξ,k）時，得到

u（ξ）=a0+a1sc（ξ,k）+a2nc（ξ,k）+a3dc（ξ,k）

按照情形一的計算步驟，計算得到以下六個式（5）的解：

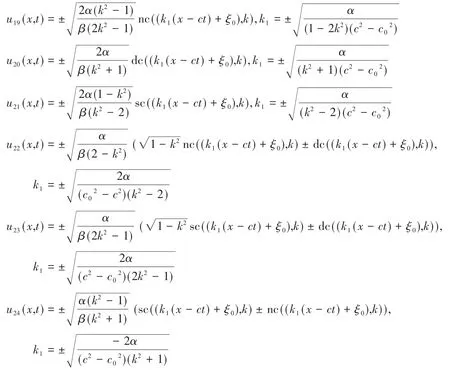
根據所求得的行波解，利用Maple 7軟件繪制解的波形圖。以u1（x,t）圖形為例，u1（x,t）的波形圖見圖1。

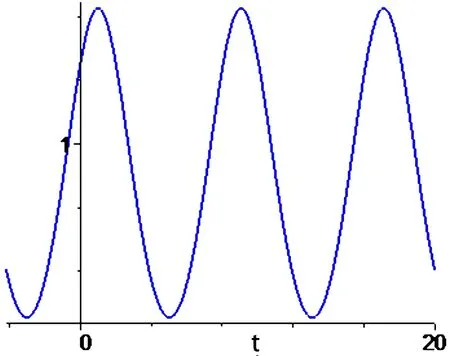
圖1 解u1（x,t）的波形圖：ξ0=0,c0=2,α=1,β=1,c=1,k=,x=1

2.2 Klein-Gordon方程的其他形式的解

上述得到的非線性Klein-Gordon方程的24個行波解，如果考慮它們的極限情況，即當k→1時，Jacobi橢圓函數退化為雙曲函數；當k→0時，Jacobi橢圓函數退化為三角函數。

2.2.1情形一

當k→0時，非線性Klein-Gordon方程，即式（5）的24個行波解退化為以下三角函數形式的解：

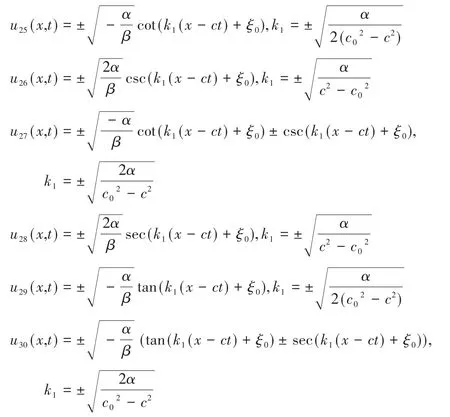
2.2.2 情形二

當k→1時，得到的非線性Klein-Gordon方程（5）的24個行波解退化為以下雙曲函數形式的解：

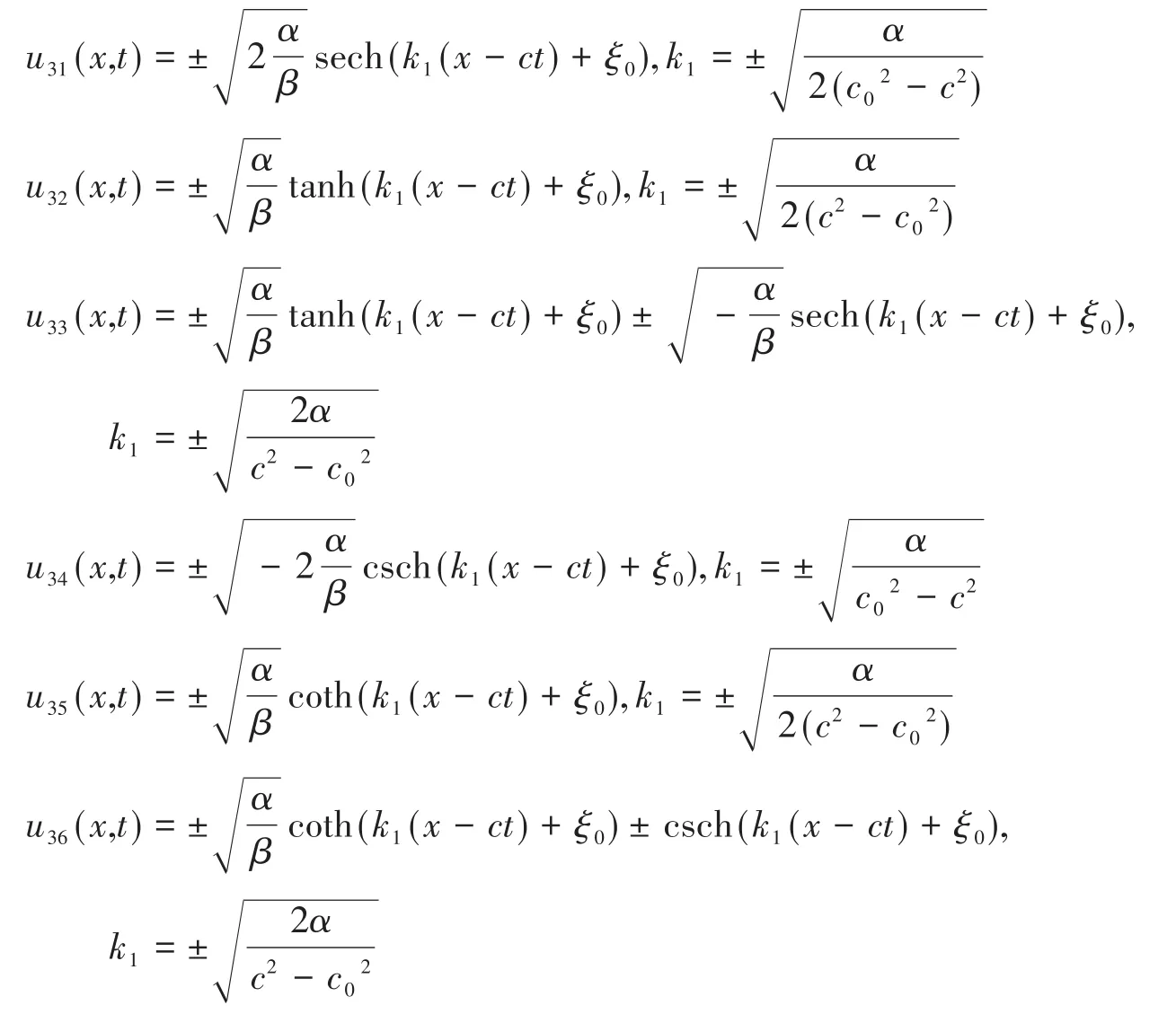
3 結論

本研究以Klein-Gordon方程為例，介紹了Jacobi橢圓函數的性質和展開法，利用該方法求得非線性Klein-Gordon方程一系列新的精確周期解，并且充分考慮到極限情況，得到的三角函數及雙曲函數的解，從而揭示了求解非線性Klein-Gordon方程精確行波解的理論和技巧。此外，該方法具有一定的普遍性，可以用來求解更多的非線性發展方程，例如非線性Schrodinger方程、KP方程、Ginzburg-Landau方程等。