光纖模場直徑測量的兩段多項式函數擬合法

陶嘉慶，胡 越，項華中，涂建坤，鄭 剛

(1.上海理工大學 上海介入醫療器械工程研究中心,上海 200093;2.上海電纜研究所,上海 200093)

光纖是具有細長圓柱狀光波導結構，主要由纖芯、包層及涂覆層3部分組成[1]。單模光纖傳輸的光能量不僅在纖芯內，還有一部分分散在包層。所以單模光纖的傳輸特性不能簡單地由纖芯直徑表示。模場直徑表示光纖基模(LP01模)中電場的分布情況[2]。通過模場直徑，可以了解到光纖的部分重要特性，例如彎曲損耗[3]和色散特性[4]，并且根據模場直徑隨波長的變化譜還可推導出等效階躍光纖的構成等重要參數[5]。

我國關于模場直徑測量的現行標準[6]推薦了4種測量方法，分別是直接遠場掃描法[7]、遠場可變孔徑法[8]、近場掃描法[9]和光時域反射計的雙向后向散射法[10]。前3種方法都是基于Petermann第二定義得出的，在一定條件下可以相互轉化。此外，文獻[11]運用低相干度交互測量法測量光纖的模場直徑。文獻[12]用高階高斯分布逼近光纖中高階模電場分布。該方法可以測量出任意階高階模高斯光斑大小，進而得出與之對應的模場直徑。本文采用上海電纜研究所生產的OFM光纖測量儀進行模場直徑的測量。OFM光纖測量儀已在國內的幾個光纖生產大廠使用，其利用遠場可變孔徑法測量模場直徑[13]。一般情況下，可變孔徑法所需的開孔數較多(20個孔徑以上)，通過電機轉動得到透過每個孔徑的一組光功率值。由于該測量是機械轉動，故整個測量過程需要一定的時間。本課題組通過使用單個多項式函數擬合光功率數據的方法，提高了儀器的重復測量穩定性[14]。考慮到光在光纖中的實際傳播模式，本文使用兩段多項式函數對測得的光功率數據進行擬合。在滿足測量精度的前提下，本方法可較好地減少遠場孔徑法的有效孔徑數，從而提升儀器的測量速度，降低生產成本，提高測量效率，滿足光纖生產廠家在生產現場質控中的實際需求。

1 模場直徑的測量和計算方法

OFM光纖測量儀測量光纖模場直徑時，采用了遠場可變孔徑法，該方法原理如圖1所示。

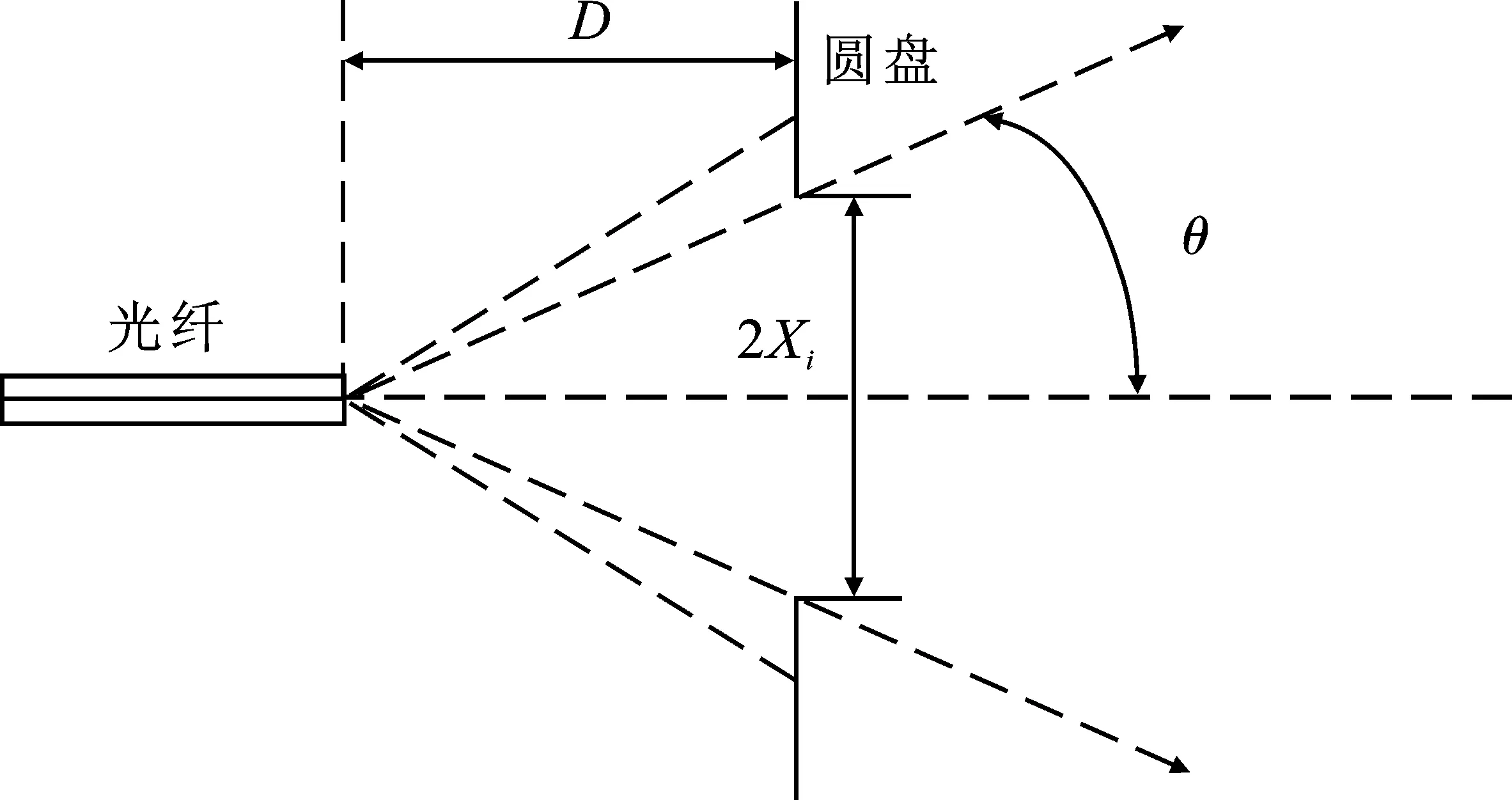
圖1 遠場可變孔徑法測量原理圖Figure 1. Measurement principle of far field variable aperture method

該儀器在一個圓盤上開有均勻分布的大小不同的20多個孔徑光闌。光纖端面到圓盤的距離為D。設第i個孔的直徑為2Xi，對應的遠場半角為θ，光纖軸心與孔的圓心位于同一直線。測試時，儀器會自動控制每個孔旋轉到與光纖軸心同軸的位置，同時測量通過該孔的遠場光功率并記錄。

根據國標[6]中規定的遠場可變孔徑法的測量原理，在Petermann第二定義[15]的基礎上，定義模場直徑的計算式為

(1)

式中，λ為波長，單位為納米(nm)；x為孔徑光闌半徑，單位為毫米(mm)；D的單位為毫米(mm)；α(x)為歸一化光功率。

經三角變換后，該式變為

(2)

(3)

由數值積分定義，式(2)可以用無限個小矩形來表示

(4)

則

(5)

只要精確測得遠場光功率的數值，便可計算得到模場直徑的值。

2 兩段多項式函數擬合法測模場直徑

2.1 兩段多項式函數擬合的提出

單模光纖在大于截至波長時只傳輸基模LP01模，而基模場分布在纖芯取零階貝塞爾函數，在包層取零階修正的貝塞爾函數，故模場分布一般沒有明確的分界線[16]。一般來說，纖芯中傳遞大約80%的光能量，其余20%的光能量在包層中傳遞[17]。纖芯中傳遞的能量用計算式表示為

P(θcore)=P(θmax)×80%

(6)

其中，P(θcore)為纖芯中的近似光功率；P(θmax)為光纖傳遞的全部光功率。

通過測量得到一組遠場孔徑角與歸一化光功率之間關系的離散數據點，如圖2所示。用與實測P(θcore)值相對應的第i個孔徑作為光在纖芯和包層中傳遞的分段點，本實驗中得到的分段點處遠場孔徑角近似為0.08 rad。

一般來說，擬合階數越高，擬合曲線越能經過大多數據點，但曲線平滑性較差。而較低的擬合階數下，曲線較為光滑，與高斯分布曲線較為接近，計算量也較小[18]，因此本文使用較低的擬合階數擬合大部分點。在對這些數據進行多次不同階次的多項式擬合實驗后，得到經驗擬合式如下所示

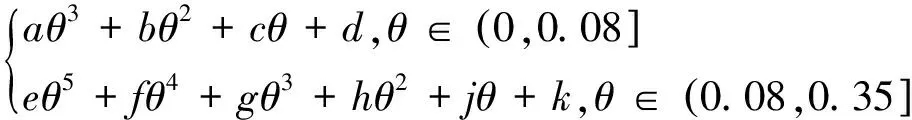
(7)

式中，a,b,c,…,k為多項式的系數。根據此式， 函數α(θ)在纖芯內用3階多項式擬合，在包層中用5階多項式擬合。

2.2 實驗結果及分析

實驗中用到的孔徑數為20個，遠場半角的范圍為0.02～0.35 rad。對式(3)分析后，加入積分下限：當半角為0 rad時，歸一化光功率α(θ)為1。實驗中選用的光纖為G652單模光纖，OFM光纖測量儀測得的模場直徑為9.20±0.02 μm。在測試波長數值為1 310 nm的條件下，共采集了5組遠場光功率數據，利用式(7)進行分段擬合。

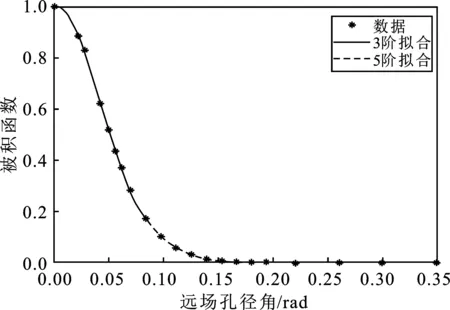
對其中的一組數據，其遠場孔徑角與歸一化光功率之間的關系曲線如圖2(a)所示。

(a)

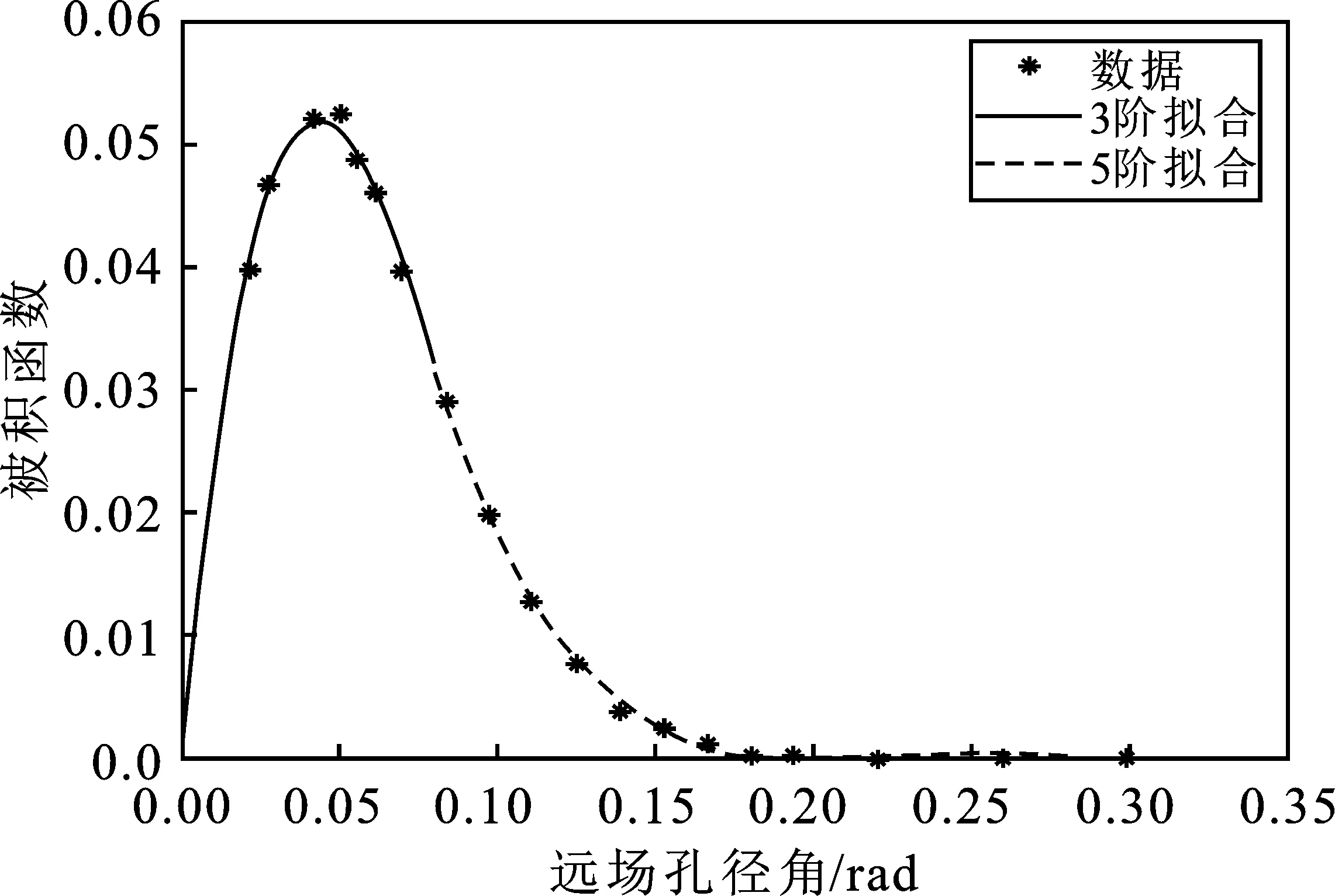
(b)圖2 G652光纖兩段多項式函數擬合曲線(a)歸一化光功率與遠場孔徑角關系曲線(b)被積函數與遠場孔徑角關系曲線Figure 2. Fitting curve of two-segments polynomial function of G652 optical fiber(a)Relation curve of normalized optical power and far field aperture angle(b)Relation curve of integrand function and far field aperture angle

用式(4)計算時，被積函數(α(θ)sin(2θ))與遠場孔徑角的關系如圖2(b)所示。

根據式(2)，將式(7)代入可積分計算出模場直徑的值WVAT。將其與OFM測量儀得到的模場直徑WOFM對比，結果如表1所示。

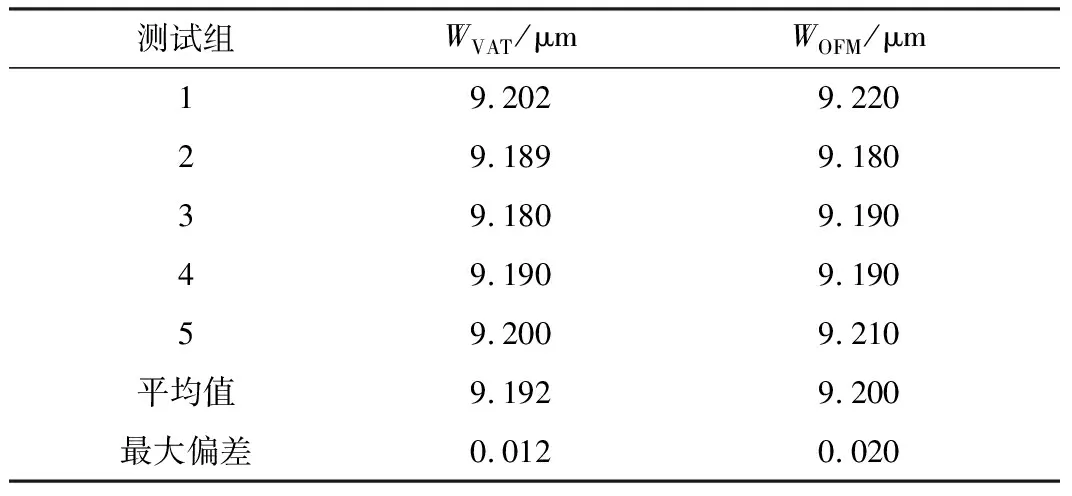
表1 兩段多項式擬合的測量結果

從表1可以看出，兩段多項式函數擬合法的計算結果與儀器測量結果一致，并由最大偏差值可以看出兩段多項式函數擬合法測量模場直徑時有較好的重復測量(精度)穩定性。

2.3 測量數據誤差及處理

實驗過程中可能會出現由電機轉動引起的孔徑光闌圓心未能與光纖軸心位于同一直線的情況，導致透光光闌的光功率不能被完全接收，使得某1～2個孔的測量值與實際值有偏差。選某組測量有兩個誤差點的一組數據，擬合如圖3所示。

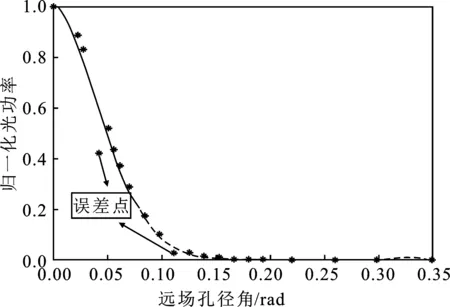
圖3 兩個誤差點時遠場孔徑角與歸一化光功率的擬合曲線Figure 3. Fitting curve of far-field aperture angle and normalized optical power for two error points

從圖3可以看出，誤差點的存在影響了曲線的擬合，導致曲線向誤差點偏移。此時得到WVAT=9.301 μm，與儀器測量值WOFM=9.20 μm差異較大。為了消除這兩個誤差點的影響，本文采用再次擬合的方法：在θ∈(0,0.08]范圍內設置一個閾值常數k1，在θ∈(0.08,0.35]范圍內設置一個閾值常數k2，若擬合曲線上的點與對應實測數據點之差的絕對值t小于k1或k2，則返回此點對應的坐標，將橫坐標遠場孔徑角與縱坐標歸一化光功率一起刪除。再次擬合曲線如圖4所示。

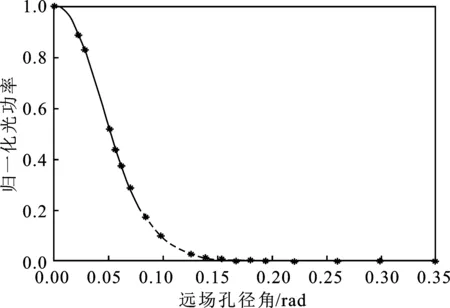
圖4 刪除誤差點后遠場孔徑角與歸一化光功率的擬合曲線Figure 4. Fitting curve of far-field aperture angle and normalized optical power after deletion of error points

運用式(2)～式(5)，得到模場直徑為WVAT=9.205 μm，與實測值的誤差僅為0.005 μm。由此結果可知當孔徑數較多且存在測量誤差時，可使用再次擬合的方法去除誤差點，從而使計算結果更接近實際值。

3 測量孔徑數的優化實驗

通常，遠場可變孔徑法用到的測量孔數有20余個，而國際電信聯盟電信標準分局發布的最新標準規定測量孔徑至少為12個[19]。從理論上來說，孔徑越密集，遠場可變孔徑角間隔越小，可更加精確地計算出被測單模光纖的模場直徑。但孔徑數過多會增加測試儀成本，導致測量效率下降。因此，需要選用較為合理的孔徑光闌分布及數量，使其滿足測量精度的要求，又可以提升測量效率。

3.1 孔徑設置方法

實驗中選取G652以及G655型(其模場直徑為7.78±0.02 μm)的單模光纖兩組各5根。在測試波長為1 310 nm時，每根測量1次共得到兩組各5個數據。兩段多項式函數擬合法運用于本實驗時，為使方程有合理解，對應5階多項式函數擬合，至少需要6個點；對應3階多項式函數擬合，至少需要4個點。故擬合使用到的數據點數至少為10個。經多次擬合實驗，在不改變OFM測量儀結構的基礎上，選取下列孔徑：選用于3階函數擬合的為第1、3、7、8個孔；用于5階函數擬合的為第8、10、12、16、18、19、20個孔。其中第8孔徑為共用過渡孔，總共取10個孔徑。

3.2 測試結果及分析

本文采用10個孔的測量值進行多項式擬合。對光纖G652和G655的某一根歸一化光功率擬合曲線如圖5(a)所示，被積函數曲線如圖5(b)所示。圖中的“*”和“○”為相應的采集數據，實線為3階擬合，虛線為5階擬合。

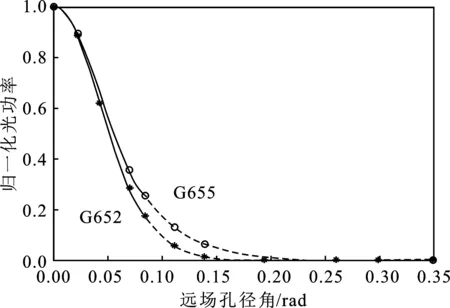
(a)

(b)圖5 10孔擬合下兩種光纖的光功率分布及被積函數曲線(a)歸一化光功率與遠場孔徑角關系曲線(b)被積函數與遠場孔徑角關系曲線Figure 5. Optical power distribution and integral curves of two kinds of optical fibers with 10 holes fitting(a)Relation curve of normalized optical power and far field aperture angle(b)Relation curve of integrand function and far field aperture angle

從圖5可以看出，兩種光纖的擬合曲線均較為平滑，實驗計算結果如表2和表3所示。

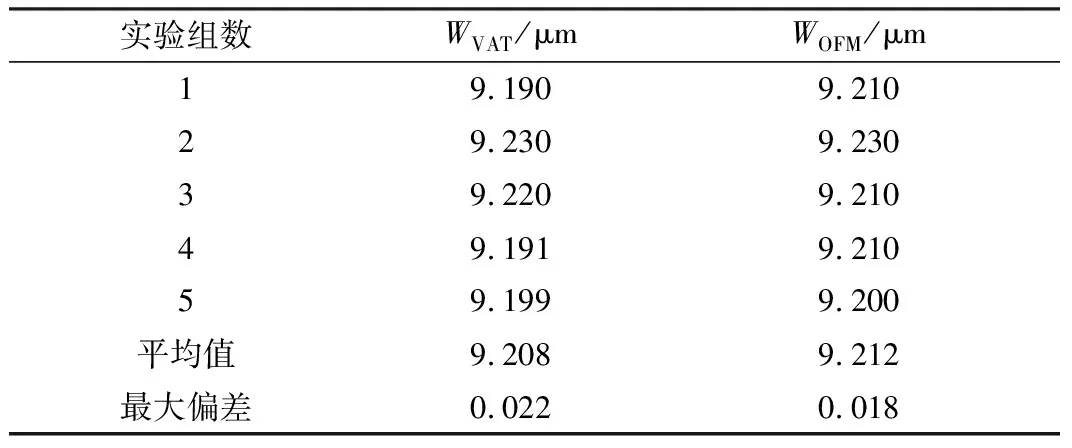
表2用10個孔擬合得到的模場直徑及與OFM儀的測量值比較 (G652光纖)

表3 用10個孔擬合得到的模場直徑及與OFM儀的測量值比較(G655光纖)

從表2和表3可看出，無論是G652還是G655光纖，用式(7)擬合后，計算結果重復性較好。盡管10孔實驗的測量結果的最大偏差仍略大于儀器測量結果的偏差(儀器測量時仍采用20個孔徑)，但該誤差在允許范圍內。因此，本文將基于遠場可變孔徑法測量光纖模場直徑的兩段多項式函數擬合法的最少孔徑數設置為10個孔。

4 結束語

光纖的模場直徑表示光纖光能量的集中程度。準確快速地測量模場直徑對于光纖的生產具有重要的實際意義。由于光纖在纖芯和包層中模場分布存在不同，本文提出采用兩段多項式函數擬合法用于(基于遠場可變孔徑法的)模場直徑測量。實驗結果表明，該方法在20孔測量模場直徑時有很好的重復測量穩定性。在保證測量精度的前提下，使用本文所提方法可有效減少測量所需的孔徑數至10孔，提升了儀器的測量效率。本文的不足之處在于未能確定纖芯和包層明確模場分界，沒有從理論上推導出明確的分段點，這也是下一步的研究重點。