分布定位式光纖振動傳感系統的事件識別

吳世海，任梓豪，何抒航，賈建華，孟雨盈，孔 勇

(上海工程技術大學 電子電氣工程學院，上海 201620)

0 引 言

由于相位敏感光時域反射計(φ-OTDR)[1-2]具有高靈敏度、高空間分辨率、監控距離長的優勢，可以準確的定位振動事件位置。所以，φ-OTDR分布式聲傳感器已被廣泛應用于油氣管道安全檢測[3]、高速軌道的入侵檢測[4]、周界安防[5]等領域。但是，在這些領域對于識別實際環境下的振動事件還是非常具有挑戰性的任務。

對振動信號的識別主要分為3個步驟：振動信號的預處理、振動信號的特征提取、對振動信號進行分類。振動信號的預處理主要是對信號進行去噪，劃分數據集；特征提取需要通過不同方式來獲取不同類型的振動信號特征。提取到的特征應能很好的表達振動信號具有的性質，不同特征之間的搭配也會形成不同的分類效果。提取的典型特征有短時過零率、短時能量、梅爾頻率倒頻系數(MFCC)[6-8]。除了直接提取特征外，還可以使用EMD、VMD分解算法將信號分解后再提取信號的相關特征[9-10]。根據提取的振動信號的特征使用分類器進行分類。典型的分類器有支持向量機(SVM)[11]、相關向量機(RVM)[12]、高斯混合模型[13]和隨機森林樹[14]。然而在使用分布式光纖傳感系統進行長距離監測時，數據量會隨監測長度的增加而增加，但上訴方式在處理大量數據時會非常耗費時間。對于振動信號特征的選擇也是一件很困難的事情，對于不同類型的振動事件使用相同的特征可能會出現識別效果不理想的情況。

隨著深度學習算法在圖像識別[15]、情緒識別[16]、故障診斷[17]中的應用，深度學習算法也開始被應用到對分布式聲傳感器振動信號的識別中。文獻[18]中提出，將卷積神經網絡應用到分布式光纖聲傳感系統中，去識別電纜的放電現象。使用的方式為：使用梅爾頻率倒譜算法，將采集到的電纜一維振動信號轉為二維的MFCC后，根據得到的MFCC畫出二維圖像；將該MFCC圖像作為深度神經網絡的輸入，使識別平均準確率達到97.1%。文獻[19]提出使用一維卷積神經網絡代替二維卷積神經網絡，在降低識別時間的同時提高了識別準確率。文獻[20]提出使用兩種不同類型的卷積神經網絡，對高速軌道的入侵事件進行檢測，克服了大量噪聲的影響，將誤報率減小到10%，準確率到達了91%。雖然這些方法提供了很好的結果，但為了提高在實際環境下的識別準確率，仍然需要開辟新的方式。

因此，本文嘗試使用雙輸入多層卷積神經網絡(TI_CNN)對振動事件進行分類。首先將經過小波包去噪的原始信號輸入1-D CNN，把通過小波變換得到的小波時頻圖輸入2-D CNN中；將1-D CNN和2-D CNN提取的特征使用SVM來進行分類。由于TI_CNN融合了兩種不同類型CNN輸出的特征，所以相比于傳統1-D CNN、2-D CNN能獲得更多的特征。TI_CNN相比于CNN+LSTN[21]，具有更淺的網絡層次。所以在輸入數據量小的時候不容易出現過擬合的現象，并且識別時間更短。通過對比LeNet-5型1-D CNN與TI_CNN的性能差異證實：本文所提模型能更好的對振動信號進行分類，并且由于采用了SVM進行最后的識別分類，可以將全連接層的數量減小且識別時間也滿足了實時識別的要求。

1 使用TI_CNN分類的方法

在對路面振動事件的長距離監測中,所使用的分布式光纖聲傳感器系統，如圖1所示。所采用的分布式光纖聲傳感器系統主要分為3大部分：φ-OTDR傳感系統、傳感光纖、信號識別單元。分布式光纖聲傳感系統的主要工作步驟如下：

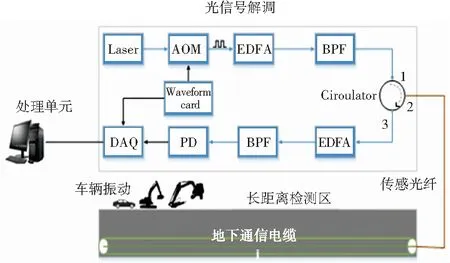
圖1 phi-OTDR 系統實驗設置

(1)激光經過聲光調制器(AOM)后被調制為光脈沖。該光脈沖被摻鉺光纖放大器(EDFA)放大后通過一個帶通濾波器(BPF)，濾除由EDFA產生的放大自發輻射(ASE)噪聲。

(2)得到的濾波光脈沖從環形器的1號端口進入環形器，再從環形器的2號端口射入傳感光纖。由傳感光纖返回的后向瑞利散射光經環形器的3號端口輸出到EDFA，經過EDFA放大后，再使用BPF濾除ASE噪聲。

(3)光電探測器將濾波后的后向瑞利散射光轉換為電信號，在通過信號采集卡后將采集到的信號輸入到信號處理單元進行識別。

在本次應用中，主要的識別任務是區分通過路面的汽車、路面挖掘機的挖掘工作和路面破路機的工作事件。

圖中，AOM為聲光調制器;EDFA為摻鉺光纖放大器;PD為光電探測器;DAQ為數據采樣器。

本文所提出的TI_CNN的識別方式如圖2所示，主要步驟為：數據的預處理、數據集的準備、數據集轉為小波時頻圖、使用TI_CNN進行訓練、對訓練結果分類。

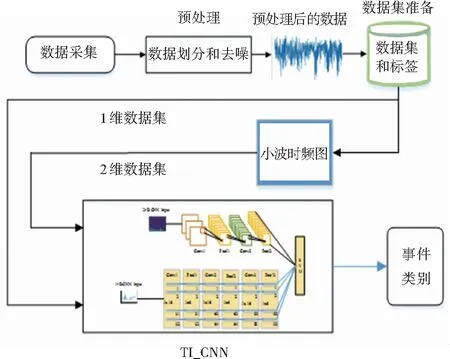
圖2 系統操作過程

1.1 數據去噪

振動數據是通過采集傳感光纖上每個點的空間響應以及積累沿時間軸的空間響應得到的。獲得的在每個點空間的一維時間序列被輪流作為識別目標。由于在實際環境中存在有許多的噪聲，導致信號被淹沒在各種噪聲中，嚴重影響最后的識別結果。因此，在對數據進行分析之前，需對數據進行去噪處理。本文使用文獻[22]中提到的基于小波分解的信噪分離方式，并使其更好的應用到分布式光纖振動傳感信號上。WD的處理過程如圖3所示。

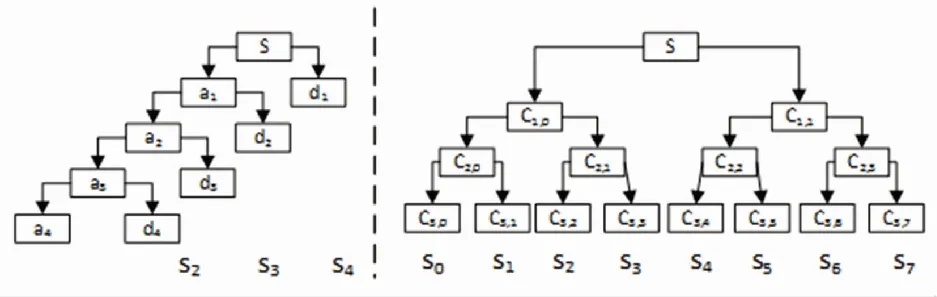
(a)WD方法 (b)WPD方法

小波包分解與小波分解相比，小波包分解能將前一步分解結果中的高頻部分繼續分解，會將原始信號分解到2i(i為分解尺度)小波包子空間中。因此，小波包分解能得到比小波分解更詳細的信息。小波包分解公式為：

(1)

(2)

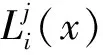
小波包重構的公式為：

(3)

因此，在本文中使用一個3層，母波為‘sym8’的小波包分解，對振動信號進行去噪。小波包分解的層數和母波類型是通過實驗選擇的最優設置。

1.2 數據集準備

在圖1所示的對地面振動事件的監測中存在著很多的振動源，而本文主要研究小汽車通過，挖掘機挖掘，破路機工作這3種振動源，將這3種事件依次命名為類型1、類型2、類型3。

1.3 數據集轉為小波時頻圖

對時序信號的分析主要有兩種方式：連續小波變換(CWT)、短時傅里葉變換(STFT)。STFT的窗口是固定的，在實際使用中很難尋找到一個合適的窗口大小。一方面，如果窗口尺寸太窄，則窗口所截取的信號將太短，從而導致頻率分析不精準。另一方面，如果窗口尺寸太寬，則導致截取的信號長度太長，從而導致較低的時間分辨率。所以短時傅里葉變換不能滿足非穩態信號變化的頻率要求.

連續小波變換很好的解決了短時傅里葉變換(STFT)固定窗口的問題。其通過采用一個有限長衰減小波基函數來代替STFT中的無限長三角基函數，更適合用于非穩態的時序信號的處理。通過使用CWT，可以將一維時序信號轉變為二維的時頻圖像。二維時頻圖像包含了一維時序信號的時間和頻率的信息，相比于原始信號，時頻圖能全面、更準確的反應出原始信號的特征。

分布式光纖傳感系統返回的振動信號屬于非穩態信號，所以采用CWT對其進行分析。對任意L2(r)空間的函數f(t)，其CWT的變換方程如下：

(4)

其中：

(5)

在公式(4)中，a是一個尺度分解因子，a> 0代表頻率相關拓展；b是平移量，代表時間相關的拓展；ψa,b(t)是小波基函數。

給出尺度分解因子和小波基函數后，就可以根據公式(1)得到各振動信號的小波系數，并將小波系數序列轉變為實際的頻率序列。結合點序列，畫出各振動信號的小波時頻圖。

對分布式光纖聲傳感系統采集的振動信號進行小波時頻分析中，根據實驗得出最優小波基函數參數選擇‘Cgau1’，尺度分解因子為30。小汽車通過、破路機工作、挖掘機挖掘所生成的小波時頻圖像如圖4所示。

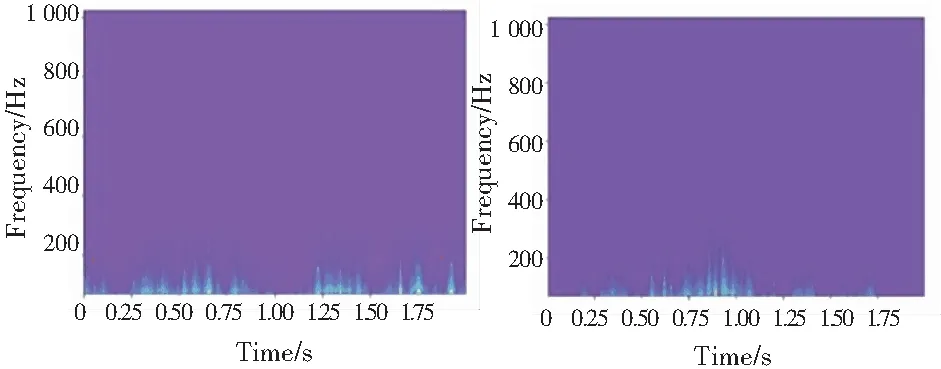
(a)汽車通過的情況 (b)挖掘機工作的情況

1.4 基于TI_CNN訓練

采用TI_CNN(3層1-D CNN、2層2-D CNN)比采用單獨網絡結構的LSTM、1-D CNN、2-D CNN得到更好的性能，如圖5所示。

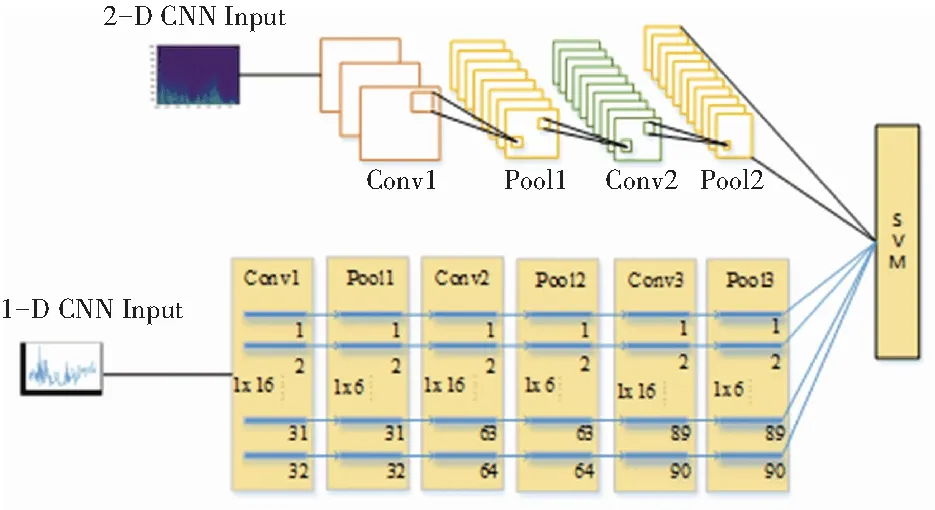
圖5 TI_CNN網絡

圖5顯示出該識別網絡具有兩種不同輸入類型卷積神經網絡。下臂使用的神經網絡結構為3層1-D CNN，其網絡結構參數見表1；由于2-D CNN輸入的參數較多運算量較大，所以在本文中提出僅采用2層2-D CNN對小波時頻圖進行識別，大大減小了2-D CNN對圖像特征提取的時間，雙層2-D CNN的網絡結構參數見表2；使用兩個全連接層(FC)將上下臂卷積神經網絡輸出的特征映射到樣本標記空間，從而將所有特征整合到一起，最后使用一個SOFTMAX分類層輸出各標記事件的概率值。其網絡結構參數見表3。

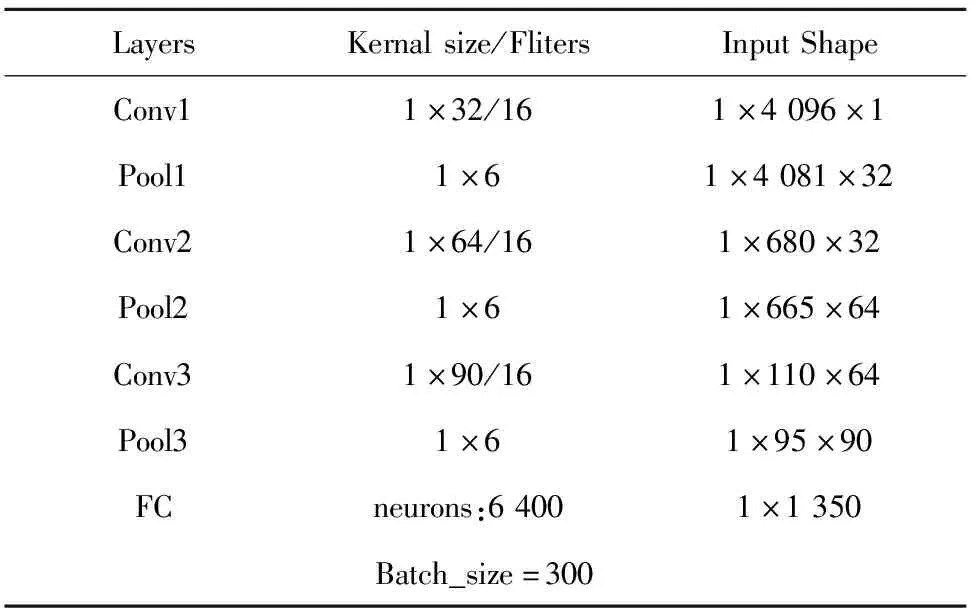
表1 1-D CNN的參數

表2 2-D CNN 的參數

表3 全連接層的參數

使用TI_CNN進行分類前需要先將CNN模型訓練好，但由于SVM不能進行反向梯度傳播，故先使用softmax層來輸出TI_CNN的準確率，當準確率達到要求時便認為TI_CNN的模型已經訓練好，再將訓練好的TI_CNN模型用來提取特征，使用SVM來進行最后的分類。SVM的核函數設置為高斯核函數，超參數C設置為0.09，degree設置為3。

下臂的1-D CNN網絡輸入的是經過濾波的原始一維振動信號，上臂的2-D CNN網絡輸入的是使用濾波信號經過CWT得到的小波時頻圖。卷積層和全連接層使用的激活函數都是線性整流函數(ReLU)。ReLU是一個非線性函數，其定義如下：

φ(x)=Max(x,0)

(6)

ReLU激活函數可以有效避免梯度消失的問題，并且運算簡單，可以提高計算速度且能讓網絡很快收斂。

TI_CNN采用的損失函數為：

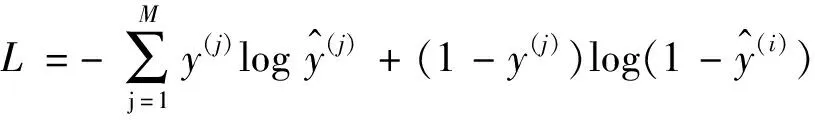
(7)

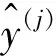
采用隨機梯度下降(SGD)去更新TI_CNN的網絡參數。在本文中SGD損失函數的學習率設置為0.01，該參數是經過實驗得出的最優參數。在訓練結束后，使用Accuracy、Recall、Precision、F1來評估模型的有效性。具體公式如下：

(8)

(9)

(10)

(11)

式中，TP代表在判斷正類中判斷正確的個數；TN代表在判斷負類中判斷正確的個數；FP代表在判斷正類中判斷錯誤的個數；FN代表在判斷負類中判斷錯誤的個數。

2 實驗

實驗設置如圖1所示。一個線寬為3 kHz,能源為10 mW的分布式反饋激光器(DFB-LD)產生連續激光。這個光源被AOM(100 M)調制為光脈沖。然后通過一個EDFA(插入損耗為4 dB,增益為27 dB)被放大，并使用BPF濾除ASE噪聲。這個光被注入一段20 km長的傳感光纖中通過一個光學環形器。后向瑞利散射光往回傳播通過傳感光纖，由EDFA放大和BPF濾波后被PD(100 M)檢測，然后由采樣率為200 MS/s，位數為12 bit的DAQ采樣。實驗數據在上海滬松路和文翔東路工地上采集。其中，20 km長的傳感光纖被深埋在地下大約1～2 m處。

實驗中，3種主要的振動事件被選擇作為振動信號識別的對象，總共設置1 200個一維數據樣本和1 200個小波時頻圖樣本，按照7：3的劃分比例，隨機將數據劃分為訓練集和測試集，每個樣本的幀長為2 s。在施工現場的左方大約5 m處有一條大約4.8m寬的公路，當有汽車通過時便記錄下此時的振動波形；挖掘機挖掘是挖掘機在施工現場進行挖掘工作時采集到的波形；破路機工作是指將挖掘機原有的鏟斗更換為破碎錘時進行工作的振動信號。振動識別實驗在一臺配備了NVIDIA Quadro P5000 GPU的圖形工作站上進行。

本文中，CNN結構是在基于keras框架上使用python編程語言實現的。LeNet-5 1-D CNN結構如圖6所示。

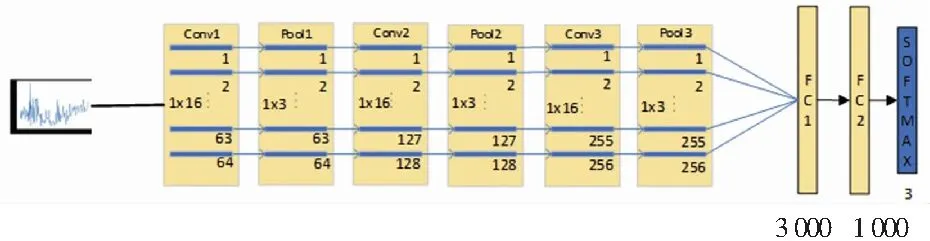
圖6 1_D CNN 結構

網絡詳細信息見表4。表4中主要展示了1-D CNN網絡的輸入值大小、卷積層中卷積核的大小以及卷積核的數量。

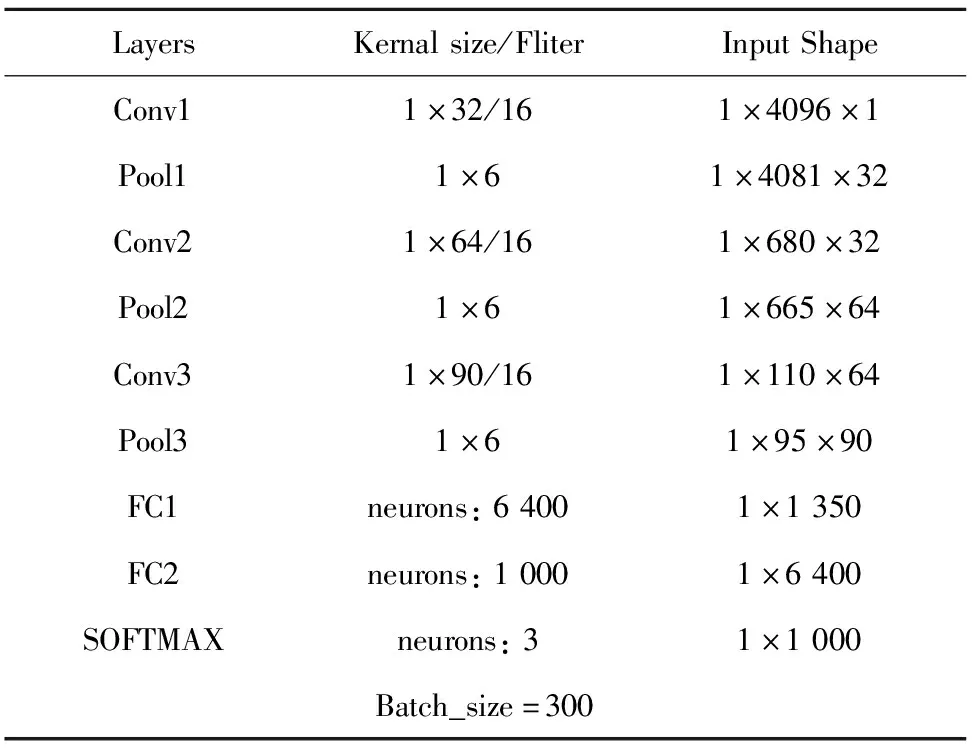
表4 LeNet-5 1D_CNN 參數

上述兩個網絡每次迭代輸入的數據量(Batch_size)設置為300。LeNet-5型1-D CNN網絡輸入的是數據集中的經過濾波后的一維原始信號樣本。TI_CNN(輸入的是經過濾波的一維原始信號和使用濾波后的一維信號通過CWT得到的小波時頻圖。

兩種方法在測試集上的混淆矩陣如圖7所示。在圖7中，使用TI_CNN對小汽車通過、挖掘機挖掘、破路機工作的識別準確率分別為95%、94%、100%，平均識別率為96.3%；LeNet-5 型1-D CNN對小汽車通過、挖掘機挖掘、破路機工作的識別率分別為94%、93%、86%，平均識別為91%。

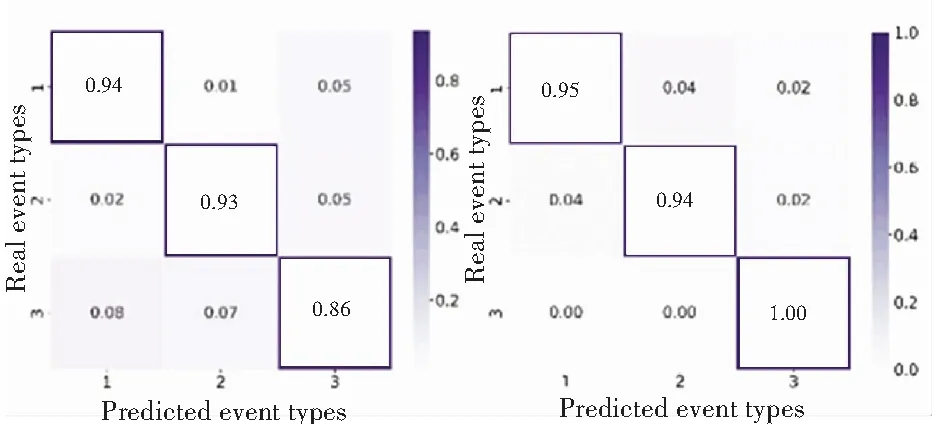
(a)1_D CNN(LeNet-5)方法 (b)TI_CNN方法

由此可見，由于TI_CNN采用兩種卷積神經網絡對振動信號進行特征的提取，能提取到更加豐富的特征，再加上使用SVM進行分類，使其準確率和識別時間都有所提升，其平均準確率高于LeNet-5型1-D CNN。TI_CNN和LeNet-5型1-D CNN的驗證集損失函數下降曲線如圖8所示、驗證集準確率上升曲線如圖9所示。

在圖8中，LeNet-5型1-D CNN損失函數的下降速度優于TI_CNN，但在圖9中，LeNet-5 1-D CNN出現過擬合(準確率曲線振蕩過大)的程度比TI_CNN嚴重。其主要原因是：TI_CNN不僅從原始一維信號中提取出信號的時域特征，還從小波時頻圖中獲得了時頻域特征，而LeNet-5 1-D CNN只能從一維信號中獲得信號的時域特征。TI_CNN由于合并了兩種卷積神經網絡的特征,加大了識別的數據量，所以在輸入數據量較小時也不易出現過擬合。

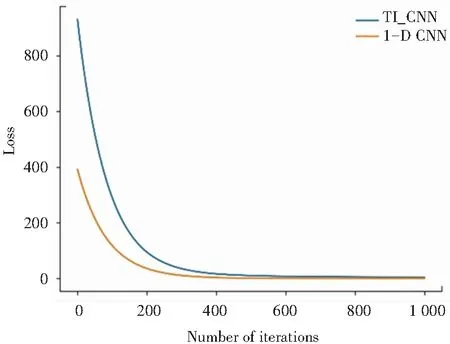
圖8 損失函數下降曲線

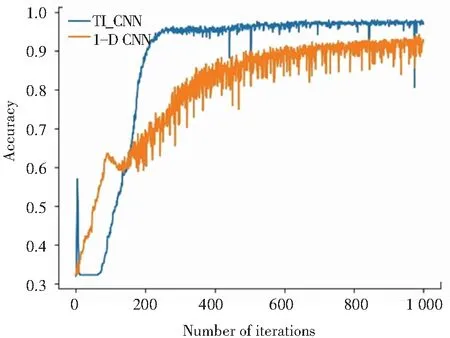
圖9 準確率上升曲線

表5為LeNet-5型1-D CNN和TI_CNN識別結果計算指標的對比。從表中可以看出：TI_CNN的各項計算指標都優于LeNet-5型1-D CNN，這說明TI_CNN模型能很好的識別各種振動數據。

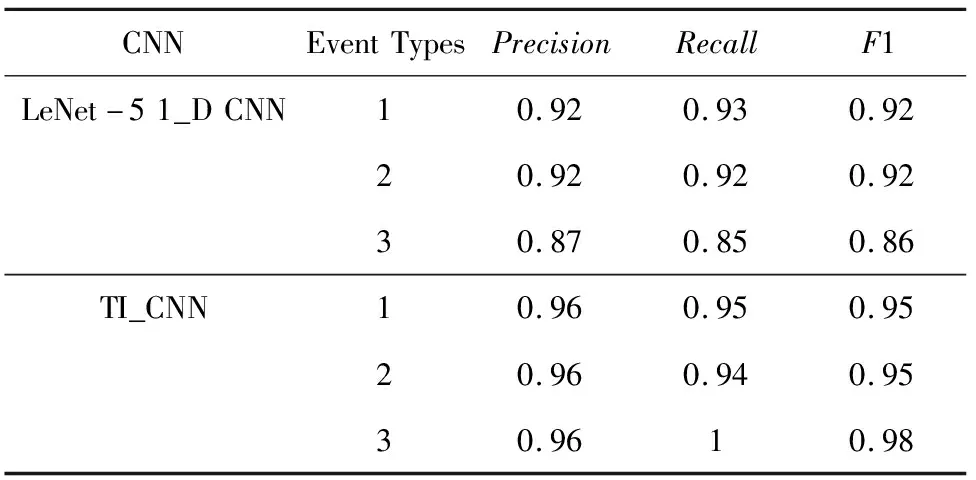
表5 TI_CNN 和 LeNet-5 1_D CNN識別結果對比

3 結束語

本文提出了一種新穎的方式，去識別分布式光纖聲傳感器采集的振動事件，提高了檢測精度。為了驗證所提方法的有效性，將該方法與文獻[19]中所提出的多層1-D CNN識別模型進行了對比，實驗證明TI_CNN可以在使用較小數據集時，達到較好的效果并且降低過擬合現象的出現。該方法通過同時提取一維信號的時域特征和小波時頻圖的時頻域特征增加了最后識別的特征數量，但網絡層次并沒有加深，減小了模型的過擬合和識別時間，提高了識別的準確率。

基于本研究采集的數據構成的數據集，采用TI_CNN對小汽車通過、挖掘機挖掘、破路機工作的識別準確率分別可以達到95%、94%、100%，平均識別率為96.3%，并且識別時間為0.61 s.