機場值機柜臺資源的配置研究

顏建影，石麗娜

(上海工程技術大學 航空運輸學院，上海 201620)

0 引 言

隨著中國經濟持續穩定的增長，對基礎設施的投資越來越大，使得人們的出行越發方便，越來越多的普通百姓把飛機作為一種交通方式的選擇，但隨著乘坐飛機旅客的持續增多，使得機場的運行配置資源越發緊張，運行管理變的越發重要。當前，國內開始不斷增建新機場或擴建機場，這種方式雖可以解決燃眉之急，但要想根本的解決機場運行資源緊張的局面，還要更加合理的使用運行資源，并且隨著智能化、高效機場建設，對值機柜臺資源的動態配置，提高服務效率變得更加重要。機場航站樓中運行最為復雜的流程為值機流程，因此對于提高旅客滿意度，實現資源的高效利用具有重要作用[1]。因此，確定所需值機柜臺配置數量是機場和航空公司對于旅客到達機場航站樓所需解決的首要問題。

此前，關于值機柜臺資源分配問題，相關人員也進行了多方面的研究。文獻[2]提出把值機柜臺的分配問題轉換成多維放置問題，即在空間有限的情況下，盡可能多的放置值機柜臺。但其中并沒考慮高峰期旅客排隊等候值機，在機場值機區域有限的情況下，每多放置一個柜臺旅客排隊等候值機的區域則會相應減少，使得原本就擁擠的值機區域越發擁擠，反而使旅客滿意度降低。文獻[3]通過調查機場旅客到達時刻以及航班離港時間數據，建立值機柜臺的指派優化模型，該模型采用計算機仿真軟件運行模擬，并未涉及具體算法。文獻[4]提出了協助機場分配公用值機柜臺的整數規劃模型，但該模型考慮的參數過多，求解過于復雜，實際應用困難。文獻[5]建立了在達到旅客滿意度的條件下，使人工成本最小的模型。該模型將值機和安檢都考慮在內，并不是單純對值機成本的求解，且對旅客的到達過程假設為單純的指數分布，而實際中值機旅客的到達曲線往往為上下浮動的曲線。同時，隨著自動值機設備的發展，使用自助值機設備進行值機的旅客也逐年增多。文獻[6]中以同時考慮租用柜臺成本和顧客時間成本為前提，將自助值機柜臺轉化為人工值機柜臺進行分析，但在旅客值機的選擇時只是單純的將有行李的旅客分為人工值機，而無行李的旅客選擇自助值機。文獻[7]為求算最佳的值機柜臺排班策略，運用派邇值機柜臺規劃實驗系統，將人工值機柜臺和自助值機柜臺分開進行分析，求解最小的人工值機柜臺成本。通過計算機對值機流程進行仿真分析，沒有涉及到具體的算法且值機柜臺開放數量始終為一定值，而現實中各個時段開放的值機數都是變化的。文獻[8]將人工值機柜臺和自助值機柜臺資源共同分析研究，以所有旅客行走距離之和最短為優化目標，實現對自助值機柜臺和人工值機柜臺的合理分配，但文中并未考慮旅客的到達分布以及值機排隊等待時間。

當前機場值機柜臺的分配，越來越重視自助值機設備的使用。因此，本文在求解值機系統所得凈收益最大時，首先將滿足一定條件的旅客滿意度約束考慮進去，然后在分析人工值機柜臺時，將自助值機設備的使用情況也進行了分析，最后將自助值機設備使用產生的收益考慮進去。通過實例分析，最終得到相應的動態值機柜臺分配數量，為機場航站樓值機系統柜臺的資源配置提供一定的參考。

1 機場值機流程的分析

旅客值機是機場離港流程中的一部分，分為人工值機和自助值機兩種方式。旅客到達機場航站樓值機大廳，根據個人喜好選擇人工值機或自助值機子系統，同時根據各系統的排隊情況，選擇最短的隊列等候值機。

1.1 值機流程排隊系統

值機流程作為航站樓旅客流程的子系統，其運行效率的高低，決定了旅客其它步驟的運行。其中，旅客到達的過程與航班時刻表、航班旅客人數以及旅客到達分布曲線有關。某一時刻t的旅客到達率γ(人/min)為各航班該時刻旅客到達率之和，如公式(1)。

(1)

式中，l表示t時刻內航班的個數，a={1,2,…,l}。

值機過程服從M/M/k的排隊模型排隊系統[9]，有k個服務臺，各服務臺服務率等于u(人/min)，總服務率為ku。因此，值機柜臺的服務強度為值機系統總到達率與總服務率之比，值機柜臺服務強度ρ應小于1。

(2)

(3)

(4)

其中，式(2)為服務強度計算公式；式(3)為旅客值機排隊平均旅客數；式(4)為值機排隊旅客平均排隊時間(min/人)；k為開放的值機柜臺個數。

1.2 基于服務標準的值機柜臺資源配置

目前，機場一般要求航站樓的值機服務必須滿足一定指標。見表1所列：中國民用航空局發布的民用運輸機場服務質量標準[10]。因此，本文在求解值機柜臺開放數量時，應以滿足機場值機排隊等待時間標準為前提。即：

Wt≤Wc

(5)

式中，Wc為某服務水平下，標準值機排隊等待時間。

2 值機柜臺分配模型的建立

2.1 假設條件

根據以上對值機流程的分析，為便于計算，對值機過程進行以下假設：

(1)機場到達旅客全部使用值機柜臺進行值機，即人工值機柜臺和一體化自助值機設備。

(2)值機過程滿足先到先服務的原則。

(3)值機排隊系統的各時段所需柜臺數為正整數。

(4)值機方式為公用柜臺，旅客到達時選擇最短隊列排隊。

(5)旅客全為經濟艙旅客。

(6)人工值機柜臺配置服務人員，自助值機設備不配置服務人員。

2.2 不同時間段值機方式的選擇

由于旅客選擇值機方式具有很大的隨機性，旅客選擇偏好，受旅客個人特征、值機設備特征等影響[11]。根據文獻[12]，得到某一機場早高峰時段值機排隊系統。旅客對于人工值機柜臺和自助值機柜臺的預測選擇偏好[12]，其選擇比例見表2。

表2 旅客不同值機方式選擇比例

由表2可知，在值機的早高峰時段，人工值機方式仍占據主導作用，但自助值機的占比相比平峰時段在高峰時段明顯增大。說明高峰時段，由于旅客人數增多，值機排隊時間變長，選擇自助值機的旅客增多。因此，為了對機場繁忙時段值機柜臺分配進行分析，本文選擇早高峰時段的旅客到達進行問題分析。

2.3 值機柜臺分配模型的建立

2.3.1 模型中符號含義

t：值機時間按照一定時間間隔，平分為n個時間段，t≥1,t={1,2,…,n}；

Xt：時間段t內，使用人工值機柜臺旅客所占比例，0≤Xt≤1；

Yt：時間段t內，使用自助值機柜臺旅客所占比例，0≤Yt≤1；

PU：人工值機柜臺服務一位旅客產生的收益；

PV：自助值機柜臺服務一位旅客產生的收益；

PW：開放一個值機柜臺單位時間成本。

2.3.2 目標函數模型的確定

由上述分析可知，本文以滿足IATA(International Air Transport Association)C級旅客排隊等待時間為前提，以值機過程凈收益最大為目標函數，來優化航站樓的值機柜臺資源分配問題。即在得到值機系統最大凈收益的同時，求得其分配的值機柜臺數量，凈收益越大表明值機系統的收益越高。

(6)

(7)

Wt≤Wc

(8)

kt≤C

(9)

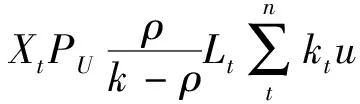
式(7)表示值機工作人員的繁忙概率，應控制在一個合理的范圍內。太大，服務員容易疲勞出錯，導致效率下降；太小，值機工作效率降低，柜臺使用率不高。另外，其取值范圍應該大一些，否則可能使問題解不可行，約束不滿足。

式(8)表示旅客值機排隊平均等待時間，應滿足服務標準。本文選取國內經濟艙95%的旅客值機排隊等待時間不超過14 min。

式(9)表示開放的值機柜臺數，該數值不可超過機場可開放最大值機柜臺數。其中C為可開放的最大值機柜臺個數。

3 值機柜臺動態分配參數設定

通過上述函數模型，選取某機場早高峰8：00-11：30值機區域的所有航班的實際旅客到達作為實例分析，可開放值機柜臺總數C為30。

3.1 旅客到達率的確定

本文選取30 min作為時間間隔，如果間隔時間太短容易造成值機排班難度大，造成人員排班混亂[13]。根據實際旅客到達人數，由公式(1)得到早高峰各時間段內的旅客到達率，見表3。

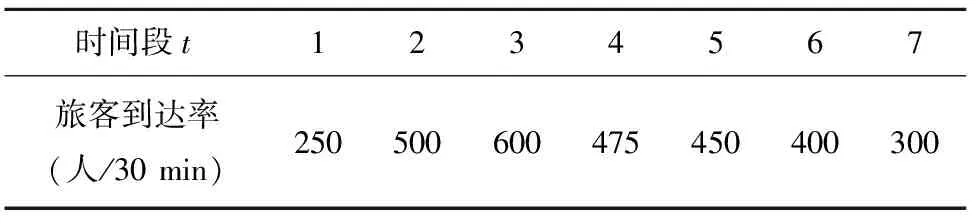
表3 各時間間隔旅客到達率

3.2 值機工作人員繁忙概率取值區間的確定

由于人工和自助的值機服務時間沒有顯著差異[12]，因此本文設定人工值機柜臺和自助值機柜臺旅客服務率相等，各柜臺的平均服務率u=23人/30 min。

首先，運用MATLAB對滿足約束條件的值機柜臺開放個數求解，得到各時段值機柜臺可開放數量(如圖1所示)，以及與之對應的值機人員繁忙概率(如圖2所示)。

圖1 各時間段值機柜臺可開放數量

圖2 值機柜臺可開放數量對應值機人員繁忙概率

由圖2可知，值機人員繁忙概率最大達到了8.127 2，導致值機工作人員極度疲勞，最小卻僅為0.002 5，值機柜臺工作效率極其低下，資源浪費。因此，應設定合理的取值范圍。同時為防止出現問題的不可行解，設定值機人員的繁忙概率取值為[0.25,0.91]。

4 值機柜臺動態配置的模擬退火算法設計

4.1 分配問題的模擬退火算法

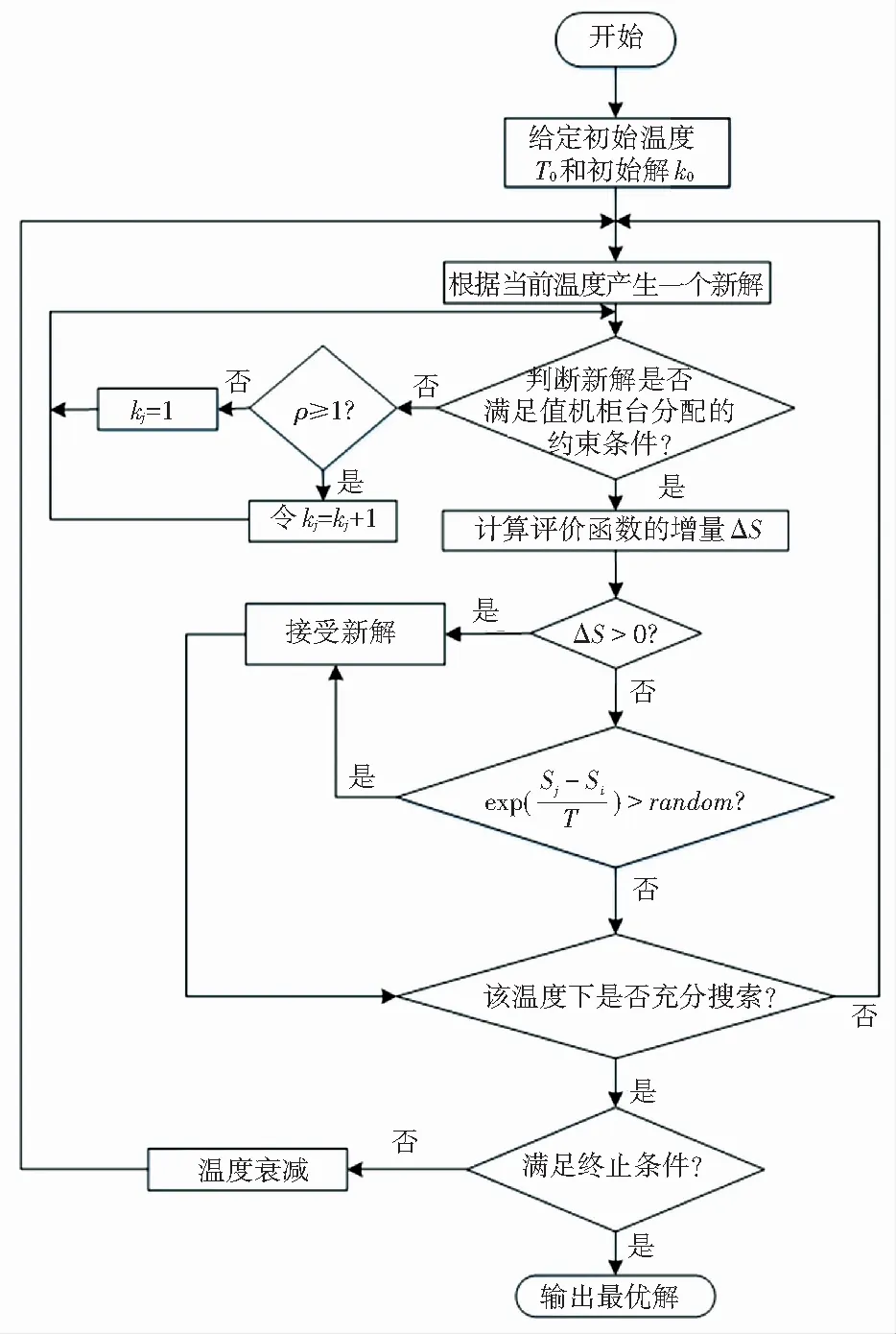
模擬退火算法最早由Metropolis等[14]在1953年提出。其原理與固體的退火原理類似，如圖3所示。即將固體溫度加熱后，再使其緩緩降溫冷卻，最后在常溫時達到穩定基態內能最小。當算法終止時，保存的最小解即為所求的最優目標函數值[15]。值機柜臺的分配問題，屬于NP難問題，若采用傳統方法，計算量和難度將會極大增加。因此，采用更加快速的方法來求解此類問題變得越發重要。1983年模擬退火算法第一次被引入優化領域，由于能有效的近似求解具有NP復雜性的難題，克服其它優化算法容易陷入局部最優的缺陷，并對初值沒有強依賴關系。基于此，將設計模擬退火算法用來求解值機柜臺動態分配問題。

圖3 關系原理

4.2 模擬退火算法實現

4.2.1 初始解的生成

為擴大求解范圍，本文初始解以隨機數的方式產生。在MATLAB中運用隨機數生成程序，隨機生成一個一行七列取值為[1,29]的矩陣。

4.2.2 目標函數的確定

本文值機柜臺分配問題的目標函數S，是在滿足約束的前提下，得到的最大值機凈收益。進而得到各時段分配的值機柜臺數量，如公式(10)所示：

(10)

本文目標函數求解為最大值，而模擬退火算法求解的是最小值。因此，在判斷是否接受新解時，改為當新解大于舊解目標函數時，則接受新解。

4.2.3 新解的產生

新解的產生應簡單快速，以減少算法所用時間。基于此，本文新解的生成通過交換的方式，以隨機概率的大小選擇以下兩種不同方式產生新解：

(1)二變換法

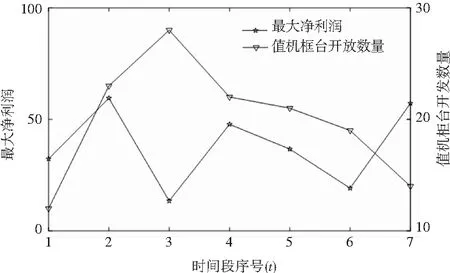
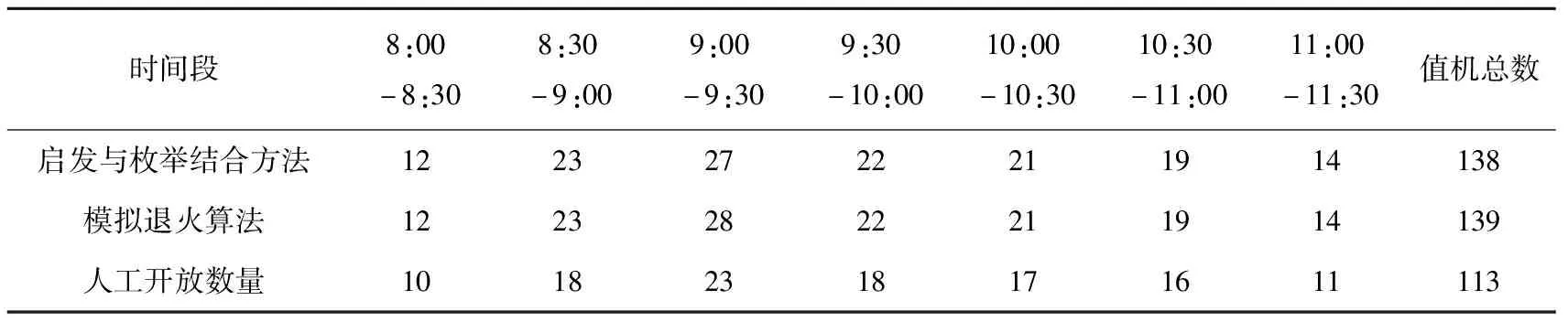
隨機選擇解中序號為u、v(設u

表4 二變換法

(2)三變換法

隨機選擇序號為u、v(設u

另外，由于目標函數本身帶有約束條件，當新解生成后，還要判斷是否滿足約束，如果滿足則進行算法下一步，否則根據新解服務強度的大小，進行相應改變。(具體過程在算法步驟Step3中介紹)

4.2.4 Metropoils新解接受準則

在模擬退火算法中，解的接受準則為Metropoils準則。因本文目標函數為求最大值，即新解的接受條件為：若ΔS>0，則接受新解kj作為新的當前解；如果ΔS<0，則新解kj按照接受概率P確定是否接受。如公式(11)、(12)所示。

ΔS=S(kj)-S(ki)

(11)

(12)

其中，ΔS為目標函數差;1≤i

4.3 運行參數

初始溫度T0：控制參數初始溫度T0=97。

衰減函數T：控制參數的衰減函數連續降溫表達式T=T×φ。φ是衰減函數的一個常數，取值為[0.50,0.99]之間，本文取0.90。

終止溫度Tf：終止溫度即算法運行的停止準則。一般終止溫度設為足夠小的正數，取值為[0.01,5]之間，本文取3。

Markov鏈長度Lk：Lk即循環次數，應能在控制參數T的取值上達到平衡。取值一般為100 n，本文設Lk為700次。

4.4 模擬退火算法步驟

根據前文設計，算法步驟如下：

Step1令初始溫度T=T0，并按照上述所述方式生成一個初始解k0。

Step2令T等于冷卻進度表中的下一個值Ti。

Step3根據當前解ki進行擾動，即進行交換操作，從而產生新解kj。判斷新解是否滿足柜臺分配的約束條件，如果滿足進行下一步，否則根據新解的服務強度ρ。如果ρ≥1，則kj進行加1操作，如果ρ<1，則kj=1，直到找到一個滿足約束條件的值機柜臺開放數量，并計算新解相應的目標函數值S(xj)，進而得到ΔS。

Step5在溫度為Ti值下，重復進行Lk次擾動和接受循環，即循環步驟3和4，直到滿足要求。

Step6判斷T是否達到終止標準。滿足，則停止運算輸出最優目標函數解，算法結束；否則，轉到步驟2繼續執行。

算法流程如圖4所示。

圖4 模擬退火算法流程

5 實例分析

設PU=10元/人、PV=5元/人、Pw=4元/min，通過MATLAB運用所設計的模擬退火算法求解目標函數，得到目標函數(值機系統)最大凈收益為265.92元。最優利潤為1.27元/min。最終得到各時間段最大凈收益和配置的值機柜臺數量(如圖5所示)，以及與之對應的值機人員繁忙概率大小(如圖6所示)。

圖5 各時段最大凈收益與值機柜臺開放數量

圖6 各時間段值機人員最終繁忙概率

將本文采用模擬退火得到的值機柜臺分配數量，與以往采用啟發式和枚舉式相結合的方法對人工值機柜臺進行分配的結果進行對比，值機開放總數基本相同。說明了算法的有效性，但啟發與枚舉結合的方法，往往需要運算經驗，并且人工運算需要大量時間，且相比本文所用算法，難以在機場實際應用。同時本文計算在考慮使用自助值機設備的情況下，人工值機柜臺開放總數量為113個，相比以往只對人工值機分配數量，本文人工值機柜臺減少了18.7%的使用量，提高了值機系統資源的利用效率。同時，分配更加合理，為機場提供了不同的值機柜臺資源分配方案，見表5。

表5 不同時間段值機設備動態開放數量

6 結束語

本文為機場航站樓內值機柜臺資源的配置研究，在滿足旅客滿意度約束標準的前提下，考慮值機員的繁忙程度，以系統凈收益最大為目標，通過設計的模擬退火算法，對值機柜臺資源進行動態配置求解。運用MATLAB進行實例分析，在P4，i5,1.19 GHz算法平均運行11 s，得到最大的系統凈收益，進而得到各時間段內值機柜臺的分配數量。結果表明，相比只考慮對人工值機柜臺的配置及采用啟發式運算的方法，本文在考慮了自助值機柜臺分配方式下，各時間段使用的值機柜臺數量分配更加合理，同時運算所用時間大大減少，提高了值機系統運行效率和旅客滿意度，為機場值機柜臺的運行配置提供了可行參考。