滯塵影響下的茶樹葉片水分高光譜估算

江 景，趙紫薇，蔡 唱，張勁松, 程志慶*

1.安徽農業大學資源與環境學院，安徽 合肥 230036 2.農業部合肥農業環境科學觀測實驗站，安徽 合肥 230036 3.中國林業科學研究院林業研究所，北京 100091

引 言

茶樹葉片水分是茶樹生長狀態以及茶葉品質的良好指示器。精確、快速、無損監測茶樹葉片含水量對茶樹生產精準管理具有重要指導意義。高光譜遙感可以無損、快速地捕獲地物微弱光譜信息，具有精準定量反演地物特征的巨大潛力，為植被葉片水分的精確、快速、無損監測提供了一種新的技術[1]。目前，已有較多學者在農作物和樹木上開展了基于高光譜信息的葉片水分估算研究，也取得了一定的成果[2-3]，但茶樹葉片水分光譜估算研究較少。且已有研究結果顯示在不同環境條件下，雖然針對同種植物使用同一方法，但獲得的葉片水分估算精度也具有差異，如: 胡珍珠等[4]利用水分指數(WI)對核桃葉片水分含量進行估算取得了較高精度，而潘慶梅等[5]利用該植被指數進行核桃葉片水分估算應用時，其模型估算精度不理想；其他水分植被指數光譜估算模型同樣存在精度差異顯著的現象[6-7]。針對以上現象分析發現，已有葉片水分光譜估算研究中均未涉及葉面滯塵對光譜信息的影響，而葉面滯塵的存在以及不同滯塵量對葉片光譜信息具有很大影響[8-9]，是影響葉片水分光譜估算應用魯棒性的問題之一。因此，分析葉面滯塵對高光譜信息估算植物葉片水分的影響，對茶樹葉片水分光譜估算精度的提高具有重要意義。

目前，葉面滯塵的高光譜研究主要集中于利用高光譜技術進行不同植被類型滯塵能力的比較、不同環境下不同植被類型滯塵能力的比較與分析、植被葉片特征對滯塵能力的影響、葉面滯塵率模型建立及估算研究[10-11]。而滯塵影響葉片水分高光譜模型估算精度以及如何降低滯塵對葉片水分高光譜估算的影響有待研究。茶樹由于其生長環境的差異性，造成了不同的葉面滯塵環境。因此，以茶樹為研究對象，討論并分析茶樹葉片水分在滯塵影響下的光譜變化規律、通過相關系數法構建新指數，對比分析不同滯塵狀態對新建指數、已有水分指數與葉片含水量相關性的影響，篩選受滯塵影響小且與葉片含水量相關性高的植被指數，用以降低滯塵的干擾，提高茶樹葉片水分估算精度，以期為茶樹葉片水分在復雜環境下的精準估算提供重要的理論基礎，為減少葉面滯塵影響高光譜信息的應用提供技術支撐。

1 實驗部分

1.1 樣品采集

試驗地位于安徽農業大學農萃園茶葉園(117°14′49.44″E，31°52′2.66″N)，茶樹品種為“舒茶早”。采樣時間為2019年4月5日—10日，采用隨機采樣方式，采集無損、健康的茶樹鮮葉，葉片樣本共350個。采樣過程中避免抖動；樣本采集后立即放入已編號的保鮮袋、封口后立即帶回實驗室進行數據測定。

1.2 數據測定

1.2.1 光譜反射率測定

用美國ASD公司生產的Field Spec Pro光譜儀(光譜波段范圍為：350～2 500 nm，視場角25°)自帶的植被探頭與葉片夾式光譜探測器在室內分別對茶樹葉片樣品進行滯塵清除前和清除后的光譜測定，并將滯塵清除前后數據分別標記為有塵(dl)、無塵(cl)，測量中被測葉片面積保持相同且葉面平整，以有效消除背景反射、葉片表面彎曲而造成的光譜波動，保證結果的精確性。同時為減少測量誤差，測量前利用標準白板校正。每個樣本采集光譜數據3次，并取其平均值作為該樣本光譜反射率。共獲取350組茶樹葉片光譜數據。

1.2.2 單位滯塵率、葉片含水量測定

采用萬分之一電子分析天平分別測定滯塵清除前葉片質量和滯塵清除后葉片質量，然后利用掃描儀對該葉片進行掃描并計算葉面積(為了防止水分的變化上述步驟均在10 min內完成)。利用式(1)計算單位滯塵率(UDR)

(1)

式(1)中，UDR為葉片單位滯塵率，g·cm-2；M1為滯塵清除前葉片質量，g；M2為滯塵清除后葉片質量，g；S為葉面積，cm2。

單位滯塵含量測定后，將該葉片放入烘箱105 ℃殺青15 min，90 ℃持續烘干至葉片質量不再變化，稱取烘干葉片質量。利用式(2)計算葉片等效水厚度(EWT)

(2)

式(2)中，EWT為葉片等效水厚度，g·cm-2；M2為滯塵清除后葉片質量，g；M3為葉片烘干質量，g；S為葉面積，cm2。

1.3 數據分析

1.3.1 數據概況

為了保證數據的獨立性，提高模型的適用范圍及穩定性，將350組數據隨機分為特征波段提取集、建模集、檢驗集，每個集合內均包含了全滯塵率及含水量的茶樹葉片，如表1所示。利用View Spec Pro軟件對茶樹葉片光譜反射率進行平均與數據導出處理；通過MATLAB 2012b和SPSS 21.0進行相關系分析與建模，利用Origin 8.0進行繪圖。

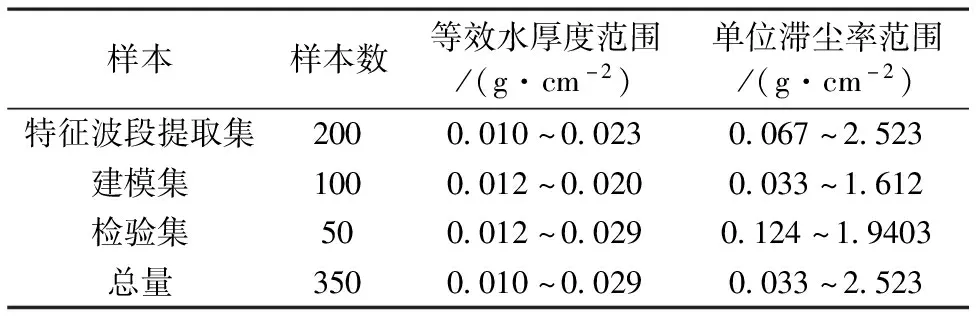
表1 樣本信息

1.3.2 植被指數

植被指數(VI)是兩個或多個波長范圍內的地物反射率組合運算，能有效地增強植被某一細節，通過植被指數來區分各種植被的方法運算簡單，便于操作，實用性強。雖然目前有較多植物水分植被指數，但這些指數構建時并未考慮到葉面滯塵的因素。因此，本研究利用特征波段提取集的200組數據通過隨機組合葉片有塵原始光譜350～2 500 nm的任意兩波段，利用常見的歸一化計算法、比值計算法構建植被指數并分別與EWT進相關性分析[12]，提取最佳組合波段，最終分別構建新歸一化植被指數(NDVI)和新比值植被指數(RVI)。

歸一化計算法公式如式(3)所示

(3)

式(3)中，NDVI(i，j)為以i和j為中心波段歸一化植被指數；Ri和Rj分別為i和j波段的光譜反射率。

比值計算法公式如式(4)所示

(4)

式(4)中，RVI(i，j)為以i和j為中心波段的比值植被指數；Ri和Rj分別為i和j波段的光譜反射率。

為分析植被指數在不同滯塵條件下對茶樹葉片高光譜估算的響應，同時選取6種常用精度較高的水分指數，其新建植被指數與常用水分指數如表2所示。

表2 植被指數及計算方式

1.3.3 分析方法

不同植被指數對滯塵影響的響應大小以相對變率(RCR)作為評判指標，若RCR越大表明該植被指數受滯塵影響越大，若RCR越小則反之。RCR的計算公式如式(5)所示

(5)

式(5)中，RCR為相對變率；xn為無塵狀態下的相關系數；xy為有塵狀態下的相關系數。

1.3.4 模型構建與驗證

偏最小二乘回歸(PLSR)是一種結合了多元線性回歸分析、典型相關分析和主成分分析三種算法優點的化學計量分析方法，廣泛應用于光譜分析[13]。因此，采用PLSR構建水分估算模型，并利用均方根誤差(RMSE)、決定系數(R2)、剩余估計偏差(RPD)對不同植被指數構建模型的預測能力和穩定性進行評價，最終獲得葉面滯塵影響最小的高精度茶樹葉片水分指數估算模型。

2 結果與討論

2.1 滯塵對茶樹葉片光譜反射率的影響

為分析滯塵對茶樹葉片光譜反射率不同波段的影響，將光譜數據劃分為具有區分度的分組，根據滯塵率從小到大分為3組每組100個數據樣本，每個分組間均空除25個數據樣本，分組結果如下：0.033～0.31, 0.34～0.545和0.602～2.523 g·cm-2，并對每組的葉片有塵與對應無塵狀態下光譜數據分別進行平均處理，并對不同狀態下相同波段反射率進行差異性檢驗，具體結果見圖1。由圖1可見，大于400 nm波段的葉片光譜反射率曲線在除塵前、后呈現相似形態，且在680～780 nm間均出現了光譜反射率曲線的斜率發生驟變的植被典型“陡坡”現象，但小于400 nm波段光譜反射率變化較為復雜且無規律，可見該波段區間光譜反射率并不穩定，而相關研究指出葉片水分有效光譜信息幾乎不受小于400 nm波段的影響，因此，分析葉片水分光譜特征時可忽略小于400 nm波段區間的光譜信息。400～530，579～696和2 454～2 500 nm波段范圍內有塵葉片均明顯高于無塵狀態下相同葉片的反射率；其中400～530 nm波段范圍各滯塵狀態下不同葉片的反射率重疊非常明顯；579～696 nm波段范圍雖然無塵葉片反射率差異較為明顯，但有塵狀態下葉片反射率重疊較多；而2 454～2 500 nm波段范圍有塵無塵狀態葉片反射率聚類較為明顯，但同種滯塵狀態下的葉片反射率差異不顯著。531～578和711～1 378 nm波段范圍無塵葉片反射率大于該葉片有塵狀態光譜反射率，且滯塵率越小反射率越大；其中531～578 nm波段范圍無塵葉片反射率與有塵葉片反射率交叉現象嚴重；而711～1 378 nm波段范圍無塵葉片反射率與有塵狀態反射率具有明顯聚類現象，且相同狀態下的不同葉片反射率差異性極顯著(p<0.01)；1 379～1 882 nm波段范圍雖然無塵葉片光譜反射率均高于相同葉片有塵狀態反射率，但無塵狀態和有塵狀態下葉片反射率重疊明顯。可見，茶樹葉片光譜反射率受到滯塵影響其531～578和711～1 378 nm波段范圍受到滯塵影響光譜反射率具有顯著的降低趨勢，而400～530，579～696和2 454～2 500 nm波段范圍受到滯塵影響光譜反射率具有顯著的增加趨勢。711～1 378 nm對于不同滯塵率狀態具有明顯聚類現象，且差異性顯著。因此，711～1 378 nm區間在葉面滯塵對茶樹葉片水分估算影響研究中具有較大潛力，且本研究對所有波段進行兩波段組合并進行歸一化計算與比值計算，利用相關系數法篩選并新建的歸一化指數和比值指數的波段亦位于該潛力波段區間，分別為1 298，1 340和1 298，1 325 nm。

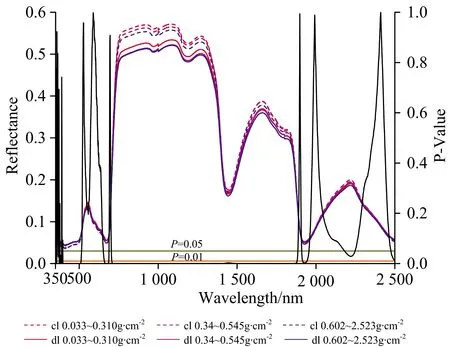
圖1 有塵和無塵茶樹葉片光譜反射率對比

2.2 滯塵對茶樹葉片含水量與植被指數相關性的影響

利用建模集的100組數據分別進行植被指數與茶樹葉片有塵、無塵狀態下的EWT相關性分析，并對相關系數進行相對變率計算，結果見表3。由表3可見，植被指數與EWT的相關系數在無塵狀態下均高于有塵，且絕對值皆已達到0.7以上；除MSI與EWT呈負相關外，其余7個指數與EWT均呈正相關；無塵狀態下NDVI(1 298，1 340)，RVI(1 298，1 325)與EWT相關性最高，分別達到0.865和0.864，而有塵狀態下NDVI(1 298，1 340)與EWT相關性最高，達0.848。對比無塵、有塵狀態下植被指數與EWT的相關性方向(即正、負相關性)可知，無論是否有塵植被指數與EWT的相關性方向不會改變，只會改變相關性的大小，且有塵狀態下各植被指數與EWT的相關性始終低于無塵狀態。對比植被指數與EWT相關系數的相對變率大小可知，NDVI(1 298，1 340)，RVI(1 298，1 325)，NDWI(860，1 450)和SIWSI的相對變率均小于0.06，其大小分別為0.019，0.023，0.051和0.060，可見以上4個植被指數受到葉面滯塵影響較小；且葉片有塵、無塵狀態下的EWT與以上4個植被指數相關系數均顯著(p<0.01)達到0.754以上。

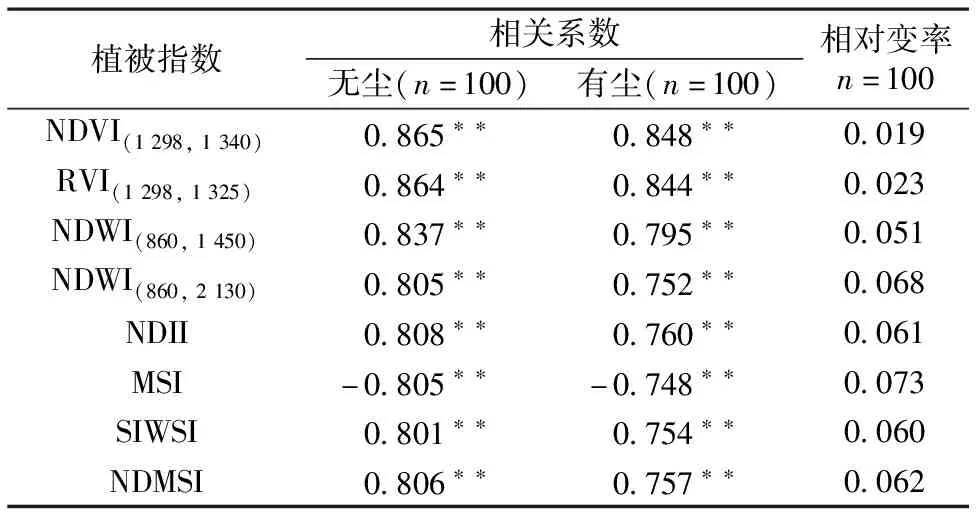
表3 茶樹葉片EWT在有塵、無塵狀態下分別與各指數的相關系數

2.3 滯塵對茶樹葉片水分估算精度的影響

根據上述結果可見NDVI(1 298，1 340)，RVI(1 298，1 325)，NDWI(860，1 450)和SIWSI受滯塵影響小，且與EWT的相關性最高。因此，利用這4個植被指數作為自變量，分別構建有塵、無塵狀態下茶樹葉片EWT估算模型用以分析葉面滯塵對各植被指數構建模型精度的影響。

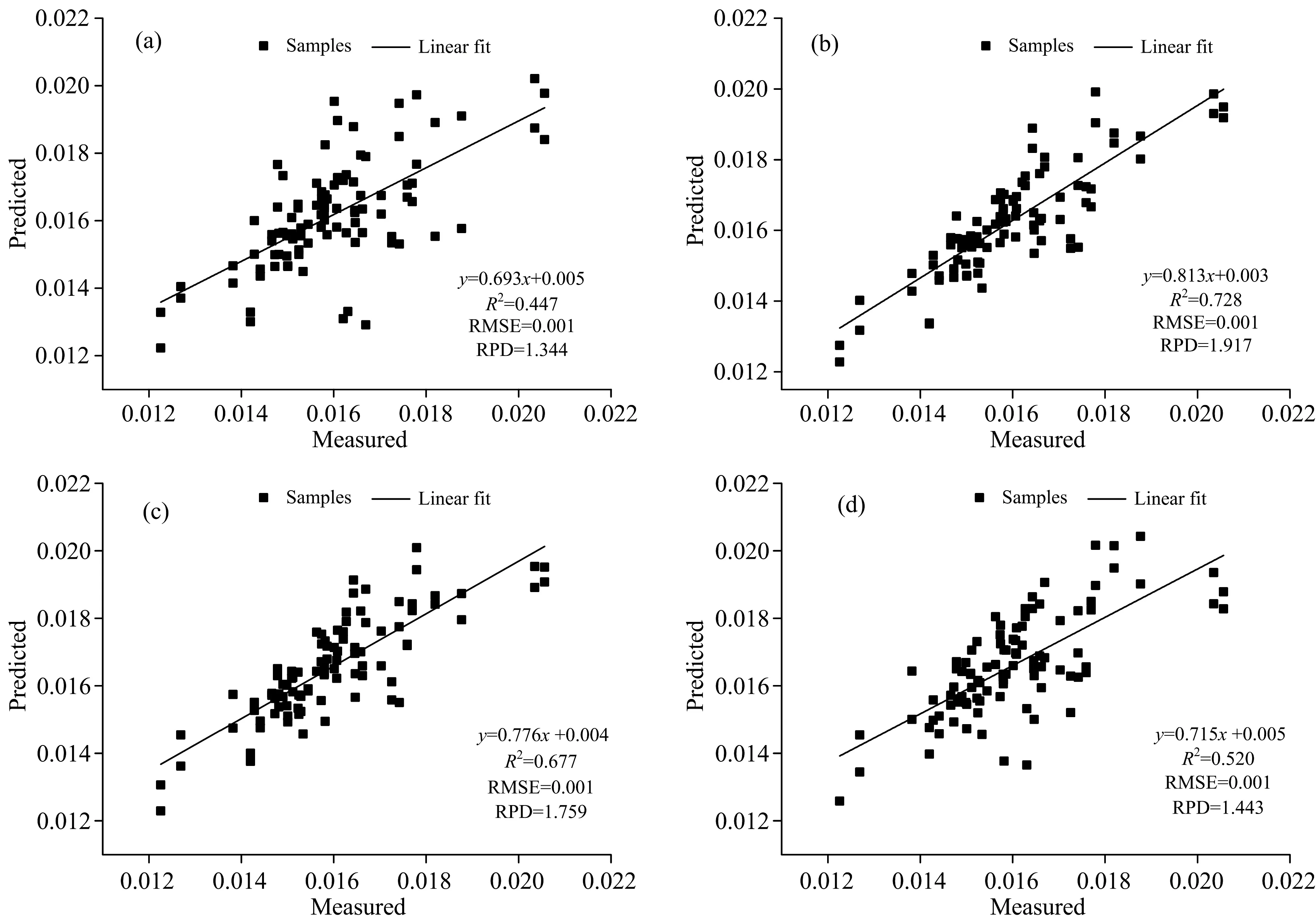
利用建模集數據的葉片有塵、無塵數據，采用偏最小二乘回歸法分別建立有塵、無塵狀態下以NDVI(1 298，1 340)，RVI(1 298，1 325)，NDWI(860，1 450)和SIWSI為自變量的茶樹葉片EWT估算模型，并對相同植被指數的有塵、無塵模型R2進行相對變率計算，具體結果見表4。由表4可知，無論有塵與無塵狀態下，所選4種植被指數構建茶樹葉片EWT模型的R2均達到0.7以上，且無塵茶樹葉片EWT估算模型的R2始終大于相同植被指數構建的有塵模型R2；4種植被指數構建的茶樹葉片EWT估算模型在有塵、無塵狀態下其R2大小依次為：RVI(1 298，1 325)>NDVI(1 298，1 340)>NDWI(860，1 450)>SIWSI；其R2相對變率大小為：NDVI(1 298，1 340)

表4 在有塵和無塵狀態下分別建立的茶樹葉片EWT指數估算模型與評價

利用檢驗樣本集數據的有塵、無塵數據，對上述4種植被指數構建的模型進行精度檢驗，分析葉面滯塵對不同指數構建模型精度的影響，結果見表5。由表5可知，以NDVI(1 298，1 340)，RVI(1 298，1 325)，NDWI(860，1 450)和SIWSI為自變量構建的茶樹葉片EWT估算模型，在有塵、無塵狀態下其估算值與實測值線性擬合方程的RMSE均為0.001，R2除SIWSI指數構建的模型外其余均大于0.6。以NDVI(1 298，1 340)構建的模型估算值與實測值擬合方程的R2最大，相對變率最小，但僅有塵狀態下其估算值與實測值相近(線性擬合方程斜率為0.777)，而無塵狀態下估算值與實測值線性擬合方程斜率僅為0.225，表明估算值與實測值相差較大。以NDWI(860，1 450)構建的估算模型估算值與實測值線性擬合方程的R2雖然在有塵、無塵不同狀態下同樣具有較小的相對變率，且在無塵狀態下該模型估算值與實測值線性擬合方程斜率最接近1，但其決定系數較小，在有塵狀態下其斜率值與1相差較大。以RVI(1 298，1 325)構建的模型估算值與實測值線性擬合方程雖然R2相對變率較NDWI(860，1 450)和NDVI(1 298，1 340)大，但在有塵、無塵狀態下其R2均具有較大值(>0.694)，且估算值與實測值線性擬合方程斜率均與1相差小，可見滯塵對以RVI(1 298，1 325)構建的估算模型精度影響小。

表5 茶樹葉片EWT的實測值與估算值比較分析

2.4 滯塵混合狀態下的茶樹葉片含水量高光譜估算模型構建與驗證

自然條件下茶樹葉片處于不同滯塵環境，葉面滯塵狀態的不確定將嚴重影響茶樹葉片水分的準確估算，構建一種對滯塵不敏感的茶樹葉片水分光譜模型，對于無損、快速、準確測定茶樹葉片水分具有重要作用。因此，利用建模集數據中有塵、無塵數據進行隨機混合，并采用偏最小二乘回歸法分別以RVI(1 298，1 325)，NDVI(1 298，1 340)，NDWI(860，1 450)和SIWSI為自變量構建混合狀態茶樹葉片EWT估算模型，建模結果見表6。由表6可知，基于上述4種植被指數構建的茶樹葉片EWT模型的決定系數以RVI(1 298，1 325)最大(R2=0.853)，NDVI(R1 298，R1 340)次之(R2=0.837)，NDWI(860，1 450)和SIWSI最小分別為0.752和0.688。

表6 茶樹葉片EWT在有塵、無塵混合狀態下的指數估算模型

為了檢驗所建模型精度，利用檢驗集樣本(包括有塵、無塵數據)對模型估算值與實測值進行線性擬合分析，結果如圖2。由圖2可知，在混合條件下以RVI(1 298，1 325)，NDWI(860，1 450)，SIWSI，NDVI(1 298，1 340)為自變量構建的模型估算值與實測值線性擬合方程的RMSE均為0.001，其R2依次為：0.728，0.677，0.520，0.447，RPD依次為：1.917，1.344，1.759，1.443；線性擬合方程斜率分別依次為：0.813，0.776，0.715和0.693，線性擬合方程截距依次為：0.003，0.004，0.005和0.005。比較4種植被指數構建模型的估算值與實測值線性關系可知，以RVI(1 298，1 325)為自變量構建的茶樹葉片EWT模型的估算值與實測值線性擬合方程的R2和RPD最大，斜率與1差值最小，方程截距最小。因此，該模型受滯塵影響小，是混合滯塵狀態下的最優模型，該結果也驗證了RVI(1 298，1 325)受滯塵的影響最小的結論。

圖2 混合條件茶樹葉片水分含量實測值與預測值比較分析

3 結 論

通過分析不同植被指數對茶樹葉面滯塵的敏感性，發現NDVI(1 298，1 340)，RVI(1 298，1 325)，NDWI(860，1 450)，SIWSI與EWT的相關性高，且有、無塵狀態下相關系數的相對變率小。選擇這4個指數構建EWT估算模型并分析滯塵對EWT估算精度的影響，利用偏最小二乘回歸法分別建立有塵、無塵茶樹葉片水分估算模型，發現滯塵會降低茶樹葉片水分估算精度，且4個模型中在有塵、無塵兩種狀態下，以NDVI(1 298，1 340)，RVI(1 298，1 325)為自變量的模型估算精度高、反演效果優于NDWI(860，1 640)、SIWSI。在有塵、無塵混合狀態下以RVI(1 298，1 325)為自變量的茶樹葉片水分估算模型精度最高(模型為y=0.245x-0.241)，模型估算值與實測值具有較強的一致性，反演效果最佳，因此RVI(1 298，1 325)構建的茶樹水分估算模型在自然滯塵狀態下對茶樹葉片含水量的精確估算具有較大潛力，能夠為遙感估測有塵、無塵以及混合狀態下茶樹葉片水分含量提供參考依據，對茶樹精準管理具有重要的指導和參考價值。