雙螺旋結構電容式棒位測量傳感器偏心性能研究

李彥霖，秦本科，薄涵亮

(清華大學 核能與新能源技術研究院，北京 100084)

控制棒是核反應堆關鍵的功率控制部件，在正常工況下，反應堆的啟動、關停與功率調節均需通過調整控制棒棒位來實現，在事故工況下，控制棒快速落棒可實現反應堆的緊急停堆。因此，控制棒棒位的準確監測直接關系到反應堆的安全性和可靠性。

壓水堆核電廠多采用基于電磁感應原理工作的線圈編碼式棒位測量傳感器[1]，該種傳感器通過對分組編碼線圈輸出信號的處理得到GRAY碼形式的數字信號，并由此對應出控制棒棒位，這種傳感器具有較強的抗干擾能力，指示精度最高可達±3步，缺點是系統結構復雜、可靠性較低且難以實現棒位的連續測量。高溫氣冷堆的棒位測量傳感器為自整角機式[2]，該種傳感器通過測量電機輸出軸的角位移獲得控制棒的線位移，測量精度最高可達±4 mm，缺點是系統響應速度較慢、加工精度要求高且檢驗、標定較為困難。此外還有多種基于不同測量原理制成的棒位測量傳感器，如超聲波式[3]、磁致伸縮式[4]等。

電容式傳感器具有高可靠性、低成本等優點被廣泛應用于工業測量領域，具有雙螺旋結構特征的電容式傳感器在工業管道物相濃度檢測[5-6]、物位測量[7]、ECT成像[8]等方面已有較多應用。200 MW核供熱堆采用內置式控制棒水力驅動技術[9]，棒位測量傳感器是該驅動系統的關鍵部件之一，清華大學薄涵亮教授課題組首先將電容式傳感器應用于內置式棒位測量，并提出了兩種不同極板結構的棒位測量傳感器方案，分別為直線極板型[10]和雙螺旋極板型[11]。對于直線極板型傳感器，由于被測桿和傳感器內壁存在間隙，在棒位一定的情況下，被測桿偏離傳感器中心軸將導致傳感器電容與被測桿無偏移時不同，該電容變化量引起的誤差稱為偏心誤差，被測桿向不同方向偏移同一程度引發的電容變化量也不相同，稱為偏心不一致現象。雙螺旋極板型棒位測量傳感器能有效克服偏心不一致現象，即被測桿沿任意方向偏移同一距離與被測桿無偏移時的電容變化量相同，但該電容變化量導致的偏心誤差依然超過了傳感器實際使用限值。由于核供熱堆控制棒步進單位為15 mm，棒位測量傳感器的最大允許測量誤差為±7.5 mm，關于電容式棒位測量傳感器偏心問題的描述詳見文獻[12]。

本文采用有限元程序COMSOL Multiphysics，建立雙螺旋結構電容式棒位測量傳感器的計算模型并進行實驗驗證，結合正交試驗設計方法，系統研究傳感器設計參數和偏心誤差的相關關系。

1 傳感器結構與計算模型

1.1 傳感器設計方案

雙螺旋結構電容式棒位測量傳感器的結構示意圖如圖1所示。傳感器主要由4部分構成：兩塊螺旋狀金屬極板(分別為激發電極和測量電極)、絕緣陶瓷管、屏蔽層和控制棒被測桿。螺旋狀金屬極板張角α=170°，極板螺距H=53.59 mm，傳感器和被測桿全長D=1 000 mm。測量過程中被測桿沿絕緣陶瓷管內壁所形成的環形腔做軸向運動，引起兩塊螺旋極板間電勢分布函數和電容的變化，被測桿采用不銹鋼材料，在測量過程中全程接地，被測桿半徑R1=7 mm，絕緣陶瓷管內外半徑分別為R2=8 mm、R3=11 mm，相對介電常數εr1=9.6，屏蔽層半徑R4=13 mm。

圖1 雙螺旋結構電容式棒位測量傳感器示意圖

1.2 計算模型及邊界

以拉普拉斯方程為基礎，構建描述雙螺旋結構電容式棒位測量傳感器的理論求解模型。通常假定傳感器檢測場空間內無自由分布電荷，檢測場的電勢分布函數φ(x,y,z)滿足泊松方程，即：

(1)

式中：ε0為自由空間相對介電常數；ε(x,y,z)為隨空間坐標變化的相對介電常數分布函數。給定式(1)的定解條件，在激發電極上施加1 V的激勵電壓，測量電極、金屬被測桿與外屏蔽層接地，電勢均為0 V，如式(2)所示：

(2)

由式(1)、(2)解得空間電勢分布函數后，在檢測電極S感應出的電荷量Q由式(3)計算：

(3)

極板間的電容C為電荷量和電勢差U的比值，即式(4)：

(4)

由于該傳感器邊界形狀復雜，且電容傳感器的檢測場屬于一種“軟場”[13]，可利用有限元方法對該問題進行有效求解。采用有限元方法求解傳感器電容時，物理場采用COMSOL程序AC/DC模塊中靜電單元建立，求解過程包括建立傳感器模型、添加材料屬性(相對介電常數)、施加邊界條件、網格劃分與后處理5個過程，在傳感器4部分結構中，將激發電極定義為終端并施加1 V的電壓，對檢測電極、被測桿和屏蔽層施加接地邊界，同時在傳感器模型外建立空氣域并指定為無限元域以消除模型中空氣域體積對計算結果的影響，定義陶瓷管相對介電常數為9.6。

2 實驗系統與模型驗證

2.1 實驗系統簡介

計算模型驗證采用雙螺旋結構電容式棒位測量傳感器與接地金屬介質桿的線性度實驗[14]，電容式棒位測量傳感器測量系統的實驗平臺主要由5部分構成，分別為電容式棒位測量傳感器、控制棒被測桿、用于棒位信息校準的光柵線位移傳感器(測量精度為±0.005 mm)、用于電容測量和棒位指示的棒位測量樣機和數據采集處理程序，該實驗平臺的結構組成如圖2所示。

圖2 電容式棒位測量傳感器實驗平臺

在對電容式棒位測量傳感器的靜態特性實驗過程中，被測桿以一定的步進長度在傳感器中移動，光柵線位移傳感器跟隨被測桿運動并提供棒位真值，棒位測量樣機將對被測桿處于相應步數時傳感器的電容進行測量并通過數據采集處理程序顯示電容檢測信息，隨后可通過測量得到的各棒位處的電容分布情況換算得出被測桿所處的棒位。

2.2 計算模型驗證

依據傳感器實際結構，在程序中建立了相應的分析模型，實驗室所制成的傳感器有效量程為0～840 mm，其余設計參數如本文1.1節所述。首先對計算模型進行網格無關性驗證，分別采用程序中提供的較細化、超細化和極細化3種方式進行網格剖分，被測桿處于0 mm棒位時，上述3種網格剖分方式所得的域單元數量分別為28.96萬、61.52萬和829.20萬，由3套網格計算得到的電容分別為312.02、308.85、305.53 pF，與第3套網格相比，前兩套網格電容計算結果的相對誤差分別為2.12%和1.08%，在考慮計算精度和計算速度的前提下，認為采用超細化的網格劃分方式較為合理。利用實驗結果驗證計算模型，在傳感器0～840 mm量程范圍內，該實驗以100 mm為1個步進單位，共測量得到了9個棒位的電容，計算模型的步進單位與實驗一致，將實驗結果與模型計算結果0 mm棒位處電容進行置零處理后，計算模型驗證情況如圖3所示，實驗得到的9個數據點全部落入模型計算結果的±10%誤差帶內。實驗結果和模型計算結果得到的傳感器靈敏度分別為-0.036 9 pF/mm和-0.037 9 pF/mm，兩者相對誤差為2.71%，表明該計算模型合理可靠。

圖3 模型計算結果與實驗結果對比

3 優化設計與結果分析

3.1 目標函數確定與偏心規律分析

定義靈敏度最大變化量Nu為優化過程的目標函數，首先給出傳感器靈敏度S的定義，如式(5)所示。

S=ΔC/ΔX

(5)

式中：ΔX為棒位變化量；ΔC為由ΔX引起的傳感器電容變化量。靈敏度最大變化量Nu的定義由式(6)給出：

(6)

隨著被測桿偏心位移L的變化，傳感器靈敏度S將發生變化，L的取值范圍為0～1 mm，0 mm對應被測桿與傳感器中心軸重合，1 mm對應被測桿與陶瓷管內壁完全貼合。S0為L=0 mm，即無偏心時的靈敏度，Smax為隨偏心位移L變化時所能得到的與S0相對變化量最大的值，式(6)用于描述由于被測桿偏心所引起的傳感器最大靈敏度偏差。假設計算模型非線性誤差可忽略(計算模型中被測桿無偏心時隨棒位變化的最大非線性誤差為0.81 mm，可忽略)，Ct為被測桿在靈敏度最大變化量處的電容，Cs為被測桿無偏心時的電容，二者均為棒位函數，如式(7)所示。其中C0為0 mm棒位的傳感器電容，X為棒位深度，取值范圍為0～1 000 mm。

(7)

隨棒位變化的最大偏心誤差N可由Nu與X的乘積直接得到，即式(8)所示。

(8)

首先分析隨偏心位移L變化的傳感器靈敏度分布規律，假定被測桿發生偏心時與傳感器中心軸保持平行，L的計算范圍為0～1 mm，以0.1 mm為單位，利用上述有限元模型得到的計算結果如圖4所示。

圖4 隨偏心位移變化的靈敏度分布

可得知，靈敏度絕對值隨偏心位移L的增加而增加，L取1 mm時，靈敏度絕對值達到最大，被測桿無偏心時靈敏度絕對值為最小值，由此可將靈敏度最大變化量Nu寫成式(9)。其中S1為L取1 mm時的傳感器靈敏度。

(9)

3.2 極板參數分析

目前傳感器所采用的極板張角為170°，固定傳感器其他設計參數不變，分析極板張角對靈敏度最大變化量的影響，計算區間為10°～170°，以20°為單位，有限元模型得到的計算結果列于表1。

表1 隨極板張角分布的靈敏度最大變化量

從表1可知，隨著極板張角的減小，靈敏度最大變化量單調下降，在傳感器其他設計參數保持不變的情況下，當極板張角為10°時，靈敏度最大變化量達到最小值，表明較小的極板張角有助于減小偏心誤差。

目前傳感器極板所采用的螺距H=53.59 mm，固定傳感器其他設計參數不變，分析螺距對靈敏度最大變化量的影響，計算區間為100～400 mm，以100 mm為單位，有限元模型得到的計算結果列于表2。

表2 隨極板螺距分布的靈敏度最大變化量

從表2可知，螺距從53.59 mm增大到100 mm時，靈敏度最大變化量下降最快，隨后靈敏度最大變化量下降趨勢減緩。在400 mm的螺距變化范圍內，靈敏度最大變化量隨螺距的增大單調遞減，表明適當增大螺距有助于減小偏心誤差。

3.3 管壁參數分析

目前傳感器所采用的管壁厚度為3 mm，固定傳感器其他設計參數不變，分析管壁厚度對靈敏度最大變化量的影響，計算區間為1～5 mm，以1 mm為單位，此處取徑極比的概念來描述管壁厚度[15]，徑極比ρ=R2/R3，即陶瓷管內半徑和外半徑的比值，所設置的5個厚度參數的ρ=0.889、0.800、0.727、0.667、0.615。有限元模型得到的計算結果列于表3。

表3 隨陶瓷管壁厚度分布的靈敏度最大變化量

從表3可知，隨著管壁厚度的增加(ρ減小)，靈敏度最大變化量呈單調遞減，表明適當增加管壁厚度有助于減小偏心誤差。

目前陶瓷管的相對介電常數為9.6，固定傳感器其他設計參數不變，分析陶瓷管相對介電常數對靈敏度最大變化量的影響，計算取值為7、5、3，有限元模型得到的計算結果列于表4。

表4 隨管壁相對介電常數分布的靈敏度最大變化量

從表4可知，靈敏度最大變化量隨管壁相對介電常數的減小而單調遞減，表明較小的管壁相對介電常數有助于減小傳感器的偏心誤差。

3.4 結構參數的正交優化設計

電容式棒位測量傳感器的優化過程涉及到4個相關參數，進行全參數組合分析難以實現，所以選用正交試驗設計方法對傳感器的4個參數進行正交組合優化分析。該正交表共設置了4個因素，每個因素共設置了3個水平，正交表按照L9(34)的方式構造，所設計的傳感器參數組合和相關計算結果列于表5。

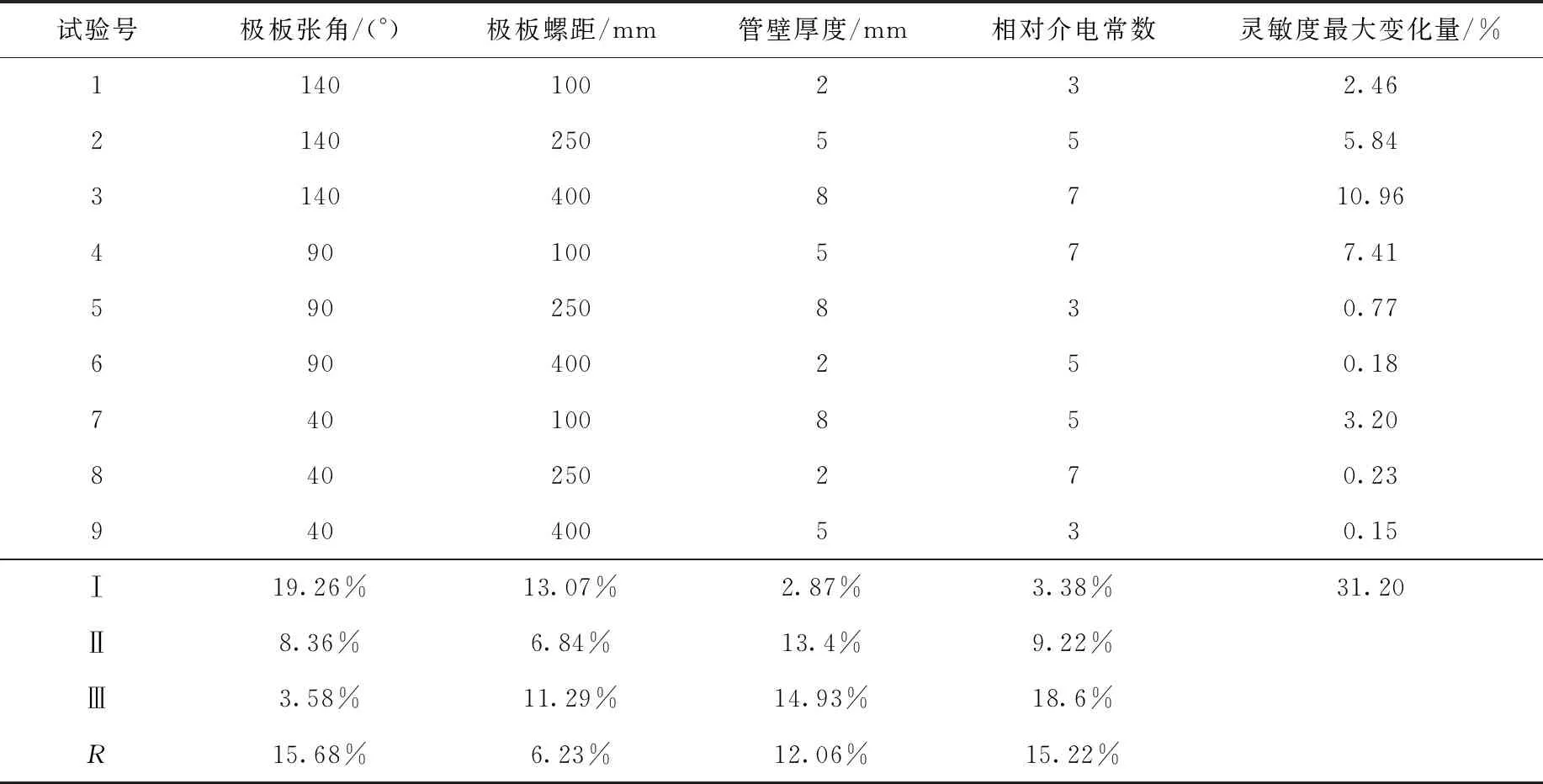
表5 正交試驗表及結果

如表5所列，由于正交表的綜合可比性，極差R的大小可用來比較各因素由于“水平”差異對試驗結果的影響程度，即對傳感器靈敏度最大變化量而言，各參數的影響程度排序如下：極板張角>管壁相對介電常數>管壁厚度>螺距。依據各因素對應的Ⅰ、Ⅱ、Ⅲ的大小，可確定各因素取哪個水平較好。由于靈敏度最大變化量越小越好，因此可得到1組優化參數：極板張角=40°，極板螺距=250 mm，管壁厚度=2 mm，相對介電常數=3。

在正交表所列出的9種傳感器設計方案中，共有3組能夠滿足偏心誤差要求，分別是第6組、第8組和第9組，上述3組方案傳感器的靈敏度分別為-0.010 14、-0.005 48、-0.002 86 pF/mm，從保障傳感器靈敏度的角度看，選取第6組方案較為合適，該組設計方案在0～1 000 mm量程范圍內最大偏心誤差為1.81 mm，小于±7.5 mm的允許誤差限值，即不會由于被測桿偏心而導致控制棒棒位誤讀數，電容變化量共有10.14 pF，屬于實驗室儀器能有效分辨的范圍。未進行結構參數優化的傳感器的靈敏度最大變化量為28.44%，在0～1 000 mm量程范圍內最大偏心誤差為284.4 mm，經優化后傳感器測量精度提升明顯，從靈敏度和最大偏心誤差的角度均能滿足實際使用要求。

4 結論

本文建立了雙螺旋結構電容式棒位測量傳感器的有限元計算模型并進行了實驗驗證，結果表明該計算模型具有良好的計算能力，隨后利用該模型分析了極板張角、螺距、管壁厚度和管壁相對介電常數4個參數對靈敏度最大變化量的影響，通過正交試驗設計方法優化了傳感器的設計方案，通過上述研究，主要得到了以下結論：

1) 傳感器設計參數對靈敏度最大變化量的影響程度排序，依次為極板張角>管壁相對介電常數>管壁厚度>螺距；

2) 減小極板張角、增大極板螺距、增大管壁厚度、減小管壁相對介電常數有助于減小偏心誤差；

3) 通過正交試驗設計方法和對計算結果的分析，在正交表選定的參數范圍內找到了能滿足偏心誤差限值的3種設計方案，在這3種設計方案中，第6組所選定的方案在0～1 000 mm量程范圍內共能引起10.14 pF的電容變化量，最大偏心誤差為1.81 mm，該組方案的靈敏度和最大偏心誤差均能滿足實際使用需求。