流動沸騰汽泡脫離直徑尺寸分布研究

何 雯，趙陳儒，薄涵亮，趙崇巖

(清華大學 核能與新能源技術研究院，北京 100084)

由于換熱效率較高，沸騰現象在核反應堆中得到了廣泛應用，沸騰換熱量的計算也一直是研究的熱點[1]。在換熱計算中，廣泛采用RPI模型，該模型將換熱分為蒸發(fā)換熱、瞬態(tài)導熱和對流換熱3部分。蒸發(fā)換熱是指汽泡從生長到脫離帶走的熱量，瞬態(tài)導熱是指汽泡脫離壁面后較冷的液體填充汽泡原來的位置重新形成過熱液層帶走的熱量，而對流換熱則是指由于液體流動所造成的換熱[2]。可見，沸騰換熱與汽泡行為息息相關，研究汽泡動力學參數對計算換熱具有重要的意義。

脫離表示汽泡在核化點生長到一定大小離開核化點的行為，汽泡脫離直徑即指汽泡離開壁面核化點時的直徑，該值的大小將直接影響汽泡蒸發(fā)帶走的熱量[3]。目前，研究汽泡脫離直徑的方法主要有3種，即力平衡法、能量平衡法和經驗關系式法，但由于前兩種方法通常較復雜，且需要的參數較多，如汽泡周圍速度梯度、汽泡生長傾斜角，因此通過考慮影響脫離直徑的因素，進而通過實驗數據擬合經驗關系式的方法被廣泛采納。Basu等[4]和Brooks等[5]通過實驗研究，分析了壁面熱流密度、液體過冷度、質量流量和系統壓力對脫離直徑的影響，最后得到一套綜合考慮這些因素的經驗關系式。Du等[6]對汽泡進行受力分析，通過大量的實驗數據，發(fā)現這些力的影響可通過普朗克數(Pr)、雅克比數(Jaw)、汽液密度比(ρ*)和汽泡雷諾數(Reb)反映，因此分別提出了一套適用于水平和豎直管道下的脫離直徑關系式。Ren等[7]對窄矩形通道內的汽泡脫離直徑進行了研究，發(fā)現與壁面過熱度、液體過冷度、質量流量相比，壓力對脫離直徑的影響可忽略不計，因此得到的經驗關系式僅是雅克比數和雷諾數的函數。可見，目前已有較多的經驗關系式用于預測流動沸騰下汽泡脫離直徑的平均值。

然而，沸騰是一非常復雜的換熱過程，大量實驗表明，在相同工況下，不同核化點的脫離直徑存在區(qū)別，即使同一核化點產生的脫離直徑也會大小不一，一些大氣泡雖占比較少，但對于換熱的貢獻不可忽略，因此，僅采用一個平均值來反映脫離直徑會對換熱計算造成較大的誤差[8-9]。Abdelmessih等[8]研究了液體流速對汽泡生長和破滅的影響，然后將同一核化點汽泡尺寸大小不一的原因歸因于液體中的渦流。Klausner等[10]觀察到汽泡脫離直徑呈正態(tài)分布，并認為壁面過熱度和汽泡質心處液體速度的正態(tài)分布是汽泡直徑呈正態(tài)分布的主要原因。Kaiho等[9]通過實驗得到22組不同工況下的流動沸騰汽泡脫離直徑分布，每組分布基于200個以上的汽泡，實驗發(fā)現這些分布的標準差均值是脫離直徑均值的0.51倍，因此認為脫離直徑的分布不可忽略，并發(fā)現伽馬分布用于該分布的擬合準確度更高。Yoo等[11]研究了不同軸向位置的脫離直徑尺寸分布，并分析了壁面過熱度、熱通量、過冷度和質量流量對尺寸分布的影響，實驗發(fā)現正態(tài)分布的擬合準確度更高。張旺[12]和杜靜宇[13]同樣采用正態(tài)分布，其中杜靜宇通過對大量數據的分析，認為脫離直徑分布的標準差為0.131這一定值，并對其進行了驗證，但實際上這種方法忽略了質量流速、過熱度等一系列因素的影響，不具有廣泛的適用性。

綜上，流動沸騰下的汽泡脫離行為是一個復雜的過程，呈現某種概率分布，如果僅采用一個均值來描述脫離直徑，不僅忽略了壁面過熱度、液體流速的隨機性對脫離直徑的影響，還會對換熱計算造成較大的誤差。因此，有必要對流動沸騰下脫離直徑的尺寸分布做進一步研究，進而充分認識汽泡脫離行為，提高后續(xù)換熱計算的準確性。

1 汽泡分布描述

汽泡脫離直徑(Dd)的概率密度函數(PDF)是指不同直徑范圍內的汽泡數占總汽泡數的比例呈現的函數分布，如正態(tài)分布、伽馬分布，而累計分布函數(CDF)則是指概率密度函數的積分。對于概率函數的選擇，Kaiho等[9]對22組實驗數據進行分析，發(fā)現伽馬函數(Gamma)的誤差為6.98%，而正態(tài)分布函數(Gaussian)的誤差為14.8%，因此認為伽馬函數準確度更高，但杜靜宇[13]則認為當數據足夠多時，正態(tài)分布函數能更準確地描述脫離直徑的分布，Yoo等[11]、張旺[12]同樣發(fā)現正態(tài)分布函數準確度更高，而Ooi等[14]則認為函數的選擇和壓力有關，低壓下對數正態(tài)分布或伽馬分布準確度更高，高壓下正態(tài)分布更高，但該結論僅適用于水。可見，概率密度函數的選擇尚無確定的結論，當工質不僅為水時，函數的選擇還需進一步確定。

因此，本文選擇60組不同工況下的汽泡尺寸分布實驗數據，每組實驗得到的分布均是基于大量的重復實驗，具體工況列于表1[9,11,15-17]，其中μ和σ分別為這組分布的均值和標準差。由前文可知，在尺寸分布的描述中采用較頻繁的兩種概率密度函數分別為伽馬函數和正態(tài)分布函數，表1列出了部分工況的具體實驗條件以及兩種概率密度函數的擬合誤差，圖1則對兩種函數應用到其中兩組工況(工況3、14)的準確性進行了詳細比較。可發(fā)現，伽馬函數和正態(tài)分布函數均能較準確地描述脫離直徑尺寸分布，但兩者的相對準確性還有待進一步確定。

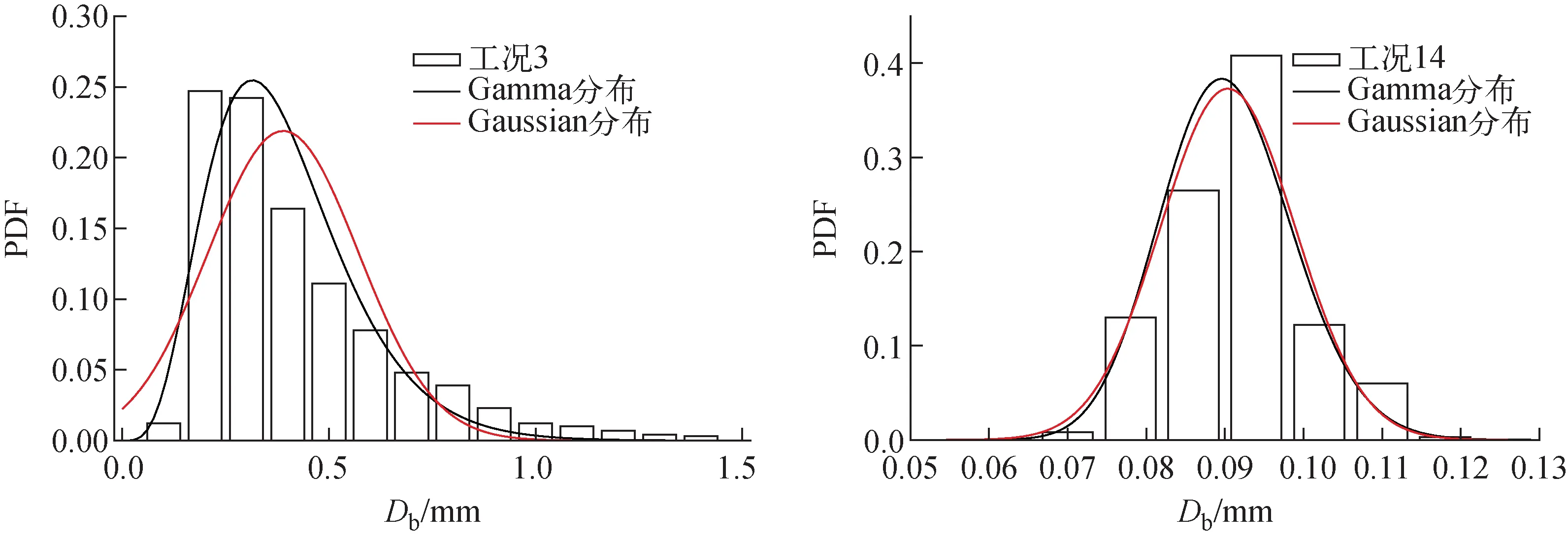
圖1 伽馬函數和正態(tài)分布函數誤差對比

為比較兩種函數應用于流動沸騰汽泡脫離直徑尺寸分布的準確性，本文采用累計分布函數計算誤差，具體定義[9]如下：

(1)

其中：ER為平均絕對誤差；nb為數據點數；CDFfit,j為第j個數據點的擬合值；CDFexp,j為第j個數據點的實驗值。

表1后兩列為該工況下兩個函數的誤差。根據對比分析，本文得到伽馬函數的平均絕對誤差(ERGamma)為27.5%，正態(tài)分布函數的平均絕對誤差(ERGaussian)為23.7%。可發(fā)現，在本文數據范圍內，正態(tài)分布函數和伽馬函數準確度差異不大，相較之下，正態(tài)分布函數準確度更高。兩種函數擬合不同工況時PDF和CDF的誤差示于圖2，因此，本文采用正態(tài)分布函數描述汽泡尺寸分布。

表1 部分工況下的脫離直徑尺寸分布

圖2 概率密度函數誤差對比

2 結果與討論

2.1 概率密度函數

本文選擇正態(tài)分布函數來描述流動沸騰下的汽泡脫離直徑分布，函數表達式如式(2)所示。其中x為自變量，μ和σ是決定函數特征的兩個重要參數。均值μ通常表示出現頻率最高的值，標準差σ則表示數據與平均值的偏離程度，決定分布函數的展寬。因此，為得到脫離直徑在不同工況下的分布情況，可分別對均值和標準差進行確定。

(2)

脫離直徑的均值即指某一工況下脫離直徑出現頻率最高的值，通常也是經驗關系式預測的值，常見關系式的具體形式列于表2。通常，汽泡脫離直徑隨壁面過熱度的增大而增大，隨液體流速和過冷度的增大而減小，原因在于壁面溫度升高可增大汽泡生長速率，進而增大汽泡生長力，有利于汽泡附著于壁面，而液體過冷度的影響恰好和壁面溫度相反。而當流體流速增大時，促進汽泡脫離的曳力增大，進而脫離直徑變小。可見，大多數現有經驗關系式都考慮了這幾個因素的影響，因此，首先對現有關系式進行驗證，對比其應用于本文數據庫范圍內汽泡脫離直徑均值的準確度，絕對誤差ER列于表3，其中由于Yoo和Thorncroft兩個實驗的接觸角未知，因此未對Basu關系式在這兩個實驗下的準確度進行驗證。

表2 常用汽泡脫離直徑經驗關系式

表3 脫離直徑均值預測誤差

可發(fā)現，幾個關系式應用在各組實驗的誤差都較大，且普遍低估了實驗值，其中Du關系式雖然整體誤差很大，但應用于水的準確度較高，誤差主要來源于HFE-301和FC-87工質。經過分析，原因在于Du認為脫離直徑與普朗克數呈3次方增長關系。普朗克數表達式如下：

(3)

其中：cp為比定壓熱容；λ為導熱系數。

但得到這一結論所基于的普朗克數范圍較小(1.027～1.75)，當普朗克數進一步增大后，可發(fā)現脫離直徑與普朗克數并沒有呈現共同增長的趨勢，如圖3所示，這就導致當應用于HFE-301和FC-87時該關系式得到的值遠大于實驗值。因此，為對本文數據庫進行較好的擬合，提高Du關系式在較大普朗克數范圍下的準確度，本文對其進行一定的修正，認為普朗克數對脫離直徑沒有明顯影響，修正后的經驗關系式絕對誤差為25.8%，誤差對比如圖4所示，其中汽泡雷諾數Reb的計算方法同Du，對于豎直管道Dd取0.162 mm，對于水平管道Dd取0.322 mm。

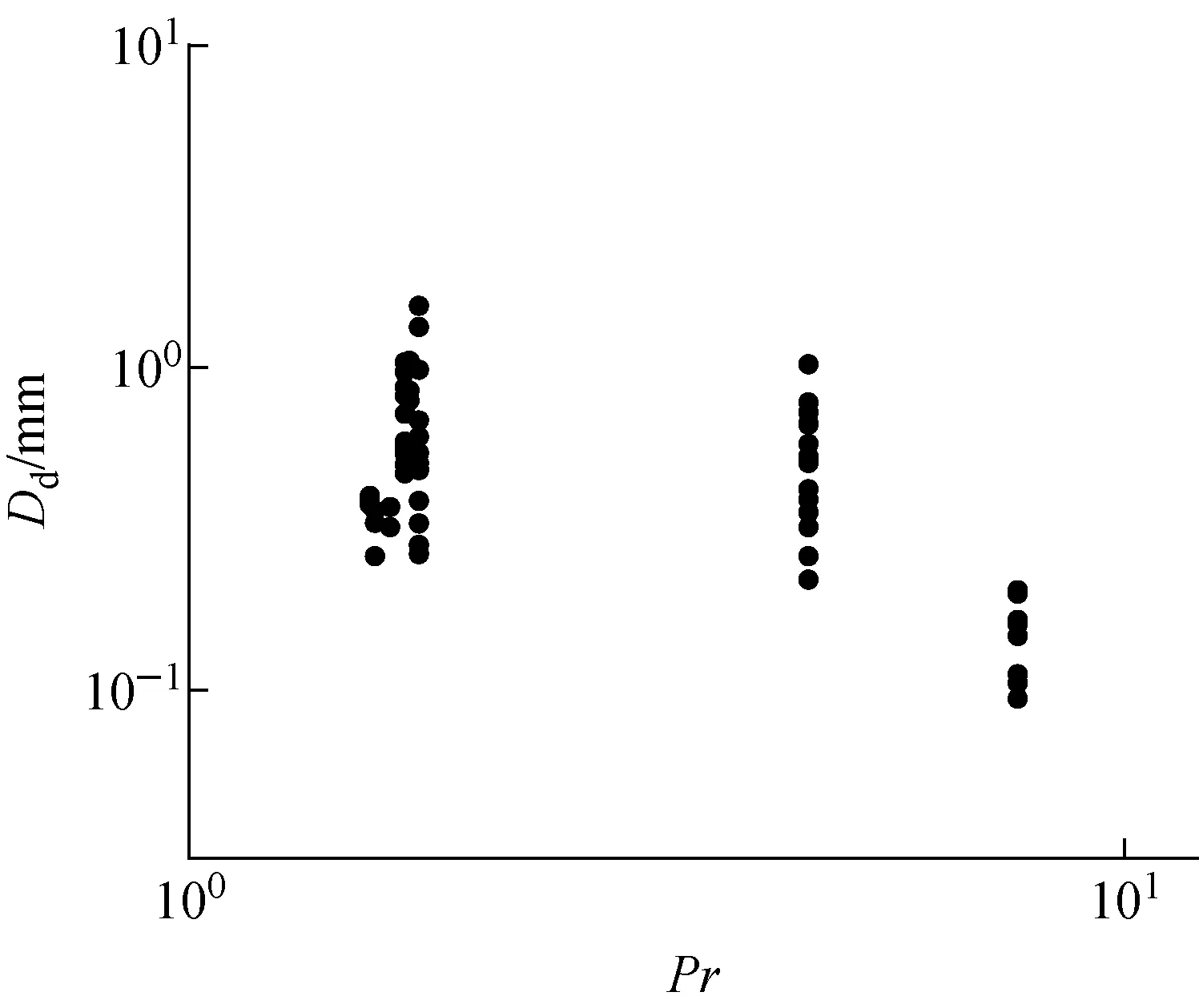
圖3 汽泡脫離直徑隨普朗克數的變化

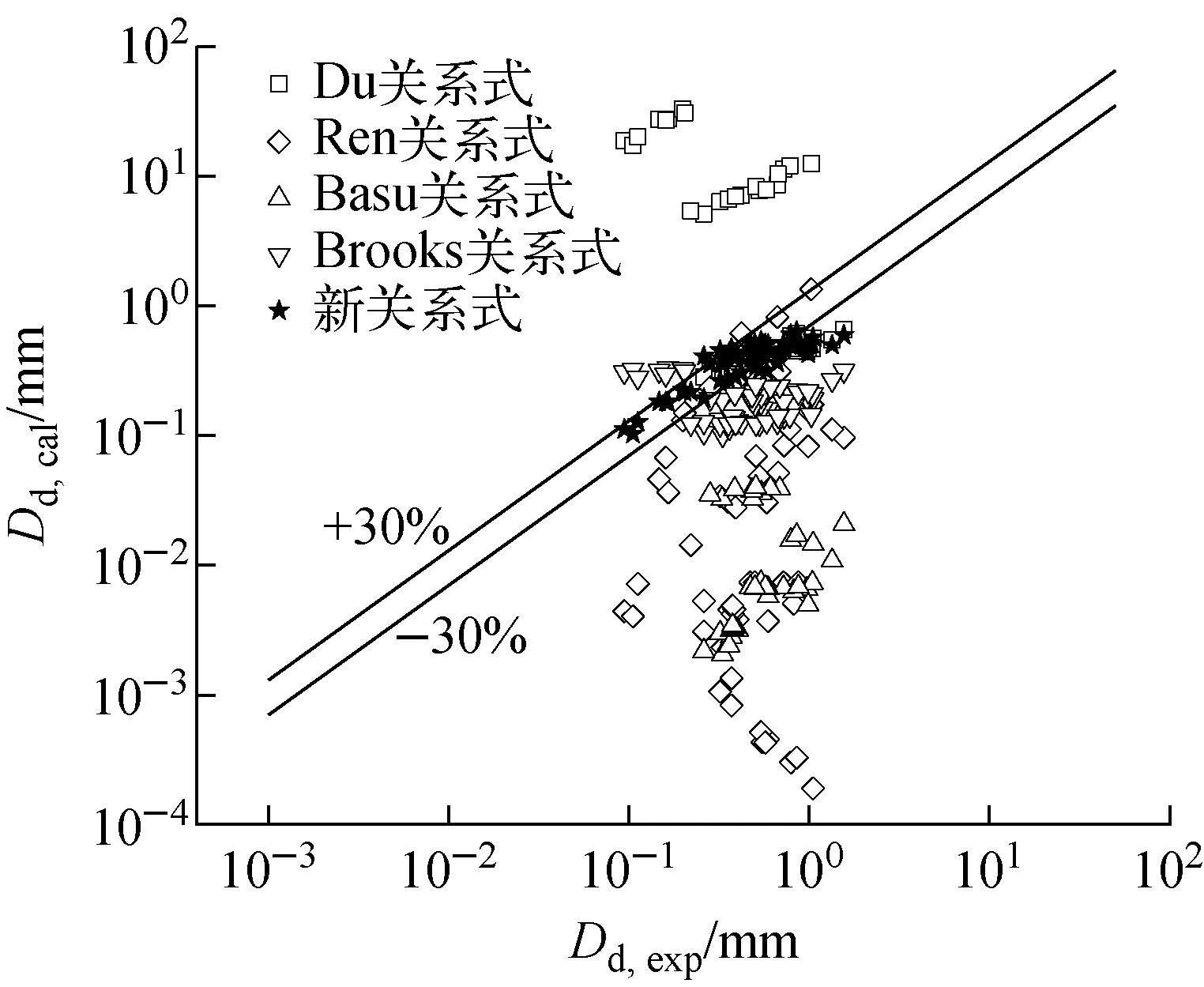
圖4 修正經驗關系式誤差對比

(4)

對于標準差，該值決定了脫離直徑分布曲線的寬度，通常情況下，當正態(tài)分布的均值增大時，曲線會變得更加“矮胖”，標準差也會隨之增加。對于標準差和均值的關系，Kaiho等[9]發(fā)現標準差和均值之比與過熱雅可比數Ja呈正相關，具體形式如下：

(5)

但通過驗證，該關系式在本文數據庫下的絕對誤差為34.6%，還可進一步提高。標準差和均值之比(σ/μ)隨過熱雅可比數、汽泡雷諾數和普朗克數的變化示于圖5。可發(fā)現，σ/μ不僅與雅可比數關系密切，與汽泡雷諾數和普朗克數的關系也不可忽略(式(6))。σ/μ隨汽泡雷諾數的增大而增大，隨普朗克數的增大而減小，兩者分別反映質量流量和物性參數對該比值的影響。基于此，本文通過多次擬合，得到新的標準差經驗關系式，經驗證，新關系式的相對誤差為-0.2%，絕對誤差為21.5%，具有較好預測準確度，具體誤差驗證如圖6所示。

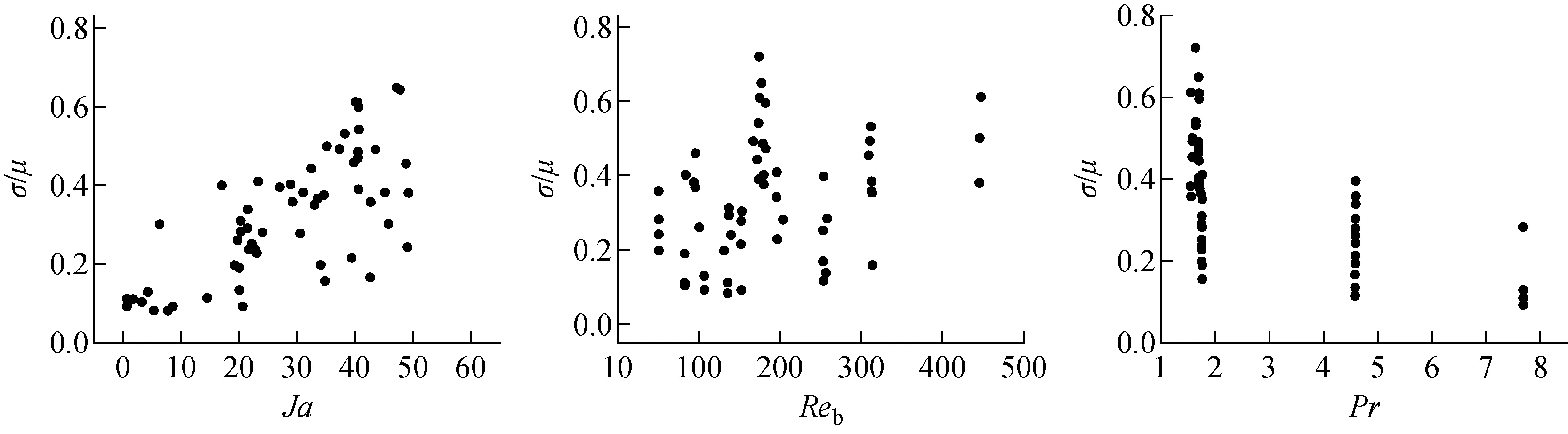
圖5 σ/μ隨無量綱數的變化

圖6 σ/μ誤差驗證

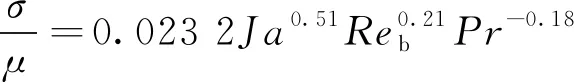
(6)

2.2 驗證

由于本文選取的汽泡尺寸分布數據有限，為驗證方程(2)的準確度，將該關系式應用到Basu[18]、Brooks[5]、Zhou[19]、Colgan[20]和尚靖武[21]等的實驗數據中，如圖7所示，具體實驗工況列于表4，總的絕對誤差為33.8%。因此，可認為方程(2)能較準確地預測不同工況下流動沸騰汽泡脫離直徑的均值。此外，分別選擇不同工況下的水、HFE-301和FC-87驗證方程(2)和方程(6)同時應用于汽泡脫離直徑分布的準確性，誤差(圖8)均在可接受范圍內，FC-87誤差相對較大的原因在于該實驗工況下汽泡脫離直徑的范圍較小(0.1～0.2 mm)，可見分布函數的準確度對均值和標準差的預測值非常敏感。

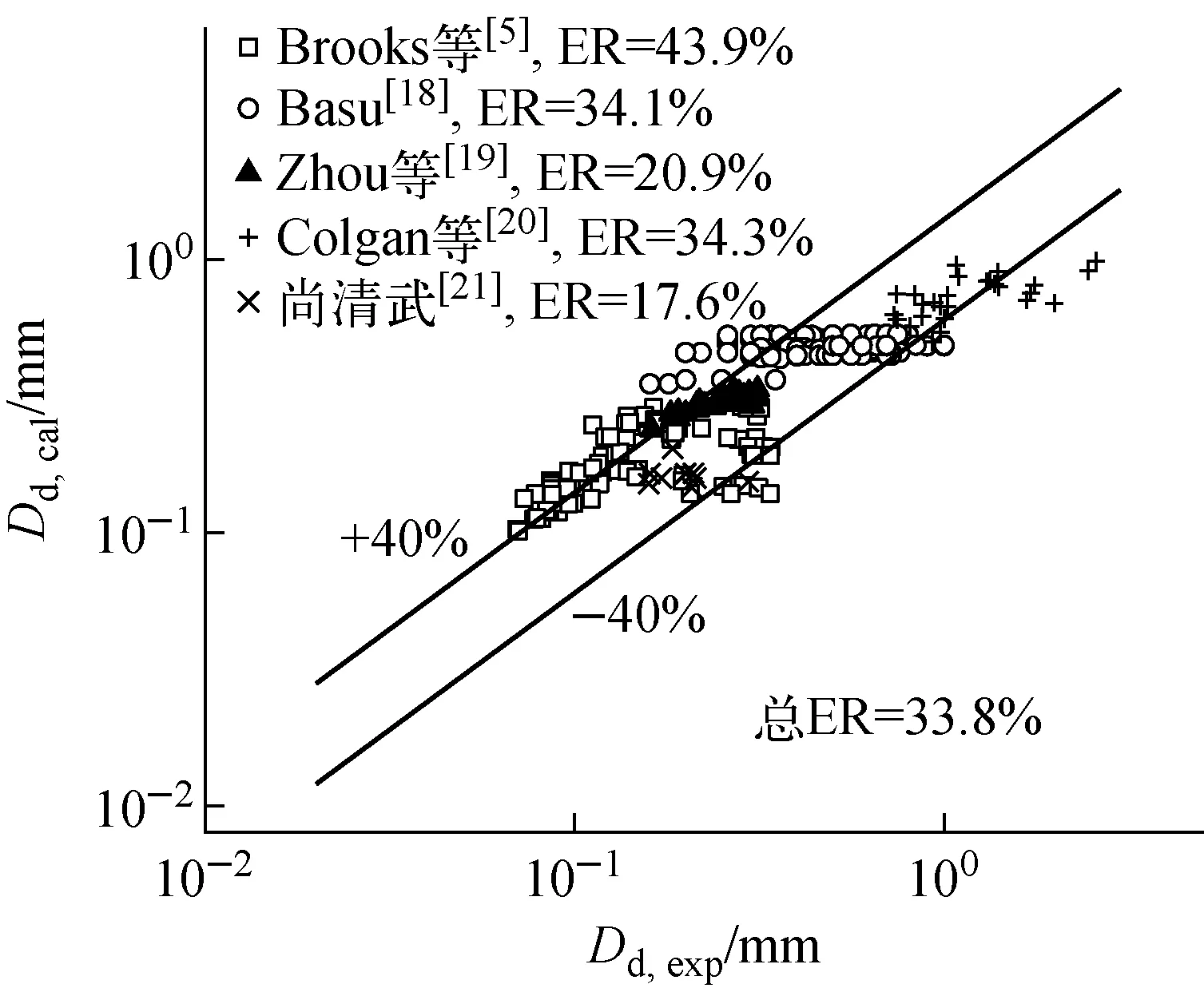
圖7 脫離直徑均值新關系式的準確度驗證

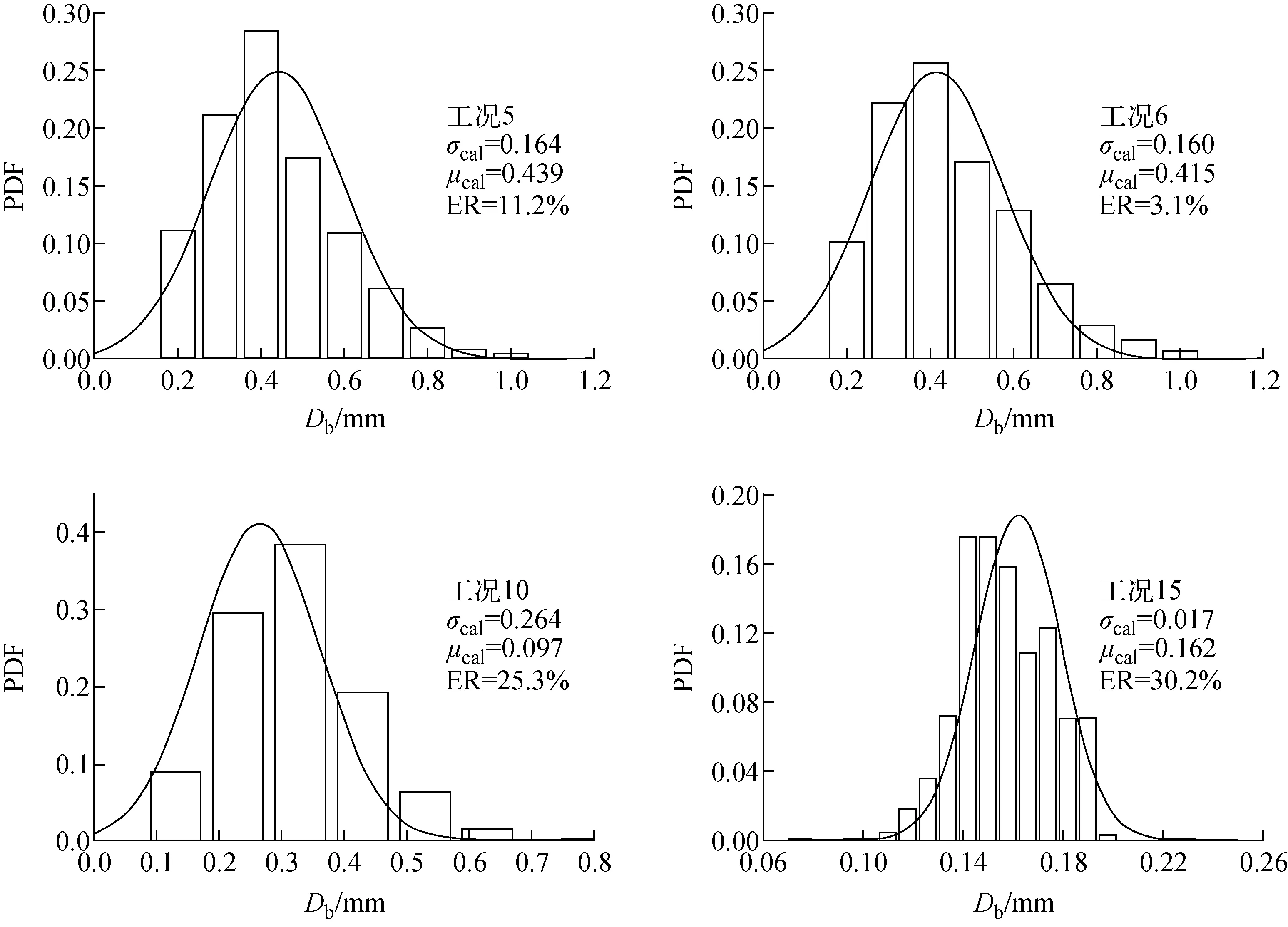
圖8 新經驗關系式誤差驗證

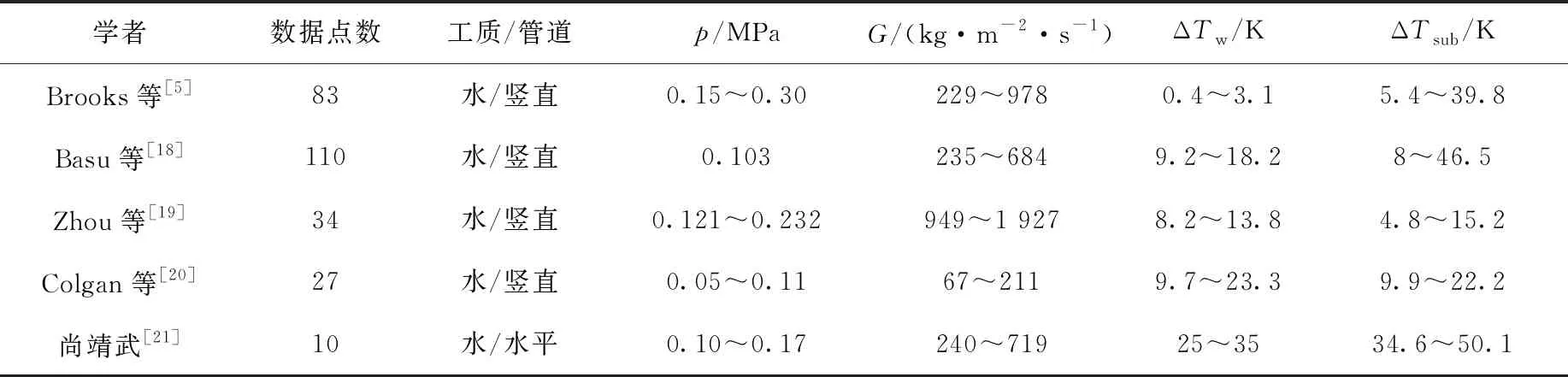
表4 脫離直徑實驗數據范圍

可見，新的經驗關系式能較準確地預測流動沸騰汽泡尺寸分布，關系式的適用范圍列于表5，由于計算尺寸均值的方程(式(4))較計算標準差的方程(式(6))有更多的驗證數據，所以兩者的適用范圍單獨列出。

表5 新經驗關系式適用范圍

3 結論

伽馬分布和正態(tài)分布是兩個常用于描述汽泡尺寸分布的概率密度函數，將兩種分布應用到多組實驗數據中，得到兩者的絕對誤差分別為27.5%和23.7%，因此認為正態(tài)分布更適用于汽泡尺寸分布的描述。正態(tài)分布的兩個重要參數分別為均值和標準差，本文首先對4個現有經驗關系式用于脫離直徑均值計算的準確度進行了評價，發(fā)現誤差均較大，其中Du關系式用于水時準確度較高，但用于普朗特數較高的制冷劑時，準確度大幅下降。因此，本文對Du關系式進行了修正，新關系式不僅能預測本文尺寸分布數據庫中的均值，應用到其他組實驗數據中也具有較高的準確度。此外，分布函數的均值和標準差通常呈正相關，因此本文對標準差和均值的比值進行了擬合，得到的經驗關系式是過熱雅可比數和汽泡雷諾數的函數。最后，得到一套描述流動沸騰汽泡脫離直徑尺寸分布的經驗關系式，該關系式考慮了壁面過熱度、質量流速等的影響。