鉛鉍冷卻快堆含繞絲燃料組件子通道程序開發與驗證

劉佳泰，彭天驥,3，蘇興康，顧 龍,4,*

(1.中國科學院 近代物理研究所，甘肅 蘭州 730000；2.中國科學院大學，北京 100049；3.先進能源科學與技術廣東省實驗室，廣東 惠州 516003；4.蘭州大學，甘肅 蘭州 730000)

中國加速器驅動嬗變研究裝置(CiADS)由直線加速器、散裂靶和次臨界反應堆組成[1]，其中次臨界反應堆選用液態鉛鉍(LBE)冷卻快堆[2]。鉛鉍冷卻快堆具有較高的安全性和可持續性等優點，然而受限于LBE非線性的湍流普朗特數以及LBE具有腐蝕性等困難，通過實驗獲得堆芯的精細熱工水力參數所需要滿足的條件十分嚴格。CFD的幾何刻畫精細，但對整個堆芯或燃料組件進行網格劃分和數值計算需要大量的計算資源，計算時間較長。子通道分析方法通過將燃料組件劃分為內通道、邊通道和角通道，將經驗關系式代入單個子通道的守恒方程中使方程組封閉，迭代求解獲得一定精度的熱工水力參數，可大幅減少精細計算時間。

對于液態金屬，國內外開發了許多適用于含繞絲燃料組件的子通道程序。早期多是基于鈉冷快堆，如ASFRE-Ⅲ[3]基于分布阻力模型對鈉冷快堆進行計算；MATRA-LMR[4]是基于壓水堆程序MATRA開發的鈉冷快堆子通道程序；COBRA-WC[5]和COBRA-LM[6]均是基于美國西北太平洋實驗室開發的COBRA程序改進成的鈉冷快堆程序。近年來針對鉛鉍冷卻快堆的研究日益增多，如SACOS-PB[7]可計算鉛冷快堆穩態條件下的溫度分布；ANTEO+[8]是一種適用于液態金屬強制對流的通用程序。目前已有的液態金屬子通道程序由于使用的關系式不同，具有不同的適用條件和限制，是否適用于CiADS的子通道分析需進一步驗證。

本文開發適用于鉛鉍冷卻快堆的子通道程序，對液態鉛鉍的摩擦阻力模型、湍流交混模型和對流換熱模型進行適用性分析，并與含繞絲燃料組件的LBE大渦模擬(LES)計算結果和傳熱實驗結果進行對比驗證。

1 守恒方程及本構關系

本研究以鉛鉍冷卻快堆含繞絲燃料組件為研究對象，采用子通道分析程序對穩態強迫對流工況下冷卻劑及包殼表面的溫度分布進行計算。程序基于Fortran平臺進行開發，由于LBE在正常工況下不會產生沸騰，因此采用單相流狀態下的守恒方程。

1.1 質量守恒方程

(1)

式中：A為軸向流動面積；ρ為冷卻劑密度；t為時間；m為軸向質量流量；z為軸向控制體高度；eik為符號函數，i為子通道的編號，k為子通道i周邊的間隙；w為單位長度橫向質量流量。方程各項分別為質量隨時間的變化、軸向質量流量隨空間的變化和間隙處的橫向質量流量。

1.2 軸向動量守恒方程

(2)

式中：U為軸向流速；p為壓力；g為重力加速度；θ為冷卻劑通道與垂直方向的夾角；f為摩擦阻力系數；D為燃料棒直徑；K為形阻系數；fT為湍流動量交換系數；w′為單位長度湍流交混流量。方程左邊3項分別為軸向動量隨時間的變化、軸向動量通量隨空間的變化和橫流導致的橫向動量變化。方程右邊分別為壓力項、重力項、摩擦力項和湍流交混項。方程右邊各項共同形成軸向力。

1.3 橫向動量守恒方程

(3)

式中：s為間隙寬度；l為子通道i與子通道k之間的質心距離；KG為橫向阻力系數；Δp為相鄰子通道間的橫向壓差。方程左邊分別為橫向流量隨時間的變化和橫向流量通量隨空間的變化，方程右邊分別為橫向壓差項和間隙阻力項。由于繞絲結構產生橫流，使燃料組件的同一橫截面內具有明顯的壓力差。

1.4 能量守恒方程

(4)

式中：h為流體焓值；PW為燃料棒r面向子通道i的加熱周長；φir為燃料棒r面向子通道i的份額；q為燃料棒的線功率密度；CQ為冷卻劑產熱份額；φin為燃料棒與通道之間的接觸份額；q′為燃料棒傳入冷卻劑的線功率密度；Δh為相鄰通道間焓差；Ck為橫向換熱系數；ΔT為相鄰通道間的溫度差。方程左邊分別為焓隨時間的變化、軸向焓通量隨空間的變化和通道內所有間隙處的橫向焓通量。方程右邊分別為燃料棒傳入流體的熱量、直接在冷卻劑中產生的熱量、湍流交混的熱量和相鄰通道間的熱量交換。

1.5 計算流程

子通道程序在軸向節點的入口沿流向逐步計算。首先通過能量方程更新焓值，之后對質量方程和動量方程聯立的矩陣采用高斯-賽德爾迭代計算得到橫向流量。最后將橫向流量帶入到質量方程計算得到軸向流量，帶入到橫向動量方程計算得到壓力梯度。程序求解流程如圖1所示，主程序在讀取邊界條件和幾何條件后，依次調用物性模塊、能量方程迭代模塊和動量方程迭代模塊完成循環，直到軸向節點全部計算收斂后輸出計算結果。

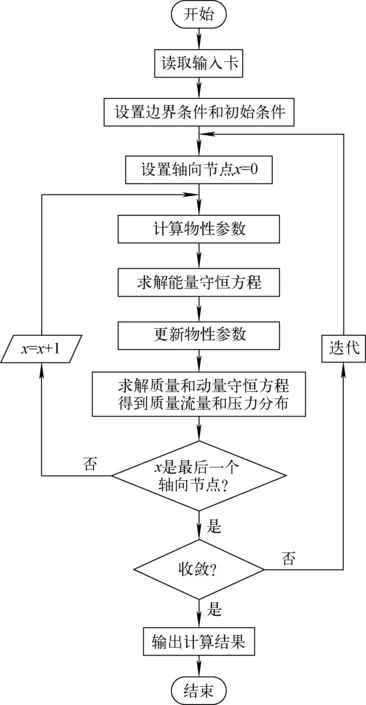
圖1 子通道程序中冷卻劑求解流程

1.6 物性模型

對程序模型進行不確定性分析是評估和驗證模型準確性的關鍵環節。冷卻劑的物性作為模型關鍵輸入參數，在不確定性的傳播過程中起到關鍵作用。冷卻劑相關物性的不確定度列于表1[9]，包括密度、比定壓熱容、動力黏度及熱導率。程序中還需已知冷卻劑的焓值，通過焓的定義計算得到。

表1 LBE的推薦物性關系式

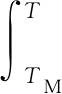
(5)

式中：h0為熔點溫度處的焓值；T為冷卻劑溫度；TM為熔點；cp為比定壓熱容。

1.7 摩擦阻力模型

程序采用達西公式計算壓降：

(6)

式中：L為通道長度；De為通道水力直徑；v為冷卻劑流速。

求解壓降的關鍵是得到合適的摩擦阻力系數f，而摩擦阻力系數一般是雷諾數Re和幾何關系的函數。Fan等[10]以CiADS棒束為原型，開展了阻力系數測量實驗，并將實驗結果與摩擦關系式進行對比。如圖2所示，在3 750≤Re≤16 250范圍內，Rehme關系式[11]能在±10%的范圍對全部54個實驗點準確預測，均方根誤差為7.8%。因此本程序選用Rehme關系式計算摩擦阻力系數：

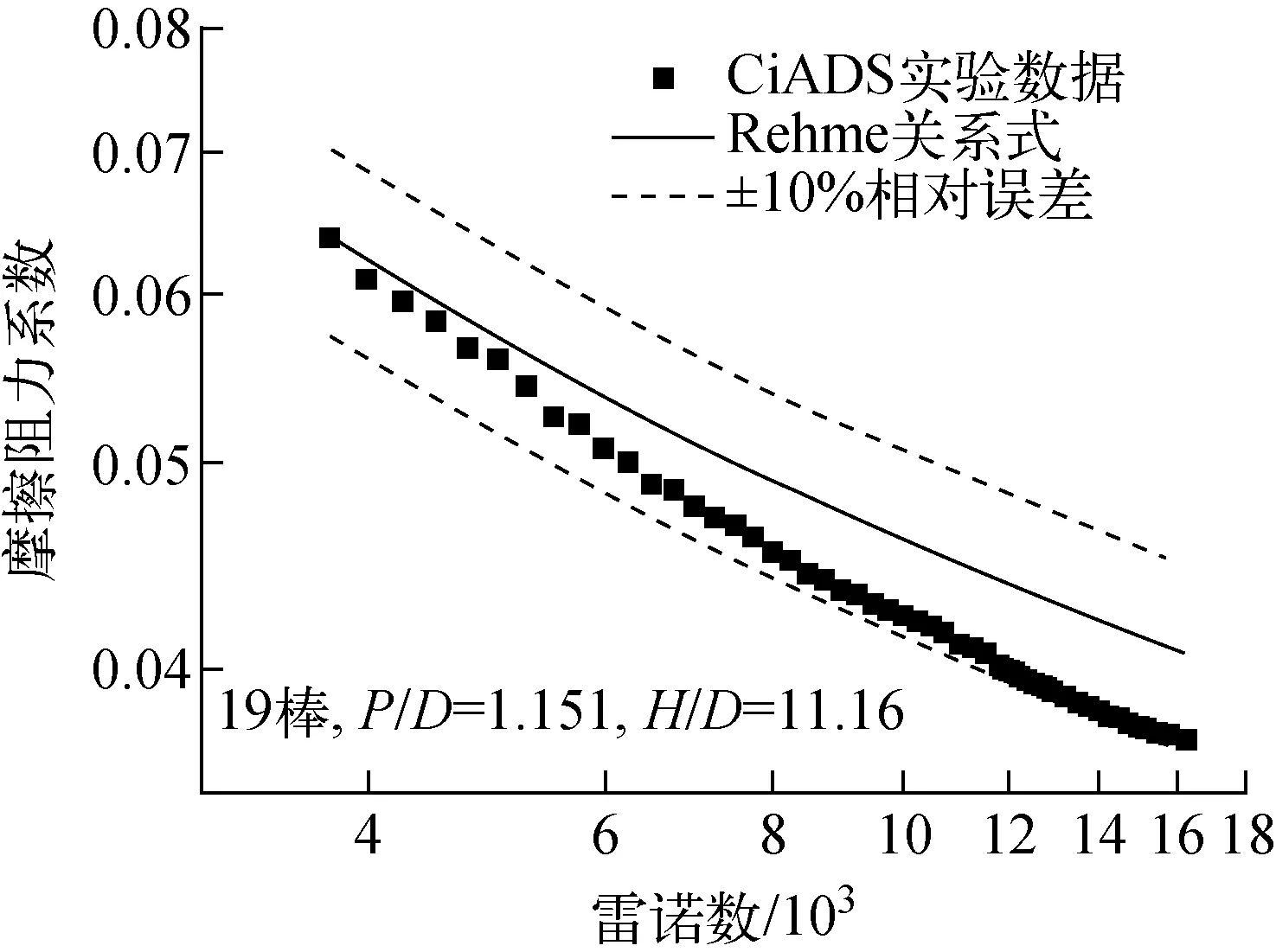
圖2 Rehme關系式與CiADS實驗的摩擦阻力系數對比

(7)

式中：Pwb為棒束濕周；Pwt為總濕周；F為幾何因子，用于考慮繞絲的幾何結構。

(8)

式中：P為相鄰燃料棒質心的距離；Dw為繞絲直徑；H為繞絲螺距。關系式的適用范圍為：103≤Re≤3×105，1.125≤P/D≤1.417，5≤H/D≤50。

1.8 湍流交混模型

繞絲的存在會增加相鄰子通道間的橫向交混，具有展平橫向溫度分布的作用。假設湍流交混不引起質量交換，只引起動量和能量上的交換。考慮湍流交混時的橫向流量，采用以下公式：

(9)

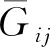
內部通道為：

(10)

(11)

(12)

壁面處通道為：

C1L,Lam=0.413(H/D)-0.5(Ar2/A′2)0.5tanθ

(13)

C1L,Tur=0.73(H/D)-0.5(Ar2/A′2)0.5tanθ

(14)

(15)

其中：

ψb=lg(Reb/RebL)/lg(RebT/RebL)

(16)

(17)

(18)

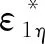
圖3 湍流交混關系式計算的交混系數與實驗結果對比

1.9 對流換熱模型

對于包殼外表面和冷卻劑之間的對流換熱，需要通過努塞爾數(Nu)來確定對流換熱系數。對于LBE，Nu通常被認為是棒徑比和貝克萊數(Pe)的函數。Pacio等[13]在LBE傳熱實驗中選取了3個加熱段測量位置ML1(z/H=1/6)、ML2(z/H=11/6)和ML3(z/H=15/6)，并與液態金屬的對流換熱關系式進行對比，最終推薦Kazimi等[14]關系式用于計算液態鉛鉍的努塞爾數，如式(19)所示。圖4給出經驗關系式與實驗測得努塞爾數之間的對比，可看出關系式低估了ML1處的Nu，這是因為ML1在熱發展區，但在位于充分發展區的ML2和ML3時對Nu的預測比較準確，均方根誤差控制在7.1%。因此程序采用Kazimi等關系式計算努塞爾數，適用范圍為：10≤Pe≤5 000，1.1≤P/D≤1.40。

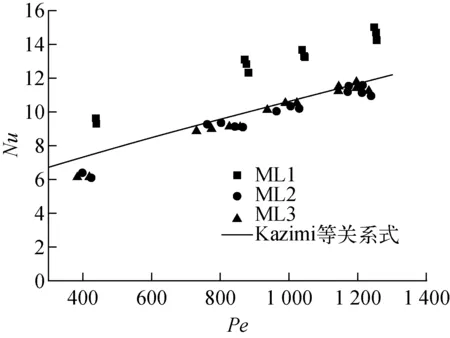
圖4 對流換熱關系式計算的努塞爾數與實驗結果對比

(19)

2 程序驗證

2.1 子通道程序流動驗證

采用CFD可獲得精細的流場數據，為驗證CFD結果可靠，采用大渦模擬計算結果作為基準驗證[15]，該結果為美國阿貢國家實驗室通過開源程序Nek5000計算得到，具有高保真度。本研究在此模型基礎上進一步劃分子通道供程序驗證使用。

棒束結構及子通道編號如圖5所示，繞絲沿流向逆時針方向旋轉。表2列出棒束的具體幾何參數。幾何建模時，由于繞絲與燃料棒之間為線接觸，不利于網格劃分，因此在每個繞絲與燃料棒接觸處做0.25 mm的倒圓角處理，以提高網格質量。

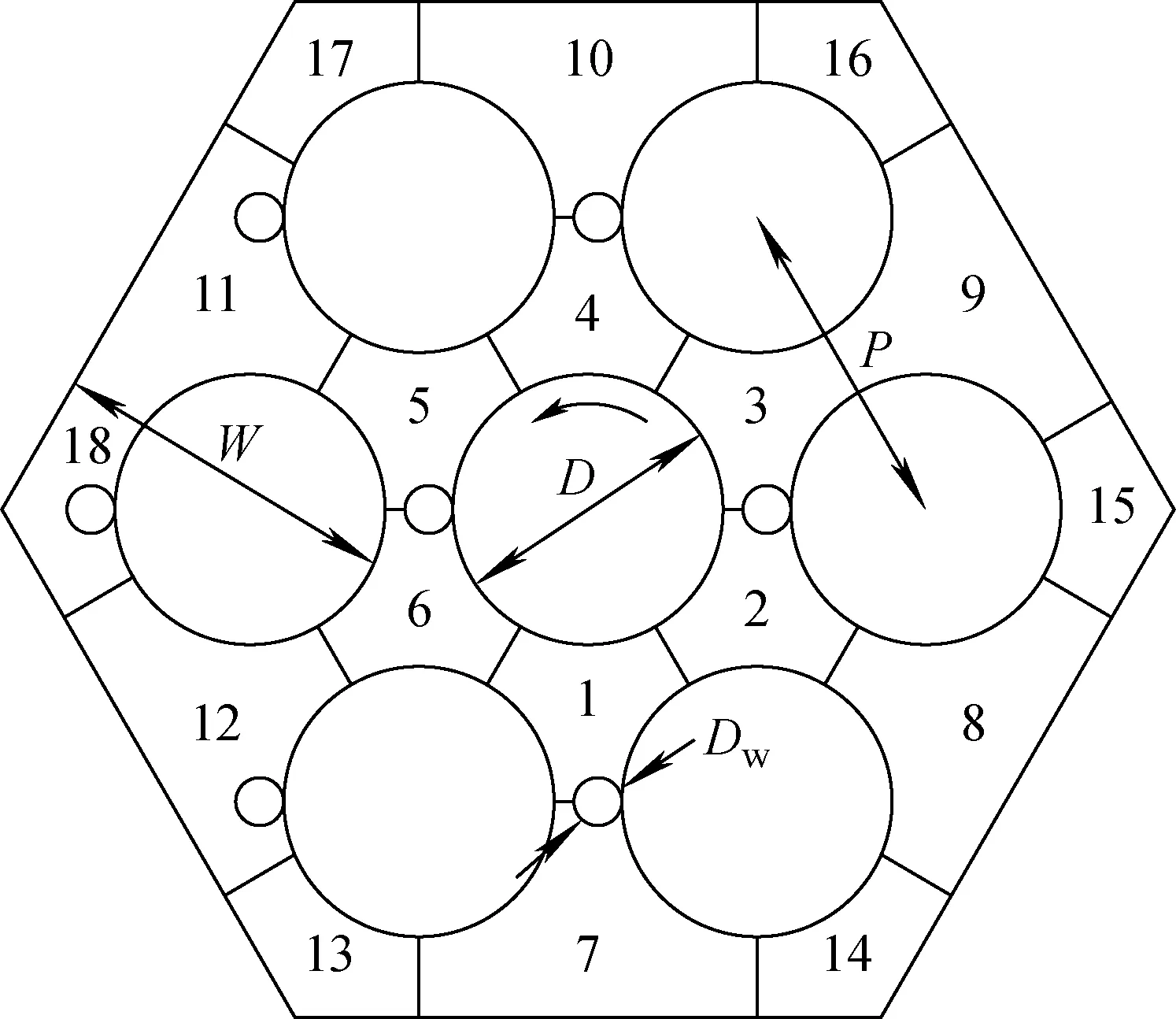
圖5 7棒束子通道編號及劃分

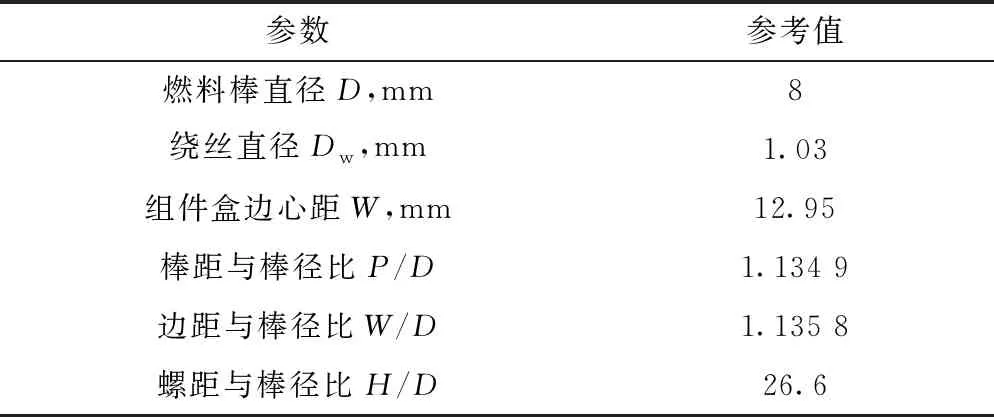
表2 7棒束幾何參數

采用商業計算流體軟件STARCCM+進行多面體網格劃分。圖6示出整體網格及間隙處的局部網格細節。在近壁面處設置4層邊界層網格，選取一個螺距高度進行計算，進出口設置周期性邊界，進口雷諾數為9 457，生成網格后，使用SSTk-ω湍流模型進行計算。

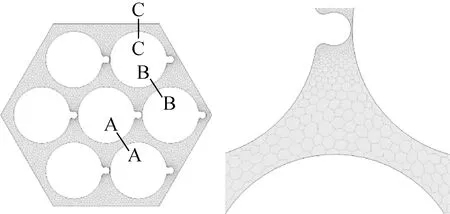
圖6 7棒束網格劃分上視圖

為比較結果，將間隙橫流速度u在整個流向上進行積分，表示為坐標s的函數：

(20)

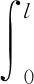
分別選取0.8 mm(網格1)、0.6 mm(網格2)、0.3 mm(網格3)和0.2 mm(網格4) 4套不同尺寸的網格進行無關性驗證。圖7為網格計算結果與LES結果(ANL-LES)在A-A、B-B、C-C間隙處的橫向速度對比。網格3與網格4的結果相近且與LES結果吻合，證明基于大渦模擬流場數據的CFD模擬結果較好，可基于網格3劃分子通道進一步驗證子通道程序。

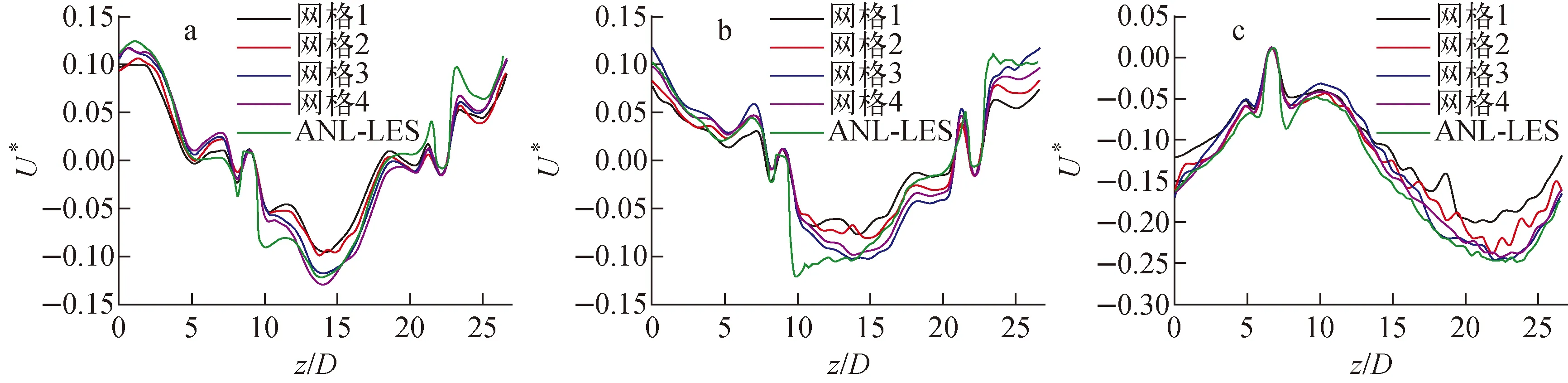
a——間隙A-A；b——間隙B-B；c——間隙C-C

為驗證程序流動計算的準確性，將子通道程序的計算結果與CFD結果進行對比。圖8為出口處不同子通道的質量流量分布，邊通道的出口流量最大，內通道其次，角通道出口流量最小，程序能準確計算出口質量流量。圖9為子通道1的冷卻劑軸向速度沿流向在1個螺距長度的分布，可看出子通道程序計算的軸向速度與CFD計算結果具有相同的趨勢。

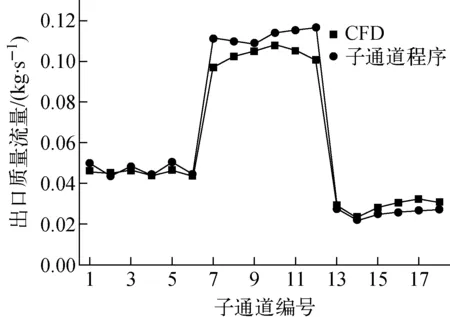
圖8 出口處子通道質量流量分布

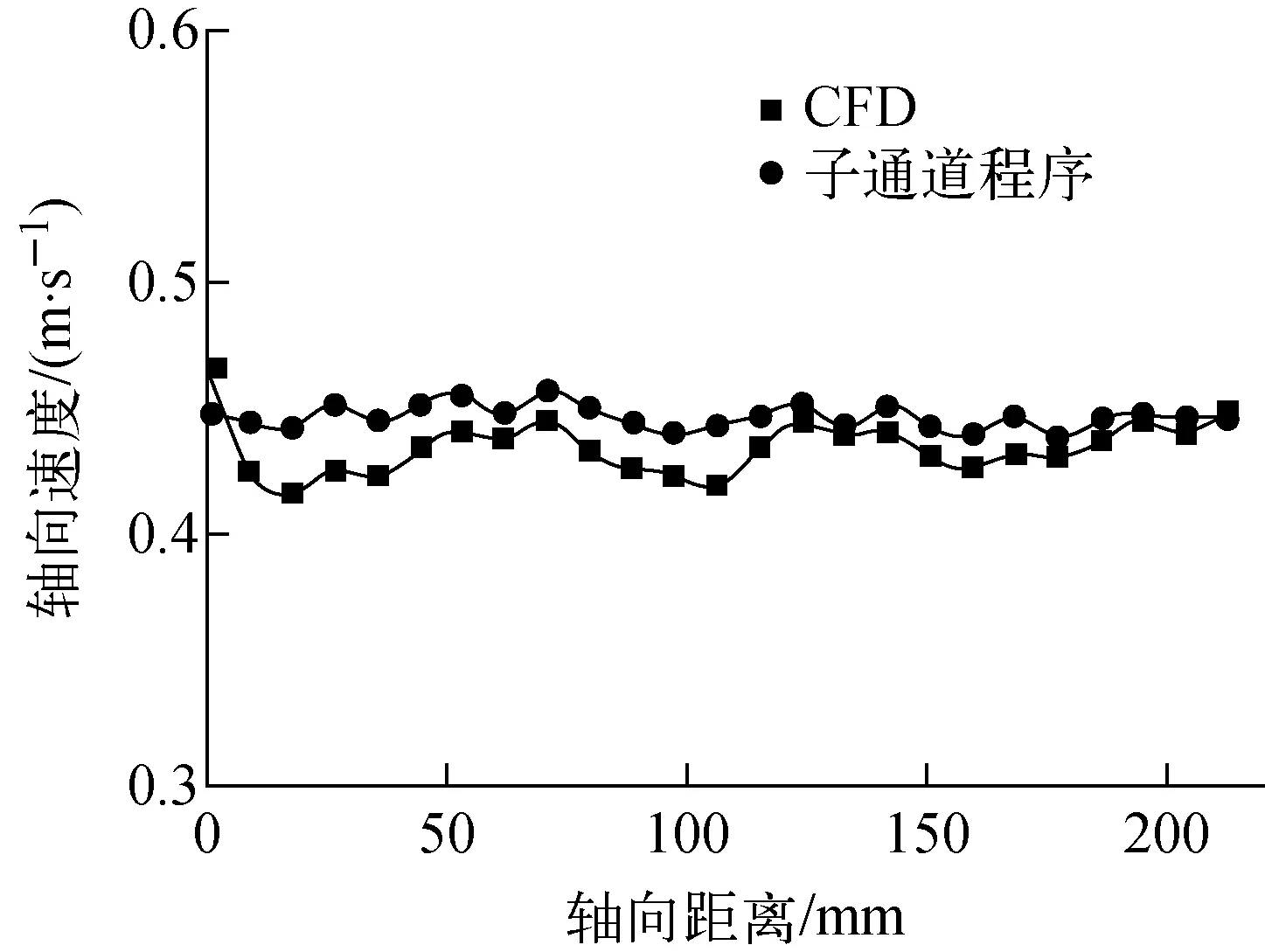
圖9 子通道1軸向速度分布

2.2 子通道程序傳熱驗證

子通道程序要求能準確計算冷卻劑溫度和燃料棒包殼外表面溫度。為驗證程序傳熱計算的準確性，選取Pacio等[13]開展的19棒束含繞絲燃料組件的棒束傳熱實驗進行驗證。燃料組件的具體幾何參數列于表3。具體邊界條件包括進口溫度Tin=473 K、進口質量流量M=19.18 kg/s及總加熱功率Q=197.04 kW，加熱功率均勻分布在每根棒的加熱段上。在程序中模擬824 mm的流動發展段和870 mm的加熱段，棒束子通道劃分與編號方式如圖10所示。

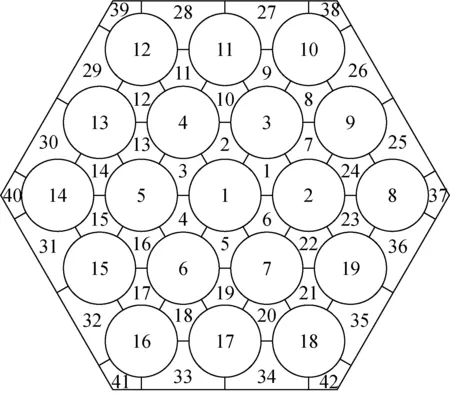
圖10 19棒束的子通道編號和劃分

包殼和冷卻劑溫度計算結果與實驗結果對比如圖11～13所示，分別對應沿加熱段軸向高度的3個不同測量位置ML1、ML2和ML3。其中ML1處于熱發展段，ML2和ML3處于熱平衡段。除實驗數據外，另外選取子通道程序SACOS-PB的計算結果進行對比[16]。由圖12、13可看出，內通道比邊通道和角通道更熱，ML3比ML2的溫度曲線變化更明顯。同一截面上，邊通道和角通道的溫度均低于流體平均溫度。程序計算結果與實驗數據在子通道處的最大相對誤差為4.08%，包殼外表面處的最大相對誤差為4.36%，且與其他子通道程序的計算精度類似，總體計算相對誤差低于5%，驗證結果較好。

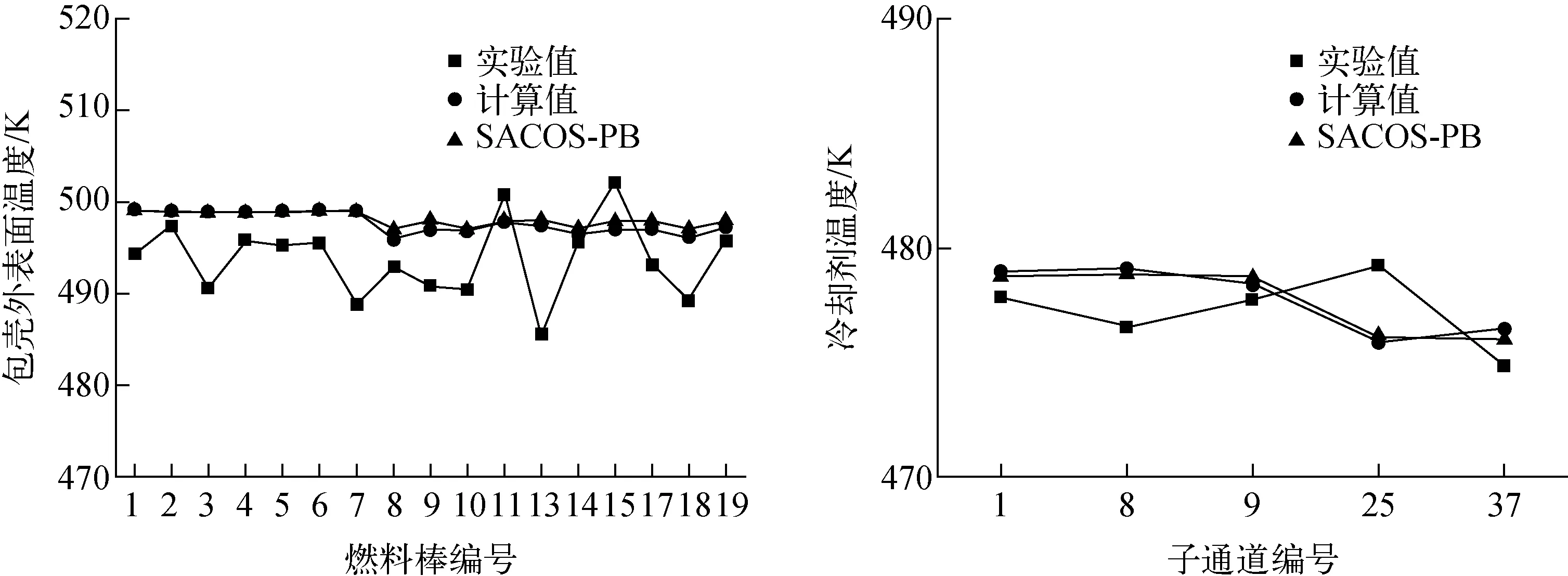
圖11 ML1處包殼外表面和冷卻劑溫度分布

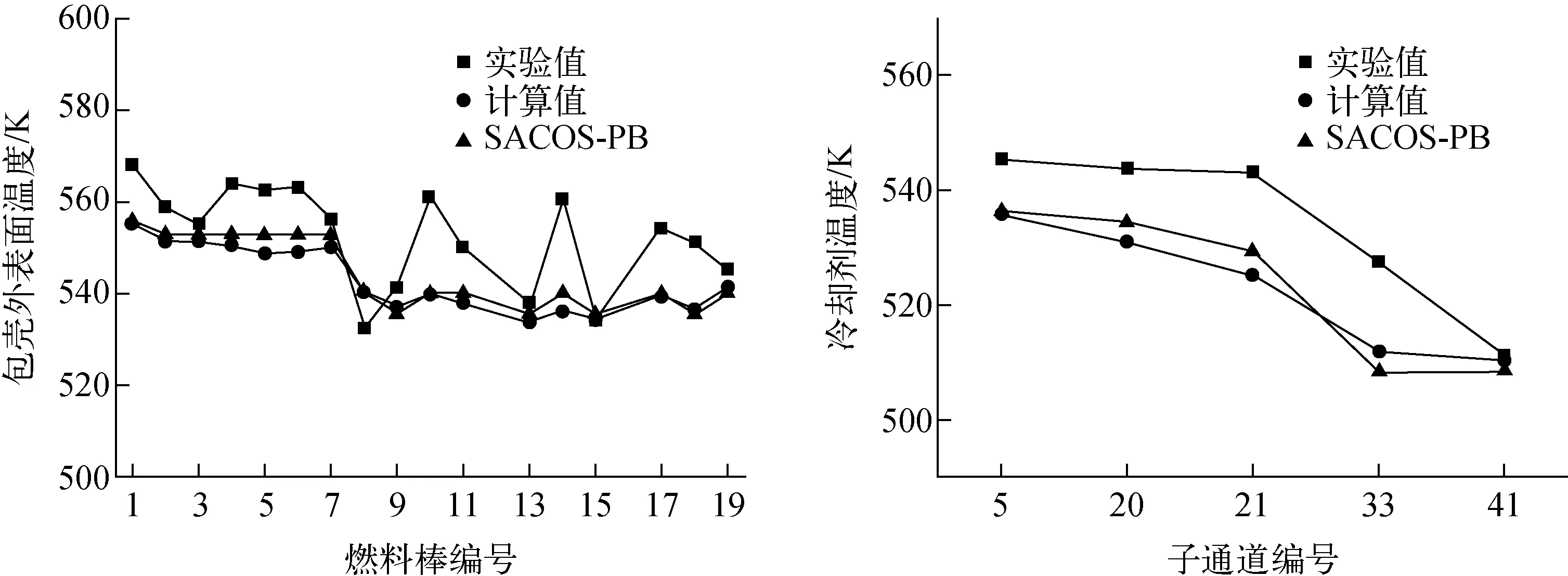
圖12 ML2處包殼外表面和冷卻劑溫度分布

3 結論

本文開發了適用于液態鉛鉍冷卻含繞絲燃料組件的子通道分析程序，并對不同流動和傳熱關系式進行了評價。基于7棒束大渦模擬流場數據驗證了程序流動模塊的有效性，基于19棒束傳熱實驗數據驗證了程序傳熱模塊的有效性。結果表明開發的子通道程序能較好地計算液態鉛鉍冷卻繞絲定位燃料組件的流動傳熱特性，可代替或輔助CFD計算，節約了計算時間。

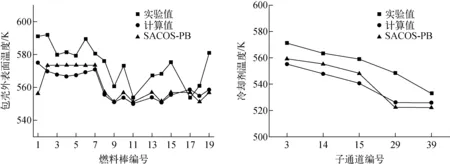
圖13 ML3處包殼外表面和冷卻劑溫度分布