超臨界流體物性畸變特性的多尺度研究

劉旻昀，黃彥平，唐 佳，臧金光，趙學斌，黃善仿，何茂剛，張 博

(1.中國核動力研究設計院 中核核反應堆熱工水力技術重點實驗室，四川 成都 610213；2.清華大學 工程物理系，北京 100084；3. 西安交通大學 熱流科學與工程教育部重點實驗室，陜西 西安 710049；4.大連理工大學 能源與動力學院，遼寧 大連 116024)

超臨界流體的熱物理性質在其臨界點和擬臨界線附近會發生劇烈變化，由于這種獨特的物性畸變特性，萃取和化學合成領域可通過細微的溫度壓力調節使物質的溶解度發生幾個數量級的突變，以達到使分離物析出或控制反應的目的[1]。在超臨界二氧化碳布雷頓循環中，通常將壓縮機進口溫度設置在擬臨界溫度附近，利用密度的畸變特性降低壓縮功、提高系統效率[2-3]。然而，在超臨界水動力循環或超臨界碳氫燃料熱管理系統中，超臨界流體的物性畸變特性還可能誘發傳熱惡化使得壁面過熱失效[4]。因此，為保障和優化超臨界流體在能源動力、傳質萃取、化學反應、環境治理等領域的應用，必須對超臨界流體物性畸變特性進行深入研究。目前，關于物性畸變機理的認識尚未統一。一種觀點[5-7]認為，擬臨界現象與亞臨界氣液相變物性變化特點相近。在擬臨界現象發生時，超臨界流體內部存在類氣結構與類液結構之間的轉變，轉變過程仍可用超臨界氣液共存和擬沸騰來描述。另一種觀點[8-9]將擬臨界現象視作臨界現象的延伸，強調體系內部漲落的影響。第三種觀點[10]則不考慮擬臨界現象本身的特殊性，在研究相關問題時看作物性劇烈變化的單相流體。但上述3種觀點均沒有嚴格的理論支撐，同時也無法給出超臨界流體發生物性畸變的根本原因。

從描述短程相互作用的分子作用力，到描述長程關聯的有序結構，再到宏觀上表現出的均一相態，超臨界流體物性畸變特性存在于微觀、介觀和宏觀的不同尺度上。在微觀尺度上，光散射和中子散射實驗[11]為研究體系的微觀結構變化特點提供了有力手段，而分子動力學[7,12]等模擬手段則作為一種更廉價而精細的補充。在介觀尺度上，對于臨界現象，標度理論[13]和重整化群理論[14-15]從標度不變性出發，用粗粒化的思想建立了完整的理論描述；而對于擬臨界區物性畸變，尚未有理論提出。在宏觀尺度上，關于超臨界流體傳熱異化的研究[16]已有很多，但在擬臨界區物性計算方面，如今應用最為廣泛的NIST數據庫[17]也有較大偏差。針對上述問題，本文從微觀、介觀和宏觀尺度對超臨界流體的物性畸變特性進行全面分析。采用分子動力學模擬復現和研究超臨界二氧化碳在擬臨界區的物性畸變特點；提出一種考慮外場的氣液相變模型，補充擬臨界現象認識上的理論空白，同時結合標度理論，推導部分物性在趨于臨界點時的發散規律；開展高精度的二氧化碳密度、定壓比熱、黏度物性測量實驗，指出現有計算模型的缺陷。

1 分子動力學模擬

本文采用Material Studio軟件中的分子動力學模擬功能，研究二氧化碳流體體系跨越擬臨界點時的微觀結構特性。

1.1 計算模型

力場模型為COMPASS力場[18]，其在單分子或凝聚態物質結構、熱力學性質等方面的預測能力已得到廣泛證實。模擬體系為立方體盒子，在x、y、z方向上均采用周期性邊界條件以消除邊界效應。根據分子數量、截斷半徑無關性、時間步長無關性的檢驗結果，同時盡可能減小計算資源的消耗，設置二氧化碳分子數為256，截斷半徑為1.55×10-9m，時間步長設為7×10-16s。

在模擬過程的前3×10-10s，保持體系的粒子數、體系體積及溫度不變(即正則系綜)，使得體系達到遲豫平衡。此時，模擬結果的統計量收斂到一個準穩態，而與分子的初始排布方式無關。然后，保持體系的粒子數、體系壓力和溫度不變，對體系的密度、雙體分布函數、配位數、靜態結構因子等物理量進行統計。模擬過程中的溫度控制方法為Berendsen控溫法(即恒溫熱浴耦合法)，壓力控制方法為隨機碰撞法。對于分子之間的非鍵相互作用，采用Group-Based加和方法進行求解。另外，還可根據能量波動方法求得定壓比熱，通過統計體系內粒子數目的波動求得等溫壓縮系數等[19]。

1.2 計算結果

圖1為5 MPa下二氧化碳密度的分子動力學模擬結果與NIST數據庫值之間的偏差。可看出，分子動力學模擬能準確預測流體的密度，同時很好地捕捉到該壓力下的氣液相變點，最大相對偏差僅為5.46%。進一步對7.38 MPa和16 MPa下的二氧化碳密度進行了模擬和對比，結果表明：對于遠離臨界點的狀態，分子動力學模擬方法在預測流體密度時精度較高，模擬值與數據庫值的相對偏差小于5%；在臨界點附近計算偏差顯著上升，但仍有相同的變化趨勢。因此，本文所搭建的分子動力學模型可作為定性研究物性畸變現象的手段。

圖1 5 MPa下二氧化碳密度模擬結果與NIST數據庫值的對比

以雙體分布函數g(r)為工具，研究體系的微觀特性。作為分子排列有序性的一種度量，g(r)表示以一個任意指定的粒子為中心，在距離r處找到其他粒子的概率。圖2為7.38 MPa下T=280～350 K的二氧化碳體系的C-C原子雙體分布函數的變化情況，作為對比，圖2中虛線分別為280 K、0.1 MPa下二氧化碳和氦氣的g(r)曲線。從圖2可看出，隨溫度的升高，雙體分布函數的第1峰與第2峰之間的峰谷逐漸升高，說明體系的有序程度不斷減弱、分子排列變得稀疏。當溫度高于310 K后，g(r)曲線中僅存在第1峰，而第1峰之外，與280 K、0.1 MPa下的氣態二氧化碳情形十分相似。這說明體系中僅存在嚴格的近程有序，體系的微觀狀態更接近于氣態。但與氦氣情形下的近程無序且長程無序不同，二氧化碳在氣態條件下仍是近程有序的，這實際上反映了二氧化碳分子不為0的四極矩之間的相互作用。當溫度小于304.13 K或大于305 K時，體系的g(r)曲線基本重合；而在304.13～305 K的溫度區間內，曲線特征發生顯著的轉變。

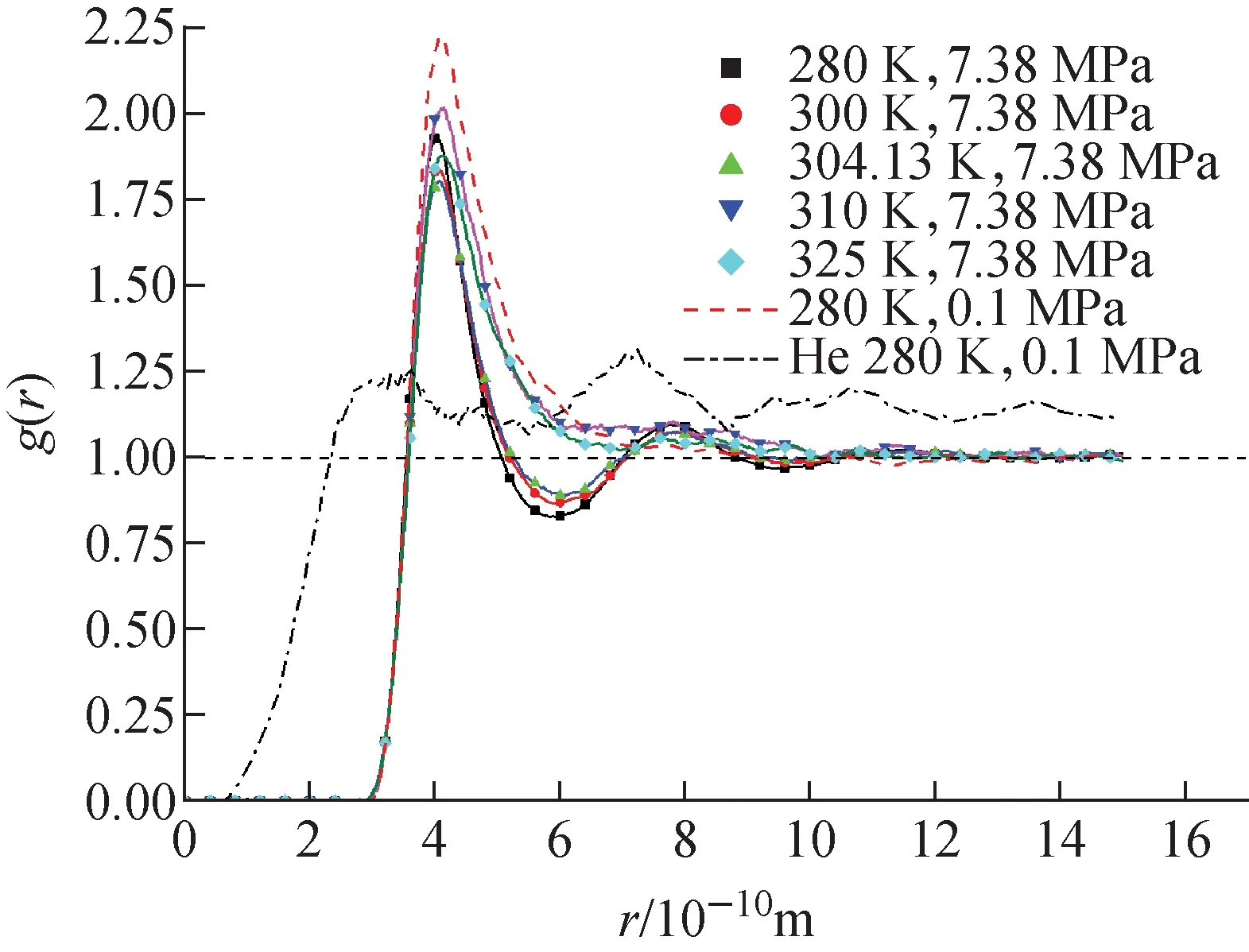
圖2 7.38 MPa下T=280～350 K時C-C原子間雙體分布函數對比

對于一定壓力下的超臨界流體，溫度較低時體系的有序程度較高，表現為近程、中程有序而長程無序，與液體類似；溫度較高時體系表現為近程有序而中長程無序，與氣體相似；在中間的某一狹窄溫度區間內，體系的結構發生劇烈的變化。因此，可進一步將超臨界流體區劃分為類氣區、類液區和擬臨界區，這與散射實驗[11]的測量結果也是吻合的。

2 考慮外場的氣液相變模型

分子動力學模擬從微觀視角上給出了擬臨界現象的直觀認知，但仍無法解釋超臨界流體發生擬臨界現象的原因。為解釋這一問題，本文基于朗道二級相變理論[20-21]和標度理論，提出一種考慮外場的氣液相變模型。

2.1 考慮外場的朗道模型

根據朗道理論在其他體系的推廣形式[22-24]，如描述液晶體系相變的Landau-de Gennes模型[25]，本文提出了一種新模型。在新模型中，序參量η為(ρ-ρc)/ρc，其中ρ為流體的平均溫度，下標c表示臨界點狀態。在這種定義下，η在整個流體域均有明確的定義，且在臨界等容線(ρ=ρc)上等于0。此外，朗道理論中熱力學勢Φ的表達式也按實際流體的特性進行了改進。首先定義一組無量綱變量(p,t,η)，其中p=(P-Pc)/Pc為無量綱壓力，而t=(T-Tc)/Tc為無量綱溫度。新的熱力學勢表達式為：

Φ(p,t,η)=Φ0(p,t)+C(-(p-bt)η+atη2+Bη4)

(1)

式中：a、b、B、C均為大于0的系數，b、C為常數，a、B僅與壓力相關；Φ0(p,t)為與流體溫度和壓力相關的常規項。

相比于經典朗道理論，新模型基于重新定義的序參量η，同時增加了η的一次項。此一次項表示了外場h=p-bt對熱力學勢的作用，也對應于溫度和壓力對于流體狀態的影響。根據朗道理論，一個穩定的熱力學狀態(p,t)對應于(?Φ/?η)p,t=0，由式(1)則有：

h=p-bt=2atη+4Bη3

(2)

因此，對于臨界等容線η=0，流體的壓力與溫度應滿足線性關系(圖3)。無論是對于水、二氧化碳、氮氣還是氧氣，不同流體的臨界等容線均在很大的溫度壓力范圍內保持線性，進而證明了引入的線性外場項的正確性。

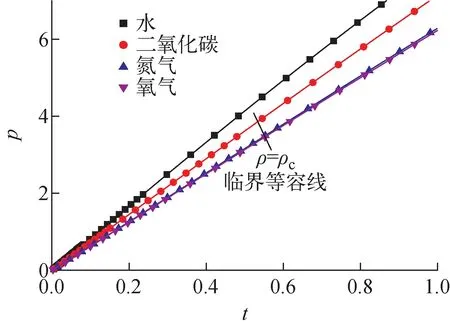
圖3 4種不同流體的臨界等容線

由式(1)的熱力學勢表達式可推導出流體的定壓比熱cp為：

cp=T(?s/?T)P

(3)

(4)

由式(4)可知，定壓比熱cp由常規項cp0和擬臨界增強項兩部分構成。在擬臨界區，密度隨溫度的劇烈變化導致擬臨界增強項的增加。圖4以23 MPa下的超臨界水對式(4)進行了驗證。可看出，在接近臨界密度時，定壓比熱的畸變與?ρ/?T的變化高度相關。

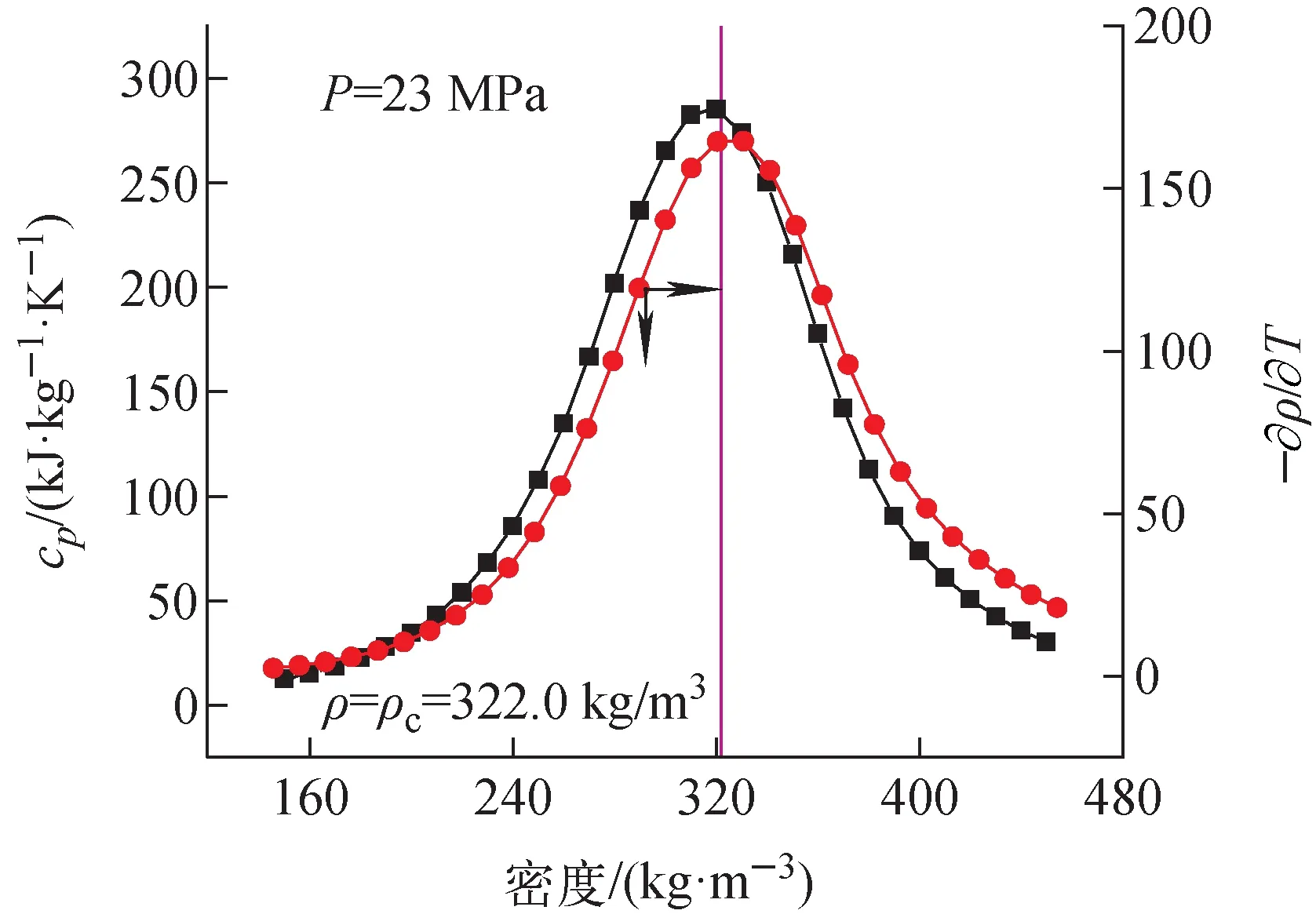
圖4 臨界等容線附近超臨界水的定壓比熱畸變規律

2.2 考慮外場的標度理論

除了可在定量上解釋擬臨界區的物性畸變特性，本文所提出的模型亦適用于亞臨界氣液相變。但對于臨界點鄰域，模型的預測值與實驗測量值存在顯著的偏差。以臨界等溫線和臨界等壓線為例，則：

(5)

對應的臨界指數δ=3與實驗測量的結果δ=4.8±0.02不相符。針對此問題，標度理論和重整化群理論的結論為：在臨界點附近，體系內部漲落的影響不可忽略，導致忽略了漲落的朗道理論不再適用。此時不能遵循平均場近似，需考慮體系內部劇烈漲落對熱力學勢的影響，因此有必要對模型在臨界點鄰域進行修正。根據標度理論，趨于臨界點時體系的關聯長度發散，此時系統具有標度不變性，熱力學函數可轉換為系統參數的廣義齊次函數f。對于外場影響下的序參量，則：

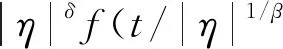
(6)

式中：±分別對應η>0和η<0；β為熱膨脹系數。

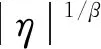
(7)

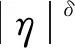
3 超臨界二氧化碳高精度物性測量實驗

在宏觀尺度上，目前超臨界二氧化碳擬臨界區熱物理性質實驗數據稀少，且不同來源實驗數據間的一致性也較差。因此，本文聯合西安交通大學和大連理工大學開展了兩組“背靠背“的物性測量實驗進行驗證。以二氧化碳為實驗工質，分別采用U型管振蕩法[26]、流動型量熱法[27-28]、毛細管法[29]，完成25～500 ℃溫度范圍、7～14 MPa壓力范圍內的密度、定壓比熱和黏度的測量，共得到數據點1 940個，圖5為實驗裝置示意圖。表1列出在置信因子k=2、置信度為95%的條件下兩組實驗中壓力、溫度、定壓比熱及黏度的測量不確定度。

表1 物性測量實驗的不確定度

a——定壓比熱實驗測量系統；b——黏度和密度實驗測量系統

從“背靠背”驗證的角度來看，在相同工況下，兩組密度測量結果的平均相對偏差僅為0.127%，吻合較好。將實驗結果與當前應用最為廣泛的Span-Wagner方程[30]和Vesovic黏度計算模型[31]的計算結果進行對比，對于物性變化較為平緩的一般區域，實驗結果與計算結果的偏差很小(表2)。但對于物性劇烈變化的擬臨界區，實驗結果與計算結果的偏差顯著增大，且表現出物性畸變越劇烈則偏差越大的趨勢(表3)。現有的擬臨界區數據點仍較少，數據點壓力偏高且溫度間隔過大，實驗精度需進一步評估和優化。

表2 一般區域內實驗測量結果與計算結果的相對偏差

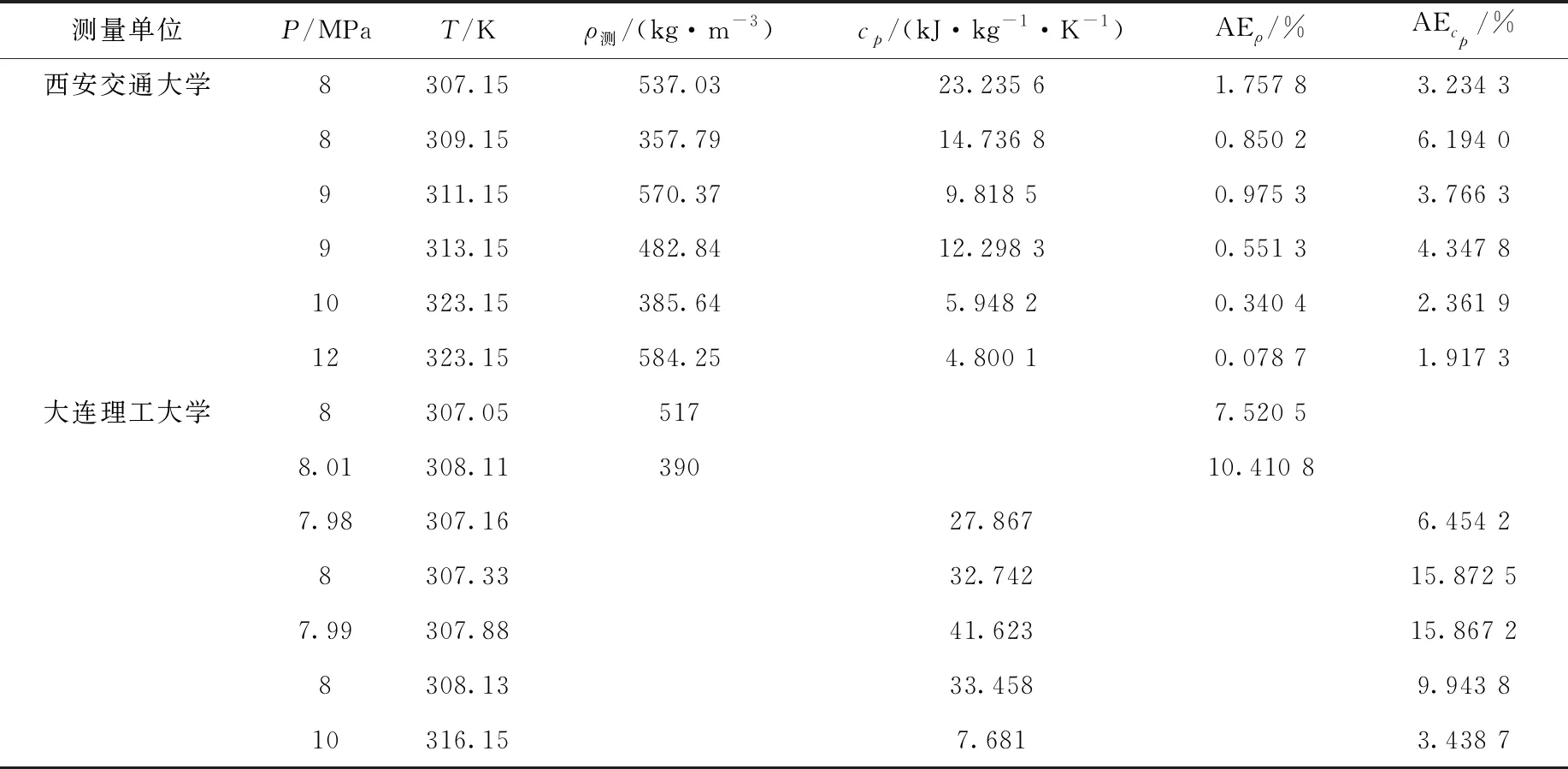
表3 擬臨界區部分實驗測量結果與計算結果的偏差

現有的二氧化碳熱物理性質理論模型在擬臨界區之外計算精度較好，但在近臨界區仍存在缺陷，計算精度需實驗驗證并進一步提高。對于超臨界二氧化碳布雷頓循環，為了獲得更高的系統效率，往往需要盡可能將背壓設置得低(如7.4 MPa)，利用這種畸變特性來減小壓縮功。因此，掌握二氧化碳熱物性在近/超臨界區域精確的實驗數據及其變化規律是一個關鍵問題，需要在實驗技術、理論模型等方面進一步研究。

4 超臨界流體區的嚴格劃分

通過微觀、介觀、宏觀3個不同尺度的研究分析，得到超臨界流體發生物性畸變的機理。分子動力學模擬的結果表明，超臨界流體在擬臨界區發生物性畸變時，同時伴隨類氣-類液結構之間的轉變，而在漲落主導的臨界點鄰域內，流體分子之間存在長程關聯。長程關聯帶來的體系自相似性為采用粗粒化方法建立標度理論提供了依據，但也導致傳統連續體假設的失效。因此，研究處于臨界點鄰域的流體必須從更為基礎的假設出發，采用分子動力學模擬或格子玻爾茲曼方法[32]。隨著遠離臨界點，漲落迅速衰減以至于可忽略，此時基于平均場思想的朗道理論變得適用。同時由于不存在長程關聯，傳統的宏觀描述(如Navier-Stokes方程)同樣成立，但需注意物性畸變對于流動、傳熱等宏觀行為的影響。因此，超臨界流體區域可進一步劃分為4個子區域(圖6)：臨界點鄰域、類氣區、類液區和擬臨界區。

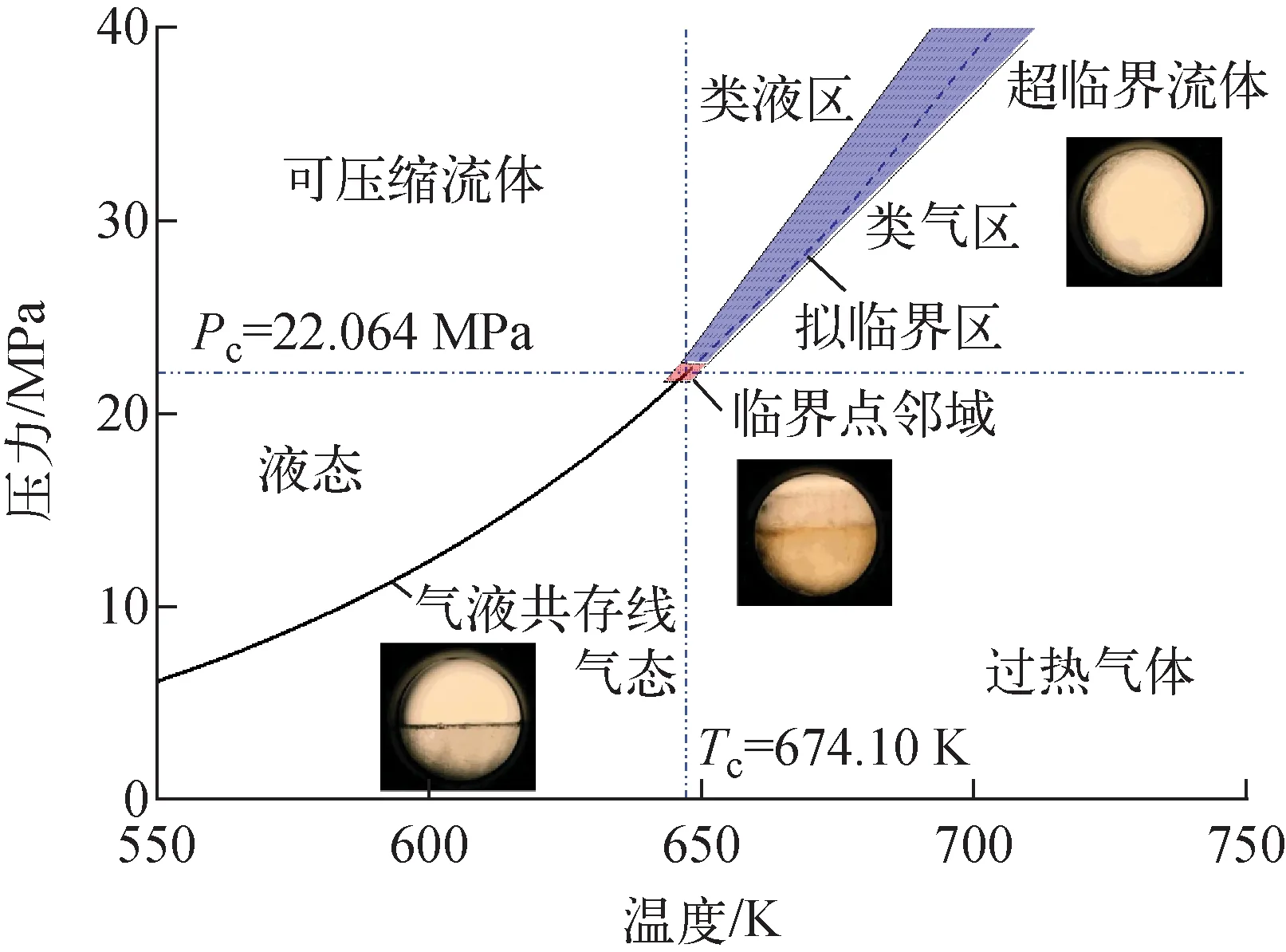
圖6 臨界等容線附近超臨界水的定壓比熱畸變規律

關于各區域的劃分，首先可估算臨界點鄰域的范圍。當沿臨界等容線趨近臨界點時，關聯長度ξ的發散遵循[33]：

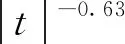
(8)

當|t|足夠大時，流體分子之間無長程關聯，而只有分子間作用力決定的短程關聯，因此ξ≈ξ0≈10-10m。只有當t≈10-6時，關聯長度才會增長到與流體層厚度相當的μm量級。對于二氧化碳，t≈10-6對應于T-Tc≈3×10-4K。因此，臨界點鄰域的范圍是很小的。對于大部分的超臨界流體應用場景而言，傳統的宏觀描述均適用。對于其他3個區域，Banuti[34]推廣了亞臨界條件下的克拉伯龍方程，得到關于超臨界流體的劃分方法；Kurganov等[35]則從流體壓縮性的評估出發，以相對膨脹功Eq=pβ/ρcp作為劃分依據。總地來說，擬臨界區的劃分更多是經驗性的，因此兩種劃分方法都可行。在實際工程中，為了使用方便，也可根據第2節中的結論，以無量綱密度作為劃分擬臨界區的簡單判據。

5 結論

本文通過微觀、介觀和宏觀3個不同尺度的分析論證，發現了導致超臨界流體物性畸變的不同機制。根據影響機制的不同，在相圖上，超臨界流體區可進一步細分為臨界點鄰域、擬臨界區、類氣區和類液區，得到如下結論：1) 分子動力學模擬的結果表明，在跨越擬臨界線時，超臨界流體的微觀構型會發生類氣-類液之間的轉變；2) 在臨界點鄰域內，體系的熱力學函數、漲落和關聯長度趨于臨界點時按冪律發散，此時考慮外場的標度理論可很好地描述，但傳統的宏觀描述和平均場理論均失效；3) 臨界點鄰域的范圍很小，以無量綱溫度t=(T-Tc)/Tc表示時，近似滿足t<10-6；4) 對于絕大部分工程應用場景，超臨界流體內部的漲落影響均可忽略，此時考慮外場的氣液相變模型能很好地描述物性畸變的規律；5) 無量綱密度|η|<0.25可作為劃分擬臨界區的簡單判據，對于二氧化碳，對應密度為350～585 kg/m3；6) 超臨界二氧化碳的物性測量實驗結果表明，現有的物性模型在描述擬臨界區物性畸變特性方面仍有不足，但對于擬臨界區之外的一般區域已有足夠高的計算精度。