優化GA-BP神經網絡模型及基坑變形預測

劉 錦， 李峰輝， 劉秀秀

(1. 陜西鐵路工程職業技術學院城軌工程學院， 陜西 渭南 714000；2. 鄭州市交通規劃勘察設計研究院， 河南 鄭州 450000； 3. 曲阜遠東職業技術學院， 山東 濟寧 273100)

0 引言

基坑工程影響因素多、施工難度大，工程建設風險隨開挖規模擴大急劇增加[1]。坑內土體因開挖卸荷形成內外壓力差，支護結構內力改變產生位移形變；若結構強度或剛度不足，易導致支護樁傾斜，發生土體坍塌事故，嚴重時會造成地坪開裂、管線損壞及周圍建筑物不均勻沉降[2]。因此，對基坑開挖實施動態監測尤為重要。根據監測數據適時調整施工工藝和支護參數，可實現信息化施工，保證基坑盡可能在安全經濟的環境下進行施工。

傳統基坑監測方法忽視位移形變的預警，僅事后采取補救措施，錯失加固修復最佳時機，存在重大安全隱患。基坑變形隨時間呈不規則非線性演化，位移值屬于非平穩的復雜時間序列，因而具有優越的非線性動態處理能力的BP(back propagation，簡稱BP)神經網絡被廣泛用于基坑變形預測。目前，許多學者依托實際工程構建多種BP神經網絡模型用于基坑變形預測。張慶華等[3]提出“新陳代謝”方法選取人工神經網絡模型訓練樣本，能有效預測基坑的長期變形； 楊茜[4]通過對比優選網絡訓練模式和傳遞函數，改進模型對隧道結構整體沉降預測效果良好； 胡啟晨等[5]建立BP神經網絡預測模型用于基坑開挖變形預測，具有一定應用價值； 譚儒蛟等[6]基于神經網絡提出一種土體參數反演方法； 劉聰等[7]從基坑變形影響因素分析輸入層神經元結構，并結合工程實例進行預測分析。

BP算法因自身傳遞函數限制，導致其存在收斂速度慢、易陷入局部極小點的缺陷，引入具有強大的全局尋優能力的遺傳算法可在一定程度上有效克服其不足。利用遺傳算法隨機性和全局性特點，李彥杰等[8]基于遺傳算法對BP算法的初始權重和閾值進行改進，建立的預測程序對深基坑地下連續墻圍護結構水平位移預測準確度高； 周星勇等[9]針對BP神經網絡存在的過度擬合和局部最優的缺點，引入自適應增強算法對遺傳神經網絡預測模型進行改進； 胡圣武[10]用遺傳算法對灰色神經網絡進行改進，提高了預測精度； 宋楚平[11]利用遺傳算法對模型權重初值進行優選，改進模型的收斂速度和泛化能力均得到提升。

上述預測模型對基坑變形具有一定參考價值，但在訓練樣本選取、樣本數據預處理及隱含層結構設計等方面仍存在優化空間，模型的預測精度和運算速度有待進一步提高。為解決上述問題，本文對GA-BP模型的歸一化區間和隱含層結構進行深入優化，并對實際工程基坑支護樁體測斜位移展開預測，通過誤差分析驗證預測模型的合理性和優化效果，以期進一步為基坑變形監測提供理論依據。

1 GA-BP神經網絡

1.1 BP神經網絡

BP神經網絡理論以人腦的自組織、自適應及容錯性為模擬對象，通過BP算法對實測資料進行自身訓練和規則學習，高效解決有關問題。模型由輸入層、隱含層及輸出層構成，各層可根據需要擴展成多層，鄰近層以權重和閾值連接并借助傳遞函數承擔信號的轉化與傳播任務，屬于多層前饋性神經網絡，網絡拓撲結構如圖1所示。圖中：x1，x2，…，xi-1，xi表示初始輸入數據；w1，w2，…，wi-1，wi和α1，α2，…，αi-1，αi分別表示輸入層權值和閾值；γ1，γ2，…，γj-1，γj和β1，β2，…，βj-1，βj分別表示隱含層權值和閾值；i和G分別表示輸入值和輸出值。

圖1 BP神經網絡模型拓撲結構圖

BP神經網絡獨特的無監督學習算法是實現其功能的核心，利用梯度下降法校正輸出結果誤差平方和的誤差反向傳輸，是保證預測結果精度的前提。學習算法流程主要由信號順向傳播、誤差反向傳輸及循環訓練與判別收斂等3個階段構成。

1.2 遺傳算法優化流程

遺傳算法(genetic algorithm，簡稱GA)是一種結合Darwin適者生存進化論和Mendel基因遺傳機制形成的具備全局最優搜索能力的算法，目的在于實現BP神經網絡各層連接權值和閾值的最優化，擺脫BP算法對梯度信息的過度依賴。

GA算法優化基本思路是： 將初始權重和閾值編碼完成種群初始化，確定個體篩選標準—適應度，利用遺傳算法的選擇、交叉及變異操作對群體進行淘汰選優，最終獲得神經網絡最佳連接權值和閾值，其詳細算法流程如圖2所示。

圖2 GA-BP神經網絡模型算法流程圖

2 GA-BP神經網絡預測模型優化

2.1 樣本數據預處理方法的優化

神經網絡訓練需對實測數據進行歸一化處理，即將原始數據映射至選定的歸一化區間，據此可將有量綱的原始數據轉變成純數值的標量，在提高模型訓練速度和靈敏度的同時，有效預防陷入S型傳遞函數的飽和區。因此，歸一化區間的范圍對于神經網絡模型的性能具有重要影響。

為尋求GA-BP神經網絡模型的最佳歸一化區間，利用MATLAB神經網絡工具箱中的Postreg函數，對采取不同歸一化區間進行歸一化處理的模型開展訓練效果回歸分析驗證，以相關參數R(即網絡輸出與目標輸出的相關系數)表征各歸一化區間的訓練質量，其中R值越接近于1，表明網絡輸出與目標輸出越接近，網絡的性能越好，具體分析結果如圖3所示。由圖可知，采用不同歸一化區間網絡模型的訓練效果離散性較大，最佳歸一化區間為[0.05, 0.95]。

2.2 隱含層結構優化

神經網絡模型輸入層和輸出層結構由預測對象的訓練樣本和需求結果共同決定，因而中間隱含層的構成及其含有的神經元節點數將直接影響模型的學習能力和運算處理水平。需要注意的是，節點過少會造成模型容錯性差，導致識別訓練樣本的能力降低，而節點過多則引起學習算法的運行時間顯著增長，降低實際工程應用價值。因此，模型的隱含層結構需根據具體情況適當調整。

注： 橫坐標值表示歸一化區間左端點，x表示歸一化區間左端點值。

2.2.1 單隱含層及神經元個數

現有神經網絡預測模型多采用單隱含層結構，參考相關工程實例[3-9,11-15]，隱含層神經元個數與輸入層神經元個數的關系如圖4所示。

圖4 隱含層神經元個數與輸入層神經元個數關系

利用最小二乘法對上述數據進行曲線擬合，可得單隱含層最佳神經元個數與輸入神經元個數的關系，可見單隱含層節點數最佳區間為[4，7]，單隱含層能夠包含的節點數受模型自身限制，顯然無法滿足輸入神經元個數較多的工況。

2.2.2 雙隱含層及神經元個數

采用實測數據作為訓練樣本代入預測模型，即輸入神經元個數較多時，單隱含層結構由于包含的神經元個數過多，將顯著降低網絡訓練效果和模型預測精度。

參考相關方法[4]和數據[13]分別開展GA-BP神經網絡的單、雙隱含層訓練，訓練效果如圖5所示。

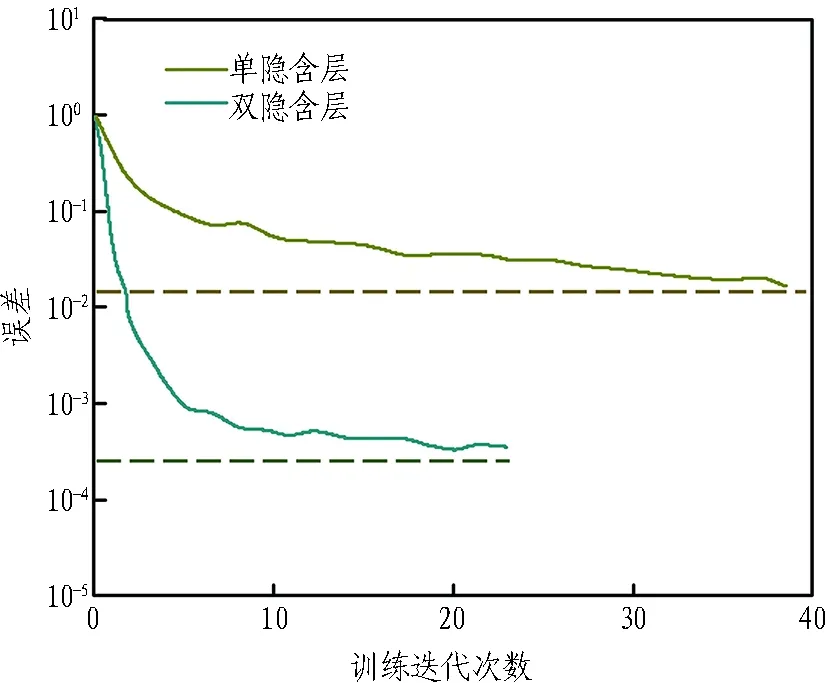
圖5 單、雙隱含層訓練效果圖

由圖5可知，雙隱含層結構達到預期目標誤差的循環迭代次數均小于單隱層結構，說明當輸入層節點數較多時，采用雙隱含層結構的神經網絡模型的訓練效果遠比單隱含層結構的好。

部分訓練程序代碼如下：

[Pn,minp,maxp,Tn,mint,maxt]=premnmx(P,T);

[kn,ks]=mapminmax(k);

[fn,fs]=mapminmax(f);

p=Pn;t=Tn;

net=newff(minmax(P),[a,b],{‘tansig’,‘purelin’});

net.trainParam.show=x1;

net.trainParam.epochs=x2;

net.trainParam.goal=x3;

net.trainParam.lr=x4;

[net,tr]=train(net,Pn,Tn);p,t。

其中，P和T是樣本歸一化后訓練樣本的輸入和輸出，[a,b]、x1、x2、x3、x4均為適時調整參數。

3 改進模型的建立

3.1 輸入層與輸出層設計

基坑施工環境是動態變化的，因此，沉降變形具有“時空效應”，運用前期實測數據預測下一階段變形情況，可顯著降低人為因素干擾和施工環境差異引起的誤差。本文用連續4次的變形數據預測第5次位移值，故輸入層神經元共4個，輸出層表示該測點4+id的沉降參數，即含有1個神經元。

3.2 隱含層

輸入神經元個數大于4時，采用雙隱含層結構可有效防止函數溢出，提高模型預測結果的速度和精度，且可根據需要實時增加樣本數據，實現基坑變形的實時動態監測。經試算確定隱含層的神經元個數分別為7、8，因此，本文GA-BP預測模型的網絡結構為“4—2(7，8)—1”。

3.3 訓練樣本選取與數據預處理

部分學者以基坑變形影響因素作為訓練樣本[11,14]，但由于各因素間關系錯綜復雜，難以準確把握最關鍵因素，且部分指標無法量化，導致建立的模型與實際情況匹配度低，預測結果與期望值相比誤差過大。因此，本文采用基坑變形實測數據作為模型輸入量，在有效降低人為因素干擾的同時能夠顯著降低施工環境差異引起的誤差，從而較好地反映系統的內在變形規律，預測結果可以更好地應用于工程實踐。同時，鑒于施工初始階段監測數據少，無法滿足樣本需求，通過“新陳代謝”的方式控制訓練樣本，將施工期間的監測數據實時添加至樣本中，在提高模型預測精度的同時實現動態監控。

將選取的訓練樣本進一步歸一化預處理至[0.05, 0.95]，計算過程如式(1)所示。

(1)

歸一化與反歸一化MATLAB實現程序語言如下：

輸入訓練樣本p和訓練輸出樣本t

fori= 1:n；

P(i,:)=0.9*(p(i, :)-min(p(i, :)))/(max(p(i, :))-min(p(i, :)))+0.05；

T(i,:)=0.9*(t(i, :)-min(t(i, :)))/(max(t(i, :))-min(t(i, :)))+0.05。

最后，MATLAB軟件要將訓練樣本的輸出值和預測樣本的輸出值都進行反歸一化：

y=(Y(1,:)-0.05)*(max(t)-min(t)/0.9+min(t)；

yt=(Yt-0.05)*(max(t)-min(t))/0.9+min(t)。

其中，Y為訓練樣本輸出值，Yt為預測樣本輸出值。

4 工程實例預測

4.1 工程概況

某人防工程擬建場地鄰近交通要道及市政排污管道密集區域，北側15 m為地下車庫工程基坑，西北側為重要歷史建筑保護范圍。基坑平面呈不規則多邊形，總面積約22 000 m2，挖土深度為7.70～11.60 m，基坑上部4.0 m采用土釘支護，下部為樁錨支護，基坑周邊采用高壓旋注漿形成的水泥墻作為止水帷幕，安全等級為一級。西側有臨時道路，在地面1.2 m以下采用樁錨支護，上部1.2 m在冠梁上砌筑磚墻作為支護結構。在基坑周邊共布設8個測斜管，選取CX-6號測斜管的監測數據進行支護樁位移預測。對基坑變形安全進行監測，可及時掌握支護結構受力和變位情況，保證項目施工處于安全經濟的狀況下運行，基坑平面及測斜管布置如圖6所示。

圖6 基坑平面及測斜管布置示意圖

4.2 模型優化效果驗證

為驗證GA-BP模型優化效果，將優化GA-BP神經網絡的預測結果與未改進的BP和GA-BP神經網絡模型進行對比分析，通過相對誤差表征預測效果優劣，結果如圖7所示。

圖7 模型預測效果對比

由圖7可知， 優化GA-BP神經網絡模型的殘差值及其波動性明顯優于常規BP模型和未經優化處理的GA-BP模型，進一步驗證了本文模型具有更好的預測精度和可靠性。

4.3 模型合理性驗證及誤差分析

CX-6測斜管不同深度處的水平位移隨時間的變化曲線如圖8所示。由圖可以看出，位移整體隨時間增長呈3階段變化，即快速增長階段Ⅰ、穩定發育階段Ⅱ、緩慢變形階段Ⅲ； 變形幅度與測斜深度呈反比； 測斜變形增長速率逐漸趨于緩和，在50 d之后基本保持穩定。

圖8 CX-6測斜管不同深度處的水平位移隨時間的變化曲線

經過反復試運行確定單隱層最佳神經元個數區間為[4，7]，此時模型循環收斂速度快，運行誤差小，預測精度高。

選取時間0 ～ 40 d共40組數據作為訓練樣本，迭代計算達到預期設定誤差后，對41～50 d對應CX-6測斜管不同深度(2.0～4.5 m)的水平位移進行預測，其實測與預測結果對比如圖9所示。

由圖9可知，預測曲線與實測值相比吻合度高，由于基坑開挖過程中施工環境動態變化且次要影響因素被忽略，導致預測值普遍略小于實測值； 同時，變形趨勢具有時間記憶特性，模型對時間點接近訓練樣本的位移預測值精度更高，二者差值隨時間增長逐漸變大。因此，實際應用時需要不斷更新訓練樣本以提高長期預測的精度和可信度，工程實踐中可據此掌握基坑不同深度的變形情況，相應采取不同的加固預防措施，有效防止工程事故的發生，實現信息化動態施工監測。

通過精度評價指標(絕對誤差區間寬窄、相對誤差分布狀態)對預測值進行誤差分析，評判預測效果，不同深度下的水平位移誤差情況如圖10所示。

由圖10可以看出，整體上各深度的位移預測值偏差均保持在0.2 mm以內，絕對誤差區間寬度為0.07 mm； 最大相對誤差為4.0 m深度處的1.35%，顯然滿足施工安全要求，能夠為工程施工提供準確的參考依據。

(a) 2.0 m深度 (b) 2.5 m深度 (c) 3.0 m深度

(d) 3.5 m深度 (e) 4.0 m深度 (f) 5.0 m深度

圖10 不同深度下的水平位移預測誤差分布

5 結論與建議

針對現有GA-BP神經網絡預測模型在訓練樣本預處理和隱含層結構設計方面的不足，提出進一步優化方法，主要結論如下：

1)基坑變形隨時間呈不規則非線性演化，具有強大全局尋優能力的遺傳算法可有效克服BP算法收斂速度慢、易陷入局部極小點的缺陷，顯著提高神經網絡模型的收斂速度和泛化能力。

2)基坑變形“時空效應”顯著，通過“新陳代謝”方式選取訓練樣本可顯著降低人為因素干擾，相關系數回歸分析驗證樣本預處理的最佳歸一化區間為[0.05, 0.95]；單隱含層的最佳神經元個數區間為[4，7]，雙隱含層結構適用于輸入神經元個數較多情況，可根據需要實時添加監測數據，防止函數溢出，有助于提高預測結果的速度和精度。

3)基坑測斜管位移隨時間增長呈快速增長、穩定發育、緩慢變形等3階段變化，變形趨勢具有時間記憶性； 精度評價指標符合安全施工需要，可實現動態化施工監測，經多模型對比可知模型優化效果良好。

目前僅對GA-BP神經網絡模型進行雙隱含層結構設計，后續能否采用三或四隱含層結構有待進一步研究，以提高神經網絡模型的運算速度和預測精度。