基于極限分析的復合地層淺埋隧道掌子面上限支護壓力研究

陳登開， 鐘久強， 余志勇， 蔣亞龍, *， 朱碧堂

(1. 南昌軌道交通集團有限公司, 江西 南昌 330038； 2. 華東交通大學 江西省巖土工程基礎設施安全與控制重點實驗室, 江西 南昌 330013； 3. 江西省地下空間技術開發工程研究中心, 江西 南昌 330013)

0 引言

自我國交通強國戰略實施以來，以地鐵為代表的城市軌道交通建設穩步推進。截至2020年底，我國城市軌道交通營運里程已近8 000 km，其中地鐵里程超7 100 km[1]。地鐵隧道建設過程中，經常遇到掌子面存在多種土質、軟硬不均的復合地層。不同地層中掌子面支護壓力大小差異懸殊，例如： 黏聚力很強的泥巖中可采用敞開式掘進，土艙無需加壓，而在松散的砂土中掘進時往往需要滿艙推進[2]。不同復合程度的土體使得掌子面所需支護壓力更加難以確定，且地鐵沿線通常為城市核心地段，周邊環境復雜，其對臨近地層的允許變形要求也更為嚴格。支護壓力過大易導致地表隆起破壞，過小易引發掌子面主動失穩，均易誘發土體沉降和鄰近地埋管線或建(構)筑物的開裂破壞，造成工程事故。因此，明確不同地層復合程度下，盾構施工時合理的掌子面支護壓力與失穩規律，對指導盾構隧道安全施工具有重要意義。

針對均質地層盾構隧道掌子面極限支護壓力及其失穩模式，國內外許多學者已展開了大量原位和模型試驗研究。文獻[3]利用氣囊模擬無襯砌隧道，探究了砂土地層中不同埋深下隧道極限支護壓力，指出密實砂土中掌子面穩定性與埋深無關。Chambon等[4]基于離心試驗，開展了均質砂土中不同隧道埋深、土體重度及隧道直徑下掌子面極限支護壓力及破壞模式研究，結果表明支護力及失穩模式主要受隧道直徑控制。Kamata等[5]通過小型模型箱試驗，研究了砂土地層加固對掌子面穩定性的影響，得到延伸至地表的倉筒狀失穩面。湯旅軍[6]通過室內模型試驗發現干砂地層中深埋隧道極限支護力趨于穩定，飽和砂土中失穩面為楔形與棱柱組合體。

原位測試和室內模型試驗大多探究均質砂土地層中掌子面極限支護力下限解，不能考慮復雜土層和邊界條件。隨著有限元、離散元軟件和計算機技術的發展，數值模擬分析成了分析隧道掌子面穩定的重要工具。Vermeer等[7]通過大量有限元分析擬合得到了不排水條件下掌子面極限支護壓力下限解簡化計算公式。王林等[8]利用有限元和理論分析提出了一種考慮局部失穩的盾構隧道掌子面被動破壞機制。王俊[2]利用PFC3D顆粒流程序揭示了上軟下硬地層中不同硬巖占比條件下的深埋隧道砂土超挖機制。

總的來看，現有研究主要針對均質土層中掌子面支護壓力不足導致的主動失穩破壞，未考慮復合地層中由于不同巖土體復合程度導致的掌子面失穩模式與其在均質土層的區別，且對支護壓力過大導致掌子面土體發生被動破壞對應的上限解及破壞模式也鮮有涉及[9-10]。鑒于此，本文針對南昌地區典型上覆砂-下臥泥巖復合地層盾構隧道開挖斷面，采用三維有限單元極限分析軟件Optum G3，探究不同泥巖占比下掌子面極限支護力上限解與失穩模式，并進一步分析埋深比C/D、內摩擦角φ及黏聚力c對上限支護力的影響。

1 南昌地區典型地質條件

王凌等[11]根據南昌地鐵1—4號線地質條件的統計分析指出，南昌地區為典型上軟下硬二元結構地層，復合地層斷面為上覆砂、下伏泥質粉砂巖。上覆砂層為強滲透性地層，最大滲透系數可達4.65×10-2cm/s，且黏聚力小，結構松散，土體強度較低，易受刀盤擾動發生塑性流砂現象，一般采用滿艙推進；下伏泥巖黏聚力較高，土體強度較大，自穩性較好，可采用無支撐敞開式推進，且隨著埋深的變化，泥巖復合比例也不盡相同。因此，當盾構在復合地層中掘進時，上下地層間較大的物理力學性質差異極易引發掌子面處土體失穩，誘發地表沉降，對周圍建(構)筑物安全產生隱患。南昌地區盾構隧道典型地層剖面如圖1所示。

上覆砂層由于顆粒級配不同，其內摩擦角存在顯著差異，內摩擦角隨著粒徑的增大而增大。需要指出的是，除細砂外，其余類型砂土黏聚力基本為0，原因是南昌地區細砂上部往往為高黏聚力的粉質黏土層，與細砂存在不同程度的復合，導致細砂層黏聚力存在較大范圍波動。南昌地鐵盾構區間土層常規參數如表1所示。

本文以南昌地區典型上軟下硬復合地層斷面為例，探討淺埋隧道中不同泥巖復合比例下掌子面極限支護力上限解變化規律及破壞模式以及不同埋深、巖土體參數對支護力上限解的影響。

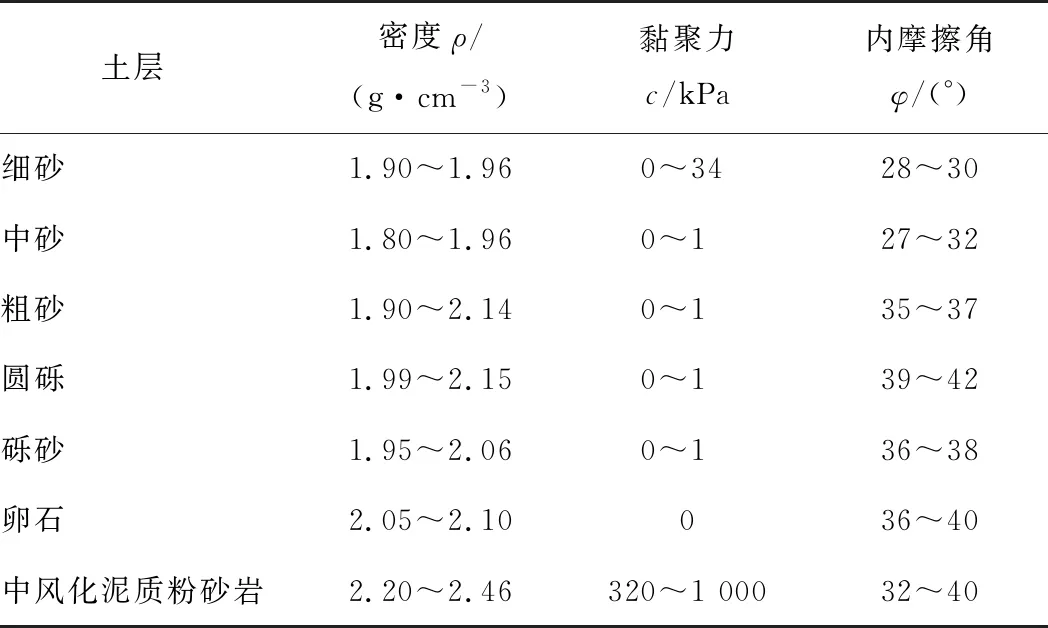
表1 南昌地鐵盾構區間土層常規參數統計

2 極限分析模型

2.1 極限分析理論

極限分析理論源自塑性力學中的剛塑性問題分析。該方法可避開傳統有限元彈塑性迭代求解過程，直接解得極限狀態下極限荷載分布與速度場，極大地減小求解難度，縮短求解時間。極限分析分為上限解與下限解，2類解的不同之處在于上限解為滿足位移邊界條件下的求解值，而下限解為滿足應力邊界條件下的求解值。其中，上限定理認為根據巖土體破壞的充分條件，可求解極限荷載的上限值，得到無窮多組上限解，但實際上結構在極限狀態下已經破壞，因此選取最小上限解作為極限荷載，該值為最接近實際的極限荷載[12]。

圖2示出由表面基礎試驗測得的塑性破壞現象及極限荷載位移曲線。如圖所示，荷載位移曲線包括彈性、彈塑性、塑性及土體強化或幾何變形導致的土體工作強化階段，其中荷載再次增加段(稱之為強化階段)是由于土體工作強化，或者是由于幾何改變所引起的基礎承載的強化段，應力可超出初始屈服面。假定土體為理想塑性介質并忽略幾何變形，隨著位移趨于無窮大，荷載仍為常數不變，由此解得的荷載即為塑性極限荷載，對于大變形或物理塑性破壞荷載適用性表現良好[13]。

2.2 模型的建立與參數取值

本文采用三維有限單元巖土極限分析軟件Optum G3對淺埋隧道中不同泥巖復合比例下掌子面極限支護力上限解進行分析。該軟件內置的極限分析模塊可通過上、下限混合極限分析法快速得到極限狀態下掌子面臨界支護壓力上限值，計算效率高于傳統有限元軟件，且可避免有限元或有限差分方法中通過尋找支護壓力-開挖面位移曲線的拐點來確定臨界支護壓力的不確定性。

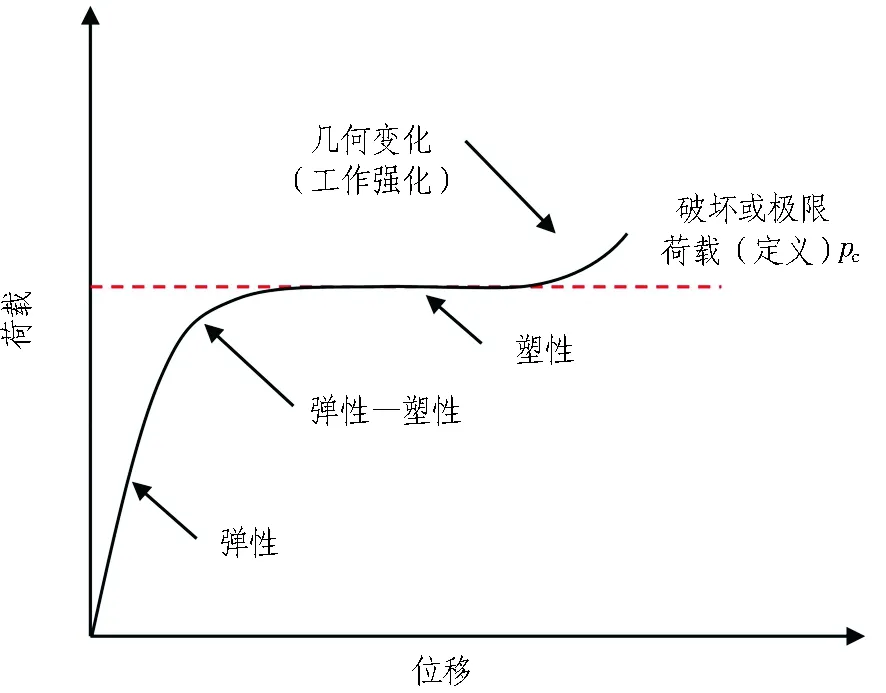
圖2 典型塑性破壞現象及極限荷載定義[13]

如圖3所示，建立Optum G3三維極限分析模型。由于盾構隧道開挖模型在隧道軸線方向上具有對稱性，為提升計算效率，只取隧道半邊進行研究。隧道直徑D=6 m，一次性開挖土體至9 m位置，對隧道四周側壁施加徑向約束，限制其徑向位移。綜合已有研究對模型尺寸的定義[14-17]，為消除邊界條件影響，模型長邊方向為3D，短邊方向為2D，隧道拱底與模型下表面距離為0.5D。模型上表面設置為自由，下表面限制水平及豎向位移，側面限制水平位移，采用自適應4節點四面體單元進行網格劃分，單元數量取10 000個，迭代次數為3次，選用混合求解器進行迭代求解。土體破壞服從Mohr-Coulomb屈服準則，上覆礫砂，下伏泥質粉砂巖，參數選取如表2所示，數據來源于南昌地鐵4號線地勘報告。

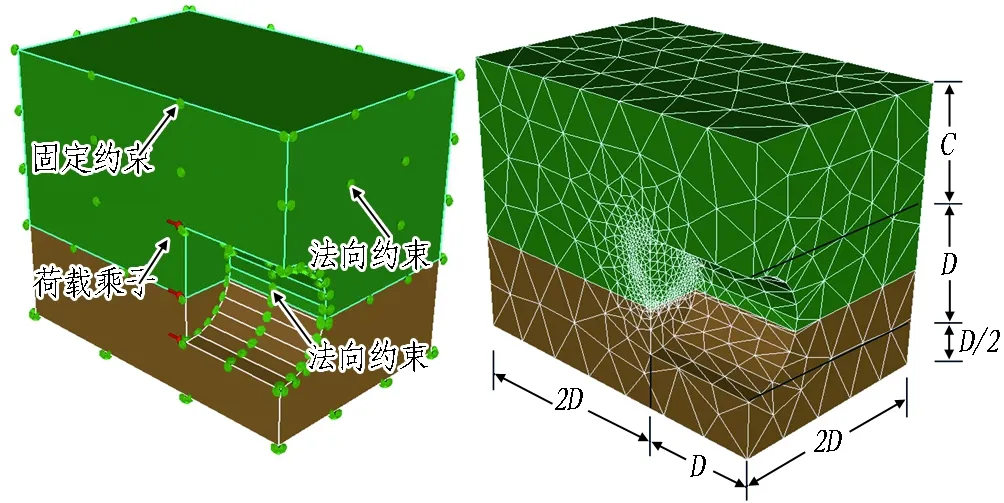
圖3 Optum G3三維極限分析模型

表2 土體物理力學參數

2.3 模型驗證

已有學者[16-18]利用理論模型和數值模型，計算了復合地層中掌子面支護壓力下限解，本文通過Optum G3建立復合地層中同工況下的三維極限分析模型，驗證模型的有效性。一次性開挖隧道至9 m處，凍結內部土體單元，對側壁施加法向約束以模擬襯砌對土體支撐作用，掌子面施加荷載乘子模擬均布支護壓力，隧道直徑D=6 m。

圖4(a)示出上、下土層分布關系，隧道中心線位于兩土層交界處，保持下層土體參數不變，通過改變上層土內摩擦角來反映掌子面極限支護力變化情況。圖4(b)示出不同內摩擦角下極限支護壓力下限值變化曲線。當下層土參數一定時，隨著上層土內摩擦角的增加，極限支護壓力下限值不斷減小，模擬結果的曲線走勢與前人研究結論基本一致，吻合較好，表明所建模型準確可靠。

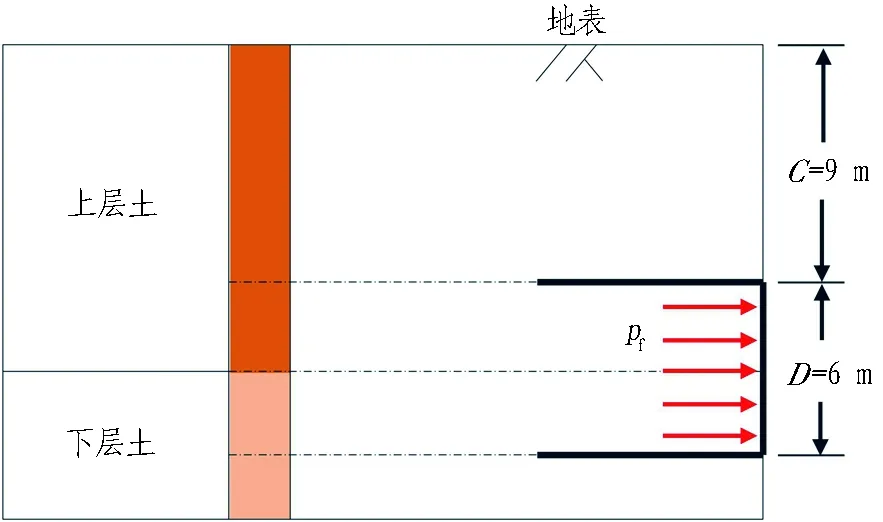
(a) 驗證模型土層相對位置關系

(b) 上層土不同內摩擦角下極限支護力下限值變化

3 參數分析

3.1 不同復合程度影響分析

盾構在復合地層中掘進時，由于掌子面不同類型巖土體的物理力學性質差異極大，伴隨著不同類巖土體復合比的變化，將顯著影響開挖斷面壓力分布。本節分別探討了復合地層中全斷面礫砂，巖砂比為0.25、0.5、0.75，全斷面泥巖這5類情況下掌子面極限支護力上限解的變化規律。

3.1.1 對支護力的影響

隨著掌子面泥巖占比逐漸提高，支護力上限值不斷增大，如圖5所示。當泥巖占比小于0.5時，變化較為平緩；當大于這一值后，支護力上限值迅速增大。表明在泥巖比例未超過一半時，同一埋深下，掌子面支護壓力主要受礫砂控制，礫砂黏聚力接近于0，掌子面處土體強度變化微弱，因此支護力上限值幾乎不隨泥巖比例的增多而變化；但當泥巖比例超過0.5后，由于泥巖黏聚力較大，隨著泥巖比例的升高，土體強度增幅較大，導致支護力上限值迅速上升。此外，全斷面泥巖對應支護力上限解為p1=5 057 kPa，全斷面礫砂對應支護力上限解為p0=2 397 kPa，兩者差異巨大，p1是p0的2倍多，表明當盾構從全斷面礫砂進入全斷面泥巖后，巖土體自穩性明顯變好，安全性明顯提高，實際施工中可適當減小土艙壓力以提高掘進速度。

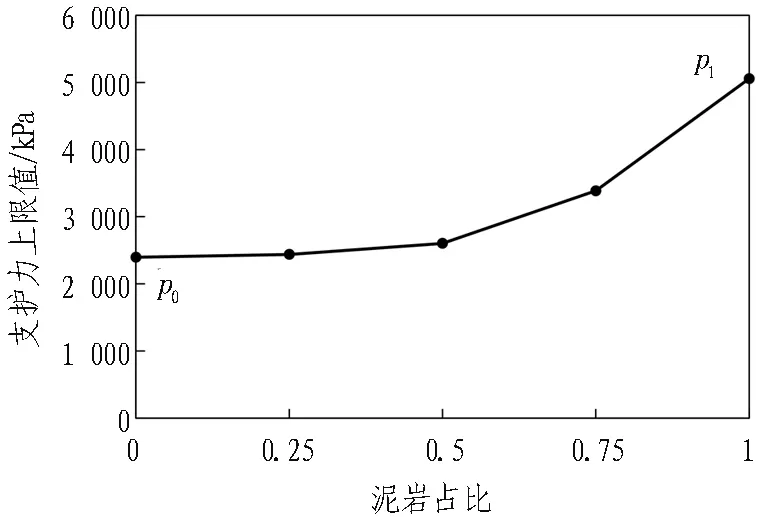
圖5 不同泥巖占比對上限支護力的影響

3.1.2 對失穩面的影響

剪切耗散是反映塑性變形強度的指標，圖6(a)—(f)展示了復合地層中泥巖占比0到1再到泥巖超拱頂3 m變化過程中，掌子面剪切耗散云圖的變化特征。由圖可知： 1)當掌子面極限支護力達到上限值時發生被動破壞，地表在貫通的失穩面頂部產生向上隆起，隆起范圍與失穩面縱向最大長度保持一致，且掌子面含有礫砂時，發生失穩地層均只在礫砂層，形成局部破壞模式； 2)當地層條件為全斷面砂層時，掌子面破壞點首先出現在拱底部位，自下而上形成漏斗狀破壞面延伸至地表，導致地面發生隆起； 3)隨著地層中泥巖比例的逐漸增大，砂層比例逐漸減小，復合地層的總體黏聚力不斷上升，掌子面破壞位置也從拱底向上移動。

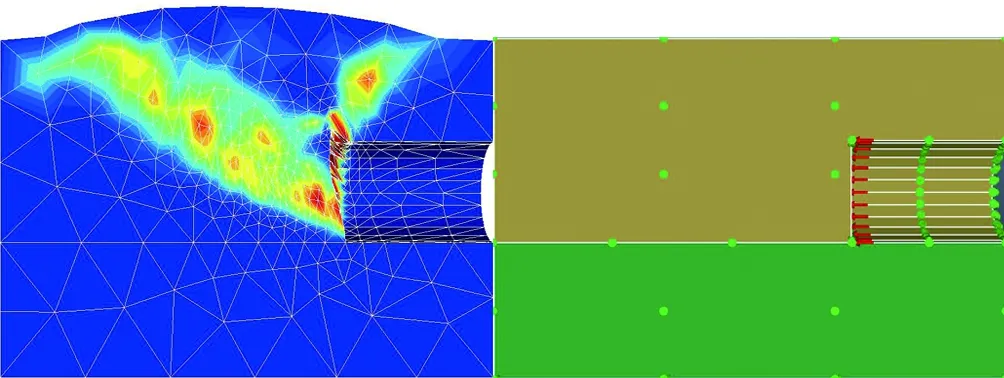
(a) 泥巖占0%

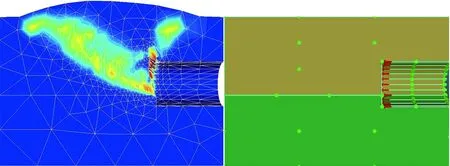
(b) 泥巖占25%

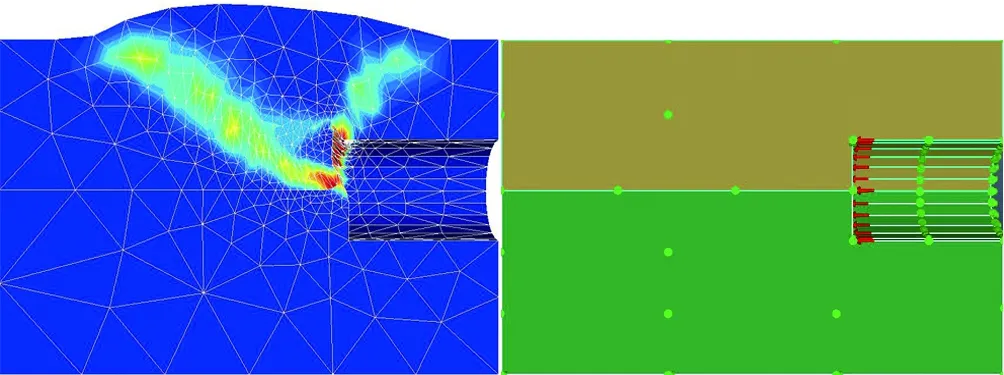
(c) 泥巖占50%

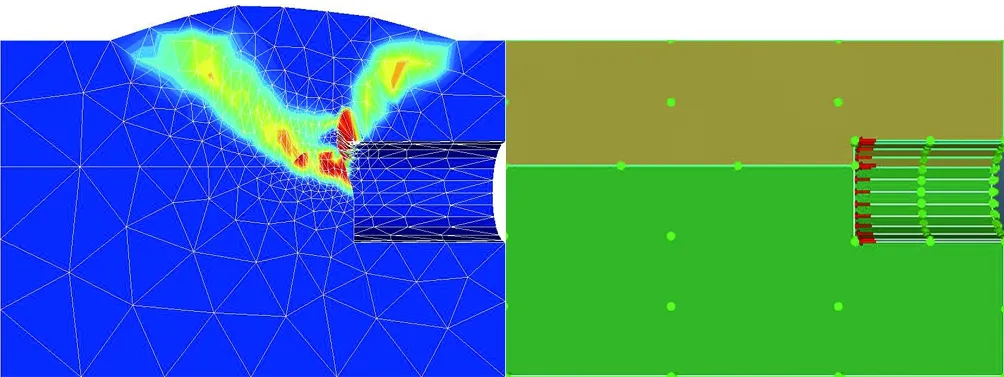
(d) 泥巖占75%

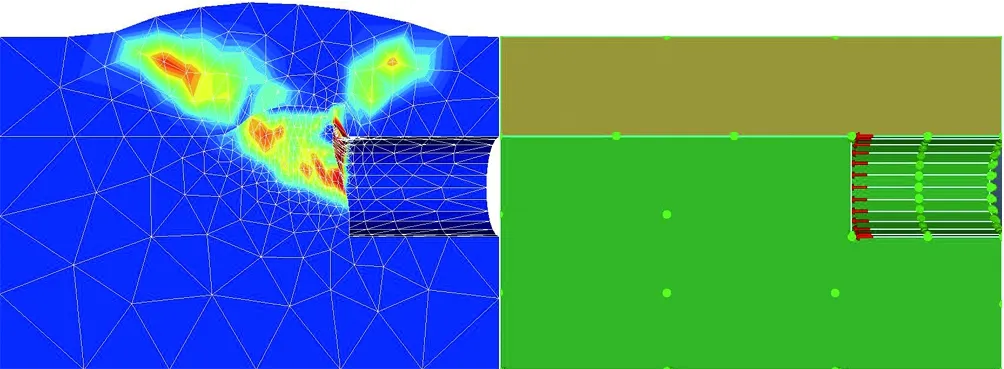
(e) 泥巖占100%

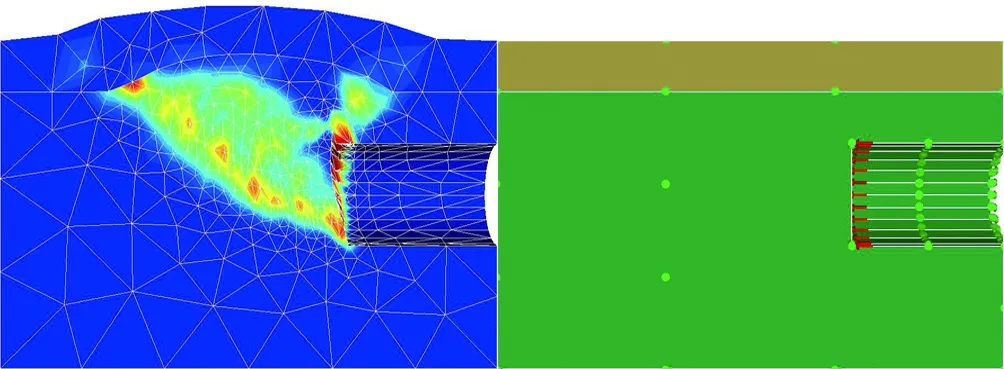
(f) 地層交界面位于拱頂3 m處

當泥巖占比小于0.5時，掌子面失穩破壞點基本發生在砂層與泥巖交界線處； 而當泥巖占比大于0.5后，掌子面失穩破壞點向拱底位置移動； 當地層交界線位于拱頂3 m處時，發生整體失穩。總體來看，當泥巖占比小于0.5時，掌子面最易失穩點位于砂層底部，此時破壞點位置主要受砂層控制； 當泥巖占比大于0.5時，掌子面易失穩破壞點出現在隧道中軸線以下，受泥巖控制。

3.2 不同參數影響分析

隧道埋深比、土體黏聚力、內摩擦角的改變將顯著影響掌子面極限支護力[2-3]。為探究這些參數變化對不同泥巖比例下上限支護力的影響，設計了3組參數分析模型，如圖7所示。第1組控制覆土c、φ值相同，探究埋深比C/D=0.25、0.5、0.75、1時不同泥巖比例下支護力上限解變化；第2組控制覆土埋深C、φ值相同，探究覆土黏聚力c=1、10、20、30 kPa對不同泥巖比例下支護力上限解的影響；第3組控制埋深C和覆土黏聚力c相同，探究內摩擦角φ=25°、30°、35°、40°時，對不同泥巖比例下支護力上限解的影響。

(a) (b) (c)

3.2.1 埋深比影響分析

盾構掘進過程中，泥巖比例的改變往往伴隨著埋深的變化，本節探究不同埋深比下，泥巖比例的變化對上限支護力影響，其余參數均保持不變。如圖8所示，極限支護壓力隨著埋深比的增加不斷升高，且埋深越大，增長的幅度越大。當C/D=0.25時，隨著泥巖占比不斷提高至0.75之前，極限支護力基本保持穩定，但當超過0.75后，極限支護力迅速上升；隨著埋深的增加，泥巖占比對極限支護力的敏感性顯著上升 ，當C/D=1時，極限支護力只在泥巖占比小于0.25時基本保持穩定，但超過0.25后便快速增長，且隨著泥巖占比的上升，極限支護力增長的速度不斷加快，斜率顯著增大。

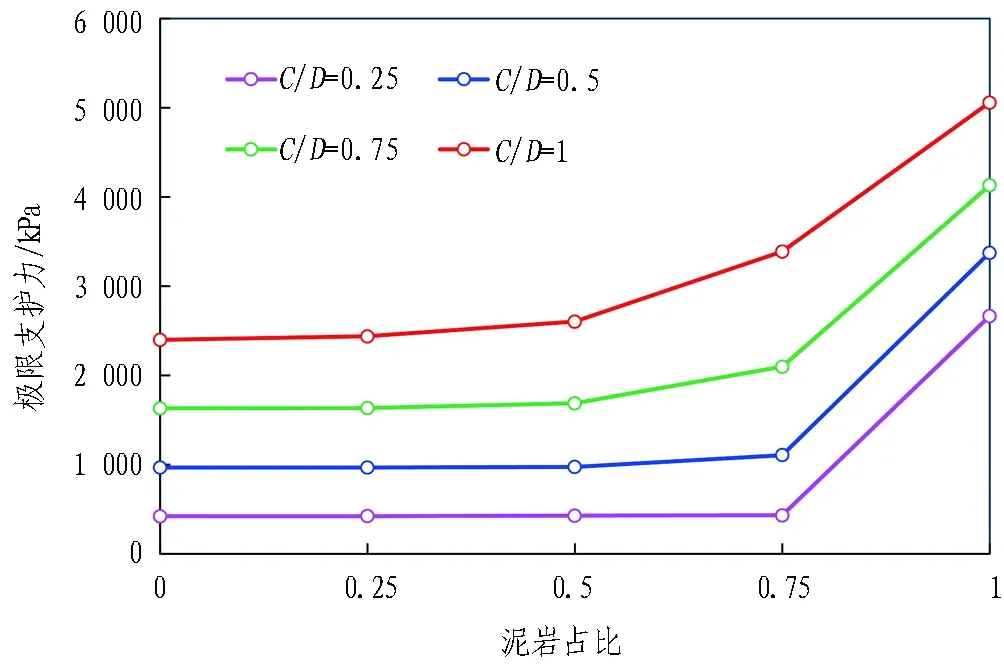
圖8 不同埋深比下泥巖比例對極限支護力的影響

利用MATLAB三維曲線擬合工具CFTOOL對不同埋深下，泥巖比例對上限支護力影響進行分析。自變量x、y分別為泥巖占比、埋深比C/D，應變量z為極限支護力，選擇Polynomial函數。為方便工程計算應用，同時保證計算精度，多項式自變量最高次項擬定為3次，擬合結果曲面如圖9所示，殘差R2為0.99，數據點均布于曲面附近，得到簡化計算方法如式(1)所示。

f(x,y)=66.9+946.3x+1 472y-7 815x2+

1 157xy+493.7y2+8 910x3-915.9x2y+

553.8xy2+305.5y3。

(1)

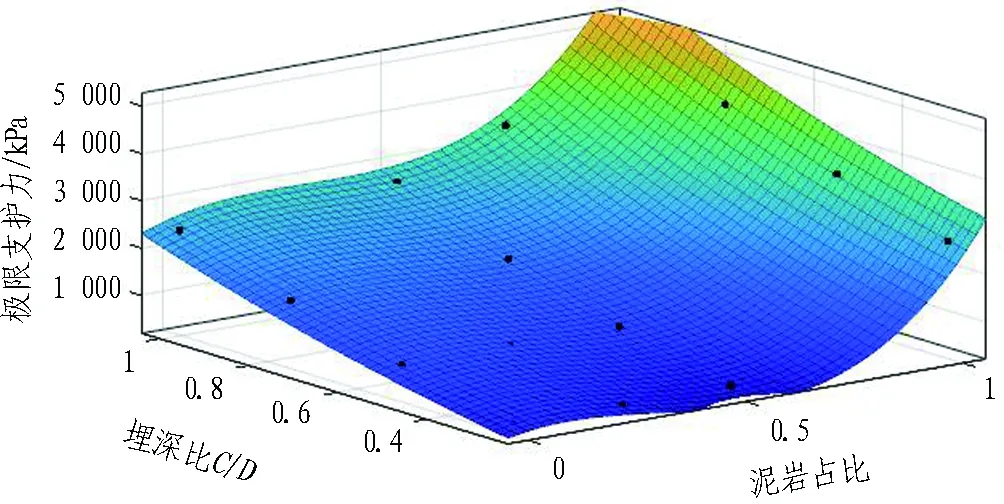
圖9 埋深比影響擬合曲面

為驗證計算公式的正確性，取上覆土c=1 kPa，φ=25°時，C/D=0.6、0.9的情況下極限支護壓力上限解與模擬結果作對比，結果如圖10所示。由圖可知，曲線走勢基本一致，擬合結果良好。

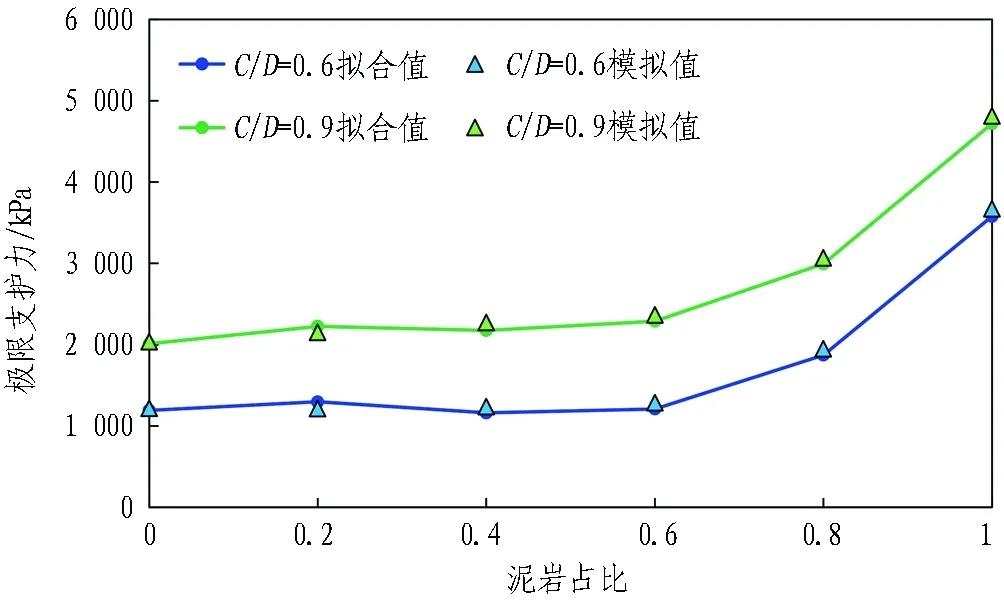
圖10 埋深比影響下極限支護力計算方法驗證

3.2.2 內摩擦角影響分析

復合地層掘進過程中，伴隨著泥巖比例的改變，還會出現多種砂層變化交匯的情況，土體的內摩擦角也會發生顯著改變。針對這類復雜的地質條件，有必要研究不同土體物理力學參數對極限支護力上限解的變化。

不同砂土的內摩擦角會隨著粒徑發生變化，粒徑越大，摩擦角也越大，因此本節探究不同內摩擦角下，泥巖比例的變化對上限支護力的影響。如圖11所示，不論在何種泥巖占比情況下，極限支護力均隨著內摩擦角的增大而增大，且當泥巖比例超過75%后，內摩擦角對極限支護力的影響變得微弱，主要原因是隨著泥巖比例的升高，砂土含量不斷降低，此時極限支護力主要取決于占掌子面比例較高的泥巖。總體來看，極限支護力仍然隨著泥巖占比的提高而不斷提升，直至進入全斷面泥巖地層后，極限支護力值趨于一致。

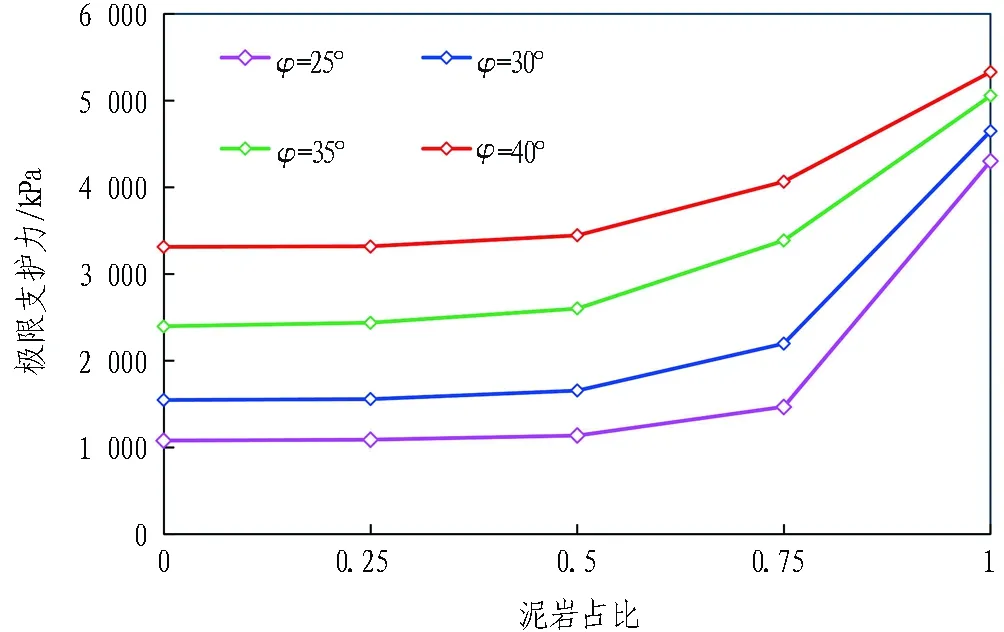
圖11 不同內摩擦角下泥巖比例對極限支護力的影響

利用MATLAB三維曲線擬合工具CFTOOL分析不同內摩擦角下，泥巖比例對上限支護力的影響。x、y分別為泥巖占比、內摩擦角φ，z為極限支護力，其余同上節。擬合結果如圖12所示，殘差R2為0.99，得到簡化計算方法如式(2)所示。

f(x,y)=2 361-444.3x+58.4y+357.1x2+

21.8xy-y2+2 710x3-31.5x2y+0.1xy2+0.015y3。

(2)

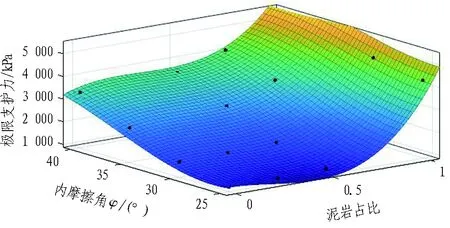
圖12 內摩擦角影響擬合曲面

計算公式驗證過程同上，取埋深比C/D=1，上覆土c=1 kPa時，φ=28°、38°情況下極限支護壓力上限解與模擬結果作對比，結果如圖13所示。由圖可知，曲線擬合良好，驗證了計算公式的正確性。

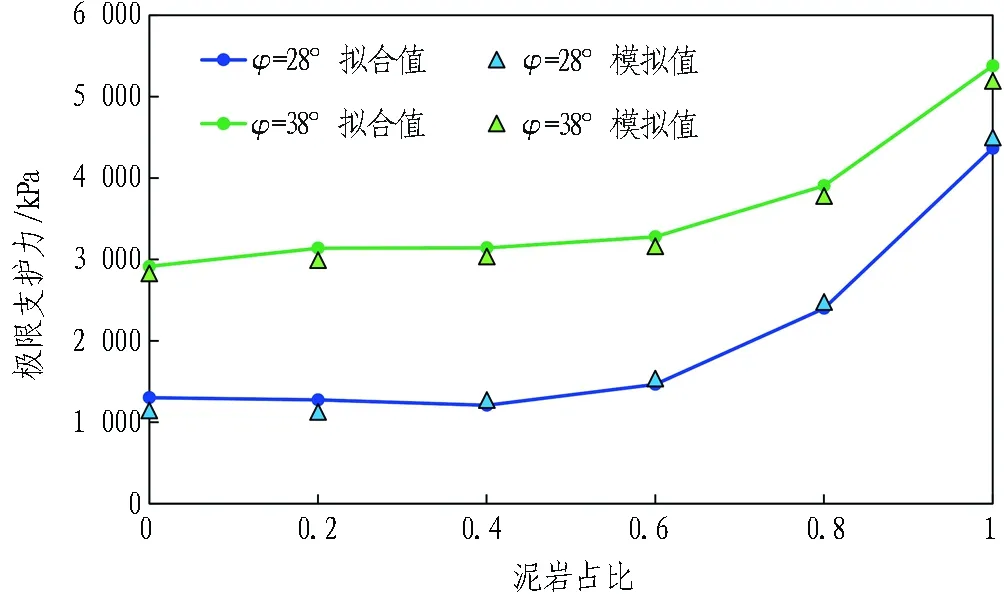
圖13 內摩擦角影響下極限支護力計算方法驗證

3.2.3 黏聚力影響分析

盾構在砂層-泥質粉砂巖復合地層掘進過程中，上覆于砂土之上的黏土層往往會與砂層交匯，而黏土的黏聚力較大，當砂層中混有不同程度的黏土時，往往會導致砂層的黏聚力發生改變。本節針對南昌地區黏土與砂土交匯復合地層，探究不同黏聚力情況下，泥巖比例對上限支護壓力的影響。

如圖14所示，總的來看，隨著泥巖占比的不斷增大，同一黏聚力下掌子面極限支護力穩步上升； 隨著黏聚力的不斷增大，極限支護力基本符合線性上升規律，不同泥巖比例下高黏聚力與低黏聚力值對應的極限支護力差值基本保持恒定，特別是當泥巖比例小于75%且其他條件不變時，極限支護力大小基本取決于上覆土的黏聚力大小。

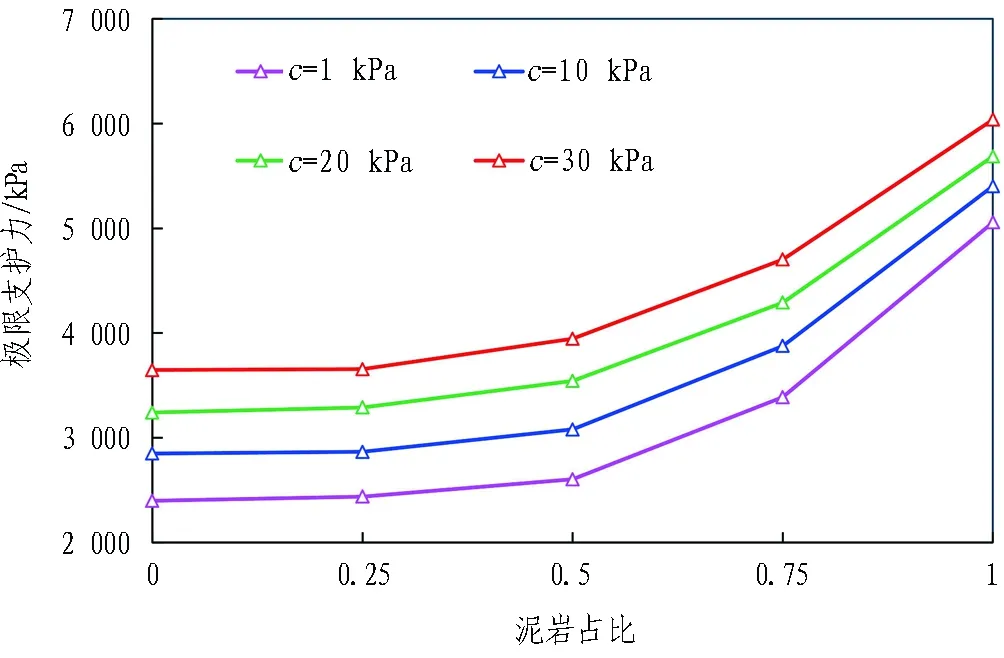
圖14 不同黏聚力下泥巖比例對極限支護力的影響

同3.2.2節利用CFTOOL工具繪制不同黏聚力下，泥巖比例對上限支護力影響圖，自變量x、y分別為泥巖占比、黏聚力c，應變量z為極限支護力，擬合結果如圖15所示。殘差R2為0.99，得到簡化計算方法如式(3)所示：

f(x,y)=23 880-10 710x-2 206y+1 622x2+

570.4xy+68.06y2+7 424x3-233.1x2y-

6xy2-0.65y3。

(3)

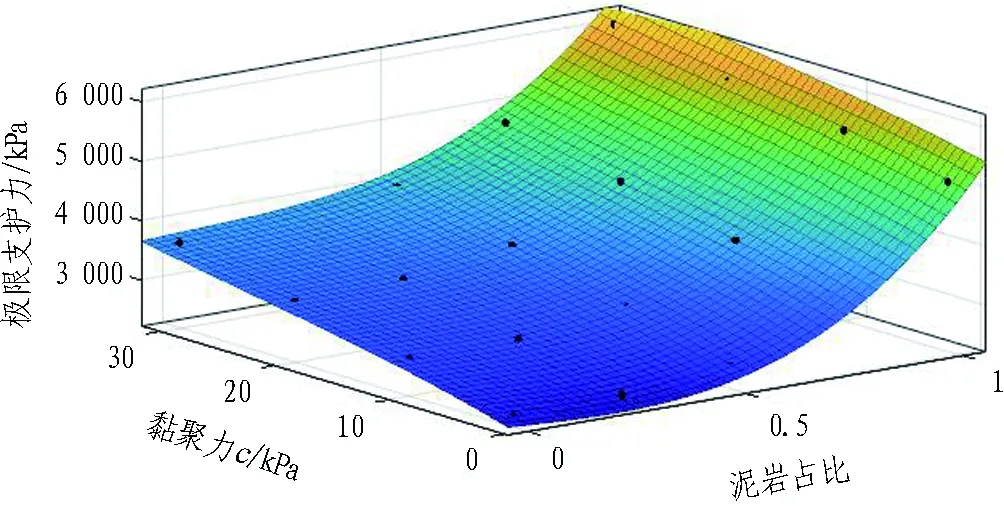
圖15 黏聚力影響擬合曲面

計算公式驗證同上，取上覆土C/D=1、φ=35°時，c=5、15 kPa情況下極限支護壓力上限解與模擬結果作對比，結果如圖16所示。由圖可知，曲線擬合良好，計算方法準確可靠。

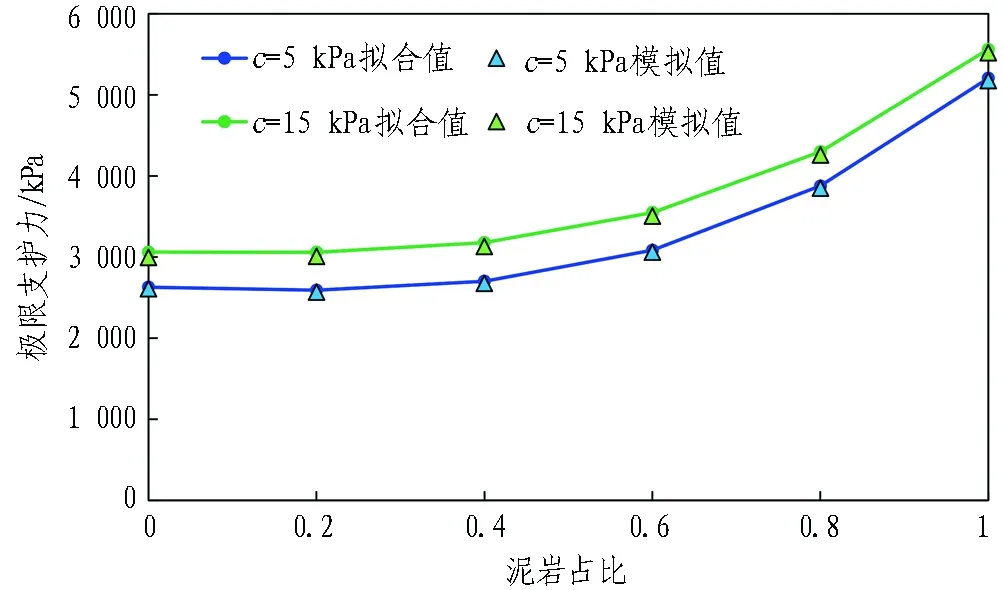
圖16 黏聚力影響下極限支護力計算方法驗證

4 結論與討論

本研究以南昌地區盾構開挖常見斷面“上覆砂層-下臥泥質粉砂巖”復合地層為例，通過Optum G3極限分析模型，探究了淺埋隧道中，不同泥巖比例下掌子面極限支護力上限解與破壞模式的變化情況。同時，分析隧道埋深比、內摩擦角及黏聚力的變化對極限支護力的影響，并擬合得到對應的計算公式，主要結論如下：

1)復合地層盾構隧道開挖過程中，隨著泥巖占比的不斷提高，掌子面極限支護力上限解不斷增大。當泥巖比例低于50%時，增長平緩，極限支護力取決于上覆砂土性質； 大于這一值后，支護壓力迅速上升，極限支護力取決于下部泥巖性質。

2)復合地層掌子面破壞模式顯著區別于均質土層，泥巖比例小于50%時，掌子面最易失穩點出現在砂層底部，即與泥巖交界面處。該點位置隨泥巖比例的增加而上升，當泥巖比例大于50%后，易失穩點出現在隧道中心位置，此時失穩點位置不再隨泥巖比例的上升而變化。

3)復合地層掌子面極限支護壓力隨著隧道埋深比、上覆砂土內摩擦角及黏聚力的增大不斷升高，且埋深越大，增長的幅度越大，當泥巖比例大于75%后，不同黏聚力下的極限支護力趨于接近。

目前，對于上下性質差異較大的復合地層中，掌子面破壞模式發展過程及最終可能發生的局部破壞效應研究較少，后續可針對失穩模式進一步開展機制性研究，另本文暫未考慮地下水影響，可對地下水滲流影響下復合地層掌子面極限支護壓力進行研究。