基于PCBN模型盾構下穿既有隧道施工安全風險評價

曾鐵梅， 劉 茜， 馮宗寶， *， 陳虹宇， 吳賢國

(1. 武漢地鐵集團有限公司， 湖北 武漢 430040； 2. 華中科技大學土木與水利工程學院， 湖北 武漢 430074； 3. 新加坡南洋理工大學土木工程與環境學院， 新加坡 639798)

0 引言

盾構隧道下穿既有隧道施工過程中極易誘發鄰近既有隧道的變形，對盾構下穿既有隧道施工風險開展實時的安全評估與控制具有重要的工程意義。目前，國內外對于盾構下穿隧道的施工安全研究主要集中于數值模擬和模型試驗等[1-2]。Khabbaz等[3]通過建立隧道施工與樁基相互作用的有限元模型,研究了在悉尼馬丁廣場下進行隧道施工的風險。Jallow等[4]利用PLAXIS 3D軟件對臺北捷運系統中某盾構隧道施工進行了有限元分析，探討了盾構施工中引起隧道長期沉降的機制。何夢超等[5]基于模糊故障樹模型，定量評估了地鐵盾構隧道下穿既有軌道的風險大小。阿卜杜拉等[6]通過模型試驗，針對既有隧道的應力變化，研究了盾構下穿對既有隧道的影響。王堅[7]結合理論分析和有限元數值仿真，研究了新建隧道盾構下穿既有隧道工程的影響。楊建烽等[8]通過模擬計算對盾構下穿既有地鐵區間隧道的沉降控制進行了研究。張毫毫等[9]對新建隧道下穿施工對既有上臥盾構隧道擾動影響規律進行了研究。上述研究主要針對盾構下穿既有隧道施工的沉降變形進行分析，而很少從風險評估角度進行系統的安全評價與預警研究，且傳統的評價方法沒有考慮到盾構施工過程中風險的復雜性和模糊性，也難以反映多源因素間的相互作用。

本文將貝葉斯網絡與Pair-Copula理論相結合，基于二者的優勢提出基于PCBN模型的盾構下穿既有隧道施工風險評價方法，考慮多源風險因素之間復雜的相關關系，得到更加準確的風險評價模型，通過建立的PCBN模型進行風險分析及定性和定量相關性分析，實現工程施工風險的實時評估和關鍵的安全控制因素識別，為工程安全管理提供決策支持。

1 方法及原理

1.1 Pair-Copula理論

Copula理論是在Sklar定理的基礎上發展而來的，能夠對所選取隨機變量之間的相關性進行描述，也稱相依函數[10]，其基本原理是采用某種映射將邊緣分布函數聯合成聯合分布函數[11]。若f(x1,x2,…,xn)為節點X=(X1,X2,…,Xn)的聯合分布密度函數，則在Copula函數的概念下，f(x1,x2,…,xn)可以被表示為：

f(x1,x2,…,xn)=f(x1)·f(x2|x1)·…·f(xn|x1,…,xn-1)。

(1)

在此思路下，將變量的各個邊緣條件概率密度函數的Pair-Copula密度函數相乘便可得到變量的多元聯合分布密度函數，具體思路為：

f(u|v)=Cuvj| v-j(F(u|vj),F(vj|v-j))·f(u|v-j)。

(2)

式中：v=(v1,…,vj,…,vd)為變量向量，其維度為d；vj(1≤j≤d)為從v中隨意抽取的向量；將不包括vj的v定義為v-j，v-j=(v1,…,vj-1,vj+1，…,vd)；Cuvj| v-j為Pair-Copula密度函數。

在此定義下，利用密度函數對分布函數進行還原，則有：

(3)

1.2 貝葉斯網絡

貝葉斯網絡通過有向無環圖來反映具體問題中復雜變量之間的連接關系，是一種基于概率理論的網絡模型，具有強大的不確定知識表達和推理能力[12]。對于貝葉斯網絡中任意隨機變量X=(xt1,xt2,…,xtn)，相應的聯合概率分布可以表示為：

(4)

式中：Xpa(tj)為隨機變量X在時期tj的父結點集合；T為時期長度。

如果隨機變量X為時間序列，且xti的父結點為(xtj-1,…,xt1)，則式(4)可以轉化為：

(5)

1.3 Pair-Copula貝葉斯(PCBN)模型

Kurowicka等[13]通過結合貝葉斯理論和Pair-Copula函數，引入了Pair-Copula Bayesian network這種改良的貝葉斯網絡，并擴展了Copula理論的應用范圍。令D=(V,E)表示一個BN對應的DAG，用Dm表示D的道德圖，P為Rd的絕對連續概率測度，此概念下有D=|V|。在所有概率分布符合P特征的變量中，任意取一個變量X，假設P的概率密度函數為f，且P中的所有變量的邊緣分布為F1,F2,…,Fd，基于上文所提到的Sklar定理可知，f可由F1,F2,…,Fd與相應的Copula函數C相乘來表示。

Bauer等通過研究與推理，發現C可由條件化下的許多Pair-Copula函數Cv,w|pa(v)來表示，在此概念中，v∈V，w∈pa(v)[14]。基于這個思路，貝葉斯概念下的網絡結構D中的每個相關節點的箭線w→v都擁有一個條件化下的Pair-Copula，則f可表示成：

(Fv|pa(v;w)(xv|xpa(v;w)),Fw|pa(v;w)(xw|xpa(v;w)))。

(6)

式中x=(xv)v∈V∈Rd。

這種基于Pair-Copula函數的貝葉斯網絡稱為PCBN模型。

2 基于PCBN模型的施工風險評價

本文提出一種將貝葉斯網絡和Pair-Copula函數相結合的盾構下穿既有隧道施工風險評價方法，對盾構下穿既有隧道進行實時有效的安全風險評估并為其提供決策支持，其評價流程如圖1所示。

圖1 基于PCBN模型的盾構隧道下穿既有隧道施工風險評價流程

2.1 評價指標體系建立

通過工程實踐和相關文獻分析，提煉出盾構下穿既有隧道安全風險的主要影響因素，包括隧道相關參數、土體條件、既有隧道條件、施工與管理因素4類，從而構建盾構下穿既有隧道安全評價指標體系[15]。

1)隧道相關參數： 新建隧道相關參數的設計是盾構隧道影響周圍土體和構筑物非常重要的一類因素，它可以反映隧道開挖的大致情況。新建隧道相關參數一般主要考慮新建隧道的直徑(X1)、兩隧道的凈距(X2)和兩隧道的平面夾角(X3)3個參數[16-17]。

2)土體條件： 土體作為新建隧道與既有隧道相互作用的中間媒介，土體條件對于盾構隧道下穿引起既有隧道的變形破壞有著至關重要的作用[18]。其中，壓縮模量(X4)、黏聚力(X5)、內摩擦角(X6)和泊松比(X7)是表征土體性質的幾個常見影響因素。

3)既有隧道條件： 既有隧道的變形破壞與自身現有的條件有很大關系，既有隧道的埋深(X8)、既有隧道的直徑(X9)和覆跨比(X10)會影響既有隧道的基底應力變化，從而影響隧道的變形[19]。既有隧道的健康狀態(X11)則在一定程度上決定了隧道承受變形的能力。

4)施工與管理因素： 盾構隧道施工階段，施工和管理因素對臨近既有隧道安全的影響則主要體現在對盾構施工參數合理性的控制上[20]。具體來說，盾構施工參數主要包括注漿壓力(X12)、土艙壓力(X13)、推進力(X14)和推進速度(X15)等。

2.2 PCBN模型構建

2.2.1 最優邊緣分布識別

邊緣分布函數的作用是對變量的概率分布進行正確描述，其識別結果會直接影響風險評估的可靠性和準確性。本文選擇Weibull函數、 Exponential函數、Normal函數和Gamma函數4種常用Copula函數作為備選函數，通過AIC準則和BIC準則2種方式來確定PCBN模型中風險指標的最優邊緣分布函數，以保證風險指標分布函數選擇結果的科學性。最優邊緣分布函數即為使AIC值和BIC值最小時的分布，AIC準則和BIC準則的具體公式為：

(7)

(8)

(9)

式(7)—(9)中：x1i,x2i為2個隨機變量；c(u1i,u2i)為分布函數的估計值；N為風險指標實測值的維度；k為Copula參數的個數，本文k取1。

2.2.2 PCBN模型設計

首先，根據專家知識和大量工程實踐經驗，將具有相關關系的風險指標用有向箭頭連接，初步構建盾構隧道下穿既有隧道施工安全風險評價的有向無環圖(DAG圖)，如圖2所示；然后，基于實測數據計算具有相關關系的風險指標間的Spearman秩相關系數，見式(10)；最后，根據計算的Spearman秩相關系數進行獨立性檢驗，將相互獨立的節點之間的箭頭去除，從而對初步構建的DAG圖進行修改和完善，并將各風險指標的最優邊緣分布輸入構建的DAG圖中，從而構建盾構下穿既有隧道施工安全風險評價的PCBN模型。

(10)

式中：dk為2個變量之間的等級差，即本文中2個風險指標實測值的排序之差；z為等級差的個數，即風險指標實測值的維度。

圖2 初步DAG圖

2.2.3 PCBN模型驗證

為了保證PCBN模型的合理性，需要對模型的有效性進行驗證。本文采用K-S檢驗對PCBN模型中單節點的邊緣分布進行擬合優度檢驗，判斷觀測樣本值和假設分布之間的差值是否符合設定的置信區間。給定一組長度為n的升序排列的樣本數據為x( · )，則其K-S檢驗的統計量為：

T=sup|F*(x)-Fn(x)|。

(11)

式中：F*(x)和Fn(x)分別表示假設的分布函數和基于實測數據的分布函數； sup表示F*(x)和Fn(x)之間距離集的總和。

2.3 基于PCBN模型的風險分析

利用貝葉斯網絡的概率推理技術，通過聯合概率分布，可以直接推算出n個風險因素Xi(i=1,2,…,n)組合下風險事件T的發生概率，從而便于施工人員在事故發生前預判事故風險等級，以便及早采取控制措施。風險事件(即葉結點T)不同風險等級發生的概率可用P(T=t)(t=1,2,…,5)表示，其計算公式為：

P(T=t)=P(T=t|X1=x1,X2=x2,…,Xn=xn)×

P(X1=x1,X2=x2,…,Xn=xn)。

(12)

2.4 基于PCBN模型的指標相關性分析

PCBN模型可以進行參數相依性的準確識別和高精度重構，基于所構建的PCBN模型進行基于百分位蛛網圖[21]和相關系數的相關性分析，可以定性和定量地判斷風險系統中與盾構下穿既有隧道施工風險相關性較大的風險因素，即為關鍵風險因素，并依據相關性大小確定決策的優先權，明確盾構下穿既有隧道風險管理的重點管理環節與檢查點。

3 案例分析

3.1 工程概況

武漢市地鐵8號線一期工程總長16.7 km，共設有12個站點，中間貫穿了永清商務區、徐東商業區、街道口商業區等經濟帶，是連接長江兩岸的一條重要交通線路。8號線一期工程采用土壓平衡盾構施工，在宏圖大道站至塔子湖站區間內下穿地鐵3號線，與3號線在金銀潭大道和宏圖大道的路口相交，相交后沿宏圖大道并行約200 m。在該區段設置100個監測點，獲得100組監測數據，如表1所示。

表1 隧道相交區間段監測數據

3.2 PCBN模型構建

3.2.1 最優邊緣分布識別與檢驗

基于表1中15個風險指標的實測值，在歸一化處理后，根據式(7)—(9)進行最優邊緣分布函數識別，并根據式(11)對各風險指標識別擬合結果進行K-S檢驗。設定顯著水平α=0.05，若統計量P值大于顯著性水平0.05，則假定的邊緣分布擬合；反之，假定的邊緣分布不擬合。計算得到各指標最優邊緣分布K-S檢驗的擬合優度均較好。部分指標識別和檢驗結果如表2所示。

3.2.2 貝葉斯網絡結構設計

首先，將施工風險評價指標體系中的15個風險因子作為貝葉斯網絡DAG圖的節點，結合專家經驗和相關文獻資料，初步構建出風險評價的DAG圖。然后，根據式(10)進行獨立性假設檢驗，對初步DAG圖進行修剪和完善。設定顯著性水平為0.1，若P值大于0.1，則兩節點為獨立關系，否則兩節點間存在一定程度的相關關系。節點之間獨立性檢驗結果顯示X3和X2、X9和X8、X13和X12之間相互獨立，則剔除其經驗相關關系，修剪完善后的DAG圖見圖3。

表2 AIC和BIC準則的最優邊緣分布函數及擬合優度K-S檢驗結果

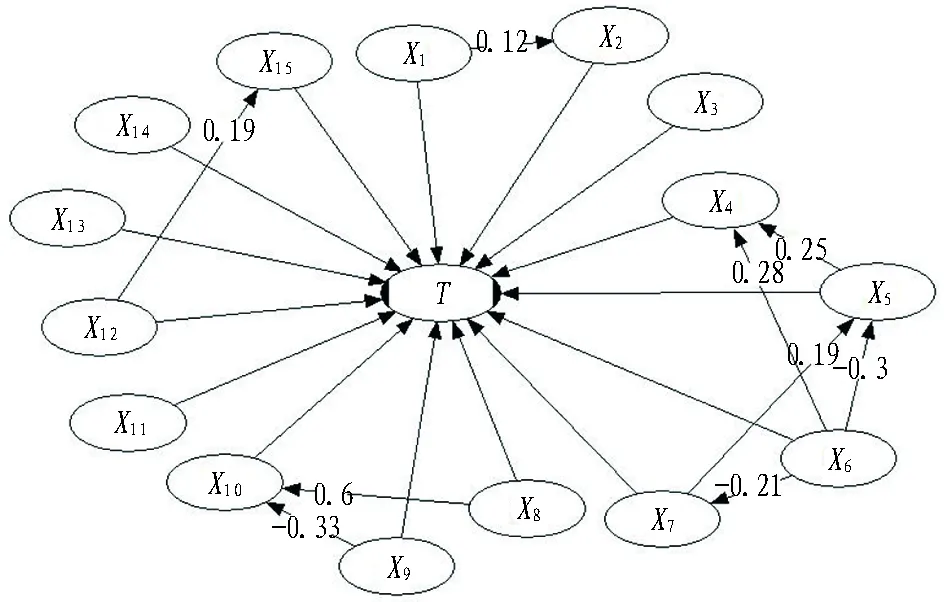
圖3 調整完善后的風險系統PCBN網絡DAG設計圖

3.3 基于PCBN模型的風險分析

基于構建的PCBN模型，結合工程實際與專家經驗，可將該工程的安全風險劃分為5個安全狀態，對應5個風險等級，各個風險等級與工程風險區間值的對應關系如表3所示。

表3 工程風險等級標準

根據式(12)，通過各節點的分布參數及各個節點之間的相關系數進行風險值推理，得到盾構下穿既有隧道施工風險值，繪制出該工程盾構下穿既有隧道施工風險評價的PCBN模型，如圖4所示。

圖4 盾構隧道下穿既有隧道施工風險PCBN模型圖

由圖4可知，該工程施工過程的風險值均值計算結果E(T)=0.387，標準差計算結果為0.071 9，故該工程施工風險值范圍為[0.315 1,0.458 9]。依據表3可以判斷該工程盾構下穿既有隧道施工風險等級為Ⅲ級，即該工程施工風險狀態為基本安全。但是，由于在Ⅲ級風險值范圍內，該工程的風險值偏高，有向Ⅳ級較危險狀態發展的趨勢，因此，可以判斷某些監測點或者該隧道的某些風險指標的風險等級狀態較高。為了對盾構下穿既有隧道施工風險進行管理與控制，應當進一步確定關鍵致險因子。

3.4 基于PCBN模型的指標相關性分析

基于PCBN模型進行定性和定量的相關性分析，確定相關性大的因素為關鍵致險因子，為盾構下穿既有隧道施工風險控制提供依據。

3.4.1 百分位蛛網圖分析

百分位蛛網圖通過多個樣本有效反映了PCBN模型中各個風險指標與施工風險之間取值的相關關系，通過條件化蛛網圖，即設定施工風險值的取值區間，即可觀察條件化下各個風險指標的取值情況，從而定性地確定風險系統中與工程施工風險變化相關性較大的風險指標。圖5為盾構下穿既有隧道條件化的風險蛛網圖。由圖可以看出，在T高概率值和低概率值的條件化下，指標X12、X14、X15的藍色樣本線條(T的高概率值)分布基本集中于縱軸上部，黑色樣本線條(T的低概率值)基本集中于縱軸下部。這表明，在該工程風險系統中，指標X12、X14、X15與風險變量T的高概率值和低概率值具有較強的相關關系，這3個因素對風險變量T的風險等級的影響更大。故注漿壓力(X12)、推進力(X14)、推進速度(X15)為影響本工程施工風險的重要指標，當盾構隧道下穿既有隧道施工過程的風險較高時，應首先對這3個風險指標采取控制措施。

圖5 盾構隧道下穿既有隧道條件化的風險蛛網圖

3.4.2 相關系數分析

相關系數能夠定量反映致險因子與施工風險之間的相關程度，從而判斷對施工風險影響較大的關鍵因素。本文選用Pearson相關系數和Spearman相關系數分別度量Xi與T之間的線性和非線性相關關系。一般相關系數大于0.5時認為具有顯著相關性，當相關系數為0.3～0.5時，認為具有中等相關性。基于構建的PCBN模型，計算15個風險指標關于工程施工風險T的Pearson相關系數和Spearman相關系數，結果如圖6所示。

圖6 指標Xi關于施工風險T的相關系數

由圖6可知，在風險系統的15個風險指標中，X15、X14、X123個指標的相關系數值最大。X15與工程施工風險的線性相關系數和非線性相關系數均大于0.5，表明X15與工程施工風險之間呈顯著相關；X14與工程施工風險的線性關系為顯著相關，非線性關系為中等相關；X12與工程施工風險的線性關系和非線性關系均為中等相關。因此，本工程中推進速度(X15)為對盾構下穿既有隧道施工風險影響最大的風險指標，推進力(X14)和注漿壓力(X12)為影響次之的2個風險指標，它們3個指標是本工程風險系統中的關鍵風險指標，該分析結果與通過蛛網圖定性分析所獲得的結論一致。根據所識別出的關鍵風險指標，可以采取一定的風險預控應對措施。在施工過程中，應當重視對主要因素X12、X14、X15的監測和檢查，當施工風險過高時，首先考慮推進速度、推進力和注漿壓力的參數是否在正常范圍，并對盾構推進系統、注漿系統進行檢查，及時進行檢修調控，從而降低工程施工風險。

4 結論與討論

本文在貝葉斯網絡的基礎上引入Pair-Copula理論，提出了一套基于PCBN模型的風險評價方法，在模型中通過不確定推理確定施工風險等級，又通過相關性分析識別關鍵致險因素，實現了盾構下穿既有隧道施工過程的安全風險評價。以武漢某隧道下穿工程為背景進行實例研究，主要結論與討論如下：

1)基于實測數據，利用提出的PCBN模型進行風險分析，確定該隧道工程的施工風險等級為Ⅲ級，施工風險狀態為基本安全，但有向較危險狀態發展的趨勢。

2)該工程施工風險系統中的關鍵風險指標為注漿壓力(X12)、推進力(X14)和推進速度(X15)，為盾構下穿既有隧道施工風險管理提供了依據。

3)本研究僅在二維空間下，利用PCBN模型對于兩兩節點之間的相關性進行了分析，在未來的工作中，可以研究3個及以上節點的相關性，探究多維空間下系統內部的相依性關系，實現更科學的決策與管理。